مرحبا عزيزي القارئ! أقدم إليكم ترجمة باللغة الإنجليزية لمقال "فيزياء ، الحدود التالية" للكريس هيكر.

واجهت أنا ، وهو مطور جافا مبتدئ ، حقيقة أن المواد اللازمة لإنشاء محرك في اللعبة تقدم باللغة الإنجليزية فقط ، وبالتالي تمت ترجمة هذه المقالة. سيكون هناك ثلاث مقالات أخرى في السلسلة ، سأقوم بنشرها في أقرب وقت ممكن. هل لديك قراءة لطيفة!

حدود جديدة في الفيزياء

ليس هناك شك في أن الرسومات في اللعبة تصبح أكثر واقعية كل عام. اليوم ، يقوم الجميع بإنشاء (أو على الأقل عرض لقطات) عوالم ثلاثية الأبعاد مع خرائط نسيج ، وعندما يجتمع عدد كاف من الأشخاص المجتهدين للعمل في مشروع واحد ، يمكن لكل مطور رسم مليارات من المضلعات من القوام والظلال الواقعية في الثانية. من الناحية الفنية ، ما الذي يجب عمله لإنشاء لعبة على مستوى عالٍ؟ هل سيكون بمقدور كل مطور لديه نسخة من كتاب "تعلم كيفية استخدام أجهزة ثلاثية الأبعاد في 21 يومًا" إنشاء لعبة رائعة حقًا؟

لا على الإطلاق. سيستمر المطورون الراقيون في رفع المستوى في العديد من التقنيات المختلفة (مثل تعقيد واجهة المستخدم الرسومية والذكاء الاصطناعي والشبكات). بالطبع ، كل هذا مهم للغاية ، لا يمكننا مناقشة أي منها بجدية دون تحديد التفاصيل. ومع ذلك ، هناك تقنية واحدة تنطبق على كل شيء ، والتي ، في رأيي ، ستصبح عاملاً حاسماً في المستقبل القريب: الفيزياء.

النظر في المثال التالي: هل تتذكر هذه التروس الغزل ضخمة في واحدة من المستويات المبكرة من Duke Nukem 3D؟



الشكل 1. لقطة شاشة من لعبة "Duke Nukem 3D"

فقط تخيل أن تناوبها لن يوصف بالرسوم المتحركة الدورية ، ولكن بواسطة محرك فعلي حقيقي. فجأة ، أصبحت التروس شيئًا أكثر من مجرد زخرفة للألعاب ، تمامًا كما ينحرف أحدهما عن زاوية معينة ، ويتدحرج في الممر خلفك ، كما في أفلام إنديانا جونز. أو تخيل أنه بعد إطلاق النار على أداة إطلاق من قاذفة صواريخ ، سوف يتدحرج الممر ويسحق صديقك ، الذي تسلل وراءه لقتلك! المحركات المادية تجعل مثل هذه الحالات حقيقية.

المحاكاة البدنية هي ما يجعل عالم اللعبة كله: بفضله ، "هنا" موجودة هنا ، إذا فهمت ما أقصده. أي سحر في الرسومات في العالم لن يسمح للاعب بالغطس في عملية اللعبة إذا كان يتداخل مع لاعب آخر ، أو في جدران المستوى ، أو إذا لم تشعر كتلة ولحظة الكتلة. وجد رسامو الرسوم المتحركة في ديزني أن شعور الجماهير هو ما يفصل الرسوم المتحركة الجيدة عن الرسوم المتحركة السيئة. وفقًا للكتاب الملحمي Disney Animation: The Illusion of Life لـ Frank Thomas و Ollie Johnston ، على رسامي الرسوم المتحركة من Disney ، حتى مجرد تعليق ملصق في الاستوديو ، أن يسألوا أنفسهم دائمًا: "هل هناك الكثير من الوزن والعمق والتوازن في رسمهم؟" ؟ "

ولكن اليوم تقريبا كل لعبة لديها محرك الفيزياء ، أليس كذلك؟ مما لا شك فيه ، هذا هو ما يمنع سيارتك من السقوط على حافة عالم اللعبة ، وذلك بفضل شخصياتك لا تطير إلى الفضاء عندما تقفز ، وهذا يلقي قاربك إلى الجانب عندما ينفجر صاروخ في مكان قريب. ومع ذلك ، فإن معظم المحركات المادية في الألعاب الحديثة ضعيفة للغاية. إنهم يتعاملون فقط مع مهمة منع السيارة من السقوط فوق حافة العالم ، لكن قدراتها لا تكفي لنقل اللعبة إلى مستوى جديد - حيث يمكن أن ينفجر حطام سيارة محطمة على المسار ، مما يؤدي إلى لفة الجدران وغيرها من السيارات.

تشمل الآثار الجسدية الأخرى التي يتم تجاهلها غالبًا: من تأثيرات التواء البسيطة نتيجة للإضراب المماسي ، إلى الشخصيات في اللعبة نفسها التي تحافظ على توازنها وتتحرك ، على عكس تلك الرسوم المتحركة الثابتة. أعتقد أن العديد من المطورين يتجاهلون هذه الاحتمالات لأنهم لا يفهمون الرياضيات التي تصف الفيزياء ، أو كانوا منشغلين جدًا في إنشاء خرائط نسيجية للتعرف عليها. سوف يهتم هجوم الأجهزة التي تعمل مع 3D بالأخير ، وأبدأ سلسلة جديدة من المقالات. المادة الأولى ستهتم بالشكليات. بنهاية دورتنا ، يمكنك أنت بنفسك إنشاء محرك مادي يجعل اللاعبين يشعرون بالغمر التام في اللعب ، وذلك بفضل الواقعية المذهلة ، أو السريالية المسلية ولكن المستمرة.

تحذير! الفيزياء = الرياضيات ، من أجل إكمال مشروع مثير للاهتمام ، سوف تضطر إلى استخدام كليهما. قبل أن يخيفك هذا ، اسمحوا لي أن أشير إلى أن الرياضيات التي تصف الفيزياء ليست فقط أنيقة وجميلة ، بل لها أيضًا شخصية مطبقة. وهذا هو ، أنها ليست الرياضيات المجردة للرياضيات. كل معادلة نستخدمها لها معنى مادي حقيقي. نقوم بإنشاء معادلات من نموذج مادي ، وفي المقابل تخبرنا المعادلات كيف يتصرف النموذج في الوقت المناسب.

المشاريع الكبرى

الفيزياء مجال علمي واسع. لكننا مهتمون حقًا بقسمها الصغير المسمى "ديناميات" ، أو بتعبير أدق ، "ديناميات المواد الصلبة". يمكن تعريف الديناميكيات من حيث القسم ذي الصلة - الحركية (عقيدة الحركة في الوقت المناسب). الكينماتيكا لا تركز على أسباب الحركة أو كيف انتهى الأمر بالهيئات حيث تصف الحركة. على العكس من ذلك ، تصف الديناميات القوى والجماهير التي تساهم في تغيير القيم من الحركية إلى الوقت. إلى أي مدى سوف تطير كرة البيسبول إذا كانت مدة الرحلة 10 ثوان وكانت سرعتها الأولية 50 كم / ساعة ، والمسار - خط مستقيم - يمثل مشكلة حركية ؛ إلى أي مدى سوف تطير كرة البيسبول في حقل الجاذبية على الأرض ، إذا ضربتها بمضرب - هذه مشكلة ديناميكية.

يتعلق جزء الديناميات التي تصف المواد الصلبة بالقيود التي نضيفها للكائنات المحاكاة. لا يتغير شكل الجسم الصلب أثناء المحاكاة - يكون الجسم على الأرجح خشبيًا أو معدنيًا أكثر منه شبيه بالهلام. يمكننا إنشاء أشكال مفصلية ، على سبيل المثال ، لشخص ما ، من خلال بناء كل جزء من الشكل من جسم صلب وخلق أربطة بينهما ، لكننا لن نعول على العظام التي تنحني تحت التوتر أو تأثيرات مشابهة. سيسمح لنا ذلك بتبسيط معادلاتنا دون فقد جودة السلوك الديناميكي المثير للاهتمام للهيئات.

على الرغم من أننا سننظر في هذا الجزء الصغير من الديناميات ، فإن ديناميكيات الجسم الصلب ستتطلب سلسلة من المقالات لشرح الجوهر. نبدأ رحلتنا من خلال دراسة أساسيات برمجة الكمبيوتر لوصف حركة جسم صلب الطائرة تحت تأثير القوات. أكرر بإصرار "برمجة الكمبيوتر" ، لأنه بالإضافة إلى المعادلات التي نكتبها للحركية والديناميكية ، سنتعلم أيضًا كيفية حل هذه المعادلات باستخدام العمليات الحسابية بأرقام الفاصلة العائمة ، وهو أمر حيوي يعرفه كل مبرمج. أقول "صلبة مسطحة" لأننا سنتعامل فقط مع العالم ثنائي الأبعاد خلال المقالة التالية وما بعدها. يمكن أيضًا نقل المبادئ - وفي الواقع أكثر من مجرد معادلات - إلى العالم ثلاثي الأبعاد ، ولكن بالتأكيد كل شيء أبسط بكثير في العالم ثنائي الأبعاد ، لذلك سوف ندرس هناك حتى نشعر بالثقة لدخول حيز ثلاثي الأبعاد. في المقالات المستقبلية ، سوف نتعلم وصف تأثير الدوران ، ومعالجة جهات الاتصال ، وبطبيعة الحال ، كيفية القيام بكل هذا في عالم ثلاثي الأبعاد. حسنا ، ما يكفي من الكلمات! لنبدأ!

العمل مع مشتق

قد يكون هذا بمثابة مفاجأة لك ، لكن لا يمكنك تحريك أي كائن بمجرد دفعه. أعلم أنك تعتقد أنني مخطئ في إثبات عكس ذلك بإلقاء هذه المجلة في سلة المهملات لكتابة مثل هذا الهراء ، لكن هذا صحيح! الضغط على المجلة فقط لن يؤثر بشكل مباشر على موقعها في الفضاء. في الواقع ، لا يؤثر الضغط بشكل مباشر على سرعته. ما يؤثر في الواقع هو تسارع المجلة ، وفي الواقع هو واحد من أهم الاستنتاجات في تاريخ العلوم.

من أجل استخدام هذه الحقيقة من أجل القيام بشيء مثير للاهتمام ، نحتاج أولاً إلى الحديث عن العلاقة بين موضع الجسم والسرعة والتسارع. في الواقع ، ترتبط كل هذه القيم ارتباطًا وثيقًا (كما تعلمون): السرعة هي مؤشر على التغيرات في إحداثيات الجسم مع مرور الوقت ، والتسارع هو مؤشر للتغيرات في السرعة. الأداة الأساسية لدراسة التغيرات في هذه الكميات بمرور الوقت هي التفاضل والتكامل. إذا فهمت هذا ، فإننا نمضي قدمًا. أفترض أنك جيد في الرياضيات. سنستخدم فقط الحسابات العددية والنواقل البسيطة (المشتقات والتكاملات) ، لكن لن يكون ذلك ضروريًا إذا كنت معتادًا على الرياضيات ككل. كمرجع: كتابي المفضل عن الحوسبة هو حساب التفاضل والتكامل مع الهندسة التحليلية لتوماس وفيني.

التنسيق والسرعة والتسارع هي حركيات سيتم مناقشتها في هذه المقالة. من الواضح أن موقع المادة الصلبة في عالم ثنائي الأبعاد هو زوجان من الإحداثيين X و Y ، يدلان على إحداثيات مساحة نقطة معينة من الجسم. مشتق متجه الإحداثيات هو متجه السرعة ، ويوضح لنا في أي اتجاه تتحرك النقطة (والجسم ، إذا تجاهلنا الدوران ، الذي يحدث الآن) ومدى سرعة تحركه. حساب التفاضل والتكامل المتجه هو مجرد حساب التفاضل والتكامل القياسي لكل عنصر من عناصر المتجه ، وبالتالي فإن مشتق إحداثي X هو سرعة الجسم بالنسبة إلى X ، وهكذا. نقدم الترميز التالي. دع إحداثي الجسم يكون المتجه r ، والسرعة هي المتجه v أو المتجه r مع الأعداد الأولية. نحصل على المعادلة:

$$

$${{dx} \ over {dt}} = v = r '$$

المعادلة 1

إذا قمنا بتمييز متجه السرعة فيما يتعلق بالوقت ، فسيوضح ذلك كيف يتغير متجه الإحداثيات مع الوقت. يتم تحديد التسارع عن طريق القياس. هذا هو المشتق الأول للسرعة أو المشتق الثاني لمتجه الإحداثيات:

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r '' = {{dr '} \ over {dt}} = {{dv} \ over {dt}} = v' = a$$

المعادلة 2

سوف يمنحنا تكامل التسارع السرعة ، ودمج التسارع مرتين ، نحصل على الإحداثيات.

تُظهر هذه العلاقات في علم الحركة أنه يمكننا العثور على تسارع الكائن ، ويمكننا دمجه بمرور الوقت للحصول على السرعة والتنسيق. كما سنرى لاحقًا ، سننتقل إلى التكامل عدة مرات في شفرة المحاكاة الخاصة بنا وسنحسب موضعًا جديدًا لدينا لكل إطار. الصيحة الرسوم المتحركة!

هنا مثال بسيط لعالم أحادي البعد يمكننا دمجه في التحليل. دعنا نوافق على أننا نريد العثور على التغيير الإحداثي من نهاية الإطار الأخير إلى وقت الإطار الحالي لرسم الموضع الحالي. بعد ذلك ، نقول أن تسارع المواد الصلبة لدينا كان مساوياً لـ 5 وحدات تعسفية / ثانية ^ 2. سنستخدم الوقت المنقضي من نهاية الإطار الأخير كمتغير t (في عنصر التكامل dt).

$$

$$v (t) = ∫adt = ∫5dt = 5t + C$$

المعادلة 3

تظهر المعادلات أعلاه أن السرعة هي وظيفة الوقت المنقضي من الإطار الأخير. وجدنا ثابت التكامل ، C ، والذي يساوي السرعة الأولية في بداية فترة التكامل (في t = 0).

$$

$$v (0) = 5 (0) + C$$

$$

$$v_0 = {C}$$

المعادلة 4

$$

$$v (t) = 5t + v_0 {}$$

الآن نقوم بدمج معادلة السرعة الخاصة بنا للعثور على الإحداثي (مرة أخرى ، لا تنسى أن ثابت التكامل):

$$

$$r (t) = ∫v (t) dt = ∫5t + v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

المعادلة 5

استنادًا إلى المعادلة 5 ، لا يمكننا إيجاد الموضع الحالي إلا من خلال تسريع معين إذا علمنا بالتنسيق الأولي والسرعة (التي سنتخذها من الإطار الأخير) والوقت المنقضي. متغير الإدخال هو الوقت ، وقيمة الوظيفة هي الموضع الحالي. سنشير أيضًا إلى الوقت في المعادلة 4 لحساب السرعة النهائية حتى نتمكن من استخدام هذا كشرط أولي للإطار التالي.

قد تكون القوة معك

الآن لدينا إدراك أننا نحتاج إلى ضبط التسارع بشكل صحيح لدمج معادلات الحركة من أجل الحصول على الرسوم المتحركة. إخراج مكبرات الصوت على خشبة المسرح. تذكر ، كما قلت ، بالضغط على شيء ما ، هل تؤثر بشكل مباشر فقط على تسريع الجسم؟ حسنًا ، "ممارسة الضغط" هي مجرد تعبير لفظي لعبارة "تطبيق القوة" - أحد المتغيرين الرئيسيين في الديناميات - والآن يمكننا أن ننتقل إلى نيوتن لمعرفة كيف تؤثر القوى على التسارع. يربط قانون نيوتن الثاني القوة "واو" بمشتق الكتلة - الحجم الثاني للديناميات - أضعاف السرعة. يُطلق على ناتج الكتلة والسرعة "زخم الجسم" ، يُشار إليه بـ p:

$$

$$F = p '= {{dp} \ over {dt}} = {{d (mv)} \ over {dt}} = mv' = ma$$

المعادلة 6

الكتلة ثابتة للسرعات التي نعمل بها الآن ، وهذا يأتي من المشتق في المعادلة 6 ، وحصلنا على المعادلة المعروفة F = ma (على الرغم من أنني متأكد من أن نيوتن حدد في البداية القوة من خلال مشتق الزخم).

إذا كنا نتعامل فقط مع النقاط المادية ، فإن المعادلة 6 هي ما نحتاج إليه في الديناميات. بالنسبة لقوة معينة لنقطة ما ، يتم العثور على التسارع بتقسيم القوة على الكتلة. هذا يعطينا التسارع ، مما سيساعد في حل معادلة الحركة من المثال أعلاه. ومع ذلك ، فإننا نتعامل مع المواد الصلبة ذات الكتلة الموزعة على مساحة معينة (الحجم ، عندما يتعلق الأمر بالعالم ثلاثي الأبعاد) ، لذلك لا نزال بحاجة إلى العمل.

أولاً ، فكر في مادة صلبة كمجموعة من كتل النقاط. سنحدد الزخم الكلي ، pT ، للصلب ، كمجموع زخم جميع النقاط التي تشكل الجسم (أستخدم الفهرسة العليا ، لأنني أريد أن أوضح بشكل أوضح القيم الكمية التي تنتمي إلى هذه النقاط):

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

المعادلة 7

يمكننا تبسيط تحليل ديناميات جسم صلب إلى حد كبير من خلال تقديم مفهوم مركز الكتلة (CM). المتجه الموجه إلى مركز الكتلة هو مجموع خطي للمتجهات موجه من جميع نقاط كتلة الجسم الصلب مقسومًا على كتلة الجسم بالكامل ، M:

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ over {M}}$$

المعادلة 8

باستخدام تعريف مركز الكتلة ، يمكننا تبسيط المعادلة 7 عن طريق ضرب طرفي المعادلة 8 في M ، وتمييزها ، ثم استبدال النتيجة في المعادلة 7:

$$

$${{d (Mr ^ {CM})} \ over {dt}} = {\ sum_ {i} {} {} {{d (m ^ ir ^ i) \ over dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

المعادلة 9

الجانب الأيمن من المعادلة 9 هو الزخم الكلي على النحو المحدد في المعادلة 7. الآن دعونا ننظر إلى الجانب الأيسر من المعادلة: هذه هي السرعة في مركز الكتلة مضروبة في كتلة الجسم كله. حرك الجانب الأيمن إلى اليسار واحصل على:

$$

$$p ^ T = {{d (Mr ^ {CM})} \ over {dt}} = Mv ^ {CM}$$

المعادلة 10

يستنتج من المعادلة 10 أن الزخم الخطي يساوي مجموع أوقات الكتلة بالسرعة الموجهة من مركز الكتلة ، لذلك ليست هناك حاجة للتلخيص في المعادلة 7 من أجل إيجاد الزخم إذا كنا نعرف كتلة الجسم واتجاه ناقل السرعة لمركز الكتلة. علاوة على ذلك ، فإن جميع النتائج النهائية للحسابات تجد مكوّنات للجسم كله ، لكن مركز الكتلة موجود ويبسط بشكل كبير تحديد الزخم الكلي من المعادلة 10 ، لذلك لا يمكننا القلق - لإيجاد الزخم الخطي الذي يمكننا اعتبار الجسم كنقطة مادية مع السرعة والكتلة المعطاة.

بالقياس ، القوة الكلية هي مشتق من الزخم الكلي ، لذلك يمكن استخدام مفهوم مركز الكتلة لتبسيط معادلة القوة:

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

المعادلة 11

باختصار ، يستنتج من المعادلة 11 أنه يمكننا النظر في جميع القوى التي تتفاعل مع مادة صلبة ، كما لو أن ناقلات مجموعها كان لها تأثير على نقطة مركز الكتلة ، التي تحتوي على كتلة الجسم كله. نقسم القوة (اقرأ الجاذبية) على M من أجل إيجاد تسارع مركز الكتلة ، ثم دمج التسارع في الوقت المناسب من أجل الحصول على سرعة وتنسيق الجسم. لأن نتجاهل تأثيرات الدوران حتى المقالة التالية ؛ لدينا بالفعل جميع المعادلات التي نحتاجها لوصف ديناميات الجسم الصلب. لاحظ أن المعادلة 11 لا تحتوي على معلومات حول مكان توجيه القوى المطبقة على الجسم. سينبثق هذا عندما نتعامل مع الزخم الخطي ومركز الكتلة ، ونقوم فقط بتطبيق القوى على CM للعثور على تسارع مركز الكتلة. عندما نحسب دوران الجسم تحت تأثير هذه القوى في المقالة التالية ، سنرى كيف يتم استخدام تنسيق تطبيق القوة.

نشيد الفرح

في هذه المرحلة ، يمكننا النظر في مثال آخر للتكامل التحليلي ، باستخدام المعادلة 11 لإيجاد تسارع مركز الكتلة بدلاً من القيمة المختارة بشكل تعسفي = 5. ومع ذلك ، فإننا نواجه مشكلة خطيرة ، لأن التكامل التحليلي عادة لا يكون له قيمة مطبقة ، لأن الأمر معقد للغاية ، لذلك سنركز على ما يسمى التكامل العددي للمعادلات التفاضلية العادية (ODEs). واو ، والآن يبدو أن الرياضيات الحقيقية! بمجرد أن تتعلم هذا ، سيكون الوقت قد حان لرفع الشريط. لحسن الحظ ، فإن التكامل العددي لل ODEs ليست صعبة كما قد يبدو للوهلة الأولى! لفهم ما يعنيه هذا ، ننتقل من الأقوال إلى الأفعال!

لذلك ، المعادلة التفاضلية هي معادلة تحتوي على مشتقات الكميات التابعة بالإضافة إلى الوظيفة نفسها ، والمتغيرات المستقلة والمعلمات. هذا مطول ، ولكن هنا مثال لقوة متغيرة الوقت في عالم أحادي البعد: F = 2t ، F عبارة عن كمية تابعة ، و t مستقلة. يتم تحديد قيمة F فقط بواسطة F. دع معادلة القوة تعتمد فقط على سرعة جسمنا.تزداد قوة مقاومة الهواء مع زيادة سرعة الطائرة. دعنا نعود إلى المثال في العالم أحادي البعد ، ماذا لو كانت F = -v تعني أن قوة الاحتكاك تبطئ من جسمنا بما يتناسب مع السرعة؟ لدينا مشكلة ، لأننا حلل المعادلة على النحو التالي: F = ma = -v ، وبقسمة m ، حصلنا على (تذكر أن التسارع هو مشتق من السرعة):

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

المعادلة 12

هذه المعادلة التفاضلية ، (معادلة السرعة تحتوي على مشتق السرعة في المعادلة 12) تسمى المعادلة التفاضلية العادية ، لأنها تحتوي فقط على مشتقات عادية بكميات تابعة (على عكس المشتقات الجزئية ، التي تشكل معادلات تفاضلية جزئية [PDEs] ، نحن لسنا حولها سنتحدث).

الآن دعنا ننتقل إلى الجزء التالي من عبارة: التكامل. كيف سبق لنا دمج dv / dt لإيجاد v في ظروف هذه المعادلة؟

سوف يبدو هذا غير معقول ، لكن كل معادلة في الفيزياء تقريبًا تفاضلية ، لذا فقد تمت دراسة المواد المستنفدة للأوزون بشكل جيد. غالبًا ما يمكن العثور على معادلات تفاضلية في الفيزياء ، لأن معدل التغير في الكمية الكمية غالبًا ما يعتمد على الكمية نفسها. على سبيل المثال ، لاحظنا بالفعل أن الكبح (حجم التغير في السرعة) ، بما في ذلك سرعة مقاومة الهواء ، يعتمد على السرعة. أمثلة أخرى من الفيزياء: التبريد (يعتمد معدل فقدان الحرارة على درجة الحرارة الحالية) والانحلال الإشعاعي (يعتمد معدل الانحطاط على مقدار المواد المشعة الموجودة).

إن الكلمة الأخيرة في العبارة - العددية - هي خلاصنا. أقول هذا لأن نظرية التكامل التحليلي للمعادلات التفاضلية ، حتى أبسطها ، ضخمة ومربكة إلى حد ما. على الرغم من المفارقات ، من السهل نسبياً فهم دمج المواد المستنفدة للأوزون باستخدام الأساليب العددية للكمبيوتر. بعد ذلك ، سوف أصف مُدمجًا عدديًا بسيطًا استنادًا إلى طريقة Euler ، وسوف أقوم بتحسينه في المقالة التالية.

تعتمد جميع الدمجات العددية تقريبًا ، ولكن لا يوجد أي صريحة أخرى مثل طريقة Euler ، ببساطة على التعريف القديم للحوسبة من خلال المشتق الأول للميل المائل: تحدد dy / dx ميل y اعتمادًا على x. على سبيل المثال ، إذا كانت لدينا المعادلة الخطية y = 5x ، فإن dy / dx = 5 تعني أن الميل ثابت يساوي 5 لأي x ، وكما يمكنك الافتراض ، فهذا خط مستقيم. مثال أكثر صعوبة قليلاً هو القطع المكافئ y = x2. في هذه الحالة ، dy / dx = 2x ، وهذه دالة لتحديد الميل الجديد لكل إحداثي x. صورت y = x2 في الشكل 2: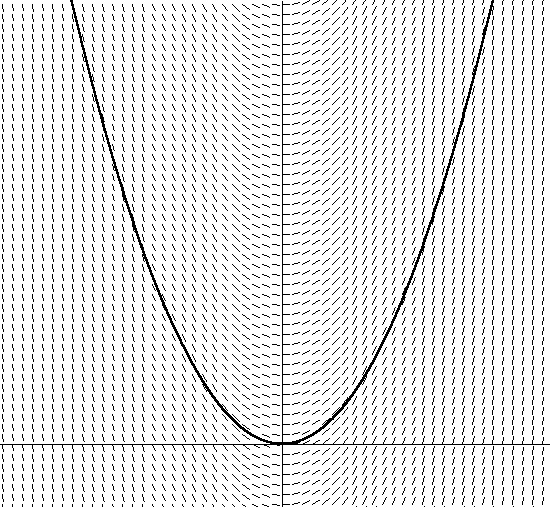



الشكل 2. y = x2

بالإضافة إلى ذلك ، قمت أيضًا بتحريك اتجاه المتجه المائل عن طريق حل المعادلة dy / dx = 2x + C لكل x. انتبه إلى حقيقة أن زاوية المتجه المائل تساوي الظل المائل في زاوية المماس في هذه المرحلة. لاحظ أيضًا أن هناك العديد من القطع المكافئة المختلفة التي ترضي زاوية مجموعة الظلال ، والتي تختلف فقط في التحول على طول المحور ص. يتم الحصول على كل من هذه القطع المكافئة باستخدام ثوابت تكامل مختلفة ، والتي يتم تضمينها في المعادلة dy / dx = 2x + C. تحتوي القطع المكافئة التي قمت بتصويرها على ثابت تكامل يساوي 0. إذا اخترت ثابتًا آخر ، على سبيل المثال ، 1 ، أحصل على المعادلة y = 2x + 1. هذا يعني أن هناك مكافئًا مشابهًا مع تحول 1 وحدة لأعلى للمحور y.

الآن فكر في حقيقة أنه إذا كنت لا تعرف مجال النواقل في الشكل 2 المحدد بواسطة القطع المكافئ ، فقم فقط بالجلوس في بركة. لذلك ، إذا كنت ترغب في حل معادلة الظل ، فأنت بحاجة فقط إلى اتباع اتجاه الموجه في كل نقطة ، وتغيير الاتجاه وفقًا للتغيير في اتجاه مجال المتجه. سوف تفاجأ أنه بعد مرور بعض الوقت ، سترى أنك تسير على طول مسار مكافئ (أو على طول مقطع من القطع المكافئ) ، حسب المكان الذي بدأت فيه. دون إدراك ذلك ، قمت بدمج معادلة حقل المتجه. لقد وجدت مكافئًا معينًا (بناءً على المكان الذي بدأت فيه ، أو على الشروط الأولية) ، باستخدام المعادلة المشتقة فقط (حساب dy / dx أثناء الانتقال في حقل المتجه).

القيام بنفس الشيء لمعادلة تفاضلية حقيقية أمر بسيط أيضًا. بالنسبة لمعادلة تفاضلية من النوع dy / dx = f (x، y) ، فإن إيجاد المشتق dy / dx على شكل الظل إلى f (x، y) يصف زاوية ميل الظل لكل إحداثي على الإحداثي x، y. إذا كنت تخطط لحقل متجه تعطى بواسطة dy / dx = f (x، y) ، فيمكنك اتباع ذلك عن طريق القياس مع القطع المكافئ من خلال إيجاد المشتق في كل نقطة والمتابعة في هذا الاتجاه. يوضح الشكل 2 حقل متجه للمعادلة 12 ، معادلتنا لمقاومة الهواء ، مع السرعة على طول المحور العمودي والوقت على طول الأفقي (اخترت تعسفي m = 1 لهذا الرسم البياني).



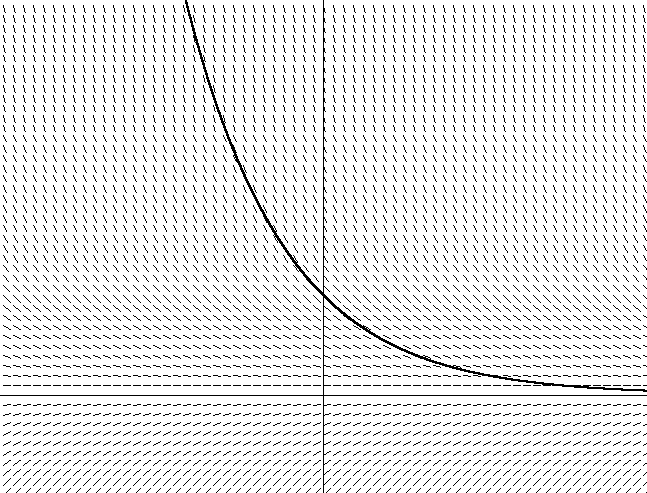الشكل 3. DV / DT = -v / م

يظهر أيضًا أحد المنحنيات العديدة الممكنة. قد تلاحظ أنه إذا اخترت موضع البداية في الرسم البياني (الذي يعتمد على السرعة الأولية في المعادلة) ، فمع مرور الوقت ، سوف تميل السرعة إلى الصفر ، لأن قوة الاحتكاك تبطئ الجسم. يمكنك أيضًا معرفة كيف يعتمد الانخفاض في السرعة على القيمة الحالية للسرعة - كلما تحركت بشكل أسرع ، انخفضت السرعة. يصبح هذا واضحا عندما يتبع نفس الشيء من المعادلة 12.

التكامل العددي يشبه ما فعلناه على الرسم البياني. تتبع خوارزمية أويلر للتكامل العددي ببساطة مجال المتجه وفقًا للموضع الأولي من خلال إيجاد مشتق من المعادلة (-v / m لمثالنا مع قوة الاحتكاك) لتحديد الميل عند النقطة الحالية ، ثم يتحرك للأمام خطوة بخطوة في الوقت المناسب ، وهذا يتوقف ببساطة على قيمة ثابتة من h ، على طول المنحدر. ثم يتم حساب موضع جديد لتحديد الميل الجديد بعد فترة زمنية معينة:

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

أو بتعبير أدق لمعادلة مقاومة الهواء:

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

من الواضح أن طريقة Euler تعطي خطأ بسيطًا في كل خطوة زمنية ، لأن متجه السرعة الحقيقي (وبالتالي منحنى الحل) ينحني مع انحراف في كل نقطة ، وتنحرف خوارزمية Euler قليلاً عن زاوية الميل. ولكن إذا كانت الخطوة الزمنية ، هي كميات صغيرة إلى حد ما ، فإن الخطأ يميل إلى الصفر. سنناقش هذا بمزيد من التفصيل في المستقبل.

هذا هو كل ما تحتاج لمعرفته حول التكامل العددي باستخدام طريقة Euler. قد تسأل كيف سنقوم بدمج السرعة للحصول على الإحداثيات. نحن ببساطة نستخدم طريقة Euler مرة أخرى لدمج dr / dt = v ، تمامًا كما قمنا بدمج dv / dt = a ، عن طريق القياس. نحصل على معادلتين تفاضليتين متصلتين (واحدة أخرى من انتصارنا):

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

هذا يعطينا خوارزمية بديلة لحساب الإحداثيات بعد إجراء أي قوة مطبقة تعسفا على جسمنا (والتي قد تعتمد على السرعة ، كما رأينا ، أو الوقت ، أو حتى موقف أجسادنا وغيرها من الهيئات ، أو في وقت واحد!). بالنسبة إلى طريقة Euler ، لا يهم شكل القوة المطبقة ، لأنه يمكنك حسابها في أي وقت من الأوقات. يهتم أويلر بحجم تأثير القوة على الكتلة ، كما هو مائل ، وهذا كل شيء.
لقد نفدت المساحة ، لذلك ليس لدي أي وسيلة لتوفير روابط. في المرة القادمة سوف أنصح العديد من الكتب الرائعة ، وسنكتشف كيفية حساب دوران المواد الصلبة.

على الرغم من أن جسده ليس صلبًا كما نود ، إلا أن كريس هيكر لديه شخصية ديناميكية. إذا قمت بتطبيق القوة ، فسيجيب على checker@bix.com.

ملاحظات المترجم: يتم تقديم التورية هنا ، يتم تشغيل موضوع المقالة ومحتواها. ملحوظة: يعرب

مؤلف الترجمة عن شكره الخاص لمستخدمي بيريز و MarazmDed على تحريرهم للترجمة. شكرا لك