🕝 👩🏾‍🎓 👗 تحليل المويجات. الأساسيات 🍰 🙂 🐯

مقدمة

الكلمة الإنجليزية المويجات (من الفرنسية "ondelette") تترجم حرفيًا باسم "موجة قصيرة (صغيرة)." في العديد من الترجمات للمقالات الأجنبية إلى الروسية ، هناك أيضًا مصطلحات: "burst" ، "burst function" ، "low-wave function" ، "wave" ، إلخ.

تحويل المويجات (VP) يستخدم على نطاق واسع لتحليل الإشارات. بالإضافة إلى ذلك ، يجد تطبيق كبير في مجال ضغط البيانات. نائب الرئيس لإشارة أحادية البعد هو تمثيلها في شكل سلسلة معممة أو تكامل فورييه عبر نظام من الوظائف الأساسية.

$\ psi _ {ab} (t) = \ frac {1} {\ sqrt {a}} \ psi \ left (\ frac {t-b} {a} \ right)$ ، (1)

شيدت من الأم (المصدر) المويجات

$\ psi (t)$ امتلاك خصائص معينة بسبب عمليات التحول الزمني (ب) وتغيير النطاق الزمني (أ).

عامل

$1 / \ sqrt {a}$ يضمن استقلال قاعدة الوظائف (1) من رقم القياس (أ). بالنسبة للقيم المعطاة للمعلمات a و b ، فإن الوظيفة

$\ psi_ {ab} (t)$ وهناك المويجات الناتجة عن المويجات الأم

$\ psi (t)$ .

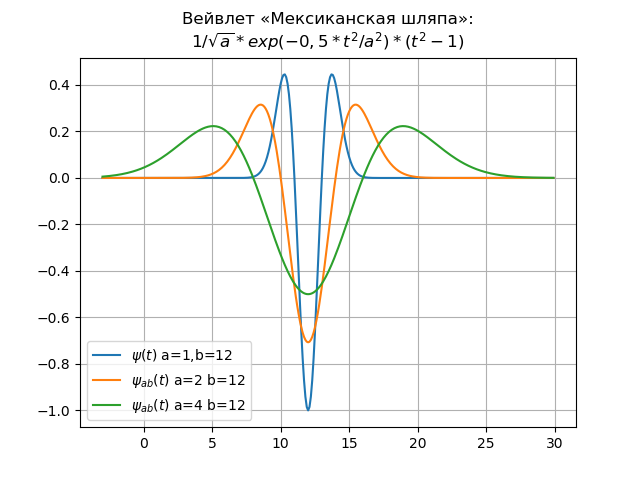
مثال على ذلك المويجات قبعة المكسيكي في مجالات الوقت والتردد:

قائمة المويجات للنطاق الزمني

from numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()

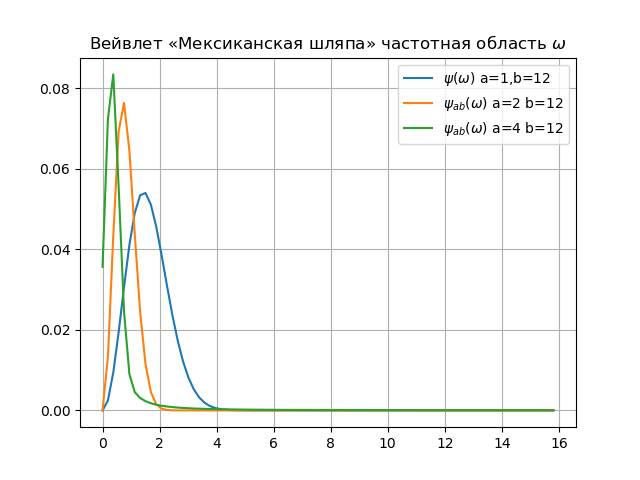
قائمة للطيف المويجات

 from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « »   $\omega$") legend(loc='best') grid(True) show()

الاستنتاج:

1. بين مفهوم التوافقيات فورييه وحجم المويجات ، هناك حقا علاقة. الشيء الرئيسي في هذه العلاقة هو النسبة العكسية من التردد الطبيعي والمقياس. بالإضافة إلى ذلك ، تقليل المقياس ، نزيد عرض النطاق الترددي لطيف المويجات.

2. عن طريق تغيير المقياس (زيادة يؤدي إلى تضييق طيف فورييه للوظيفة

$\ psi_ {ab} (t)$ ) ، تستطيع الموجات الكشف عن الاختلاف في الخصائص على المقاييس المختلفة (الترددات) ، وبسبب التحول ، قم بتحليل خصائص الإشارة في نقاط مختلفة على الفاصل الزمني المدروس بأكمله. لذلك ، عند تحليل الإشارات غير الثابتة ، نظرًا لموقع محلية الموجات ، فإنها تحصل على ميزة كبيرة على تحويل فورييه ، والذي يعطي معلومات عالمية فقط حول ترددات (موازين) للإشارة التي تم تحليلها ، نظرًا لأن نظام الوظائف المستخدمة (الأس أو الجيب المعقدة وجيب التمام) محدد على فاصل لانهائي.

3. تسمح لك القوائم المذكورة أعلاه المكتوبة بلغة Python عالية المستوى الموزعة مجانًا بتحديد وظائف الموجات التي تلبي المتطلبات المحددة. ومع ذلك ، فمن الضروري بالإضافة إلى ذلك أن تأخذ في الاعتبار جميع العلامات الرئيسية للموجات.

العلامات الرئيسية للمويجات

القيود. يجب أن يكون مربع قاعدة الوظيفة محددًا:

ا ل ي س ا ر

$\ اليسار \ | \ psi \ right \ | ^ {2} = \ int _ {- \ infty} ^ {\ infty} \ left | \ psi (t) \ right | ^ {2} dt <\ infty$ . (2)

التعريب. يستخدم VP ، على عكس تحويل Fourier ، وظيفة أولية مترجمة في الوقت المناسب وفي التردد. للقيام بذلك ، يكفي أن الظروف

ا ل ي س ا ر

$\ اليسار | \ psi (t) \ right | \ leq C (1+ \ left | t \ right |) ^ {- 1- \ varepsilon}$ و

ا ل ي س ا ر

$\ اليسار | S _ {\ psi} (\ omega) \ right | \ leq C (1+ \ left | \ omega \ right |) ^ {- 1- \ varepsilon}$ في

$\ varepsilon> 0$ ، (3)

على سبيل المثال ، وظيفة دلتا

د ل ت ا ر

$\ دلتا (ر)$ والوظيفة التوافقية لا تفي بالشرط الضروري للتوطين المتزامن في مجالات الوقت والتردد.

متوسط الصفر. يجب أن يتذبذب الرسم البياني للوظيفة الأصلية (يكون بالتناوب) في نقطة الصفر تقريبًا على المحور الزمني وأن يكون له مساحة صفرية:

$\ int _ {- \ infty} ^ {\ infty} \ psi (t) dt = 0$ . (4)

من هذا الشرط ، يصبح من الواضح اختيار اسم "المويجات" - موجة صغيرة.

يساوي صفر وظيفة المنطقة

$\ psi (t)$ ، أي لحظة الصفر ، يؤدي إلى حقيقة أن تحويل فورييه

$S _ {\ psi} (\ omega)$ هذه الوظيفة تساوي الصفر ل

أ و م ي غ ا

$\ أوميغا = 0$ وله شكل مرشح الفرقة تمرير. بالنسبة للقيم المختلفة (أ) ، ستكون هذه مجموعة من مرشحات ممر الموجة.

غالبًا ما يكون من الضروري للتطبيقات ألا تساوي صفراً فقط ، بل تساوي جميع اللحظات الأولى n صفراً:

$\ int _ {- \ infty} ^ {\ infty} t ^ {^ {n}} \ psi (t) dt = 0$ . (5)

تسمح موجات n-th للشخص بتحليل البنية الدقيقة (ذات التردد العالي) للإشارة ، وقمع مكوناتها المتغيرة ببطء.

التحجيم. سمة مميزة لـ VP هي تشابهها الذاتي. جميع الموجات من عائلة معينة

$\ psi_ {ab} (t)$ لديهم نفس عدد التذبذبات مثل المويجات الأم

$\ psi (t)$ ، منذ الحصول عليها منه عن طريق تحويلات النطاق (أ) والتحول (ب).

تحويل المويجات المستمر

تحويل المويجات المستمر (المتكامل) (NVP أو WT - تحويل المويجات المستمر). نحن نبني الأساس

$\ psi_ {ab} (t)$ باستخدام تحويلات النطاق المستمر (أ) والتحويلات (ب) من المويجات الأم

$\ psi (t)$ مع القيم التعسفية للمعلمات أساس a و b في الصيغة (1).

بعد ذلك ، بحكم التعريف ، يتم كتابة NVP (تحليل) وعكس (توليف) NVP (أي ، PNVP و ONVP) للإشارة S (t) على النحو التالي:

، ،

$W_ {s} (a، b) = (S (t)، \ psi _ {ab} (t)) = \ frac {1} {\ sqrt {a}} \ int _ {- \ infty} ^ {\ infty} S (t) \ psi \ left (\ frac {tb} {a} \ right) dt$ ، (6)

S (t) = \ frac {1} {C _ {\ psi}} \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} ^ {\ infty} W_ {s} (a، b ) \ psi _ {ab} (t) \ frac {dadb} {a ^ {2}}

$S (t) = \ frac {1} {C _ {\ psi}} \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} ^ {\ infty} W_ {s} (a، b ) \ psi _ {ab} (t) \ frac {dadb} {a ^ {2}}$ ، (7)

حيث

$C _ {\ psi}$ - تطبيع معامل ،

$C _ {\ psi} = \ int _ {- \ infty} ^ {\ infty} \ left | \ psi (\ omega) \ right | ^ {2} \ left | \ omega \ right | ^ {- 1} d \ omega <\ infty$
حيث: (• ، •) هو الناتج العددي للعوامل المقابلة ،

$\ mathbf {\ psi (\ omega)}$ - فورييه تحويل المويجات

$\ psi (t)$ . للموجات غير طبيعية

$C _ {\ psi} = 1 دولا$ .

يتبع من (6) أن الطيف المويجات

$W_ {s} (b، a)$ (طيف المويجات ، أو طيف المقياس الزمني) ، على عكس طيف فورييه (طيف واحد) ، هي وظيفة من وسيطين: الحجة الأولى (المقياس الزمني) تشبه فترة التذبذب ، أي هو عكس التردد ، والثاني b –– يشبه إزاحة الإشارة على طول المحور الزمني.

تجدر الإشارة إلى أن

$W_ {s} (b، a_ {0})$ يميز وقت الاعتماد (في

$a = a_ {0})$ ، في حين أن التبعيات

$W_ {s} (a، b_ {0})$ من الممكن مطابقة الاعتماد على التردد (من أجل

$b = b_ {0}$ ).

إذا كانت الإشارة المدروسة S (t) هي نبضة واحدة للمدة

$\ tau_ {u}$ تتركز في الحي

$t = t_ {0}$ ، ثم سيكون لطيف المويجات أعظم قيمة في محيط النقطة مع الإحداثيات

$a = \ tau_ {u} ، b = t_ {0}$ .

طرق العرض

$W_ {s} (b، a)$ قد يكون مختلفا. تتراوح من

$W_ {s} (b، a)$ هو سطح في الفضاء ثلاثي الأبعاد. ومع ذلك ، في كثير من الأحيان بدلاً من صورة السطح ، يتم تقديم إسقاطه على المستوى ab بمستويات iso (أو أشكال بألوان مختلفة) ، مما يجعل من الممكن تتبع التغير في شدة اتساعات EP بمقاييس مختلفة (a) وفي الوقت المناسب (b).

بالإضافة إلى ذلك ، فهي تصور خطوطًا للإطار المحلي لهذه السطوح ، وهو ما يسمى الهيكل العظمي (الهيكل العظمي) ، والذي يكشف عن هيكل الإشارة التي تم تحليلها.

تتحول المويجات المستمرة عند تحديد طيف المويجات بناءً على المويجات الأم - "القبعة المكسيكية".

تستخدم الأمواج الأخرى للأمهات المستخدمة في NVP أيضًا:

يستخدم VP المستمر على نطاق واسع في معالجة الإشارات. على وجه الخصوص ، يوفر تحليل المويجات (VA) فرصًا فريدة للاعتراف بالميزات المحلية "الدقيقة" للإشارات (الوظائف) ، وهو أمر مهم في العديد من مجالات الهندسة الراديوية ، والاتصالات ، والالكترونيات الراديوية ، والجيوفيزياء وغيرها من فروع العلوم والتكنولوجيا. دعونا ننظر في هذا الاحتمال مع بعض الأمثلة البسيطة.

التذبذب التوافقي.

إشارة لديه الشكل:

$s (t) = Asin (\ omega t- \ phi)$

حيث:

$A = 1 V ، \ omega = \ frac {2 \ pi} {T} = \ frac {2 \ pi} {50} ، \ psi = 0$

وظيفة تشكيل المويجات:

$MHAT (t): = \ frac {d ^ {2}} {dt ^ {2}} exp (-t ^ {2} / 2)$ .

المويجات:

$\ psi (a، b، t) = \ frac {1} {\ sqrt {a}} MHAT \ left (\ frac {t-b} {a} \ right)$ .

طيف المويجات: N: = 256 ، a: = 1..30 ، b: = 0..50 ،

$W (a، b): = \ int _ {- N} ^ {N} \ psi (a، b، t) s (t) dt، N_ {ab}: = W (a، b).$ .

قائمة البرنامج

 from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title('  ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- :  ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D-  z = w (a,b)") plt.title(' ab    ', size=12) plt.contourf(X, Y, Z,100) plt.show()

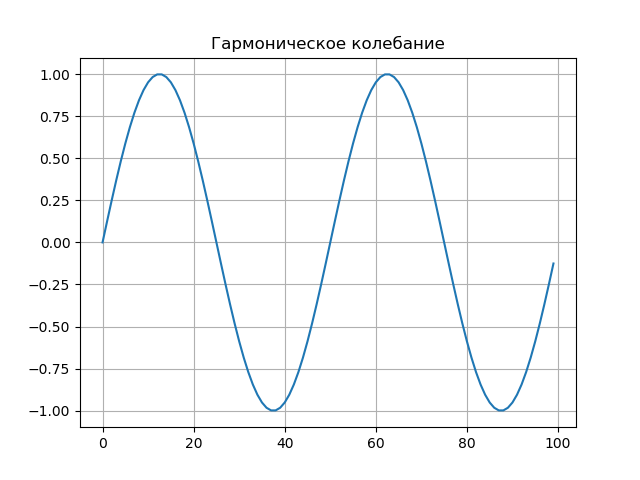
الرسم البياني للإشارة.

رسم بياني لطيف ثنائي المعلمة

$N_ {ab} = W (ab)$ عرض كسطح في الفضاء ثلاثي الأبعاد.

تجدر الإشارة إلى أن القسم W (أ ، ب) للجدول الزمني

$a = a_ {0}$ يميز التذبذب الأولي s (t). علاوة على ذلك ، السعة القصوى في

$a_ {0}: 1 / \ omega$ . اعتمادا على

$W (a_ {0} ، b_ {0})$ يمكن أن تطابق الطيف الحالي من التذبذبات في

$b = b_ {0}$ .

مجموع اثنين من التذبذبات التوافقية.

إشارة لديه الشكل:

$s (t): = A_ {1} sin (\ omega _ {1} t) + A_ {2} sin (\ omega _ {2} t)$

حيث:

$A_ {1} = A_ {2} = 1V ، \ omega_ {1} = \ frac {2 \ pi} {T_ {1}} ، \ omega_ {2} = \ frac {2 \ pi} {T_ {2 }} ، T_ {1} = 50s ، T_ {2} = 10s$ .

$MHAT (t): = \ frac {d ^ {2}} {dt ^ {2}} \ left [e ^ {- t ^ {2/2}} \ right]$ ، N: = 256 ،

$\ psi (a، b، t): = MHAT \ left (\ frac {tb} {a} \ right) ، W (a ، b): = \ int _ {- N} ^ {N} \ psi (a ، b ، t) f (t) dt$ ، a: = 1 ... 30 ، b: = 0 ... 50 ،

$N_ {ab}: = W (a، b)$ .

قائمة البرنامج

 from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure('    ') plt.title('    ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2-  ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D-  z = w (a,b)") plt.title(' ab    ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

الرسم البياني للإشارة.

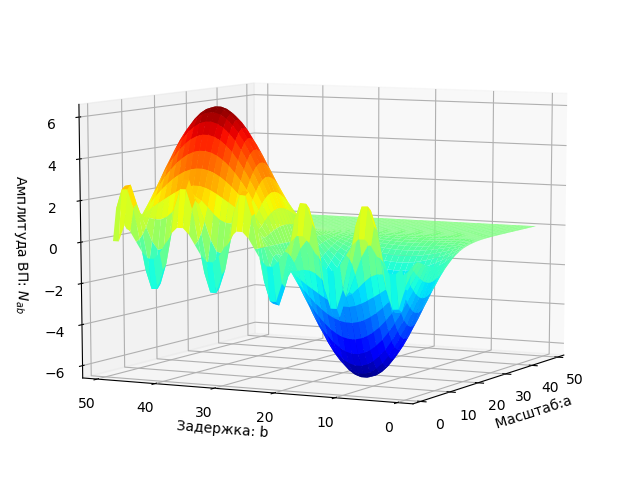
يتم عرض مؤامرة الطيف ثنائي المعلمة W (a، b) كسطح في الفضاء ثلاثي الأبعاد.

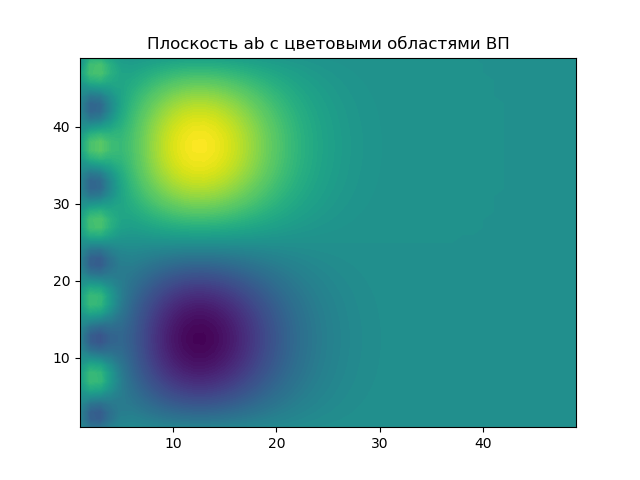
مجموعة المعلمات a، b التي يتم إبراز نتائج EP بها في المناطق الملونة.

يوضح الرسم البياني "المقاطع العرضية" لطيف المويجات لقيمتين للمعلمة a. مع معلمة صغيرة نسبيا من الجدول الزمني أ ، ل

$a_ {1} = 2 (a_ {1}: 1 / \ omega_ {2})$ ، المقطع العرضي للطيف يحمل معلومات فقط حول المكون عالي التردد للإشارة ، مع تصفية (قمع) مكون التردد المنخفض الخاص به.

كما يزيد ، تمديد وظيفة الأساس

$\ psi (\ frac {t-b} {a})$ ، وبالتالي ، تضييق الطيف ، وتضييق عرض النطاق الترددي لل "نافذة" التردد. نتيجة لذلك ، متى

$a_ {2} = 15 (a_ {2}: 1 / \ omega_ {1})$ المقطع العرضي للطيف ليس سوى مكون التردد المنخفض للإشارة.

مع زيادة أخرى في a ، لا يزال نطاق النافذة يتناقص وينخفض مستوى مكون التردد المنخفض هذا إلى مكون ثابت (لمدة> 25) ، وهو ما يساوي الصفر للإشارة التي تم تحليلها.

يوضح الرسم البياني أقسام طيف المويجات W (أ ، ب) التي تميز
الطيف إشارة الحالية في

$b_ {1} = 13$ و

$b_ {2} = 17$ . يحتوي طيف الإشارة المدروسة ، على النقيض من التوافقي ، على مكون عالي التردد في منطقة القيم الصغيرة للجدول الزمني a (a: 1..3) ، والذي يتوافق مع المكون الثاني للإشارة

$A_ {2} sin (\ omega_ {2} t)$ .

زخم مستطيل.

$U: = 5 ، t_ {0}: = 20 ، \ tau: = 60$

$s (t): = \ start {vmatrix} U ، إذا كان t_ {0} \ leq t \ leq t_ {0} + \ tau \\ 0 ، وإلا \ end {vmatrix}$

$MHAT (t): = \ frac {d ^ {2}} {dt ^ {2}} exp \ left (\ frac {-t ^ {2}} {2} \ right)$

$N: = 128 ، \ psi (a ، b ، t): = MHAT \ left (\ frac {tb} {a} \ right) ، W (a ، b): = \ int _ {- N} ^ {N } \ psi (a، b، t) f (t) dt$

$a: = 1..50 ، b: = 0..100 ، N_ {ba}: = W (a، b)$

قائمة البرنامج

 from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D-  ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D-  z = w (a,b)") plt.title(' ab    ', size=12) plt.contourf(X, Y, Z,100) plt.show()

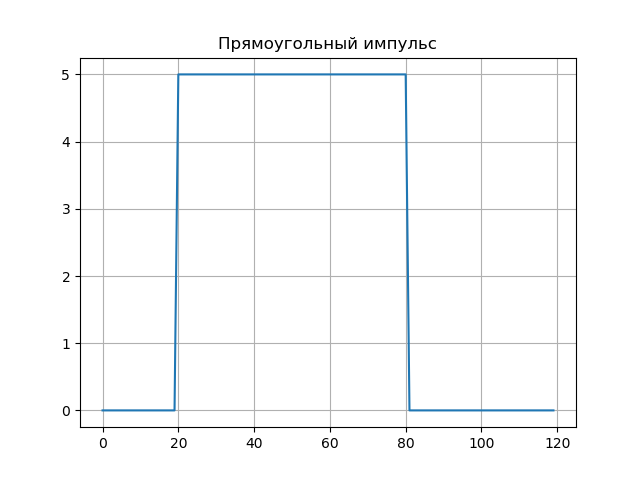
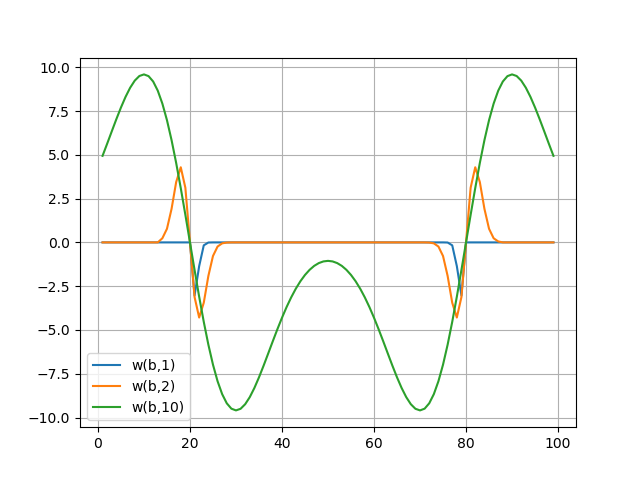
يتم عرض أطياف المويجات في الرسوم البيانية ، كما أن طيف المويجات ينقل بشكل جيد الميزات الدقيقة للإشارة - تقفز على العينات b = 20 و b = 80 (للحصول على: 1..10).

النتائج

هذا المنشور تعليمي بطبيعته ، وهو يوفر معلومات أساسية حول تحليل المويجات بشكل عام ، وأمثلة بسيطة في لغة البرمجة عالية المستوى الموزعة مجانًا تُظهر Python ميزات تحليل المويجات المستمر مع تصويري بياني واسع النطاق وثنائي الأبعاد.

ملاحظة: المؤلف لا ينتقص من المزايا غير المشروطة لتحليل المويجات باستخدام Matlab سواء من حيث عدد المويجات والسرعة. ولكن في بيثون ، لا يزال هناك مجال لمزيد من التطوير: scipy.signal و PyWavelets.

تحليل المويجات. الأساسيات

مقدمة

العلامات الرئيسية للمويجات

تحويل المويجات المستمر

تتحول المويجات المستمرة عند تحديد طيف المويجات بناءً على المويجات الأم - "القبعة المكسيكية".

النتائج

More articles: