مساء الخير ، عزيزي القارئ! هذا هو المقال الثاني المترجم في سلسلة من المقالات حول إنشاء محرك الفيزياء من تأليف كريس هيكر. إذا لم تكن قد تعرفت على الأول حتى الآن ، فإنني أوصي بذلك ، لأن كل شيء سوف يصبح واضحًا على الفور. شكرًا جزيلاً على دعم الترجمة الأولى: من المشجع للغاية أن تعمل أكثر وأكثر! هل لديك قراءة لطيفة!

الفيزياء ، الجزء 2 ، الآثار الزاوية

أردت فقط أن أساند الباب بشيء ثقيل حتى لا يأتي متسلل. هل أطلب الكثير؟ أريد أن تنقلب سيارته وتنفجر في مكان محدد. أريد أن تروس التروس الضخمة قبل أن تتسطح لي. وأريد أن أقوم ببناء شيء يبدو وكأنه أرجوحة ، من أجل اقتياد هبة متوهجة لطيفة من خلال جدار قلعة القلعة. من يستطيع أن يمنعني من ترجمة كل هذا إلى حقيقة؟ أنت تفترض أن خصمي موجود في عالم اللعبة ، ولكن في الواقع - مبرمج للمحرك المادي ، لأن كل ما سبق يستند إلى التأثير الزاوي. يمكنك الاعتماد على الأصابع في تلك الألعاب التي يتم فيها تطبيق تأثيرات الركن ، ناهيك عن العثور على واحدة على الأقل يتم تنفيذها بشكل صحيح.

السبب الرئيسي لعدم تنفيذ التأثيرات الزاوية (أو الدورانية) في الألعاب اليوم هو أن المبرمجين يعتقدون أن الفيزياء التي تصف الحركة الدورانية معقدة للغاية بحيث يتعذر فهمها وترجمتها إلى واقع ملموس. في صفوف الفيزياء في المدرسة الثانوية (حيث تعلمنا جميعًا قانون نيوتن الثاني) لا يتحدثون عادة عن التأثيرات الدورانية ، وليس من الواضح تمامًا كيفية الانتقال من القوة المطبقة على الكائن إلى تدوير هذا الكائن. بطبيعة الحال ، فإن ديناميكيات الحركة الدورانية أكثر صعوبة قليلاً في فهمها من ديناميكيات الحركة الخطية ، ولكنها أبسط مما يبدو. يمكن لأي شخص يمكنه إنشاء محرك مادي وفقًا للمادة المقدمة في المادة الأولى من الدورة أيضًا تضمين التأثيرات الزاوية الموضحة في هذه المقالة. من المأمول أنه بعد نشر هذا المقال ، سيتم تزويد العالم بألعاب تستخدم كل إمكانيات ومزايا تأثيرات الزاوية ، أو على الأقل يمكنك إنشاء لعبة ، عندما تنحني ، يمكنك إطلاق النار على صديقك في ساقه في معركة قاتلة.

التكرار وجيزة

على الرغم من حقيقة أن كل مقالتي حول بعض الموضوعات الفريدة ، فإنني دائمًا ما أعيد قراءة ما كتبته سابقًا ، حتى أفهم أين انتهيت. لقد شاهدت مقالتي الأولى عن الفيزياء ، وأنا مسرور: لقد نجحنا في التعلم كثيرًا ، علاوة على ذلك ، لم نكتب أبدًا رمزًا للبرنامج أو نقرأ الأدبيات الإضافية! قبل أن نبدأ ، دعونا نقوم بتحديث المواد من المقال الأخير.



يحتوي الجدول 1 على أهم الاستنتاجات لديناميات المواد الصلبة. يتبع من المعادلة 1 أن متجه الإحداثيات (r) ، متجه السرعة (v) ، متجه التسارع (a) يرتبطان بالمشتقات (وبالتكاملات ، إذا قرأنا بالترتيب العكسي). للتذكير ، نحتفل بالتمييز الزمني بعلامة (r '). r 'هو نفس dr / dt ، و r' 'هو نفس مشتق المرة الثانية. من المعادلة 2 ، يترتب على ذلك أن القوة مرتبطة بزخم خطي (ناتج الكتلة والسرعة) والكتلة والتسارع. يمكن الحصول على تعريف مركز الكتلة من المعادلة 3 (هذه هي النقطة التي تتوازن فيها جميع الكتل والمسافات مع بعضها البعض). تنص المعادلة 4 على أن الزخم الخطي الكلي للمادة الصلبة هو مجموع كل زخمها ، والذي ، لحظنا ، يساوي ببساطة زخم مركز الكتلة (CM). المعادلة 5 جوهرة حقيقية. يستخدم المعادلة 4 لإثبات أن تسارع مركز كتلة كائن ما يرتبط بالقوة الكلية (متجه مجموع كل القوى المؤثرة على الكائن في وقت معين) من خلال كمية عددية ، كتلة الجسم.

لتلخيص كل ما تم وصفه في المقالة الأولى: علمنا أن القوة الكلية المؤثرة على مركز كتلتنا تساوي مجموع جميع القوى المطبقة على الجسم (بما في ذلك قوة الجاذبية ، عربة الشرير ، انفجار قريب ، قوة محركنا ، إلخ) ) .. بعد ذلك ، قمنا بتقسيم هذا المتجه الإجمالي على كتلة الجسم من أجل الحصول على تسارع CM ، ثم دمج تسارع الوقت للحصول على سرعة وتنسيق الجسم.

المعادلة 5 هي مجرد تحفة! سترى أنه لا يوجد فيه مفهوم لنقاط تطبيق القوى على الجسم ، وهذه نقطة أساسية في تحديد كيفية تدوير الجسم في إطار عملهم. المعادلة 5 صحيحة. في الواقع ، إنها ممتازة لإيجاد التسارع الخطي. نحن في عداد المفقودين نصف المعركة. لكن أول الأشياء أولاً ...

ما هي زاوية الخاص بك؟

في المقالة الأولى ، تم تجاهل الدوران ، لذلك كنا نحتاج فقط إلى ناقل نصف قطر ومشتق منه لوصف تكوين جسمنا في ثنائية الأبعاد. الآن ، دعونا نضيف قيمة حركية أخرى ، الاتجاه (المشار إليها بالحرف الكبير omega - Ω) ، من أجل العمل مع تأثيرات الزاوية. من أجل تعيين Ω ، نحتاج إلى اختيار نظام الإحداثيات بالنسبة للنظام الصلب والإحداثي في ​​عالم اللعبة ، وستكون قيمة equal مساوية للفرق في الزوايا بينهما في الراديان ، كما هو مبين في الشكل 1.



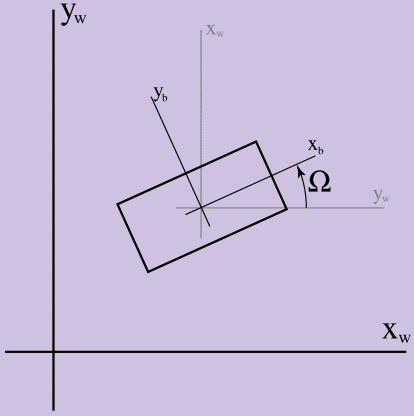الشكل 1. تعريف Ω

في الشكل ، محاور xw ، yw هي محاور الإحداثيات في عالم اللعبة ، و xb ، yb هي محاور إحداثيات المادة الصلبة. greater أكبر من 0 إذا تم حساب عكس اتجاه عقارب الساعة. من المهم هنا توضيح سبب دراستنا لديناميات العالم ثنائي الأبعاد قبل الانتقال إلى الأبعاد الثلاثة: الاتجاه في الأبعاد الثنائية هو كمية عددية (الزاوية بين أنظمة الإحداثيات بالراديان) ، بينما تحديد الاتجاه في العالم ثلاثي الأبعاد أكثر صعوبة.

أثناء دوران الجسم ، تتغير قيمة Ω. يقودنا هذا التغيير إلى حركيات أخرى - السرعة الزاوية (يشار إليها بالحرف الصغير omega - ω). على عكس السرعة الإحداثية والخطية للجسم ، لا نشير إلى السرعة الزاوية كما يلي - Ω. ومع ذلك ، فإننا نشير في بعض الأحيان إلى مشتق السرعة فيما يتعلق بالوقت ، أو التسارع الزاوي ، مثل ω '(هذه قيمة حركية أخرى) أو α (ألفا صغيرة). لا تلومني: لم أتوصل إلى كل هذه التسميات ؛ وفي كل كتاب أقرأه ، هناك اختلافات طفيفة. النظير الزاوي للمعادلة 1 هو:

$$عرض $$ $ {d ^ 2 Ω \ over {dt ^ 2}} = {dω \ over {dt}} = ω '= α $$ عرض $$

المعادلة 6

كما في المعادلة 1 ، نفرق في الوقت المناسب للحصول على α ؛ وإذا تم دمج α بمرور الوقت ، فسوف نحصل على etc. ، إلخ. كل ذلك من خلال القياس مع المقالة السابقة: معرفة التسارع الزاوي لـ α ، يمكننا دمجها مرتين للحصول على اتجاه جديد. ولكن النقطة الأساسية هنا هي معرفة قيمة α.

كما يمكنك أن تتخيل ، فإن هدفنا من هذه المقالة هو استخلاص تناظرية الزاوية لكل من المعادلات الخطية في الجدول 1 ، وبعد ذلك ، مع مراعاة المعادلات الخطية والزاوية والقوة المطبقة على الكائن ، يمكننا حساب التسارع الخطي a والتسارع الزاوي α. أخيرًا ، يمكننا دمج هذه التسارع عدديًا للعثور على مواقع وتوجهات جديدة لأجسامنا.

بادئ ذي بدء ، سنربط الكميات الخطية والزاوية معًا. وهذه خدعة غير واضحة إلى حد ما تستخدم فيها السرعة الزاوية. عند حساب الديناميات ، نحتاج غالبًا إلى العثور على سرعة نقطة تعسفية على كائن. على سبيل المثال ، عندما نحسب اصطدام المواد الصلبة ، نحتاج إلى معرفة سرعة نقاط التصادم من أجل فهم مقدار تأثيرها على بعضها البعض. إذا كانت أجسامنا لا تدور ، فإن سرعة كل نقطة من الجسم هي نفسها. يمكننا ببساطة رصد سرعة مركز كتلة الجسم ، وسيكون ذلك كافيًا. بينما تدور أجسامنا ، يمكن أن يكون لكل نقطة من هذه الهيئات سرعة مختلفة. من الواضح أننا لا نستطيع حساب سرعة عدد لا حصر له من النقاط في جسمنا الصلب ، وبالتالي نحن بحاجة إلى حل مختلف وأفضل.

إحدى الطرق البسيطة التي يتم استخدامها للعثور على السرعة الخطية لأي نقطة داخل كائن ما تستخدم السرعة الزاوية للكائن. النظر في القضية عندما يدور الجسم فقط حول نقطة واحدة ثابتة ، دون تغيير إحداثيات الجسم. أي أن الجسم يدور لكنه لا يتحرك. من المعادلة 7 ، تتبع كيفية حساب سرعة النقطة B للجسم الدوار:

$$عرض $$ $$ v ^ B = ωr ^ {OB} _⟂ $$ عرض $$

المعادلة 7

نحتاج إلى توضيح بضع نقاط في المعادلة 7 ، دعنا نقضي بعض الوقت في هذا. أولاً ، استخدم الفهرسة العليا لإظهار المعلمة التي تنتمي إلى هذه النقاط ، لذلك v ^ B هي ناقل السرعة للنقطة B في الجسم. وبالمثل ، يشير r ^ OB إلى ناقل متجه من مركز دوران جسمنا O إلى النقطة B. الحرف المقلوب المضحك T هو "العامل العمودي" الذي يعمل على المتجه (مثل المتجه r في المعادلة 7) ويدوره 90 درجة عكس اتجاه عقارب الساعة السهم. بمعنى آخر ، يتم إنشاء ناقل جديد متعامد مع القديم. في عالم ثنائي الأبعاد ، يكون المتجه متعامدًا إلى (س ، ص) فقط (س ص). يمكنك بسهولة التحقق من كلماتي على ورقة ورقة الرسم البياني. دعنا نتحدث أكثر عن هذا. يتم تحديد حجم المتجه العمودي بواسطة السرعة الزاوية ω وتعيين السرعة الخطية v ^ B. في المعادلة الروسية ، تظهر المعادلة 7 أن سرعة نقطة من الجسم الدوار يتم حسابها بضرب المتجه العمودي المرسوم من مركز الدوران بواسطة السرعة الزاوية. كيف أفهم ذلك؟ حسنًا ، قرأت عنها في الكتاب ، لكن من الواضح أن هذا التفسير لا يكفي ، لذلك نثبت أن هذا صحيح.

دعنا نثبت حقيقة استنتاجات المعادلة 7 على مرحلتين. أولاً ، نثبت أن قيمة ناقل السرعة الناتج صحيحة ؛ ثم - أن اتجاهه هو الصحيح. بالنسبة للجزء الأول من الدليل ، فكر في الشكل 2.



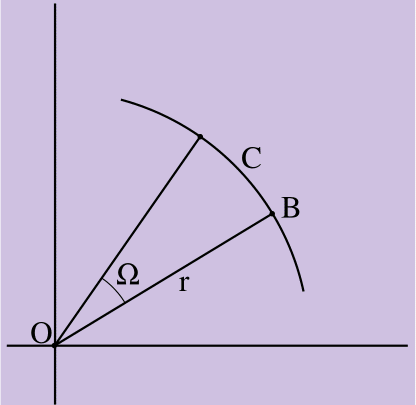الشكل 2. C = Ωr

يوضح الشكل 2 دوران النقطة B بزاوية تساوي Ω راديان على طول دوران جسم صلب مع متجه نصف قطر بطول r موجه من مركز دوران الجسم O إلى النقطة B. B مرت بطول القوس C ، حيث C = fromr من تعريف الراديان. (قياس راديان لزاوية ما هو مقياس قوس مقيد بنصف قطر دائرة. محيط الدائرة هو C = 2πr لأن المقياس الراديان لقوس الدائرة هو 2π [أو 360 درجة]).

سرعة نقطة هي تغيير في إحداثياتها في الوقت المناسب. لذلك ، يمكننا أن نجد سرعة النقطة B - بمعنى آخر ، حجم متجه السرعة - من خلال التمييز بين معادلات الحركة فيما يتعلق بالوقت. C = Ωr هي معادلة الحركة.

$$

$${d (Ωr) \ over {dt}} = {dΩ \ over {dt}} r = ωr$$

يُؤخذ نصف القطر من علامة التمايز ، لأنه ثابت (النقطة B تدور ببساطة ، دون حركة خطية) ، ومشتق الوقت ω هو من المعادلة 6. لذلك ، فإن حجم المتجه B هو متجه السرعة ωr.

من خلال النظر في المعادلة 7 ، نلاحظ أن حجم متجه السرعة صحيح ، لأن العمودي لا يؤثر على طول المتجه و r ^ OB هو ناقل نصف قطره موجه من O إلى B. Fuh ، نحن في منتصف الطريق.

من أجل التحقق من صحة اتجاه متجه السرعة في المعادلة 7 ، فلنبدأ بالتأكد من أن متجه السرعة يجب أن يكون متعامدًا مع متجه نصف القطر. هذا الافتراض مفهوم بشكل حدسي ، لأن النقطة التي تدور حول نقطة معينة أخرى يمكن أن تتحرك فقط بشكل عمودي على المتجه بين هذه النقاط. لا يمكن أن يقترب من مركز الدوران أو الابتعاد عنه ، أو أن هذه الحركة ستتوقف ببساطة عن الدوران. يمكننا أن نؤيد افتراضنا من خلال العمليات الحسابية للمتجهات ، لكنني مقيد في إطار معين لحجم المقالة ، لذلك نحن نفترض أن افتراضنا صحيح. (إذا كنت حريصًا على إثبات ذلك بنفسك ، فقم بالتمييز بين المنتج القياسي للناقل ذي الطول الثابت من تلقاء نفسه.)

أخيرًا ، يجب أن نتأكد من تحديد المتجه بشكل صحيح ، لأن الشكل يوضح متجهين متساويين الطول عموديًا على نصف القطر: v و -v. نظرًا لأن قيمة measured تُقاس بعكس اتجاه عقارب الساعة ، ω> 0 عندما تدور النقطة في اتجاه عقارب الساعة. النقاط العمودية في اتجاه عقارب الساعة ، كما يفعل متجه نصف القطر. يوضح الشكل 3 الاستنتاجات من المعادلة 7:



الشكل 3. العلاقة بين السرعة الخطية والزاوي

تكملة المعادلة 7 لوصف دوران الأجسام المتحركة. نحن نعتبر حركة الجسم الصلب بمثابة حركة بسيطة لمركز دوران الجسم وتناوب بسيط لبقية الجسم حول هذه النقطة. بالنسبة لأولئك المهتمين ، هذه هي نظرية شال في تصنيف الحركات.

تقسم نظرية تشال حركتنا إلى عنصرين - خطي وزاوي. دع مركز دوران الجسم O هو النقطة المتحركة الوحيدة ، ثم نستخدم ω لحساب الدوران حول النقطة O ، وهذا يعطينا الشكل العام للمعادلة 7:

$$عرض $$ $$ v ^ B = v ^ O + ωr ^ {OB} _⟂ $$ عرض $$

المعادلة 9

تقول المعادلة 9 أنه يمكننا حساب سرعة أي نقطة من الجسم المتحرك باستخدام السرعة الخطية لمركز دوران الجسم ، بالإضافة إلى السرعة المكتسبة أثناء دوران الجسم.

سبب الدافع لدينا

الآن يمكننا أن نكتب التماثل الزاوي للمعادلة 2 ، معادلة القوة. نبدأ بتحديد الزخم الزاوي ، L ^ AB لنقطة معينة B ، حول نقطة أخرى A:

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \ الأوقات {\ vec p} ^ B$$

المعادلة 10

تختلف لحظة زخم نقطة ما عن الزخم الخطي لنقطة ما في أن النسخة الزاوية للمعادلة تأخذ في الاعتبار موقع الجسم في الفضاء. من هنا ، يجب قياس الزخم الزاوي لنقطة ما في مكان آخر في عالم اللعبة ، على عكس النبض الخطي ، المصمم لنقطة معينة (ناتج كتلته وسرعته). يظهر هذا من خلال الفهرس العلوي في المعادلة 10. يشير الرمز L ^ AB إلى أن الزخم الزاوي يُقاس للنقطة B من النقطة A (مركز دوران الجسم). تخيل سهمًا يشير من النقطة أ إلى النقطة ب. هذا السهم هو متجه نصف القطر بين نقطتين ، فهذا يعني r ^ AB. لذلك ، فإن الزخم الزاوي لنقطة ما هو نتاج عددي لمتجه زخم خطي ومتجه نصف قطره عمودي عليه. تسمى هذه العملية "المنتج القياسي مع عمودي" ، وهو تناظري ثنائي الأبعاد لمنتج ناقل ثلاثي الأبعاد ، لكننا سنناقشه مرة أخرى.

إذا وصفت بيانياً ما يلي من المعادلة 10 ، على الورق - كما فعلت في الشكل 4 - سترى أنه يحدد مقياس كيفية "الدوران" حول النقطة الخطية للنقطة B.



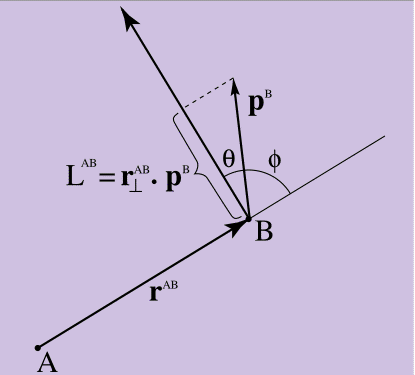الشكل 4. لحظة الدافع

كل شيء صحيح إذا كان الزخم من النقطة B يشير مباشرة إلى النقطة A ، المعادلة 10 = 0 (بما أن العمودي على r يشكل زاوية صحيحة مع p ، وسيكون المنتج القياسي 0). كلما زاد الزخم B الموجه عموديًا إلى A ، زاد الزخم. كما هو مبين في الشكل 4 ، يحتوي المنتج القياسي في المعادلة 10 كمعلم له على جيب تمام الزاوية θ المحصور بين r العمودي r ^ AB إلى p ^ B. إذا نظرت إليه من ناحية أخرى ، فإن حجم المنتج القياسي يعطى بواسطة جيب الزاوية φ بين الأصلي ، وليس عمودي r ^ AB و p ^ B (الجيب هو مفتاح آخر لكشف العلاقة بين المتجه والمنتج العددي). تقدم المعادلة 10 مقياسًا لمقدار الزخم في النقطة "ب" في "الاتجاه الدوراني" بالنسبة إلى النقطة أ.

كما استخدمنا مشتق الزخم الخطي لتحديد القوة ، سنستخدم مشتق الزخم الزاوي لتحديد التوأم الزاوي للقوة - لحظة القوة (يشار إليها بالحرف الصغير tau - τ).

$$

$$τ ^ {AB} = {dL ^ {AB} \ over dt} = {d ({\ vec r} ^ {AB} \ times {\ vec p} ^ B) \ over dt} = \ vec r ^ { AB} \ times ma ^ B = \ vec r ^ {AB} \ times F ^ B$$

المعادلة 11

لتوفير المساحة ، خدعت قليلاً في المعادلة 11 ، وتخطيت بضع خطوات صعبة تنطوي على إيجاد المشتقات. مما تقدم ، يترتب على ذلك أن لحظة القوة مرتبطة بالقوة في مرحلة معينة من خلال منتج العددية.

أخيرًا ، حصلنا على معادلة ديناميكية تستخدم نقطة تطبيق القوة ، والتي تم تجاهلها مسبقًا في معادلات الزخم الخطي. تستخدم المعادلة 11 منتجًا قياسيًا ذو عموديًا كمقياس لمدى القوة المطبقة على النقطة B تدور حول النقطة A ؛ وتسمى هذه "القوة الدورانية" لحظة القوة. تسمح لك المعادلة 11 بالعثور على القيمة العددية للحظة القوة - وبالتالي الزخم الزاوي ، إذا دمجنا لحظة القوة ، ومعرفة القوة المطبقة ونقطة التطبيق.

ومع ذلك ، لم نتلق بعد معادلة العلاقة بين لحظة القوة والمقدار الزاوي للحركيات التي نحتاجها لتدوير الكائن حول محوره - مثل التسارع الزاوي أو السرعة الزاوية أو الاتجاه. لذلك ، لا يمكننا المضي قدمًا قبل استخلاص بعض المعادلات القليلة.

اللحظة التي كنا ننتظرها جميعًا

قبل أن نربط بين الديناميات والحركية ، نحتاج إلى تحديد الزخم الزاوي الكلي ، عن طريق القياس مع الطريقة التي حددنا بها الزخم الخطي الكلي في المعادلة 4. لم أنس المكافئ الزاوي لمركز الكتلة في المعادلة 3 ؛ سوف نرى ذلك في معادلة الزخم الزاوي الكلي.

يرمز L ^ AT إلى الزخم الكلي الزاوي بالقرب من النقطة A ويتم تحديده بواسطة المعادلة 12:

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ times p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ times m ^ iv ^ i}}$$

المعادلة 12

المعادلة 12 هي مجموع كل الزخم الزاوي لجميع نقاط الجسم ، تقاس نسبة إلى النقطة أ. على الجانب الأيمن ، استخدمت تعريف الزخم الخطي من أجل تمثيل p ^ i كمنتج للكتلة والسرعة (mv). سيكون هذا مفيدًا لي في المستقبل من أجل جعل شيء من المعادلة 12 ذو طابع تطبيقي أكثر وضوحًا. تقول المعادلة أنه لإيجاد الزخم الزاوي الكلي لجسمنا ، من الضروري جمع الزخم الزاوي لجميع نقاطه. بالنسبة للجسم الصلب الذي يتكون من الوجوه (وليس من نقاط منفصلة) ، من الضروري حساب التكامل ، مقابل مبلغ غير منفصل.

لحسن الحظ ، يمكننا تبسيط حساباتنا من خلال إدخال كمية جديدة تسمى "لحظة الجمود" ، على غرار الطريقة التي قدمنا ​​بها مركز الكتلة لتبسيط معادلة الزخم الإجمالية. أذكر أنه بفضل المعادلة 7 ، يمكننا أن نجد سرعة نقطة ما من خلال السرعة الزاوية. دع النقطة A في المعادلة 12 هي مركز الدوران من المعادلة 7 ، ومؤشر الجمع i في المعادلة 12 يكون النقطة B من المعادلة 7 ، ثم يمكن تحويل المعادلة 7 إلى المعادلة 12. نحصل على:

$$

$$L^{AT} = \sum _{ i} {\vec r ^{Ai} \times m^i ω \vec r^{Ai}} = ω {\sum _{ i} {m^i \vec r^{Ai} \times \vec r ^{Ai}}} = ω \sum_{ i} {m^i (\vec r ^{Ai})^2} = ωI^A$$

المعادلة 13

سأكتب المعادلة 13 بمزيد من التفصيل ، خطوة بخطوة. أولاً ، نستبدل المعادلة 7 بـ 12 للحصول على المجموع في المعادلة 13. هذا الاستبدال يسمح لنا بوصف الزخم الزاوي باستخدام السرعة الزاوية. بعد ذلك ، نأخذ ω للمبلغ ، لأنه يساوي جميع نقاط المادة الصلبة (يتم تحديد السرعة الزاوية للجسم كله ، وليس لكل نقطة على حدة) ، ونكتب الكتلة مع الفهرس i على اليسار ، من أجل رؤية نصف قطر المنتج القياسي بشكل أوضح -محركات لأنفسهم. هذا المنتج القياسي يساوي مربع طول متجه نصف القطر (المنتج القياسي لأي متجه بمفرده = مربع طوله. تذكر أن العامل المتعامد لا يغير طول المتجه.). أخيرًا ، نكتب I ^ A للدلالة على لحظة الجمود حول النقطة A.

تعتبر لحظة القصور الذاتي للمادة الصلبة ثنائية الأبعاد عددًا جيدًا للغاية ، لأن النقاط التي تشكل الجسم لا يمكنها تغيير كتلتها أو الابتعاد عن مركز الدوران. كنتيجة لهاتين الخواصتين ، يكون المجموع في المعادلة 13 ثابتًا لكل هيئة ، حتى نتمكن من حسابه. متحدثًا بالروسية ، I ^ A هي مجموع المسافات المربعة من النقطة A إلى جميع نقاط الجسم الأخرى ، ويتم قياس كل مسافة وفقًا لكتلة كل نقطة. تمامًا مثل مركز الكتلة - إذا كان الجسم أكثر صلابة من تكوين نقاط منفصلة ، فستتحول المبالغ إلى وحدات متكاملة. وستبقى لحظة الجمود كما هي في الحجم وسيكون لها نفس المعنى المادي.

تحديد لحظة القصور الذاتي بالقرب من نقطة ما أمر مطول ، لكن فكر في I ^ A كمقياس لمدى صعوبة تحويل الجسم إلى النقطة A. على سبيل المثال ، تخيل قلم رصاص (قلم رصاص مسطح). إذا قمنا بقياس لحظة القصور الذاتي بالقرب من مركز القلم ، فسنحصل على قيمة معينة تساوي مجموع مربعات المسافات المقاسة وفقًا لكتلة كل نقطة. بينما إذا قمنا بقياس القصور الذاتي عند طرف نفس القلم الرصاص ، فإننا نحصل على قيمة أكبر ، لأنه كلما تمت إزالة النقاط ذات الكتلة ، زادت قيمة مربعات مسافاتهم. سنقوم هنا بصياغة ما هو بديهي رياضياً: إن تدوير قلم رصاص حول مركزه أسهل بكثير (اقرأه يتطلب جهداً أقل) من تدويره حول أحد الطرفين.

أخيرًا ، نحن على استعداد لربط العلاقة بين المعادلات الزاوية للديناميكيات والمعادلات الزاوية للحركية. إذا قمنا بتمييز المعادلة 13 ، فسنحصل على اللحظة الكلية للقوة على اليسار ، وكان ناتج لحظة الجمود والتسارع الزاوي على اليمين (I ^ A ثابت ، وضعناه خارج علامة التمييز):

$$

$$τ^{AT} = {dL^{AT} \over dt} = {d( I^A ω) \over dt} = I^A ω = I^A α$$

المعادلة 14

هذه المعادلة هي المعادل الزاوي للمعادلة 5؛ في الحقيقة ، إنها F = ma للديناميكيات الزاوية. هذه هي معادلة الصلة بين اللحظة الكلية للقوة والتسارع الزاوي للجسم عن طريق القصور الذاتي في القصور الذاتي. إذا علمنا لحظة القوة التي تمارس على أجسامنا ، يمكننا أن نجد تسارعها الزاوي ، ثم السرعة الزاوية والاتجاه في الفضاء من خلال التكامل - تقسيم لحظة القوة على لحظة الجمود.

خوارزمية ديناميكية

بالكاد يرانا من خلال هذه الدوامة من المعادلات ، ولكن كلها جزء لا يتجزأ منها. لقد استخلصنا معادلات كافية للحصول على ديناميات رائعة لعالم ثنائي الأبعاد مع قوى تعسفية ولحظات من القوى التي تحرك كائناتنا وتدورها. كيفية استخدام هذه المعادلات؟ أدناه هي الخوارزمية الأساسية:

1. ابحث عن قيمة مركز الكتلة ولحظة القصور الذاتي في وسط الكتلة.
2. اضبط الإحداثيات الأولية للجسم واتجاهه في الفضاء وسرعاته الخطية والزاوية.
3. تأخذ في الاعتبار جميع القوى المؤثرة على الجسم ونقاط تطبيقها.
4. أوجد ناتج كل القوى وقسمه على كتلة الجسم من أجل إيجاد التسارع الخطي لمركز الكتلة (المعادلة 5).
5. , , , ( 11).
6. ( 14).
7. , , ( ).
8. , 3.

في الخوارزمية أعلاه ، لا يوجد سوى خطوتين لم أشرحهما. أولاً ، كيفية حساب لحظة القصور الذاتي في الخطوة 1 لكائن صلب؟ ثانياً ، كيف يمكن حل المشكلة مع قوى الخطوة الثالثة؟ يمكن العثور على إجابة السؤال الأول في مثال رمز بسيط ، والذي سأتركه في التطبيق في نهاية هذه المقالة (ستقوم بدمج الكائن حسب منطقته). تحتوي العديد من الكتب على الديناميات على اللحظة المحسوبة من القصور الذاتي لأشكال الكائنات التي يتم مواجهتها بشكل متكرر في التطبيق في النهاية ، لذلك لا يتعين عليك عرضها بنفسك في كل مرة.

تعتمد إجابة سؤال كيفية حساب القوى من الخطوة 3 على التطبيق ، لكنني سأقدم بعض التوصيات العامة. أولاً ، إن قوى مثل الجاذبية ، الموجهة دائمًا في اتجاه واحد (لأسفل ، في حالة الجاذبية) ، لا تخلق لحظة من القوة ، لأنها تسحب كل النقاط في نفس الوقت في نفس الاتجاه ، على الرغم من أننا نحن نطبق هذه القوات مباشرة على مركز الكتلة. يتم تطبيق قوى مماثلة للقوة المرنة على نقطة معينة من الكائن ، فإنها ستخلق لحظة من القوة ، وبالتالي فإننا نعتبرها في الحالة العامة. كما رأينا في المقالة الأولى ، فإن قوة الاحتكاك هي نفس القوة الموجهة في الاتجاه المعاكس لسرعة الجسم.

يمكنك إنشاء نموذج مادي بسيط يوضح قوة الاحتكاك ، وتطبيق القوة فقط على مركز الكتلة ، أو يمكنك اختيار أجزاء الكائن التي ستطبق قوى الاحتكاك ، والقيام بذلك ، والذي يمكن أن يخلق لحظة من القوة تعمل على الكائن. القوى التي تواجهها الهيئات في التصادمات هي أكثر صعوبة بعض الشيء ، وسنتعرف عليها في المقال التالي. يجب اعتبار القوى مثل قوة دفع محرك الصواريخ بمثابة قوى ذات نقطة تطبيق (في هذه الحالة ، إذا فشل أحد المحركات ، فستبدأ في الدوران حول محورها حتى تقوم بضبط عجلة القيادة لموازنة لحظة القوة!). إذا كنت تريد شيئًا مشابهًا لأشعة الجاذبية من جسم غامض ، فيجب أن تُحسب هذه القوة كقوة الجاذبية ولا تخلق لحظة قوة ، أو ينبغي تطبيقها على نقطة محددة على الكائن ،وسوف تدور حول هذه النقطة في حين ترتفع؟ الخيار لك. النقطة الأساسية هي عدم الخوف من تجربة قوى مختلفة محسوبة بطرق مختلفة ، لأنه لديك الآن محاكي حقيقي للرسومات ثنائية الأبعاد ، جرب أنواعًا مختلفة من القوى!

تركت جميع الشفرات والروابط التي تحتاجها على موقع الويب الخاص بي لأنه لم يعد هناك مساحة متبقية. في تطبيقي البسيط ، قمت بتطبيق خوارزمية ديناميات عالم ثنائي الأبعاد ، كما قمت بإضافة كائنات مثبتة في فصل الربيع ؛ تدور حول محورها ، وأحيانًا تصطدم بالجدران ، وتدور. لكنني سأتحدث عن هذا مرة أخرى. اتبع الرابط لمزيد من الأدبيات وتطبيق بسيط لنظامي التشغيل Windows 32 و Macintosh.

نادرًا ما يختبر كريس هيكر تأثير لحظة القصور الذاتي ، ولكنه عادة ما يمر بسرعة كبيرة. يمكن تطبيق القوات على checker@bix.com.

ملاحظات المترجم: يتم تقديم التورية هنا ، يتم تشغيل موضوع المقالة ومحتواها.

ملاحظات PS هو موضع ترحيب. تعليقاتكم يمكن أن تحسن نوعية العمل. شكرا لك

PPS ترجمة المؤلف يعبر عن شكر خاص للمستخدمين berez و باسل Tereshkov لإجراء تغييرات الترجمة. شكرا لك