مصفوفات الهوائي التكيفي: كيف يعمل؟ (أساس)

يوم جيد.

خلال السنوات القليلة الماضية ، كرّست جهودي للبحث وإنشاء خوارزميات مختلفة للمعالجة المكانية للإشارات في صفائف الهوائي التكيفي ، وما زلت أقوم بذلك كجزء من عملي في الوقت الحالي. هنا أود أن أشارك المعرفة والرقائق التي اكتشفتها. آمل أن يكون ذلك مفيدًا للأشخاص الذين يبدأون في دراسة هذا المجال من معالجة الإشارات أو المهتمين فقط.

ما هو مجموعة هوائي التكيف؟

صفيف الهوائي هو مجموعة من عناصر الهوائي ، مرتبة بطريقة ما في الفضاء. لتبسيط هيكل صفيف الهوائي التكيفي ، الذي سننظر فيه ، يمكن تمثيله في النموذج التالي:


غالبًا ما تسمى صفائف الهوائي التكيفي "الهوائيات الذكية" (الهوائيات الذكية ). يتم تصنيع صفيف الهوائي "الذكي" بواسطة وحدة معالجة الإشارات المكانية والخوارزميات المنفذة فيه. تقوم هذه الخوارزميات بتحليل الإشارة المستقبلة وتشكيل مجموعة من الأوزان$$ $ inline $ w_1 ... w_N $ inline $ التي تحدد السعة والمرحلة الأولية للإشارة لكل عنصر من العناصر. يحدد توزيع طور الاتساع المحدد نمط الاتجاهية للشبكة بأكملها ككل. تعد القدرة على تجميع مخطط إشعاع الشكل المطلوب وتغييره أثناء معالجة الإشارة واحدة من الميزات الرئيسية لصفائف الهوائي التكيفي ، والتي تسمح بحل مجموعة واسعة من المشكلات . لكن أول الأشياء أولا.

كيف يتم تشكيل نمط الإشعاع؟

يميز مخطط الإشعاع قدرة الإشارة المشعة في اتجاه معين. للبساطة ، نضع عناصر شعرية متساوي التوتر ، أي لكل منهم ، لا تعتمد قوة الإشارة المنبعثة على الاتجاه. يتم الحصول على تضخيم أو توهين القدرة المشعة بواسطة المصفوفة في اتجاه معين بسبب تداخل الموجات الكهرمغنطيسية المنبعثة من عناصر مختلفة من مجموعة الهوائي. يكون نمط التداخل المستقر لـ EMW ممكنًا فقط إذا كان متماسكًا ، أي يجب ألا يتغير اختلاف الطور الخاص بالإشارات مع مرور الوقت. في الحالة المثالية ، ينبغي لكل عنصر من عناصر مجموعة الهوائي أن ينبعث منه إشارة توافقية على نفس تردد الموجة الحاملة$$ $ inline $ f_ {0} $ inline $ . ومع ذلك ، في الممارسة العملية ، من الضروري العمل مع إشارات ضيقة النطاق لها طيف من العرض المحدود$$ $ inline $ \ Delta f << f_ {0} $ inline $ .
دع جميع عناصر AR تنبعث منها نفس الإشارة بسعة معقدة$$ $ inline $ x_n (t) = u (t) $ inline $ . بعد ذلك ، في المستقبل البعيد ، يمكن تمثيل الإشارة المستلمة من العنصر nth في شكل تحليلي :

$$عرض $$ $$ a_n (t) = u (t- \ tau_n) e ^ {i2 \ pi f_0 (t- \ tau_n)} عرض $$ $$

حيث$$ $ inline $ \ tau_n $ inline $ - تأخير نشر الإشارة من عنصر الهوائي إلى نقطة الاستقبال.
مثل هذه الإشارة هي "شبه متناسق" ، ولتلبية حالة التماسك ، من الضروري أن يكون التأخير الأقصى في انتشار الموجات الكهرومغناطيسية بين أي عنصرين أقل بكثير من الوقت المميز لتغير غلاف الإشارة$$ $ مضمنة $ T $ مضمنة ، أي$$ $ inline $ u (t- \ tau_n) ≈ u (t- \ tau_m) $ inline $ . وبالتالي ، يمكن كتابة شرط تماسك إشارة ضيقة النطاق على النحو التالي:

$$عرض $$ $ T≈ \ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = الحد الأقصى (\ tau_k- \ tau_m) $$ عرض $$

حيث$$ $ inline $ D_ {max} $ inline $ - الحد الأقصى للمسافة بين عناصر AR ، و$$ $ المضمنة مع $ المضمنة هي سرعة الضوء.

عند تلقي إشارة ، يتم إجراء الجمع المتماسك رقمياً في وحدة المعالجة المكانية. في هذه الحالة ، يتم تحديد القيمة المعقدة للإشارة الرقمية عند إخراج هذه الكتلة بالتعبير:

$$عرض $$ $$ y = \ sum_ {n = 1} ^ Nw_n ^ * x_n $$ عرض $$

من الأسهل تقديم التعبير الأخير في شكل منتج عددي للمتجهات المعقدة ذات الأبعاد N في صورة مصفوفة:

$$عرض $$ $$ y = (\ textbf {w} ، \ textbf {x}) = \ textbf {w} ^ H \ textbf {x} $$ عرض $$

حيث w و x متجهات العمود ، و$$ $ inline $ (.) ^ H $ inline $ - تشغيل الاقتران الهرمي .

يمثل تمثيل المتجهات للإشارات أحد العوامل الأساسية عند العمل مع صفائف الهوائي ، لأن غالبا ما يتجنب الحسابات الرياضية المرهقة. بالإضافة إلى ذلك ، غالبًا ما يتيح لنا تحديد إشارة يتم تلقيها في لحظة معينة من الزمن باستخدام ناقل ما من نظام مادي حقيقي وفهم ما يحدث بالضبط من وجهة نظر الهندسة.

من أجل حساب مخطط الاتجاهية لصفيف الهوائي ، من الضروري "تشغيل" عقليًا وثابتًا بمجموعة من موجات الطائرة من جميع الاتجاهات الممكنة. في هذه الحالة ، يمكن تمثيل قيم عناصر المتجه x على النحو التالي:

$$عرض $$ $$ x_n = s_n = \ exp \ {- i (\ textbf {k} (\ phi، \ theta)، \ textbf {r} _n) \} $$ عرض $$

حيث k هي متجه الموجة$$ $ inline $ \ phi $ inline $ و$$ $ inline $ \ theta $ inline $ - زاوية السمت وزاوية الارتفاع التي تحدد اتجاه وصول موجة مستوية ،$$ $ inline $ \ textbf {r} _n $ inline $ - تنسيق عنصر الهوائي ،$$ $ مضمنة $ s_n $ مضمنة $ - عنصر متجه التدريجي لموجة مستوية مع متجه الموجة k (في الأدب الإنجليزي ، يُسمى متجه التدريج متجه التوجيه). اعتماد مربع من سعة y على$$ $ inline $ \ phi $ inline $ و$$ $ inline $ \ theta $ inline $ يحدد مخطط الاتجاهية لصفيف الهوائي عند الاستقبال لمتجه معين لمعاملات الوزن w .

ملامح مجموعة الهوائي

من المريح دراسة الخصائص العامة لمخطط إشعاع صفيف الهوائي على صفيف هوائي خطي متساوي الطول في مستوي أفقي (أي أن مخطط الحزمة يعتمد فقط على زاوية السمت$$ $ inline $ \ phi $ inline $ ). أنها مريحة من وجهة نظر اثنين: الحسابات التحليلية والعرض البصري.

نحن نحسب DN لمتجه وحدة الوزن ($$ $ inline $ w_n = 1 ، n = 1 ... N $ مضمّن $ ) ، باتباع النهج الموضح أعلاه .


نتيجة لذلك ، نحصل على:

$$عرض $$ $ F (\ phi) = | y | ^ 2 = \ frac {\ sin ^ 2 (\ pi \ frac {Nd} {\ lambda} \ sin \ phi)} {\ sin ^ 2 (\ pi \ frac {d} {\ lambda} \ sin \ phi)} عرض $$ $

تردد نمط الإشعاع

مخطط الإشعاع الناتج عن صفيف الهوائي هو وظيفة دورية لجيب الزاوية. وهذا يعني أنه بالنسبة لقيم معينة من نسبة d / ، ، يكون الحد الأقصى (إضافي) للحيود.
مخطط الهوائي غير الطبيعي لـ N = 5
مخطط الإشعاع الطبيعي لمصفوفة الهوائي لـ N = 5 في نظام الإحداثيات القطبية

يمكن عرض موضع "الحيود" مباشرةً من صيغة NAM. ومع ذلك ، سنحاول أن نفهم من أين هم جسديًا وهندسيًا (في الفضاء ذي الأبعاد N).

عناصر متجه التدريجي هي الأسس المعقدة$$ $ inline $ e ^ {i \ Psi n} $ inline $ يتم تحديد قيمها بقيمة الزاوية المعممة$$ $ inline $ \ Psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi $ inline $ . إذا كان هناك زاويتان معممتان تقابلان اتجاهات مختلفة لوصول موجة طائرة ، والتي من أجلها$$ $ inline $ \ Psi_1 = \ Psi_2 + 2 \ pi m $ inline $ ، هذا يعني شيئين:

• جسديا: تحفز جبهات الموجة المستوية القادمة من هذه الاتجاهات توزيعات مماثلة لطور السعة للموجات الكهرمغنطيسية على عناصر صفيف الهوائي.
• هندسيًا: تتزامن المتجهات التدريجية لهاتين الاتجاهين.

اتجاهات وصول الموجة المتصلة بطريقة مماثلة مكافئة من وجهة نظر صفيف الهوائي ولا يمكن تمييزها عن بعضها البعض.

كيفية تحديد منطقة الزوايا التي يوجد بها دائمًا الحد الأقصى الرئيسي الوحيد للعنصر MD ؟ سنفعل ذلك على مقربة من السمت صفر للأسباب التالية: يجب أن يكمن تحول المرحلة بين عنصرين متجاورين في الفاصل الزمني من$$ $ inline $ - \ pi $ inline $ إلى$$ $ inline $ \ pi $ inline $ .

$$عرض $$ $$ - \ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $$ عرض $$

لحل هذا التباين ، نحصل على شرط في منطقة التفرد في حي يساوي صفرًا:

$$عرض $$ $$ | \ sin \ phi | <\ frac {\ lambda} {2d} $$ عرض $$

يمكن ملاحظة أن حجم منطقة التفرد في الزاوية يعتمد على نسبة d / λ . إذا كانت d = 0.5 λ ، يكون كل اتجاه لوصول الإشارة "فرديًا" ، وتغطي منطقة التفرد كامل نطاق الزوايا. إذا كانت d = 2.0 λ ، فيكون الاتجاهان 0 و ± 30 و ± 90 مكافئين. تظهر فصوص الحيود على نمط الإشعاع.

عادة ، تميل فصوص الحيود إلى قمعها باستخدام عناصر الهوائي الاتجاهي. في هذه الحالة ، فإن مخطط الإشعاع الكامل لصفيف الهوائي هو نتاج مخطط عنصر واحد ومجموعة عناصر متناحية الخواص. عادة ما يتم اختيار معلمات DN لعنصر واحد على أساس الحالة في منطقة التفرد لصفيف الهوائي.

عرض الفص الرئيسي

الصيغة الهندسية لتقدير عرض الفص الرئيسي لنظام الهوائي معروفة على نطاق واسع :$$ $ inline $ \ Delta \ phi ≈ \ frac {\ lambda} {D} $ inline $ حيث D هو الحجم المميز للهوائي. يتم استخدام الصيغة لأنواع مختلفة من الهوائيات ، بما في ذلك SLR منها. نظهر أنه صالح أيضًا لمصفوفات الهوائي.

نحدد عرض الفص الرئيسي بواسطة الأصفار الأولى من MD في محيط الحد الأقصى الرئيسي. البسط من التعبير ل$$ $ inline $ F (\ phi) $ inline $ تختفي في$$ $ inline $ \ sin \ phi = m \ frac {\ lambda} {dN} $ inline $ . تتوافق الأصفار الأولى مع m = ± 1. الاعتقاد$$ $ inline $ \ frac {\ lambda} {dN} << 1 $ inline $ نحن نحصل عليها$$ $ inline $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ inline $ .

عادة ، يتم تحديد عرض حزمة الاتجاهية AR بمستوى القدرة نصف (-3 ديسيبل). في هذه الحالة ، استخدم التعبير:

$$عرض $$ $$ \ Delta \ phi≈0.88 \ frac {\ lambda} {dN} $$ عرض $$

يمكن التحكم في عرض الفص الرئيسي عن طريق تحديد قيم مختلفة من السعات لمعاملات الوزن في صفيف الهوائي. فكر في ثلاث توزيعات:

• توزيع سعة موحدة (الأوزان 1):$$ $ مضمنة $ w_n = 1 $ مضمنة .
• قيم السقوط التي تقع على حواف شعرية (الأوزان 2):$$ $ inline $ w_n = 0.5 + 0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $
• زيادة قيم السعة إلى حواف المشبك (الأوزان 3):$$ $ inline $ w_n = 0.5-0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $

يوضح الشكل مخططات الإشعاع الطبيعية الناتجة على مقياس لوغاريتمي:
يمكن ملاحظة الاتجاهات التالية من الشكل: إن توزيع سعات معاملات الوزن التي تتناقص نحو حواف الشبكة يؤدي إلى توسيع الفص الرئيسي للعنبر ، ولكن إلى انخفاض في مستوى الفصوص الجانبية. تؤدي السعات المتزايدة باتجاه حواف صفيف الهوائي ، على العكس من ذلك ، إلى تضييق الفص الرئيسي وزيادة مستوى الجانبين. من المريح التفكير في الحد من الحالات هنا:

1. اتساع معاملات الترجيح لجميع العناصر باستثناء العناصر المتطرفة تساوي الصفر. الأوزان للعناصر المتطرفة تساوي وحدة. في هذه الحالة ، تصبح الشبكة مكافئة لعنصر AR مكون من فترة D = (N-1) d . ليس من الصعب تقدير عرض البتلة الرئيسي وفق الصيغة أعلاه. في هذه الحالة ، سوف تتحول الخطوط الجانبية إلى الحد الأقصى للحيود وتتماشى مع الحد الأقصى الرئيسي.
2. وزن العنصر المركزي يساوي واحد ، والباقي يساوي الصفر. في هذه الحالة ، لدينا أساسًا هوائي واحد به مخطط إشعاع متساوي التوتر.

اتجاه الحد الأقصى الرئيسي

لذلك ، نظرنا في كيفية ضبط عرض الفص الرئيسي لـ AP AR . الآن دعونا نرى كيفية توجيه الاتجاه. أذكر تعبير المتجه للإشارة المستقبلة. لنفترض أننا نريد أن ينظر مخطط الإشعاع الأقصى في اتجاه معين$$ $ inline $ \ phi_0 $ inline $ . هذا يعني أنه يجب أخذ أقصى طاقة من هذا الاتجاه. يتوافق المتجه التدريجي مع هذا الاتجاه$$ $ inline $ \ textbf {s} (\ phi_0) $ inline $ في فضاء متجه الأبعاد N ، يتم تعريف القدرة المستقبلة على أنها مربع للمنتج القياسي لهذا المتجه التدريجي بواسطة متجه معاملات الوزن w . يكون ناتج العددية الخاص بمتجهين هو الحد الأقصى عندما يكونان متصلان ، على سبيل المثال$$ $ inline $ \ textbf {w} = \ beta \ textbf {s} (\ phi_0) $ inline $ ، حيث β هو بعض عامل التطبيع. وبالتالي ، إذا اخترنا متجهًا للوزن مساوًا لمتجه التدريج للاتجاه المطلوب ، فسنقوم بتدوير مخطط الإشعاع الأقصى.

النظر في الأوزان التالية كمثال:$$ $ inline $ \ textbf {w} = \ textbf {s} (10 °) $ inline $

$$عرض $$ $$ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda} (n-1) \ sin (10 \ pi / 180) \} $$ عرض $$

نتيجة لذلك ، نحصل على مخطط إشعاع مع الحد الأقصى الرئيسي في اتجاه 10 درجة.

الآن نطبق نفس الأوزان ، ولكن ليس لاستقبال الإشارة ، ولكن للإرسال. هنا تجدر الإشارة إلى أنه عند إرسال إشارة ، يتم عكس اتجاه متجه الموجة. هذا يعني أن عناصر متجه التدريج للاستقبال والإرسال تختلف في تسجيل الدخول في الأس ، أي مترابطة بواسطة الاقتران المعقدة. ونتيجة لذلك ، نحصل على الحد الأقصى لمخطط الإشعاع في اتجاه -10 درجة ، والذي لا يتزامن مع الحد الأقصى لإشارة الاستقبال في معاملات الوزن نفسها ، لتصحيح الموقف ، من الضروري تطبيق الاقتران المعقد أيضًا على معاملات الوزن.

يجب دائمًا مراعاة الميزة الموضحة في تشكيل الحزم للاستقبال والإرسال عند العمل مع صفائف الهوائي.

هيا نلعب مع نمط الإشعاع

ارتفاعات قليلة

نطرح المشكلة لتشكيل اثنين من الحدود القصوى لنمط الإشعاع في الاتجاه: -5 ° و 10 °. للقيام بذلك ، نختار المبلغ الموزون للمتجهات التدريجية للاتجاهات المقابلة كمتجه للوزن.

$$عرض $$ $$ \ textbf {w} = \ beta \ textbf {s} (10 °) + (1- \ beta) \ textbf {s} (- 5 °) عرض $$ $$

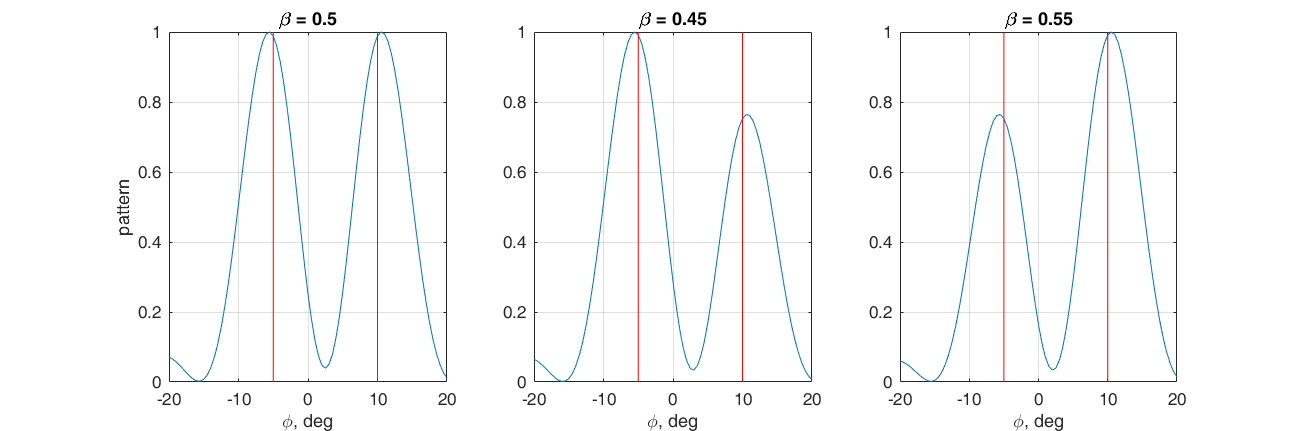
عن طريق ضبط المعامل β ، يمكن ضبط النسبة بين الفصوص الرئيسية. هنا مرة أخرى ، من المريح النظر إلى ما يحدث في الفضاء المتجه. إذا كانت greater أكبر من 0.5 ، فإن متجه الأوزان يقع بالقرب من s (10 °) ، وإلا s (-5 °). كلما اقتربت ناقلات الوزن من أحد الأطوار ، زاد عدد المنتجات العددية المقابلة ، وبالتالي حجم الحد الأقصى المقابل من ND .

ومع ذلك ، تجدر الإشارة إلى أن كل من بتلات الرئيسية لها عرض محدود ، وإذا كنا نريد أن نضبط في اتجاهين وثيقين ، ثم سيتم دمج هذه بتلات في واحدة ، موجهة إلى بعض الاتجاه الأوسط.

واحد كحد أقصى والصفر

الآن دعونا نحاول ضبط الحد الأقصى لنمط الإشعاع على الاتجاه$$ $ inline $ \ phi_1 = 10 ° $ inline $ وقمع في وقت واحد إشارة قادمة من الاتجاه$$ $ inline $ \ phi_2 = -5 ° $ inline $ . لهذا ، من الضروري تعيين الصفر للزاوية المقابلة. يمكنك القيام بذلك على النحو التالي:

$$عرض $$ $$ \ textbf {w} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf {s} _2 $$ عرض $$

حيث$$ $ inline $ \ textbf {s} _1 = \ textbf {s} (10 °) $ inline $ و$$ $ inline $ \ textbf {s} _2 = \ textbf {s} (- 5 °) $ inline $ .

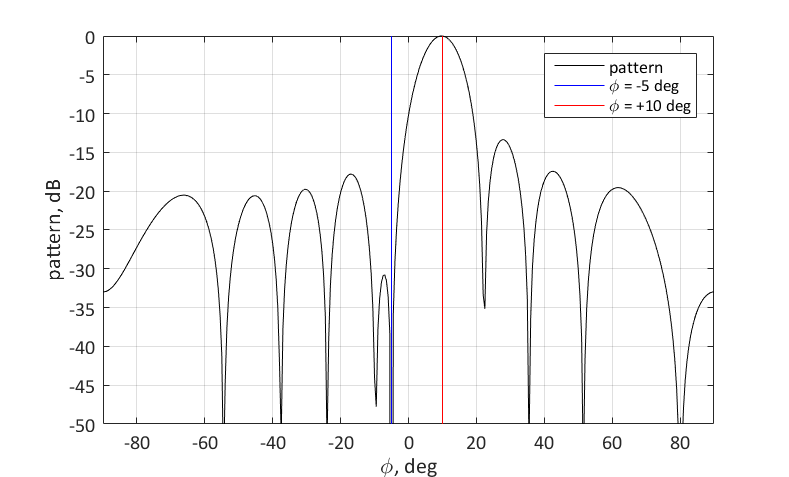
المعنى الهندسي لاختيار متجه الوزن هو على النحو التالي. نريد أن يكون لهذا المتجه w أقصى إسقاط عليه$$ $ inline $ \ textbf {s} _1 $ inline $ وكان متعامدا للناقل$$ $ inline $ \ textbf {s} _2 $ inline $ . سهم التوجيه$$ $ inline $ \ textbf {s} _1 $ inline $ يمكن تمثيله كمصطلحين: متجه خطي$$ $ inline $ \ textbf {s} _2 $ inline $ والناقل المتعامد$$ $ inline $ \ textbf {s} _2 $ inline $ . لتلبية بيان المشكلة ، من الضروري اختيار المكون الثاني كمتجه لمعاملات الوزن w . يمكن حساب المكون الخطي من خلال تصميم ناقل$$ $ inline $ \ textbf {s} _1 $ inline $ لمتجه تطبيع$$ $ inline $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ inline $ باستخدام منتج العددية.

$$عرض $$ $$ \ textbf {s} _ {1 ||} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {\ sqrt {N}} $$ عرض $$

وفقا لذلك ، طرح من ناقلات مراحل الأولية$$ $ inline $ \ textbf {s} _1 $ inline $ مكونها الخطي ، نحصل على ناقلات الوزن المطلوبة.

بعض الملاحظات الإضافية

1. في كل مكان أعلاه ، قمت بحذف مسألة تطبيع ناقلات الوزن ، أي طوله. لذلك ، لا يؤثر تطبيع متجه الوزن على خصائص مخطط إشعاع صفيف الهوائي: اتجاه الحد الأقصى الرئيسي ، عرض الفص الرئيسي ، إلخ. يمكن أيضًا توضيح أن هذا التطبيع لا يؤثر على SNR عند إخراج كتلة المعالجة المكانية. في هذا الصدد ، عند التفكير في خوارزميات معالجة الإشارات المكانية ، عادة ما أقبل تطبيع الوحدة لمتجه الوزن ، أي$$ $ inline $ \ textbf {w} ^ H \ textbf {w} = 1 $ inline $
2. يتم تحديد إمكانات تشكيل قاع صفيف الهوائي بعدد العناصر N. وكلما زاد عدد العناصر كلما زادت الإمكانيات. لمزيد من درجات الحرية في تنفيذ معالجة الوزن المكاني ، والمزيد من الخيارات لكيفية "تحريف" ناقلات الوزن في الفضاء N- الأبعاد.
3. عند استقبال مخطط حزمة الهوائي ، لا توجد صفيف الهوائي ماديًا ، وكل هذا موجود فقط في "خيال" وحدة الحوسبة التي تعالج الإشارة. هذا يعني أنه في الوقت نفسه ، من الممكن تجميع العديد من MDs ومعالجة الإشارات القادمة من اتجاهات مختلفة بشكل مستقل. في حالة الإرسال ، يكون كل شيء أكثر تعقيدًا إلى حد ما ، ولكن من الممكن أيضًا تجميع العديد من MDs لنقل تدفقات البيانات المختلفة. وتسمى هذه التكنولوجيا في أنظمة الاتصالات MIMO .
4. باستخدام كود ماتلاب المقدم ، يمكنك اللعب مع NAM بنفسك
   
   قانون

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

ما المهام التي يمكن حلها بمساعدة مجموعة الهوائي التكيفي؟

شكرا لاهتمامكم