هذه ترجمة لمقال إليعازر يودكوفسكي من دورة علمية شهيرة مكرسة للتفسير متعدد المتغيرات لميكانيكا الكم. تمت ترجمة بداية الدورة إلى محور ، ولكن يبدو أن المترجم قد تعب. يمكن فهمه - المواد ضخمة جدًا. Yudkovsky يحب نشر الفكر على الشجرة. من ناحية أخرى ، فإن المادة معقدة حقًا ، وتكرار نفس الشيء بكلمات مختلفة يتيح للصورة في رأس قارئ غير مستعد للاحتفاظ بها بطريقة ما على الأقل. لن أتعهد بمواصلة ترجمة الدورة بأكملها ، لكنني سأحاول ترجمة اثنين من أهم المقالات.

سوف أتخطى المقالات في السلسلة حول مسافات الحالة ( الكلاسيكية والكمية ) - يتم استخدام المفهوم كثيرًا حيث يجب أن يكون مألوفًا بالنسبة للقارئ المدربين تقنيًا. وتخطي أيضًا تكاملات مسار Feynman - يمكن العثور عليها في مصدر العلوم الشهير الممتاز.

لكن المنشور التالي يجيب على سؤال مهم. إذا كان العالم "الحقيقي" على المستوى الأساسي هو الكم ، حيث يتم الخلط بين كل شيء وكل شيء يؤثر على بعضها البعض ، من أين تأتي النظم الكلاسيكية؟ لماذا نرى الظواهر الكمومية "الطبيعية" نادراً جداً في الحياة العادية؟ هذا ما يسميه المؤلف "هلوسة كلاسيكية". لماذا ، على سبيل المثال ، يحتاج مبدعو الحواسيب الكمومية إلى بذل هذه الجهود الهائلة للحفاظ على النظام في حالة "طبيعية" متشابكة؟

إخلاء المسئولية: أنا لست فيزيائيًا محترفًا ولا مترجمًا محترفًا (وكذلك مؤلف الأصل).

فك الترابط

لفهم عملية كمية تسمى decoherence ، عليك أولاً أن تفهم كيف يتم تدمير حالة خاصة من الاستقلال الكمومي ، أي كيف ينتقل بالضبط النظام الكمي من حالة الاستقلال إلى حالة التشابك.

استقلال الكم ، كما نذكر ، هو حالة "مستطيلة" خاصة لتوزيع السعة ومعالجتها جيدًا. أي أنه يمكن تمثيله كمنتج لتوزيعات الأجزاء المكونة للنظام ، والتي تبدو بالنسبة لنا "جزيئات منفصلة".

يأخذ السياح الخجولون الذين يزورون عالمنا الكمومي في بعض الأحيان غياب هذا التوزيع "المستطيل" لبعض الروابط الغامضة الخاصة بين الجزيئات. ومن هنا جاءت العبارة المؤسفة "التشابك الكمومي". في الواقع ، فإن أي تطور لنظام الكم عادة يولد التشابك من الاستقلال (وليس العكس) ، وتحويل توزيعات مستطيلة إلى غير مستطيلة. الاستقلال نادر وسهل التدمير.

لفهم أفضل للعمليات المادية التي تؤدي إلى التشابك ، نبدأ بالنظام الكلاسيكي. يوضح الشكل نظام كرة خفيفة مشحونة إيجابياً على المسار العلوي وكره ثقيلة سالبة الشحنة على المسار السفلي. في البداية ، كرتان متباعدتان وتقريباً لا تتفاعلان. ثم نخفض المسار العلوي ، ونجمع الكرات معًا حتى تبدأ في جذب بعضها البعض (يتم جذب الشحنات المعاكسة). وتتدحرج الكرة الخفيفة إلى كرة ثقيلة (والكرة الثقيلة تدحرج قليلاً إلى كرة خفيفة ، تمامًا كما تجذب التفاحة الساقطة الأرض قليلاً إلى نفسها).

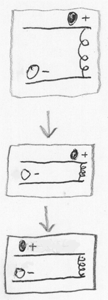
الآن دعنا ننظر إلى هذا النظام كنظام كمومي ، من وجهة نظر تكامل مسار فاينمان . أي أننا نمثل تطور النظام كمجموع لكل المسارات الممكنة من الحالة الأولية في مساحة التكوين. لنفترض أن الكرتين مستقلتان في البداية عن الكم ، يمكن تمثيل التوزيع المشترك للاتساعات كمنتج "توزيع للكرة السفلية" و "توزيع للكرة العليا".

علاوة على ذلك ، دع سعة الكرة السفلية في البداية تتكون من ثلاثة أجزاء (والتي من وجهة نظر Feynman integrals يمكن اعتبارها ثلاث حالات أولية). عندما نخفض المسار العلوي ، يجب سحب الكرة العلوية إلى المستوى السفلي. ولكن إذا كانت السعة المشتركة للكرة السفلية تتكون من عدة أجزاء ، في النهاية سنحصل على توزيع مشترك يتكون من عدة أجزاء ، يصف كل منها الموضع الجديد للكرات.

أبذل قصارى جهدي لتجنب العبارات مثل "يمكن أن تكون الكرة السفلية في واحد من ثلاثة أماكن" أو "في كل حالة ممكنة ، تنجذب الكرة العليا إلى الموضع المقابل لها". على الرغم من أنك ربما لا تزال تتخيل كل شيء بهذه الطريقة. في النهاية ، أنا شخصياً أوضحت ذلك. وجهت ثلاث وظائف بداية ممكنة وثلاثة نتائج ممكنة. ما يجب القيام به ، يتخيل الدماغ البشري عادة تكاملات فاينمان. لكن هذا لا يعني أن هناك ثلاث حالات ممكنة للكون . هذه مجرد خدعة لتصور المسار لا يتجزأ. جميع مكونات السعة الثلاثة موجودة في عالمنا ، والمكونات الثلاثة جميعها حقيقية على قدم المساواة ، ولكنها ليست ممكنة أو محتملة على الإطلاق.

الآن تخيل أنه في البداية يتم "تلطيخ" سعة الكرة السفلية على المسار بالكامل. لا تزال سعة الكرة العلوية مركزة في مكان واحد. بعد ذلك ، سيكون التوزيع المشترك في البداية على شكل مستطيل ممدود ، ثم يتحول إلى قطري.

على المحور X يوجد موضع الكرة العليا ، على المحور Y - القاع. نبدأ مع كرة موضعية بدقة وكره سفلية "غير واضحة" وننتهي بتوزيع مترابط عندما يكون كلا الإحداثيين غير واضحين لكن متساويين مع بعضهما البعض (مبسط). وهذا يعني أن التوزيع القابل للعوامل في البداية تحول إلى "نظام مربك" - لم يعد يتحلل إلى عاملين مستقلين.

(ملاحظة مهمة:

لاحظ أنه في الشكل أعلاه ، يطور تطوير النظام القانون الثاني للديناميكا الحرارية ، المعروف أيضًا باسم نظرية ليوفيل. عندما يتغير النظام ، يتم الحفاظ على "حجم السحابة" ، أي الحجم الكلي للسعة ، أو ببساطة أكثر ، حجم المنطقة الرمادية على الرسم البياني . إذا كان هناك في البداية في الشكل مربع رمادي فاتح ضخم (عندما يتم تشويه كلا الجسيمين بقوة في الفضاء) ، ثم وفقًا للقانون الثاني للديناميكا الحرارية ، لا يمكن أن يتحول إلى قطري رمادي غامق. للدخول في حالة تشابك ، يجب أن يكون للنظام في البداية انتروبيا منخفضة ، ويجب ألا تزيد هذه الإنتروبيا كثيرًا في هذه العملية.

اسمحوا لي أن أذكركم بأن المعلومات المتبادلة هي إنتروبيا مع الإشارة المعاكسة . السعات الكمية ليست معلومات بالكامل ، ولكن المبدأ هو نفسه. يجب أن تتركز السعة الأولية بما يكفي لإنتاج خط قطري مضغوط ، بدلاً من سحابة نادرة كبيرة. إذا تخيلنا أن توزيع السعة يحتوي على "إنتروب الكم" ، فينبغي أن تكون إنتروب النظام المتشابك منخفضة نسبيًا)

أخيرًا ، نحن مستعدون للحديث عن فك الارتباط.

النظام في الشكل معقد للغاية. يمكن وصف شيء من هذا القبيل: "هناك جزيئات ، وكلاهما يمكن أن يكون إما هنا أو هناك ." نعم ، قمت بصياغتها كما لو أن هناك حالتان محتملتان ، وليس توزيعًا حقيقيًا فعليًا للسعة. على محمل الجد ، لا أعرف كيف أصف فيزياء الكم بلغة عادية بطريقة عادية! فقط تذكر القاعدة العامة أن "الفرصة" أو "الاحتمال" هي اختصار لـ "امتداد توزيع السعة الموجود فعليًا". ثم يمكنني وصف السعات أقصر بكثير باستخدام مصطلحات عدم اليقين. ولكن تذكر أن هذا مجرد اتفاقية ! "الجسيم إما هنا أو هناك" يعني "توزيع موجود فعليًا لسعة جزأين ، واحد هنا ، والآخر هناك" ، وليس "الجسيم موجود في أحد المكانين ، لكننا لا نعرف أي واحد".

هكذا. عادةً ما يكون العمل مع الأنظمة المعقدة أمرًا صعبًا (بالنسبة للفيزيائيين ، بالطبع ، ليس للكون). أولاً ، يجب علينا حساب جميع المسارات الممكنة لجميع الشروط الأولية الممكنة (أي ، مراعاة جميع مسارات السعة الموجودة فعليًا في نظام فاينمان المتكامل). علاوة على ذلك ، من الضروري مراعاة تأثير هذه المسارات على بعضها البعض (لا يمكن أن تتفاعل المسارات المحتملة بالمعنى الدقيق للكلمة - فقط شيء موجود بالفعل يمكن أن يؤثر على شيء آخر). على سبيل المثال ، تلتقي جزيئاتنا مع 20 عنصرًا آخر ، تتفاعل بطريقة ما ، ونتيجة لذلك ، نحصل على مجموعة من التكوينات التي تأثرت بجميع النقاط السابقة لجميع الحالات الممكنة.

لاحظ أن التشابك يحدث فقط إذا كانت أقسام السعة الأولية قريبة من بعضها البعض. بحيث تتقاطع مسارات التنمية الخاصة بهم. إذا كان هناك جسيمان إما هنا أو هناك ، ولكن "هنا" و "هناك" مفصولة بمسافة سنتين ضوئيتين ، فإن مساراتها الإضافية يمكن أن تتقاطع في موعد لا يتجاوز عام واحد.

الآن إضافة الجسيم الثالث . يوضح الشكل مساحة تكوين ثلاثية الأبعاد ، تتحلل إلى فراغات فرعية ثنائية الأبعاد مستقلة أحادية البعد. وهذا هو ، جزيئات متشابكة واحدة مستقلة عنهم.

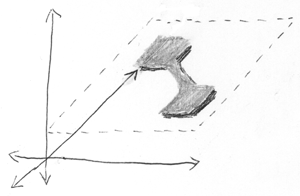
الارتفاع هو الجسيم الثالث ، العرض والعمق هما جزيئات متشابكة.

يوجد جسيم مستقل في مكان معين - التوزيع العمودي ضيق للغاية. يوجد جزيءان متشابكان إما هنا أو هناك (أستخدم مرة أخرى مصطلحات احتمالية غير صحيحة ، مثل "معينة" و "إما" ، لكنك تفهم ما أقصده).

تخيل الآن أن الجسيم الثالث يتفاعل مع اثنين متشابكين بطريقة حساسة لموقفهم. على سبيل المثال ، يوازن الجسيم الثالث في ذروة حادة ، جسيمان يطيران ، يجذبهان ، ويسقطان إما بطريقة أو بأخرى. بعد ذلك ، تبدو السعة مثل هذا.

الجسيم الثالث مرتبك الآن مع الاثنين الأخريين. وتتكون السعة الآن من قطعتين مفصولتين عن بعضهما البعض . وصف مبسط: "إذا كان هناك جسيمان هنا ، عندها يطير الجسيم الثالث هنا . وإذا كانوا هناك ، ثم طارت هناك ". وهذا يعني أن السعة أصبحت مشوشة تماما. لم يعد يتحلل إلى مساحات فرعية مستقلة.

لكن قطعتين من السعة أصبحتا الآن متباعدتين ، ويتألف كل منهما من ثلاث جسيمات في المنطقة المقابلة. حدث هذا لأن الجسيم الثالث حساس لتنسيق الآخرين. بعد التدحرج من ذروة حادة إلى أحد الجانبين ، تكون المسافة بين الإحداثيات النهائية كبيرة جدًا.

في الواقع ، فإن التدحرج من الأعلى اختياري. كل شيء يعمل بالطريقة نفسها إذا كان لديك عشرين جسيمًا تتفاعل مع الأولين وتختلط بينهما. سيبدو التوزيع النهائي في الفضاء ذي الأبعاد 22 كمنطقتين ، كل منهما يقابل 22 جسيمًا. وستكون المسافة بين هذه المناطق هائلة. وكلما زادت المسافة ، قل احتمال تأثير المناطق في المستقبل على بعضها البعض.
هذا هو فك الارتباط. هذا هو السبب الثالث "للهلوسة الكلاسيكية" ، لأن المنطقتين تبدأ بالتطور بشكل مستقل. هذا يسمح لهم بأن يوصفوا بأنظمة غير معقدة. بمجرد أن نفكر فيها بشكل منفصل ، يبدو التوزيع في كل منها "مستطيلًا" وبشكل مستقل في ثلاثة إحداثيات (حاولت إظهار ذلك في الشكل أعلاه).

في الكمبيوتر الكمومي ، من الصعب جدًا منع التراجع. تتطلب الحوسبة الكمية أن تظل أقسام السعة قريبة من بعضها البعض ويمكن أن تتفاعل. ولكن هناك تريليونات من الجسيمات الأخرى حولها التي تحاول باستمرار أن تتفاعل عن غير قصد مع عيوبنا الهشة ، مما يدمر السعة التي تم بناؤها بدقة.

ولا يمكنك فقط أخذ التالفة واستعادتها. للقيام بذلك ، من الضروري العودة إلى المكان كل الجسيمات المتفاعلة ، بما في ذلك الجسيمات العشوائية من البيئة (لا تنس أن السعة النهائية لها توزيع مشترك معهم).

(يبدو الأمر وكأنه عملية لا رجعة فيها تقريبًا ، أليس كذلك؟ إنها محاولة لجمع بيضة مكسورة مرة أخرى في القشرة. في الواقع ، هذا تشبيه جيد.

ولهذا السبب أكدت في وقت سابق أن عملية التشابك تبدأ بانخفاض في مستوى الكون. فك الارتباط لا رجعة فيه لأنه في الأساس عملية ديناميكية حرارية.

ينص أحد المبادئ المادية الأساسية على أنه يمكنك "إعادة عرض الفيلم" دون انتهاك القوانين الأساسية. إذا قمت بتصوير بيضة تتساقط على الأرض ثم تدحرجتها للخلف ، بحيث تحلق بيضة مكسورة من الأرض ، وتجمع مرة أخرى إلى قشرة ناعمة ، فلن ترى أي قانون جسدي منتهكًا. جميع الجزيئات ستكون ببساطة في المكان المناسب في الوقت المناسب ، وسوف ترتد البيضة عن الأرض بشكل آمن وسليم. هذا ليس مستحيلا ، من غير المرجح للغاية.

الأمر نفسه ينطبق على السعة المقطوعة إلى قطع نائية ، والعودة بشكل غير متوقع إلى حالة متماسكة - وهذا ممكن نظريًا. ولكن ليس هناك أي فرصة عملياً أن تكون القطع التي تم قطع اتصالها في البداية فجأة بجوار بعضها البعض. عملية العكس هو أكثر احتمالا.

في الواقع ، بالإضافة إلى التمرير الخلفي للفيلم ، فأنت بحاجة أيضًا إلى عكس رسوم جميع الجسيمات ، بالإضافة إلى تبديل اليسار واليمين (أو أحد البعدين الآخرين) ، وتحويل الكون إلى صورة معكوسة. تُعرف هذه القاعدة باسم "ثبات CPT" من الكلمات Charge و Parity و Time.

على الأرجح ، إن ثبات CPT هو أحد المبادئ الأساسية لتشغيل الكون. بالنسبة للفيزيائيين ، تبدو محاولات كسرها عبثية مثل محاولة رمي كرة أسرع من سرعة الضوء. حسب علمي ، فإن ثبات CPT ضروري لتناسق نظرية الحقل الكمومي.

لذلك ، فإن فك الترابط لا يبدو إلا كعملية أحادية الاتجاه ، ولكن في الواقع لا رجعة فيه ديناميكية حرارية وليست أساسية. وهذا مهم للغاية ، لأنه يستنتج من ذلك أن فيزياء الكم تراقب ثبات CPT.

بقدر ما نعلم ، فإن كل العمليات أحادية الاتجاه في الطبيعة هي نتيجة للقانون الثاني للديناميكا الحرارية ، وليس التباين الأساسي للوقت.)

لتلخيص. Decoherence هي عملية ديناميكية حرارية للتشابك الكمي المتزايد باستمرار ، والتي يتم إخفاءها بشكل مدهش كعملية لتدمير هذا التشابك نفسه. لا تتفاعل المناطق غير المتجانسة مع بعضها ، ويصبح كل منها أقل إرباكًا . Decoherence هو السبب الثالث لـ "الهلوسة الكلاسيكية". إنها تتيح للفيزيائيين اعتبار كل حقل مستقلًا ، دون الأخذ في الاعتبار الاحتمال الضئيل لتفاعلهم. بالإضافة إلى ذلك ، يصبح كل منطقة فردية أسهل للفهم من الداخل . هذا مفيد للغاية إذا كنت ترغب في حل المشاكل من حيث الفيزياء الكلاسيكية البسيطة. وهو غير مناسب للغاية إذا كنت ترغب في معالجة رقم مكون من مليون رقم قبل أن تغيب الشمس.