فهم خوارزمية FFT

مرحبا اصدقاء تبدأ دورة " خوارزميات للمطورين" غدًا ، ولا يزال لدينا ترجمة واحدة غير منشورة. في الواقع نحن نصحح ونشارك المواد معك. دعنا نذهب.

يعد تحويل فورييه السريع (FFT) أحد أهم خوارزميات معالجة الإشارات وتحليل البيانات. لقد استخدمتها لسنوات دون معرفة رسمية في علوم الكمبيوتر. ولكن هذا الأسبوع حدث لي أنني لم أتساءل أبدًا كيف يحسب FFT تحويل فورييه المنفصل بهذه السرعة. لقد تخلصت من الغبار من كتاب قديم عن الخوارزميات ، وفتحته ، وقرأت بسرور عن الخدعة الحسابية البسيطة المخادعة التي وصفها J.V Cooley و John Tukey في عملهما الكلاسيكي لعام 1965 حول هذا الموضوع.



الهدف من هذا المنشور هو الانغماس في خوارزمية Cooley-Tukey FFT ، وشرح التماثلات التي تؤدي إليها ، وإظهار بعض تطبيقات Python البسيطة التي تطبق النظرية في الممارسة العملية. آمل أن تقدم هذه الدراسة للمتخصصين في تحليل البيانات ، مثلي ، صورة أكثر اكتمالًا لما يحدث تحت غطاء الخوارزميات التي نستخدمها.

تحويل فورييه المنفصل

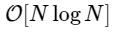
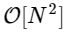
FFT سريع خوارزمية لحساب تحويل فورييه المنفصل (DFT) ، والذي يتم حسابه مباشرة من أجل . يحتوي DFT ، مثل الإصدار المستمر الأكثر دراية من تحويل فورييه ، على شكل مباشر وعكسي ، يتم تعريفه على النحو التالي:

تحويل فورييه المنفصل المباشر (DFT):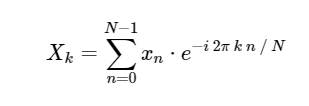



تحويل فورييه المنفصل (ODPF):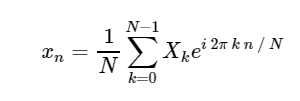



التحويل من xn → Xk هو ترجمة من مساحة التكوين إلى مساحة التردد ويمكن أن يكون مفيدًا للغاية لدراسة طيف قدرة الإشارة ولتحويل مهام معينة من أجل حساب أكثر كفاءة. يمكنك العثور على بعض الأمثلة على ذلك في الفصل 10 من كتابنا المستقبلي عن علم الفلك والإحصاء ، حيث يمكنك أيضًا العثور على الصور ورمز مصدر Python. للحصول على مثال على استخدام FFT لتبسيط تكامل المعادلات التفاضلية المعقدة ، راجع مشاركتي "حل معادلة Schrödinger في Python" .

نظرًا لأهمية FFT (المشار إليها فيما يلي ، يمكن استخدام FFT - Fast Fourier Transform) في العديد من مناطق Python على العديد من الأدوات والقذائف القياسية لحسابها. يحتوي كل من NumPy و SciPy على قذائف من مكتبة FFTPACK المختبرة جيدًا والموجودة في scipy.fftpack و scipy.fftpack على التوالي. أسرع FFT التي أعرفها موجودة في حزمة FFTW ، والتي تتوفر أيضًا في Python من خلال حزمة PyFFTW .

ولكن في الوقت الحالي ، دعنا نترك هذه التطبيقات جانباً ونتساءل كيف يمكننا حساب FFT في بيثون من نقطة الصفر.

حساب تحويل فورييه المنفصل

للبساطة ، سوف نتعامل فقط مع التحويل المباشر ، حيث يمكن تنفيذ التحول العكسي بطريقة مشابهة للغاية. بالنظر إلى التعبير أعلاه لـ DFT ، نرى أن هذا ليس أكثر من عملية خطية واضحة: ضرب المصفوفة بواسطة متجه





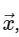
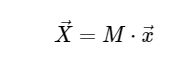
مع مصفوفة M معين



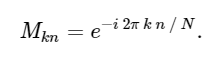
مع وضع ذلك في الاعتبار ، يمكننا حساب DFT باستخدام الضرب البسيط للمصفوفة على النحو التالي:

في [1]:

 import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x) 

يمكننا التحقق من النتيجة بمقارنتها مع وظيفة FFT المدمجة في numpy:

في [2]:

 x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x)) 

0ut [2]:

True

فقط لتأكيد بطء خوارزمية لدينا ، يمكننا مقارنة وقت تنفيذ هذين النهجين:

في [3]:

 %timeit DFT_slow(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop 

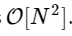
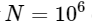
نحن أبطأ من 1000 مرة ، وهو أمر متوقع لهذا التنفيذ المبسط. ولكن هذا ليس هو الأسوأ. بالنسبة لمتجه المدخلات ذات الطول N ، يتم حساب خوارزمية FFT كـ بينما لدينا الخوارزمية بطيئة جداول مثل . هذا يعني أن ل عناصر ، نتوقع أن تكتمل FFT في حوالي 50 مللي ثانية ، بينما ستستغرق الخوارزمية البطيئة لدينا حوالي 20 ساعة!

فكيف تحقق FFT مثل هذا التسارع؟ الجواب هو استخدام التماثل.

التماثلات في تحويل فورييه المنفصل

واحدة من أهم الأدوات في بناء الخوارزميات هو استخدام تماثل المهام. إذا أمكنك إظهار تحليلي أن جزءًا من المشكلة يرتبط ببساطة بالآخر ، يمكنك حساب النتيجة الفرعية مرة واحدة فقط وحفظ هذه التكلفة الحسابية. استخدم Cooley and Tukey هذا النهج بالضبط للحصول على FFT.
نبدأ بسؤال المعنى . من تعبيرنا أعلاه:



حيث استخدمنا هوية exp [2π in] = 1 ، والتي تحمل أي عدد صحيح n.

يظهر السطر الأخير جيدًا خاصية التناظر الخاصة بـ DFT:



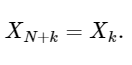
امتداد بسيط



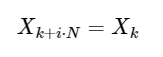
عن أي عدد صحيح ط. كما سنرى أدناه ، يمكن استخدام هذا التناظر لحساب DFT بشكل أسرع بكثير.

DFT في FFT: باستخدام التماثل

أظهر Cooley و Tukey أنه يمكن تقسيم حسابات FFT إلى قسمين أصغر. من تعريف DFT لدينا:



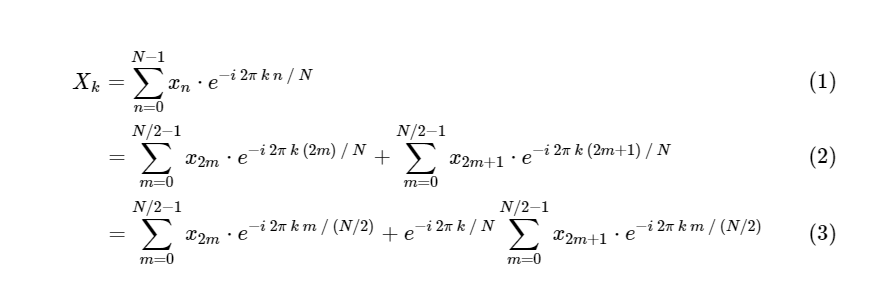
لقد قسمنا تحويل فورييه المنفصل إلى فترتين ، والتي في حد ذاتها تشبه إلى حد كبير تحويلات فورييه المنفصلة الأصغر ، واحدة إلى قيم برقم فردي وواحد إلى قيم برقم زوجي. ومع ذلك ، لم نحفظ حتى الآن أي دورات حسابية. يتكون كل مصطلح من (N / 2) ∗ N حسابات ، المجموع .

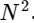
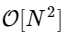
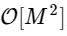
الحيلة هي استخدام التماثل في كل من هذه الشروط. نظرًا لأن نطاق k هو 0≤k <N ، ومدى n هو 0≤n <M≡N / 2 ، نرى من خصائص التناظر أعلاه أننا بحاجة إلى إجراء نصف الحسابات فقط لكل مهمة فرعية. حسابنا أصبح حيث M أقل مرتين من N.

ولكن لا يوجد سبب للتفكير في هذا: ما دامت لدينا تحويلات فورييه الأصغر حجماً لها M متساوية ، فيمكننا إعادة تطبيق هذا النهج للتغلب على الفجوة وقهر ، في كل مرة خفض التكلفة الحسابية إلى النصف ، حتى تصبح صفائفنا صغيرة بما فيه الكفاية بحيث لم تعد الاستراتيجية تستفيد. في الحد المقارب ، هذا المقياس العودية يحكم O [NlogN].

يمكن تنفيذ هذه الخوارزمية العودية بسرعة كبيرة في Python ، بدءًا من رمز DFT البطيء ، عندما يصبح حجم المهمة الفرعية صغيرًا جدًا:

في [4]:

 def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32: # this cutoff should be optimized return DFT_slow(x) else: X_even = FFT(x[::2]) X_odd = FFT(x[1::2]) factor = np.exp(-2j * np.pi * np.arange(N) / N) return np.concatenate([X_even + factor[:N / 2] * X_odd, X_even + factor[N / 2:] * X_odd]) 

سنقوم هنا بفحص سريع لأن الخوارزمية لدينا تعطي النتيجة الصحيحة:
في [5]:

 x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x)) 

خارج [5]:
True

قارن هذه الخوارزمية بإصدارنا البطيء:
في [6]:

 %timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop 

حسابنا أسرع من الإصدار المباشر! علاوة على ذلك ، خوارزمية العودية لدينا هي متناظرة : قمنا بتنفيذ تحويل فورييه السريع.

لاحظ أننا ما زلنا لا نقترب من سرعة خوارزمية FFT المدمجة المضمنة ، ويجب توقع ذلك. خوارزمية FFTPACK وراء fft numpy هي تطبيق Fortran الذي تلقى سنوات من التحسين والتحسين. بالإضافة إلى ذلك ، يتضمن حل NumPy الخاص بنا كلا من تكرار مكدس Python وتخصيص العديد من الصفائف المؤقتة ، مما يزيد من الوقت الحسابي.

تتمثل الإستراتيجية الجيدة لتسريع الكود عند العمل مع Python / NumPy في توجيه العمليات الحسابية المتكررة كلما أمكن ذلك. يمكننا القيام بذلك - في هذه العملية ، نقوم بحذف استدعاءات الوظائف المتكررة ، مما سيجعل Python FFT لدينا أكثر فاعلية.

المتجهات نسخة Numpy

يرجى ملاحظة أنه في التنفيذ المتكرر أعلاه لـ FFT ، عند أدنى مستوى من العودية ، نقوم بإجراء منتجات متجهية مصفوفة متطابقة N / 32 . ستفوز فعالية الخوارزمية الخاصة بنا إذا قمنا بحساب هذه المنتجات في نفس الوقت كمتجه مصفوفة واحد. في كل مستوى من مستويات التكرار اللاحقة ، نقوم أيضًا بإجراء عمليات متكررة يمكن توجيهها. يقوم NumPy بعمل ممتاز في مثل هذه العملية ، ويمكننا استخدام هذه الحقيقة لإنشاء هذه النسخة الموجهة من تحويل فورييه السريع:

في [7]:

 def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2") # N_min here is equivalent to the stopping condition above, # and should be a power of 2 N_min = min(N, 32) # Perform an O[N^2] DFT on all length-N_min sub-problems at once n = np.arange(N_min) k = n[:, None] M = np.exp(-2j * np.pi * n * k / N_min) X = np.dot(M, x.reshape((N_min, -1))) # build-up each level of the recursive calculation all at once while X.shape[0] < N: X_even = X[:, :X.shape[1] / 2] X_odd = X[:, X.shape[1] / 2:] factor = np.exp(-1j * np.pi * np.arange(X.shape[0]) / X.shape[0])[:, None] X = np.vstack([X_even + factor * X_odd, X_even - factor * X_odd]) return X.ravel() 

على الرغم من أن الخوارزمية أكثر عتامة قليلاً ، إلا أنها مجرد إعادة ترتيب للعمليات المستخدمة في النسخة العودية ، مع استثناء واحد: نستخدم التماثل في حساب المعاملات وننشئ نصف الصفيف فقط. مرة أخرى ، نؤكد أن وظيفتنا تعطي النتيجة الصحيحة:

في [8]:

 x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x)) 

خارج [8]:
True

نظرًا لأن الخوارزميات الخاصة بنا أصبحت أكثر فاعلية ، فيمكننا استخدام مجموعة أكبر لمقارنة الوقت ، وترك DFT_slow :
في [9]:

 x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop 

لقد قمنا بتحسين تنفيذنا بأمر ضخم! نحن الآن على بعد حوالي 10 مرات من معيار FFTPACK ، باستخدام بضع عشرات من خطوط Python + NumPy الخالصة. على الرغم من أن هذا لا يزال غير متسق من الناحية الحسابية ، من حيث قابلية القراءة ، فإن إصدار Python أفضل بكثير من شفرة مصدر FFTPACK ، والتي يمكنك مشاهدتها هنا .

فكيف تحقق FFTPACK هذا التسارع الأخير؟ حسنًا ، إنها في الأساس مسألة مسك الدفاتر التفصيلية. يقضي FFTPACK الكثير من الوقت في إعادة استخدام أي حسابات وسيطة يمكن إعادة استخدامها. لا يزال يتضمن إصدارنا خشنة تخصيص الذاكرة الزائدة والنسخ ؛ بلغة منخفضة المستوى مثل Fortran ، من الأسهل التحكم وتقليل استخدام الذاكرة. بالإضافة إلى ذلك ، يمكن توسيع خوارزمية Cooley-Tukey لاستخدام أقسام من حجم آخر غير 2 (ما قمنا بتطبيقه هنا يُعرف باسم Cooley-Tukey Radix FFT على أساس 2). يمكن أيضًا استخدام خوارزميات FFT الأخرى الأكثر تعقيدًا ، بما في ذلك الطرق المختلفة اختلافًا جذريًا استنادًا إلى بيانات الالتفاف (انظر ، على سبيل المثال ، خوارزمية Blueshtein وخوارزمية Raider). يمكن أن يؤدي الجمع بين الامتدادات والأساليب المذكورة أعلاه إلى عمليات تحويل فورييه سريعة للغاية حتى في المصفوفات التي لا يكون حجمها قوة اثنين.

على الرغم من أن الوظائف في بيثون الخالصة قد تكون عديمة الفائدة في الممارسة العملية ، إلا أنني آمل أن توفر بعض المعلومات حول ما يحدث في خلفية تحليل البيانات المستند إلى FFT. كمتخصصين في البيانات ، يمكننا التعامل مع تطبيق "الصندوق الأسود" للأدوات الأساسية التي أنشأها زملاؤنا الأكثر تفكيرًا في الخوارزميات ، ولكني أعتقد بقوة أنه كلما زاد تفهمنا للخوارزميات منخفضة المستوى التي نطبقها على بياناتنا ، الممارسات الأفضل نحن سوف.

تمت كتابة هذا المنشور بالكامل في IPython Notepad. يمكن تنزيل دفتر الملاحظات الكامل هنا أو مشاهدته بشكل ثابت هنا .

قد يلاحظ الكثيرون أن المواد ليست جديدة ، ولكن ، كما يبدو لنا ، تعتبر ذات صلة. بشكل عام ، اكتب ما إذا كانت المقالة مفيدة. في انتظار تعليقاتكم.