التحقق الرسمي هو التحقق من برنامج أو خوارزمية باستخدام برنامج آخر.
هذه واحدة من أقوى الطرق التي تسمح لك بالعثور على جميع نقاط الضعف في البرنامج أو إثبات عدم وجودها.
يمكن الاطلاع على وصف أكثر تفصيلًا للتحقق الرسمي على مثال حل مشكلة
الذئب والماعز والملفوف في مقالتي السابقة.
في هذه المقالة ، سأنتقل من التحقق الرسمي من المهام إلى البرامج ، وسأصفها
كيفية تحويلها إلى أنظمة حكم رسمية تلقائيا.
لهذا ، كتبت نظري عن آلة افتراضية ، على مبادئ رمزية.
تقوم بتوزيع رمز البرنامج وترجمته إلى نظام المعادلات (SMT) ، والذي يمكن بالفعل حله برمجيًا.
نظرًا لأن المعلومات المتعلقة بالحسابات الرمزية تُعرض على الإنترنت بشكل مجزأ إلى حد ما ،
سوف أصف باختصار ما هو عليه.
حسابات الأحرف هي طريقة لتنفيذ برنامج في وقت واحد على مجموعة واسعة من البيانات وهي الأداة الرئيسية للتحقق الرسمي من البرامج.
على سبيل المثال ، يمكننا تعيين شروط الإدخال حيث يمكن للوسيطة الأولى أن تأخذ أي قيم موجبة ، والثانية سالبة ، والثالثة - صفر ، وسيطة المخرجات ، على سبيل المثال ، 42.
سوف تعطينا الحسابات الرمزية في شوط واحد الإجابة ، هل يمكن أن نحصل على النتيجة المرجوة ومثال على مجموعة من معلمات الإدخال هذه. أو دليل على عدم وجود مثل هذه المعلمات.
علاوة على ذلك ، يمكننا تعيين وسيطات الإدخال بشكل عام قدر الإمكان ، وتحديد الإخراج فقط ، على سبيل المثال ، كلمة مرور المسؤول.
في هذه الحالة ، سنجد جميع نقاط الضعف في البرنامج أو سنحصل على دليل على أن كلمة مرور المسؤول آمنة.
قد تلاحظ أن التنفيذ الكلاسيكي لبرنامج يحتوي على بيانات إدخال محددة يمثل حالة خاصة لحالة رمزية.
لذلك ، يمكن أن تعمل شخصيتي VM أيضًا في وضع المحاكاة الخاص بجهاز ظاهري قياسي.
في التعليقات على المقالة السابقة ، يمكنك أن تجد انتقادات عادلة للتحقق الرسمي من خلال مناقشة نقاط الضعف فيها.
المشاكل الرئيسية هي كما يلي:
- انفجار اندماجي ، لأن التحقق الرسمي يقع في النهاية على P = NP
- من الصعب التحقق من معالجة المكالمات إلى نظام الملفات والشبكات ووحدات التخزين الخارجية الأخرى
- الخلل في المواصفات ، عندما تصور العميل أو المبرمج شيئًا واحدًا ، لكنه لم يصفه بدقة في بيان العمل.
نتيجة لذلك ، سيتم التحقق من البرنامج والوفاء بالمواصفات ، لكنه لن يفعل على الإطلاق ما توقعه المبدعون منه.
نظرًا لأنني في هذه المقالة أعتبر بشكل أساسي تطبيق التحقق الرسمي عمليًا ، فلن أتغلب على جبهتي على الجدار بعد ، وسأختار نظامًا يكون فيه التعقيد الحسابي وعدد المكالمات الخارجية ضئيلًا.
نظرًا لأن العقود الذكية تتناسب مع هذه المتطلبات بأفضل طريقة ، فقد وقع الاختيار على عقود RIDE من منصة Waves: فهي ليست كاملة من تورينج ، والحد الأقصى لتعقيدها محدود بشكل مصطنع.
لكننا سننظر فيها فقط من الجانب التقني.
بالإضافة إلى الكل ، بالنسبة إلى أي عقود ، سيكون التحقق الرسمي مطلوبًا بشكل خاص: من المستحيل عادة تصحيح خطأ العقد بعد إطلاقه.
وقد يكون سعر هذه الأخطاء مرتفعًا للغاية ، حيث يتم تخزين مبالغ كبيرة من الأموال في العقود الذكية.
تتم كتابة الجهاز الظاهري لشخصيتي في PHP و Python ، ويستخدم Microsoft Research's Z3Prover لحل صيغ SMT الناتجة.
في جوهرها يكمن بحث قوي متعدد المعاملات ، والتي
يتيح لك العثور على حلول أو نقاط ضعف ، حتى لو كان يتطلب الكثير من المعاملات.
حتى
Mythril ، أحد أقوى الأطر الرمزية للبحث في نقاط الضعف Ethereum ، أضافت هذه الميزة قبل بضعة أشهر فقط.
ولكن تجدر الإشارة إلى أن عقود الأثير أكثر تعقيدًا وتمتلك Turing.
يقوم PHP بترجمة الكود المصدري للعقد RIDE الذكي إلى برنامج نصي بيثون يقدم فيه البرنامج في شكل نظام لشروط وشروط العقد الخاصة بعمليات الانتقال الخاصة بهم المتوافقة مع Z3 SMT:
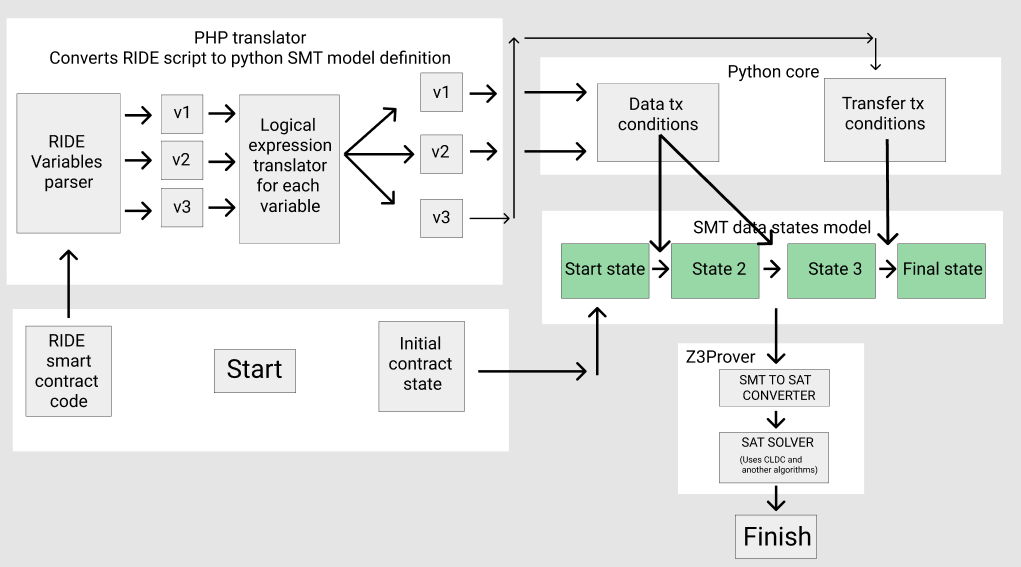
الآن سوف أصف ما يحدث في الداخل بمزيد من التفصيل.
ولكن أولا ، بضع كلمات حول لغة العقود الذكية RIDE.
إنها لغة برمجة وظيفية وقائمة على التعبير وهي كسولة على النحو المنشود.
يتم تنفيذ RIDE بمعزل داخل blockchain ، ويمكنه استخراج المعلومات وكتابتها من وحدة التخزين المرتبطة بمحفظة المستخدم.
يمكنك إرفاق عقد RIDE بكل محفظة ، وستكون نتيجة التنفيذ TRUE أو FALSE فقط.
TRUE تعني أن العقد الذكي يسمح بالمعاملة ، و FALSE يمنعها.
مثال بسيط: قد يمنع البرنامج النصي التحويل إذا كان رصيد المحفظة أقل من 100.
على سبيل المثال ، سوف آخذ كل نفس الذئب والماعز والملفوف ، لكن تم تقديمه بالفعل في شكل عقد ذكي.
لن يتمكن المستخدم من سحب الأموال من المحفظة التي تم نشر العقد عليها حتى يحيل الجميع إلى الجانب الآخر.
# let contract = tx.sender let human= extract(getInteger(contract,"human")) let wolf= extract(getInteger(contract,"wolf")) let goat= extract(getInteger(contract,"goat")) let cabbage= extract(getInteger(contract,"cabbage")) # -, 4 . # . match tx { case t:DataTransaction => # let newHuman= extract(getInteger(t.data,"human")) let newWolf= extract(getInteger(t.data,"wolf")) let newGoat= extract(getInteger(t.data,"goat")) let newCabbage= extract(getInteger(t.data,"cabbage")) #0 , , 1 let humanSide= human == 0 || human == 1 let wolfSide= wolf == 0 || wolf == 1 let goatSide= goat == 0 || goat == 1 let cabbageSide= cabbage == 0 || cabbage == 1 let side= humanSide && wolfSide && goatSide && cabbageSide # , . let safeAlone= newGoat != newWolf && newGoat != newCabbage let safe= safeAlone || newGoat == newHuman let humanTravel= human != newHuman # , - . let t1= humanTravel && newWolf == wolf + 1 && newGoat == goat && newCabbage == cabbage let t2= humanTravel && newWolf == wolf && newGoat == goat + 1 && newCabbage == cabbage let t3= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage + 1 let t4= humanTravel && newWolf == wolf - 1 && newGoat == goat && newCabbage == cabbage let t5= humanTravel && newWolf == wolf && newGoat == goat - 1 && newCabbage == cabbage let t6= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage - 1 let t7= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage let objectTravel = t1 || t2 || t3 || t4 || t5 || t6 || t7 # . # 1 0, # , # - side && safe && humanTravel && objectTravel case s:TransferTransaction => # human == 1 && wolf == 1 && goat == 1 && cabbage == 1 # case _ => false }
PHP أولاً وقبل كل شيء يستخلص من العقد الذكي جميع المتغيرات في شكل مفاتيحهم والمتغير المقابل للتعبير المنطقي.
cabbage: extract ( getInteger ( contract , "cabbage" ) ) goat: extract ( getInteger ( contract , "goat" ) ) human: extract ( getInteger ( contract , "human" ) ) wolf: extract ( getInteger ( contract , "wolf" ) ) fState: human== 1 && wolf== 1 && goat== 1 && cabbage== 1 fState: wolf: goat: cabbage: cabbageSide: cabbage== 0 || cabbage== 1 human: extract ( getInteger ( contract , "human" ) ) newGoat: extract ( getInteger ( t.data , "goat" ) ) newHuman: extract ( getInteger ( t.data , "human" ) ) goatSide: goat== 0 || goat== 1 humanSide: human== 0 || human== 1 t7: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage t3: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage + 1 t6: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage - 1 t2: humanTravel && newWolf== wolf && newGoat== goat + 1 && newCabbage== cabbage t5: humanTravel && newWolf== wolf && newGoat== goat - 1 && newCabbage== cabbage t1: humanTravel && newWolf== wolf + 1 && newGoat== goat && newCabbage== cabbage t4: humanTravel && newWolf== wolf - 1 && newGoat== goat && newCabbage== cabbage safeAlone: newGoat != newWolf && newGoat != newCabbage wolfSide: wolf== 0 || wolf== 1 humanTravel: human != newHuman side: humanSide && wolfSide && goatSide && cabbageSide safe: safeAlone || newGoat== newHuman objectTravel: t1 || t2 || t3 || t4 || t5 || t6 || t7
يقوم PHP بعد ذلك بتحويلها إلى وصف نظام Python متوافق مع Z3Prover SMT.
يتم التفاف البيانات في دورة حيث تحصل متغيرات التخزين على مؤشر i ، ومؤشر متغيرات المعاملة i + 1 ، وتعيين المتغيرات مع التعبيرات قواعد الانتقال من الحالة السابقة إلى التالية.
هذا هو جوهر الجهاز الظاهري لدينا ، والذي يوفر محرك بحث متعدد المعاملات.
fState: And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final: fState[Steps] fState: wolf: goat: cabbage: cabbageSide: Or( cabbage[i] == 0 , cabbage[i] == 1 ) goatSide: Or( goat[i] == 0 , goat[i] == 1 ) humanSide: Or( human[i] == 0 , human[i] == 1 ) t7: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t3: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] + 1 ) t6: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] - 1 ) t2: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage == cabbage[i] ) t5: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage == cabbage[i] ) t1: And( And( And( humanTravel[i] , wolf == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t4: And( And( And( humanTravel[i] , wolf == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) safeAlone: And( goat[i+1] != wolf , goat[i+1] != cabbage ) wolfSide: Or( wolf[i] == 0 , wolf[i] == 1 ) humanTravel: human[i] != human[i+1] side: And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) safe: Or( safeAlone[i] , goat[i+1] == human[i+1] ) objectTravel: Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) data: And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] )
يتم فرز الشروط وإدراجها في قالب البرنامج النصي المصمم لوصف نظام SMT في بيثون.
قالب فارغ import json from z3 import * s = Solver() Steps=7 Num= Steps+1 $code$
بالنسبة إلى الحالة الأخيرة من السلسلة بأكملها ، يتم تطبيق القواعد المحددة في قسم معاملة النقل.
لذلك ، سوف تبحث Z3Prover عن مجموعة من الشروط التي تسمح لك في نهاية المطاف بسحب الأموال من العقد.
نتيجة لذلك ، نحصل تلقائيًا على نموذج SMT يعمل بشكل كامل في عقدنا.
يمكنك أن ترى أنه مشابه جدًا للنموذج من مقالتي السابقة ، والذي كتبته يدويًا.
قالب مكتمل import json from z3 import * s = Solver() Steps=7 Num= Steps+1 human = [ Int('human_%i' % (i + 1)) for i in range(Num) ] wolf = [ Int('wolf_%i' % (i + 1)) for i in range(Num) ] goat = [ Int('goat_%i' % (i + 1)) for i in range(Num) ] cabbage = [ Int('cabbage_%i' % (i + 1)) for i in range(Num) ] nothing= [ And( human[i] == human[i+1], wolf[i] == wolf[i+1], goat[i] == goat[i+1], cabbage[i] == cabbage[i+1] ) for i in range(Num-1) ] start= [ human[0] == 1, wolf[0] == 0, goat[0] == 1, cabbage[0] == 0 ] safeAlone= [ And( goat[i+1] != wolf[i+1] , goat[i+1] != cabbage[i+1] ) for i in range(Num-1) ] safe= [ Or( safeAlone[i] , goat[i+1] == human[i+1] ) for i in range(Num-1) ] humanTravel= [ human[i] != human[i+1] for i in range(Num-1) ] cabbageSide= [ Or( cabbage[i] == 0 , cabbage[i] == 1 ) for i in range(Num-1) ] goatSide= [ Or( goat[i] == 0 , goat[i] == 1 ) for i in range(Num-1) ] humanSide= [ Or( human[i] == 0 , human[i] == 1 ) for i in range(Num-1) ] t7= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t3= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] + 1 ) for i in range(Num-1) ] t6= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] - 1 ) for i in range(Num-1) ] t2= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t5= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t1= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t4= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] wolfSide= [ Or( wolf[i] == 0 , wolf[i] == 1 ) for i in range(Num-1) ] side= [ And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) for i in range(Num-1) ] objectTravel= [ Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) for i in range(Num-1) ] data= [ Or( And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] ) , nothing[i]) for i in range(Num-1) ] fState= And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final= fState
بعد الإطلاق ، يحل Z3Prover عقدًا ذكيًا ويعرض سلسلة معاملات لنا ، مما سيتيح لنا سحب الأموال:
Winning transaction chain found: Data transaction: human= 0, wolf= 0, goat= 1, cabbage= 0 Data transaction: human= 1, wolf= 0, goat= 1, cabbage= 1 Data transaction: human= 0, wolf= 0, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 0, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Transfer transaction
بالإضافة إلى عقد إعادة التوجيه ، يمكنك تجربة عقودك الخاصة أو تجربة هذا المثال البسيط ، والذي يتم حله في معاملتين.
let contract = tx.sender let a= extract(getInteger(contract,"a")) let b= extract(getInteger(contract,"b")) let c= extract(getInteger(contract,"c")) let d= extract(getInteger(contract,"d")) match tx { case t:DataTransaction => let na= extract(getInteger(t.data,"a")) let nb= extract(getInteger(t.data,"b")) let nc= extract(getInteger(t.data,"c")) let nd= extract(getInteger(t.data,"d")) nd == 0 || a == 100 - 5 case s:TransferTransaction => ( a + b - c ) * d == 12 case _ => true }
نظرًا لأن هذا هو الإصدار الأول ، فإن بناء الجملة محدود للغاية ويمكن أن تحدث الأخطاء.
في المقالات التالية ، أخطط لتسليط الضوء على التطوير الإضافي لـ VM ، وإظهار كيف يمكن إنشاء عقود ذكية تم التحقق منها رسميًا من خلال مساعدتها ، وليس فقط حلها.
يتوفر جهاز افتراضي رمزي على الموقع
http://2.59.42.98/hyperbox/المصادر متاحة على جيثب:
http://github.com/scp1001/hyperboxكل منطق VM موجود في ملفين ، hyperbox.php و hyperbox2.php