تعيين ثنائي الرياضيات منطقة لا نهاية لها من الحد الأدنى من الأسطح

أظهر اثنان من علماء الرياضيات على أساس نظرية رياضية غير معروفة منذ 30 عامًا أن الحد الأدنى من الأسطح التي تشبه فيلم الصابون يظهر بأعداد كبيرة على مجموعة واسعة من الأشكال

في نهاية عام 2011 ، سمع برايان وايت أحيانًا طرقًا على باب مكتبه في ستانفورد. في الخارج ، في هذه اللحظات ، ينتظره عالمان رياضيان شابان ، فرناندو كودا ماركيز وأندريه نيفيس ، اللذان كان لديهما دائمًا نفس السؤال: هل أمام وايت بضع دقائق لمساعدتهما على اكتشاف إحدى الأجزاء الغامضة من أطروحة غير معروفة لعدة مئات صفحات مكتوبة قبل ثلاثين سنة؟

قدمت الرسالة ، التي كتبها جون بيتس ، آلية قوية لبناء الحد الأدنى من الأسطح - هياكل مماثلة لفيلم الصابون والفقاعات - ضمن مجموعة واسعة من الأشكال. عندما يمكن بناء حد أدنى للسطح على شكل ما ، فإن هذا الأخير يجعل من الممكن دراسة هندسة المساحة المحيطة به. تظهر مثل هذه الأسطح في العديد من المشكلات العلمية ، بدءًا من دراسة الثقوب السوداء وحتى تطوير الجزيئات الحيوية.

ومع ذلك ، فقد ظلت أطروحة بيتس طوال هذه السنوات خارج نطاق اهتمام العلماء - ربما لأنه كان من الصعب قراءتها بشكل لا يصدق. اقتنع ماركيز ونيفيس بوجود إمكانات كبيرة فيه. وقال نيفيس ، وهو الآن أستاذ بجامعة شيكاغو: "لقد كان واضحًا بالنسبة لنا أن هذه النظرية قد تم التقليل من أهميتها تمامًا ولم يتم ملاحظتها."

على الرغم من أن وايت لم يسأل الزوجين أبدًا عن سبب اهتمامهما بعمل بيتس ، إلا أنهما قالا في كل مرة إن اهتمامهم "أكاديمي بحت" ، كما قال نيفيس. ومع ذلك ، كان لديهم هدف محدد - إثبات فرضية ويلمور قبل 50 عامًا ، والتي تتناول مسألة العثور على أفضل شكل ممكن من الدونات (التفاصيل لاحقًا). بعد ثلاثة أشهر من الصراع مع أفكار أطروحة بيتس ، حقق ماركيز ونيفيس هدفهما ، وحازا على العديد من الجوائز والمراجعات الإيجابية.

لكن في السنوات القليلة الماضية ، استطاعوا دفع أفكار بيتس إلى أبعد من ذلك. وجد بيتس ، مع أمينه الفني ، فريدريك ألجرين ، طريقة للتأكد من أن كل شخصية في عدد صغير من الأبعاد لها سطح واحد على الأقل. الآن ، أظهر ماركيز ونيفيس ، باستخدام مجموعة من علماء الرياضيات الشباب الذين تجمعوا حولهم ، استنادًا إلى أفكار المجرين وبيتس ، أنه في الحالة العامة يجب أن تحتوي هذه الأشكال على العديد من الأسطح الدنيا - بلا حدود العديد من الأسطح المزدحمة والاكتظاظ في جميع أنحاء الشخصيات. كتبت كارين أولينبيك من جامعة تكساس في رسالة بريد إلكتروني: "هذا إنجاز كبير".

قال ريتشارد شوين من جامعة كاليفورنيا في إيرفين ، الذي نصح نيفيس قبل حوالي 15 عامًا: "يتطلب الأمر بذل جهد كبير لإنشاء سطح واحد بسيط". "حقيقة أن هناك الكثير منهم مدهش".

أدت هذه النهضة في نظرية المغرين وبيتس إلى انفجار النشاط في العامين الماضيين. وقال وايت: "النتائج سريعة للغاية وبأعداد كبيرة يصعب معها تتبعها". "يبدو مثيرا للاهتمام ورائع بالنسبة لي."

بمناسبة سلسلة الجبال

اغمس السلك المنحني في محلول صابون ، أو قم بتفجير فقاعة صابون ، وسيشكل السائل بسرعة سطح أصغر منطقة ممكنة. احتلت هندسة هذه الأسطح الدنيا علماء الرياضيات لمئات السنين. تظهر في مجالات مختلفة ، من الهندسة المعمارية ، حيث يلهم الحد الأدنى من السطح تصميم الأسطح وغيرها من الهياكل ، إلى إنشاء جزيئات دقيقة لتوصيل الأدوية. منذ خمس سنوات ، عندما ابتكر فريق من العلماء جزيئات مسامية قادرة على حمل العقاقير أو الهرمونات داخلها ، وجدوا أن بعض الجزيئات قد اتخذت شكل gyroid ، سطح متكرر إلى ما لا نهاية ، وتشبه بعض أجزاء منه فيلمًا صابونًا.

من الناحية الفنية ، يعتبر علماء الرياضيات أن أفلام الصابون الموجودة على السلك فقط هي بمثابة أسطح ذات حد أدنى من السطح ، ولكن ليس وفقاعات الصابون ، لأنه في مساحة مجردة لا توجد فيها جزيئات هواء ، فإن الفقاعة سوف تنحرف إلى حد ما. ومع ذلك ، فإن الفيلم على السلك لا يرضي تماما علماء الرياضيات. الجزء الداخلي هو سطح أملس ، ولكن سلكه ينفصل بشكل حاد. من المنطقي التفكير فيما إذا كان من الممكن تمديد هذا السطح خارج حدود حدود الأسلاك بحيث يستمر في الظهور كفيلم صابون في كل منطقة على حدة. هذا ممكن في بعض الأحيان ، ويمتد السطح إلى ما لا نهاية. في بعض الأحيان يعود السطح ويتقاطع بشكل محرج مع نفسه ، أو يواجه صعوبات أخرى.


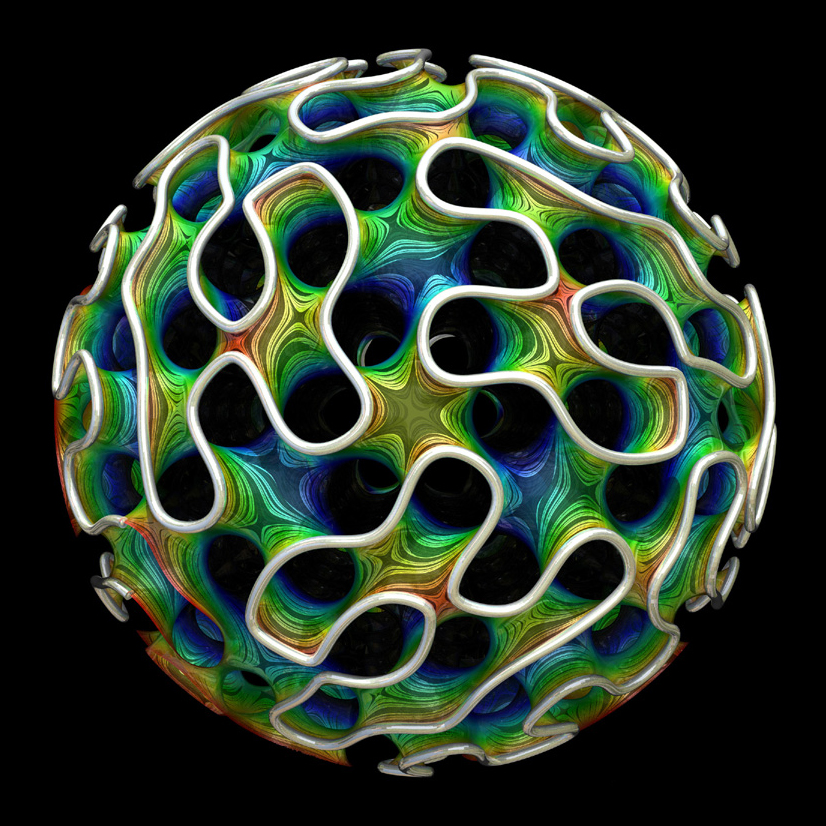Gyroid - نوع من الحد الأدنى للسطح الذي حدث أثناء تصميم الجسيمات الدقيقة لتسليم الدواء

في الفضاء العادي ، وهذا يستنفد كل الاحتمالات. لكن علماء الرياضيات والعلماء الآخرين غالباً ما ينظرون إلى عوالم أخرى تختلف عن الفضاء الثلاثي الأبعاد الذي لا نهاية له والذي اعتدنا عليه - منحني أو محدود ، مثل التشبيهات ثلاثية الأبعاد للكرة أو سطح التوروز. تتمتع هذه الأشكال بإمكانيات جديدة مثيرة للاهتمام: الحد الأدنى من الأسطح التي تنحني وتغلق في صورة نهائية مغلقة لا تتطلب دعمًا سلكيًا.

في نظرية النسبية ، تلعب هذه الأسطح الدنيا المحدودة دور أفق الحدث للثقوب السوداء. وإذا كان يمكن العثور عليها على أي شخصية ، فإن هذا يساعد علماء الرياضيات على التفكير في هندستهم من جوانب مختلفة: فهم يعطون قالبًا لقطع الشكل (أو المنوع ) إلى قطع أبسط محتملة ، يشيرون إلى مناطق الانحناء الإيجابي داخل المنوع - إلى أقسام ، التقويس للداخل ، مثل كرة أو ثقب أسود ، بدلاً من التقويس للخارج.

"نحن نعرف القليل عن الفتحات ذات الانحناء الإيجابي" ، قال شوين.

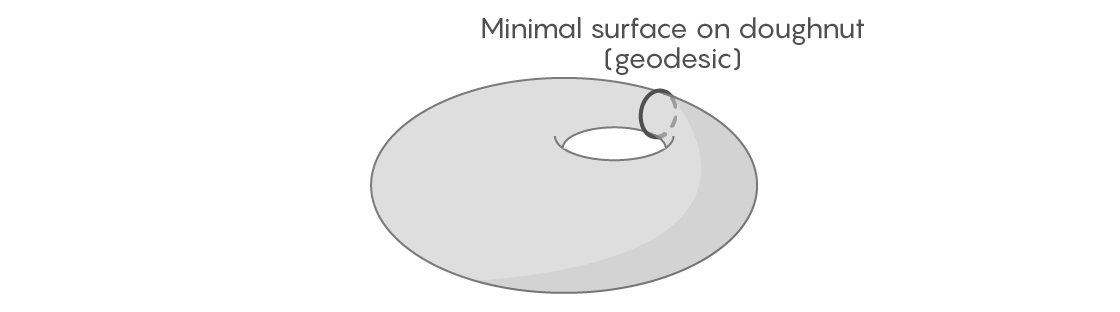
ومع ذلك ، غالبا ما يكون من الصعب إثبات وجود حد أدنى للسطح داخل الشكل. لفهم سبب ذلك ، فكر في إصدار ثنائي الأبعاد لهذه المشكلة. مسألة إيجاد الحد الأدنى للسطح أمر منطقي في أي بعد: يعتبر علماء الرياضيات أن السطح مجرد شكل ذو بعد أقل من الفضاء الذي يعيش فيه. لذلك في عالم ثنائي الأبعاد ، فإن المنحنيات "الجيوديسية" المكونة من أقصر الطرق التي تربط النقاط القريبة ستكون الحد الأدنى للسطح.

بالنسبة لبعض الأشكال ثنائية الأبعاد ، يمكنك العثور بسهولة على منحنيات جيوديسية مغلقة في حلقة محدودة. خذ سطح التورز - حتى ليس بالضرورة ومتساوٍ ؛ دعه يشتمل على مخالفات وانتفاخات. إذا قمنا بلف مثل هذا الدونيت بشريط مرن يمر في وسطه ، يمكننا أن نتخيل كيف نقوم بتشديده وتحويله إلى مواقع مختلفة محتملة. واحد منهم سيكون الأقصر - سيكون منحنى جيوديسيا بحكم التعريف.



ولكن إذا كان المجال هو رقمنا ، فلن ينجح هذا النهج. في كرة مسطحة تمامًا ، من السهل العثور على منحنى جيوديسي - سيكون خط الاستواء والدوائر الكاملة الأخرى. لكن على سطح غير مستوٍ ، على سبيل المثال ، على سطح الأرض ، ليس من الواضح أين تذهب المنحنيات الجيوديسية وما إذا كان أي منها مغلقًا في حلقة. يمكنك أن تتخيل كيف نلف الأرض بشريط مرن ، كما في حالة الكعك. لكن إذا بدأت في تحريكه ، ومحاولة تقصيره ، فسوف يتقلص إلى نقطة واحدة ، لأنه على عكس الكعك ، فإن الكرة لا تحتوي على ثقب للتمسك بالمرونة.

ومع ذلك ، فإن هذا الفشل الذريع مع شريط مرن محفوف بجراثيم النجاح. إذا تم اعتراض خط الاستواء من الكرة المستديرة بواسطة شريط مرن ، فإن الطريقة الوحيدة لتحويله - لإضافة موجات إليه - ستجعله أطول. إذا قمت بنقلها بطريقة مختلفة ، لأعلى أو لأسفل إلى خط عرض جديد ، فستصبح أقصر. لذلك ، سيكون خط الاستواء هو أقصر منحنى من وجهة نظر واحدة ، والأطول من جهة أخرى.

وهذا يجعل خط الاستواء يتعلق بسرج الممر الجبلي ، وأعلى نقطة على جانب واحد (من المسار عبر الجبال) والأدنى على الجانب الآخر (من المسار إلى القمم القريبة). وهذا ليس مجرد تشبيه ضعيف: كقاعدة عامة ، يتبين أن الحد الأدنى من الأسطح هو مثل هذه السروج ، لكن سلاسل جبالها تعيش في عالم يصعب تصوره.



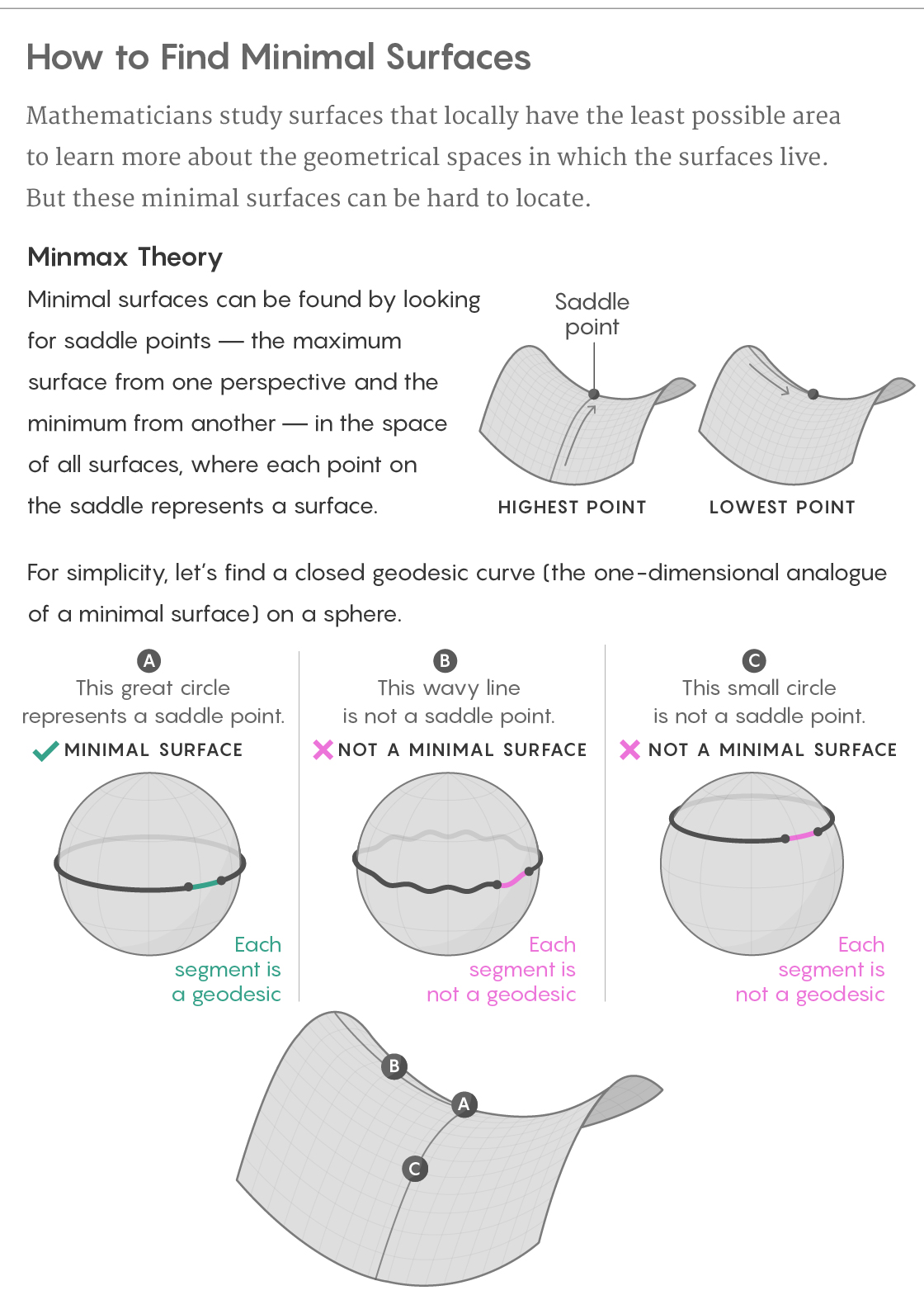
عند تحديد الحد الأدنى لسطح الشكل ، يمكننا النظر في عالم جديد يتكون من جميع الأسطح المحدودة الممكنة الموجودة داخل هذا الشكل - وسنسميها "سطح الأسطح". كل نقطة من مساحة السطح يتوافق مع السطح بأكمله بالكامل على الشكل الأصلي. بعد ذلك يمكننا أن نعتبر مساحة كل سطح هي ارتفاع النقطة المقابلة في مساحة الأسطح ، ونتيجة لذلك سيكون لدى عالمنا تضاريس طبيعية. البحث عن الحد الأدنى من الأسطح على الشكل الأصلي يصبح البحث عن السروج في مساحة السطح.

في عام 1917 ، استخدم جورج ديفيد بيرخوف هذا النهج لإظهار أن أي كرة ، وعرة أو ناعمة ، يجب أن يكون لها منحنى جيوديسي مغلق. بعد حوالي ستة عقود ، وسّع المغرن وبيتس ببراعة أفكار بيرخوف من خلال وضع علامة على التضاريس السطحية للأسطح على جميع الأشكال المحددة بأبعاد من ثلاثة إلى سبعة ، ثم استخدموا هذه التضاريس لإثبات أن هذه الأشكال لها دائمًا سطح واحد مغلق على الأقل. وقال نيفيس إن أطروحة بيتس من عام 1981 حول نظرية Minmax - التي سميت لأن السرج هو الحد الأدنى والحد الأقصى على حد سواء - كانت "مذهلة للغاية".

ومع ذلك ، كان معقد للغاية. وقال شوين إن قلة من الناس فهموا الفروق الدقيقة في النظرية ، وادعى بعض علماء الرياضيات الذين درسوها أنها غير مؤكدة تمامًا. وقال "لا أعتقد أنه كان هناك أي شك في أنها كانت مهمة للغاية ومهمة". "لكن كان من غير الواضح مدى امتلاءها".

العمل على نظرية Minmax جاء تدريجيا إلى شيء. وقال نيفيس "لقد تم نسيان عمل بيتس من قبل المجتمع الرياضي منذ حوالي 30 عامًا". لم يتم إحيائها حتى التقى نيفيس وماركيز في عام 2006 في مصعد المبنى الرياضي بجامعة برينستون.

فوق الممر الجبلي

في تلك اللحظة ، وصل ماركيز إلى برينستون لإلقاء محاضرة ؛ حصلت نيفيس على وظيفة هناك بعد فترة وجيزة من الدفاع عن الدكتوراه. كلاهما كان البرتغالية لغتهم الأم (كان ماركيز من البرازيل ونيفيس من البرتغال) ، ووجدوا بسهولة لغة مشتركة. يتذكر ماركيز ، وهو الآن أستاذ في جامعة برينستون: "ثم تحدثت معه للمرة الأولى ، لكنه تحدث معي كما لو كنا أصدقاء لمدة 10 سنوات".

ثم وجدوا أن مناقشة الأفكار الرياضية كانت طبيعية بالنسبة لهم. لديهم أنماط مختلفة: ماركيز أكثر هدوءًا ، ونيفيس أكثر كثافة. ولكن هذا بمثابة علامة زائد بالنسبة لهم. قال ماركيز: "من النادر جدًا العثور على شخص يكملك جيدًا".

كان كلاهما حريصًا على إيجاد بعض المشكلات الرياضية المعقدة التي يمكن أن تندمج فيها. لعدة سنوات ، ألقى الزوجان أفكارًا في كل مرة عبرت فيها طرقهما "لمعرفة ما تأخر" ، كما قال نيفيس. "كان لدينا مليون فكرة ، ونتيجة لذلك ، تمت تصفية إحدى هذه الأفكار وتحولت إلى شيء تم تشكيله."

تبين أن المشكلة التي تمت تصفيتها هي المشكلة الشهيرة في "فرضية ويلمور". إنها تقترح إيجاد شكل torus يقلل من الحجم المعروف باسم طاقة Willmore ، والتي تقيس الفرق بين شكل معين والمجال الدائري. في عام 1965 ، اقترح ويلمور أنه سيكون أكثر الكعك دائرية الشكل المتناظر بشكل خاص ، والمعروف باسم توريس كليفورد ، ومع ذلك ، على الرغم من المحاولات الكثيرة ، لا يمكن إثبات الفرضية لأي شخص.


ماركيز (يسار) ونيفيس

طور ماركيز ونيفيس مقاربة واعدة ، ولكن لكي تنجح ، احتاجا إلى العنصر الأخير: نظرية الحد الأدنى. لقد ظنوا أن إتقان هذه النظرية وكتابة العمل النهائي سيستغرق من أسبوعين إلى ثلاثة أسابيع - حتى يفتحوا كتاب بيتس. "لقد صدمنا - ما كل شيء؟ - قال نيفيس. "كان الكتاب جافًا بشكل لا يصدق".

نمت النظريات المنفصلة إلى عدة صفحات - وكان هذا مجرد وصف للنظريات ، وليس دليلًا عليها. كانت النظرية الرئيسية ببساطة من الصعب العثور عليها. "أتذكر كيف جاء فرناندو إلى مكتبي وقال: لقد وجدت بيان النظرية!" - قال نيفيس.


ثور كليفورد

عندما تعثروا ، صنعوا لعبة البوكر وطلبوا المساعدة من وايت ، أحد الأشخاص القلائل الذين فهموا معظم أعمال بيتس (على الرغم من أن وايت نفسه وصف هذه المحادثات بأنها "عمياء وأعمى رائد" ؛ وتخرج بيتس نفسه ، أستاذ بجامعة إيه آند إم في تكساس ، الكتابة تعمل على نظرية minmax قبل بضعة عقود). يتذكر نيفيس قائلاً: "لقد كان لدينا دوافع لا تصدق ، وبالتالي تمكنا من الاختراق". "لكن ذلك لم يكن مهمة لضعاف القلب".

بحلول الوقت الذي أنهى فيه ماركيز ونيفيس برهانهما على فرضية ويلمور ، فهما نظرية مينماكس أفضل من أي عالم رياضيات آخر. كانوا مقتنعين بأن إمكاناتها تمتد إلى أبعد من مجرد بيان الفرضية. قال نيفيس: "كنا نعرف أن لدينا نظرية قوية للغاية". - في كل مرة ، باستخدام الطريقة لإثبات نتيجة معينة ظلت مفتوحة لفترة طويلة ، أنت تفهم أن هناك شيء ما فيها. هذا يشير إلى أن الأمر يستحق المتابعة أكثر. "

لا ينتج رسم minmax من Almgren و Pitts سرج واحد فقط ، ولكن عدد لا حصر له منهم. من الناحية النظرية ، يجب أن يتوافق هذا مع عدد لا حصر له من الأسطح الدنيا للشكل الأصلي. لكن المغرين وبيتس لم يتمكنوا من إظهار أن الحد الأدنى للأسطح التي تم الحصول عليها بهذه الطريقة كان مختلفًا. وبالتالي ، فإن الشيء الوحيد الذي يمكن قوله بالتأكيد هو أن كل شخصية بها سطح واحد على الأقل.

بعد ذلك ، "تطور الموضوع قد توقف عمليا" ، قال نيفيس. "لقد كانت أفضل نتيجة لأكثر من 30 عامًا."

هناك حاجة إلى عنصر جديد ، ووجده ماركيز ونيفيس. القائمة التي لا نهاية لها من أسطح minmax ، كما أظهرت في عام 2016 ، تتصرف مثل ترددات الأسطوانة.

أظهر عالم الرياضيات الألماني ويل في عام 1911 أن الترددات الأساسية للطبل لها خاصية واحدة غير متوقعة: بشكل عام ، تعتمد الترددات العالية فقط على حجم الأسطوانة ، وليس على شكلها. أظهر ماركيز ونيفيس ، مع يوجين ليكوموفيتش من معهد ماساتشوستس للتكنولوجيا ، أن أسطح Minmax تلبي قانونًا رياضيًا مشابهًا لقانون ترددات الطبل. على وجه الخصوص ، يتم تحديد المساحات السطحية تقريبًا من خلال مقدار المساحة التي يعيشون فيها ، وليس حسب شكلها.

هذه النتيجة ، التي وضعت حداً للفرضية التي تم طرحها قبل عدة عقود ، سمحت لماركيز ونيفيس بالعرض في عام 2017 - هذه المرة ساعدهما كاي إير من جامعة طوكيو - حيث تحتوي قائمة minmax على معظم الأرقام على عدد لا حصر له من الأسطح الدنيا المختلفة. علاوة على ذلك ، أظهروا أن هذه الأسطح "كثيفة": تظهر بجانب كل نقطة في الفضاء المحيط. الحدس الداعم لهذا الاستنتاج هو أنه من أجل أن يحدد حجم المساحة مناطق موقع الحد الأدنى من الأسطح ، يجب على الأخير "بطريقة ما" أن يرى الحجم بأكمله. وقال ماركيز: "هذا يقول إن هؤلاء الرجال في تنوعهم".

بعد ذلك بشهرين ، أظهر هذا الزوجان ، مع أنطوان صن ، طالب الدراسات العليا في ماركيز ، أنه إذا ذهبت إلى قائمة أسطح minmax ، فسترى أنها تملأ المساحة بالتساوي - ما يسميه علماء الرياضيات "equidistribution".

قال وايت: "عندما سمعت أنها كانت موزعة بالتساوي ، لقد دهشت". "يبدو أن الناس ما كان يجب أن يكونوا قادرين على إثبات هذه النتيجة خلال حياتي".

في العامين الماضيين ، انضم العديد من علماء الرياضيات إلى السؤال. على سبيل المثال ، في يناير / كانون الثاني ، أثبت Xin Zhou من جامعة كاليفورنيا في سانتا باربرا ، استنادًا إلى أعمال سابقة قام بها ماركيز ونيفيس ، أن معظم الأسطح الدنيا في قائمة Almgren و Pitts تختلف بالنسبة لبعض الشخصيات ، مما يضع نقطة لطيفة في هذه المسألة. وقال وايت: "هذا يغلق هذا الموضوع جيدًا ، وهو مفتوح منذ أيام المغرين وبيتس في الثمانينات".

تأخذ مجموعة النتائج هذه في الاعتبار تقريبًا كل رقم في الأبعاد من ثلاثة إلى سبعة - باستثناء أنعم الأشكال ، بغض النظر عن كونها غير بديهية. لكن في شهر يونيو الماضي ، تمكنت Sunn من إثبات أن كل رقم في هذه الأبعاد ، بما في ذلك الأبعاد الأكثر تقريبًا ، لديه بلا حدود العديد من الأسطح المغلقة ، مما يؤكد فرضية أخرى عمرها عدة عقود.

لا يزال من غير الواضح ما إذا كانت الكثافة والتكافؤ سوف يتصرفان بشكل موحد ، وكذلك كيف لا تعمل نظرية minmax في المشعبات المدمجة ، أو في ثمانية أبعاد أو أكثر (ومع ذلك ، حقق العمل الجديد بعض النجاح هنا أيضًا). يتوقع علماء الرياضيات أننا سنكون قادرين على الإجابة على العديد من الأسئلة في وقت أقرب مما يبدو.

"كل شيء يتطور بسرعة كبيرة" ، قال نيفيس. "كل أسبوع ألق نظرة على الموقع باستخدام مخططات arxiv ، وأرى هناك كيف قرر شخص ما شيء آخر."

من وجهة نظر واحدة ، تمثل هذه الأعمال نهاية - أو نهاية - قصة معلقة في حالتها غير المكتملة منذ ما يقرب من أربعة عقود. ولكن هذه أيضًا بداية جديدة: بدأ علماء الرياضيات للتو في فهم أن هذه الأفكار الجديدة المتعلقة بالحد الأدنى من الأسطح يمكن أن تخبرنا عن المساحات التي يعيشون فيها.

وقال شوين: "يمكنني أن أفترض أن هناك طرقًا أخرى مثيرة للاهتمام لتطبيق هذه المعرفة ستظهر قريبًا ، لكن ما الذي لا يمكنني قوله بالتأكيد". "أنا متأكد من أن هذا سيكون أحد الاتجاهات الرئيسية في الهندسة."