كيف يمكن للحوسبة الكمية أن تؤثر على تطوير البرمجيات

مرحبا بالجميع!

منذ ما يقرب من ستة أشهر ، كانت دار النشر تعمل بنشاط على موضوع الحوسبة الكمية وإمكانية تطبيقها العملية. لفترة طويلة ، لم يكن من الممكن العثور على مقالة جديرة بالترجمة حول هذا الموضوع المشوق ، إلى أن ظهر هذا المقال على مدونة Oracle. سيكون المنشور بمثابة مقدمة ممتازة للبرامج والأجهزة ومشاكل العلوم الطبيعية البحتة لهذا النموذج الجديد ، لذلك القراءة أمر لا بد منه.



على مدى الأشهر والسنوات الماضية ، نما الاهتمام في الحوسبة الكمومية بشكل ملحوظ. تظهر مواد جديدة باستمرار من معاهد البحوث أو الشركات أو المؤسسات الحكومية ، تخبرنا عن الإنجازات الكبيرة في هذا المجال. في الوقت نفسه ، تناقش المقالات ذات الأساس الفني الأضعف العواقب المحتملة للحوسبة الكمومية ، وتتراوح التوقعات بين اختراق أحدث تقنيات التشفير ووعد علاج جميع الأمراض وإكمال العمل على إنشاء الذكاء الاصطناعي الكامل. ومع ذلك ، ليست كل هذه التوقعات واقعية بنفس القدر.

إذا كنت مبرمجًا متيقظًا ، فقد تتساءل عن الخط الفاصل بين الحقائق والخيال في هذه الحسابات ، وكيف ستؤثر الحوسبة الكمية على تطوير البرمجيات في المستقبل.

بطبيعة الحال ، تبقى سنوات عديدة قبل إنشاء الأجهزة العاملة للحوسبة الكمومية. ومع ذلك ، فإن المبادئ العامة لهذا النموذج مفهومة بالفعل اليوم ، فهناك تجريدات تسمح للمطورين بإنشاء تطبيقات تتحقق فيها إمكانيات الحوسبة الكمومية باستخدام أجهزة المحاكاة.

هل يتم تقليل الحوسبة الكمومية إلى مكسب وحدة المعالجة المركزية آخر؟

يتضمن تطوير البرامج التقليدية باستخدام أجهزة الكمبيوتر الكلاسيكية ترجمة لغة برمجة عالية المستوى (على سبيل المثال ، Java) إلى عمليات يتم تنفيذها على عدد كبير من الترانزستورات (الأجهزة).

في الشكل 1 ، يتم تخطيط هذه العملية بأبسط أشكالها: يتم تجميع شفرة مصدر Java إلى شفرة بايت مستقلة عن النظام الأساسي ، والتي بدورها تُترجم إلى رمز آلة خاص بالمنصة. يستخدم رمز الجهاز عددًا من العمليات البسيطة (البوابات) التي تتم في الذاكرة. المكون الرئيسي للأجهزة المستخدمة لهذا الغرض هو الترانزستور المعروف.



التين. 1. ترجمة لغة برمجة عالية المستوى إلى عمليات تتم على الترانزستورات .

تم تحقيق زيادة في الإنتاجية التي تحققت في السنوات الأخيرة بشكل رئيسي بسبب تحسين تقنيات الأجهزة. انخفضت أحجام الترانزستور الفردي بشكل كبير ، وكلما زاد عدد الترانزستورات التي يمكنك وضعها على كل ملليمتر مربع ، زادت مساحة الذاكرة والمعالجة في الكمبيوتر.

الحوسبة الكمومية هي تقنية تخريبية ، لأن أبسط وحدات الحوسبة هنا ليست الترانزستورات الكلاسيكية ، ولكن الكبتات ، والتي سنتحدث عنها أدناه.

النقطة ليست فقط في الاختلافات بين هذه العناصر الأساسية ، ولكن أيضا في جهاز مختلف من الصمامات. وهكذا ، المكدس مع التين. 1 في الحوسبة الكمومية لا ينطبق.

هل ستؤدي الحوسبة الكمومية إلى كسر الحزمة الكاملة أعلاه إلى مستوى جافا؟

باختصار - "ليس حقًا". يوافق العلماء بالتدريج على أن أجهزة الكمبيوتر الكمومية ستكون مفيدة بشكل خاص في حل مشكلات معينة ، بينما سيتم حل المشكلات الأخرى بطريقة أكثر عقلانية باستخدام أجهزة الكمبيوتر التقليدية. يبدو مألوفا ، أليس كذلك؟ ويلاحظ موقف مماثل عند مقارنة GPU و CPU. في حين تستخدم الترانزستورات أيضًا في وحدة معالجة الرسومات ، إلا أنها تختلف من حيث المبدأ عن وحدة المعالجة المركزية ، ومع ذلك ، فإن العديد من التطبيقات المكتوبة بلغة عالية المستوى تستخدم إمكانيات كل من وحدة المعالجة المركزية ووحدة معالجة الرسومات تحت الغطاء. وحدات معالجة الرسومات جيدة جدًا لمعالجة المتجهات ، وفي العديد من التطبيقات والمكتبات ، يتم التمييز بين عمل وحدة المعالجة المركزية ووحدة معالجة الرسومات.

على سبيل المثال ، هذا هو بالضبط الموقف عند استخدام JavaFX أو Deeplearning4j. إذا كنت تكتب تطبيقًا لواجهة المستخدم باستخدام JavaFX ، فأنت تعمل فقط مع تعليمات Java البرمجية (وربما أيضًا FXML لتعلن واجهة المستخدم). عندما تحتاج إلى عرض مشهد JavaFX على الشاشة ، تستخدم تطبيقات JavaFX الداخلية تظليلات وأنسجة لذلك ، والاتصال مباشرة ببرامج تشغيل GPU ذات المستوى المنخفض ، كما هو مبين في الشكل 2. لذلك ، لا داعي للقلق بشأن أي جزء من الكود يتم تكييفه بشكل أفضل للعمل مع وحدة المعالجة المركزية وأي مع GPU.



التين. 2. JavaFX يفوض عمل GPU و CPU.

كما هو مبين في التين. 2 ، يطبق كود تنفيذ JavaFX العمل عن طريق تمريره إلى وحدة معالجة الرسومات ووحدة المعالجة المركزية. على الرغم من أن هذه العمليات مخفية عن المطور (لا يتم توفيرها من خلال واجهة برمجة التطبيقات) ، إلا أن معرفة معينة بوحدة معالجة الرسومات تكون مفيدة غالبًا عندما تحتاج إلى تطوير تطبيقات JavaFX أكثر قوة.

عند استخدام Deeplearning4j ، يتطور وضع مشابه. يحتوي Deeplearning4j على عدد من التطبيقات لتنفيذ عمليات المتجهات والمصفوفة المطلوبة ، وبعضها يستخدم وحدات معالجة الرسومات. ومع ذلك ، لا يهمك كمطور نهائي القدرات التي ستستخدمها الشفرة - وحدة المعالجة المركزية أو وحدة معالجة الرسومات.

يبدو أن أجهزة الكمبيوتر الكمومية ستقوم بعمل ممتاز في حل المشكلات التي ، كقاعدة عامة ، تزداد أضعافا مضاعفة مع نمو حجم المشكلة ، وبالتالي ، لا يمكن حلها أو حلها تقريبًا باستخدام أجهزة الكمبيوتر التقليدية. على وجه الخصوص ، يتحدث الخبراء عن تجسيد هجين: يحتوي التطبيق الشامل من طرف إلى طرف على شفرة كلاسيكية يتم تشغيلها على وحدة المعالجة المركزية ، ولكن قد تحتوي أيضًا على شفرة كمومية.

كيف يمكن لنظام تنفيذ كود الكم؟

اليوم ، لا تزال أجهزة الكمبيوتر الكمومية تجريبية للغاية. في حين أن الشركات الكبيرة ، ومن المفترض أن بعض الدول تشارك في تطوير نماذج أولية ، فإن هذه التكنولوجيا ليست متاحة على نطاق واسع. ولكن عندما يظهر ، قد يكون شكله مختلفًا:

• يمكن دمج المعالج الثانوي الكمي مع وحدة المعالجة المركزية في النظام.
• يمكن تفويض المشكلات الكمومية إلى الأنظمة السحابية الكمومية.

على الرغم من أنه لا يزال هناك قدر كبير من عدم اليقين بشأن الخلفية العملية لمثل هذه القرارات ، فإننا نتفق بشكل متزايد على الطريقة التي ينبغي أن تبدو بها الكود الكمي. عند أدنى مستوى يجب أن يكون الطوب الآتي: البتات والبوابات الكمومية . بناءً عليها ، يمكنك إنشاء أجهزة محاكاة الكم التي تنفذ السلوك المتوقع.

لذلك ، يعد محاكاة الكم أداة مثالية لمثل هذا التطور.
يجب أن تكون النتائج التي يقدمونها هي نفسها تقريبًا كما سيتم الحصول عليها على أجهزة حقيقية للكمبيوتر الكمومي - لكن المحاكاة تعمل بشكل أبطأ ، نظرًا لأن التأثيرات الكمومية التي تسرع أجهزة الكم يجب أن تُحاكى باستخدام البرامج التقليدية.

ما هي اللبنات الأساسية للحوسبة الكمومية؟

غالبًا ما يكون من المهم مقارنة الحسابات الكلاسيكية مع الحسابات الكمومية. في الحوسبة الكلاسيكية ، لدينا وحدات صغيرة وبوابات.

تحتوي البتة على جزء واحد من المعلومات ، وقد تكون قيمتها 0 أو 1.
يعمل الصمام على واحد أو أكثر من البتات ويمكن أن يعمل عليها. على سبيل المثال ، يعكس صمام NOT ، الموضح في الشكل 3 ، قيمة البتة. إذا كان الإدخال 0 ، فسيكون ناتج بوابة NOT 1 والعكس صحيح.



التين. 3. لا صمام

في الحوسبة الكمومية ، لدينا وحدات وبوابات مكافئة. المكافئ الكمى للبت هو الكبت. يمكن أن تكون قيمة الكويبت تساوي 0 أو 1 ، مثل البتة الكلاسيكية ، ومع ذلك ، يمكن أن تكون أيضًا في ما يسمى بالتراكب. هذا مفهوم معقد ، حيث يمكن أن يكون الكوابت في نفس الوقت في كلتا الحالتين: 0 و 1.

عندما يكون qubit في حالة تراكب ، تكون قيمته عبارة عن مجموعة خطية من الحالات 0 و 1. يمكن كتابة ذلك كما هو موضح في الشكل. 4:



التين. 4. المساواة حيث qubit في تراكب.

ملاحظة: غالبًا ما يتم كتابة البتات في ترميز الأقواس ، حيث يتم وضع اسم المتغير بين الأحرف "|" و ">".

التعبير في الشكل. 4 تقارير تفيد بأن qubit x في تراكب الحالات | 0> و | 1>. هذا لا يعني أنه في الحالة | 0> أو في الحالة | 1>؛ هذا يعني أن حالته الحالية غير معروفة لنا.

في الواقع ، إنه موجود في كلتا الولايتين في نفس الوقت ، وفي هذا الشكل يمكن التلاعب به. ومع ذلك ، عندما نقيس qubit ، سيكون في حالة واحدة ، إما | 0> أو | 1>. يوجد قيد آخر في التعبير أعلاه: a ^ 2 + b ^ 2 = 1.
قيم a و b احتمالية: هناك احتمال ^ 2 ، عندما نقيس qubit | x> ، سوف يحتوي على القيمة | 0> ، والاحتمال b ^ 2 الذي سيحتوي qubit المقاسة على القيمة | 1>.

هناك عامل مقيد مهم يكسر أفراح الحوسبة الكمومية: بعد قياس البادئة ، تُفقد جميع المعلومات حول التراكب المحتمل الذي توجد فيه. يمكن أن تكون قيمة qubit 0 أو 1.

في العمليات الحسابية ، يمكن أن تتطابق قيمة البتات في التراكب مع 0 و 1 في نفس الوقت (مع احتمالات مختلفة). إذا كان لدينا اثنين من وحدات البت ، فيمكن استخدامها لتمثيل أربع حالات (00 و 01 و 10 و 11) ، مرة أخرى ، مع احتمالات مختلفة. هنا نأتي إلى جوهر قوة أجهزة الكمبيوتر الكم. امتلاك ثماني بتات كلاسيكية ، يمكنك تمثيل رقم واحد بالضبط في النطاق من 0 إلى 255. وستكون قيم كل من البتات الثمانية هي 0 أو 1. وبعد ثمانية بتات ، يمكنك تمثيل جميع الأرقام في وقت واحد من 0 إلى 255.

ما هو استخدام التراكب إذا كنت تستطيع قياس دولة واحدة فقط؟

غالبًا ما تكون نتيجة الخوارزمية بسيطة (نعم أو لا) ، ولكن للوصول إليها ، هناك حاجة إلى الكثير من الحوسبة المتوازية. مع الاحتفاظ بتراكم في تراكبات أثناء العمليات الحسابية ، يمكنك أن تأخذ في الاعتبار على الفور أي العديد من الخيارات المختلفة. بدون تنفيذ القرارات الخاصة بكل تركيبة فردية ، يمكن للكمبيوتر الكمومي حساب جميع الخيارات في خطوة واحدة.
ثم ، في العديد من الخوارزميات الكمومية ، تبدأ المرحلة المهمة التالية: توصيل نتيجة الخوارزمية بقياس يعطي نتيجة ذات معنى. غالبًا ما يتم أخذ التداخل في الاعتبار: يتم تثبيت النتائج المهمة بشكل هيكلي على بعضها البعض ، بينما تلغي النتائج غير المثيرة للاهتمام بعضها البعض (التداخل المدمر).

كيف يمكن للمرء أن "يحول" qubit إلى حالة تراكب؟

مثلما تعالج البوابات الكلاسيكية البتات ، تتعامل البوابات الكمومية مع الببتات. تشبه بعض البوابات الكمومية الكلاسيكية. على سبيل المثال ، بوابة Pauli-X تنقل qubit من الحالة a | 0> + b | 1> إلى الحالة b | 0 | + a | 1> ، والذي يشبه مبدأ NOT بوابة الكلاسيكية. في الواقع ، عندما تكون a = 1 و b = 0 ، كانت البداية في الحالة | 0>. بعد عمل صمام Pauli-X ، سوف يدخل هذا الكبت في الحالة | 1> ، كما هو مبين في الشكل. 5.



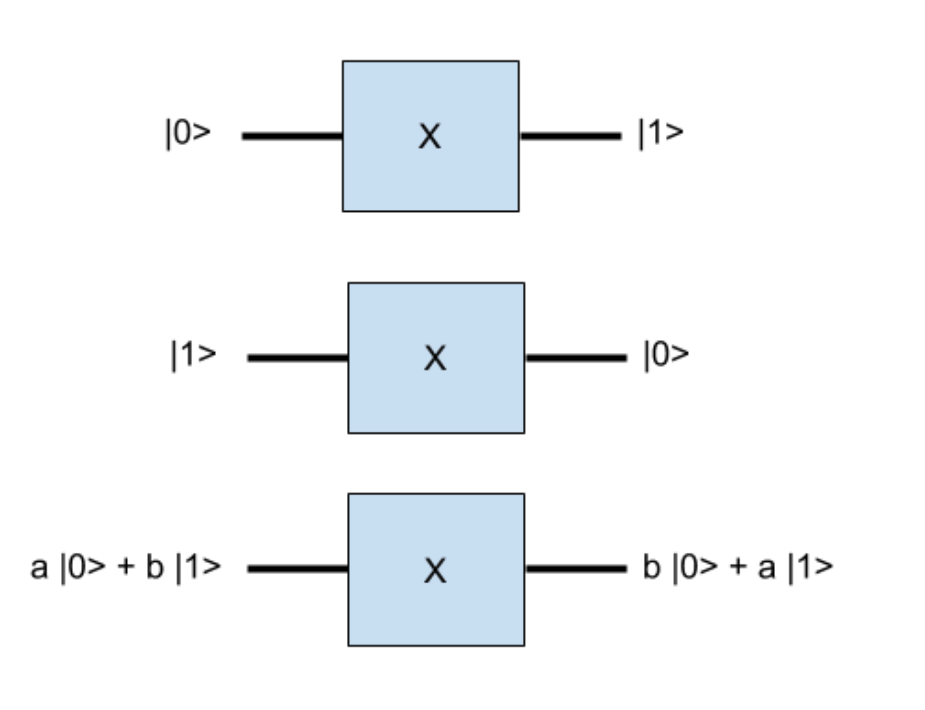التين. 5. نتيجة استخدام صمام Pauli-X.

في هذا السياق ، يعد صمام هادامارد ممتعًا للغاية. يضع البادئة في الحالة | 0>: 1 / sqrt (2) * (| 0> + | 1>) في تراكب ، كما هو مبين في الشكل. 6.



التين. 6. نتيجة تطبيق صمام Hadamard.

بعد تطبيق صمام Hadamard على الكوبيت وقياس الكوبيت ، هناك احتمال بنسبة 50 ٪ أن تكون قيمة الكوبيت 0 و 50 ٪ أن قيمة الكوبيت هو 1. حتى يتم قياس الكوبيت في حالة تراكب .

كيف كل هذا ممكن؟

إذا كنت مهتمًا حقًا بالإجابة على هذا السؤال ، فسيتعين عليك دراسة فيزياء الكم بالتفصيل. لكن لحسن الحظ ، ليس من الضروري فهم الأساس النظري الكامل لهذه الظواهر. في حين أن ظاهرة التراكب قد تبدو غير مفهومة ، من المهم التأكيد على أن هذه الخصائص هي الخصائص المميزة للجزيئات الأولية في الطبيعة. لذلك ، تعد الحوسبة الكمومية أقرب إلى أساسيات الواقع المادي مما تبدو للوهلة الأولى.

هل يجب أن أنتظر بضع سنوات ، ثم ألق نظرة فاحصة على الحوسبة الكمومية؟

لا. في هذه الحالة ، سوف تكون متأخرا. من الممكن نظريًا تطوير الأجهزة أولاً ، ثم متابعة دراسة مستوى البرنامج ومعرفة ما يمكن تحقيقه به. ومع ذلك ، فإن جميع المفاهيم واضحة بالفعل إلى حد ما ، ومن الممكن بالفعل كتابة أجهزة محاكاة الكم في اللغات الشائعة ، بما في ذلك Java و C # و Python وغيرها.
ثم يمكن استخدام هذه المحاكاة للعمل على خوارزميات الكم. على الرغم من أن هذه الخوارزميات لن تعطي زيادة في الأداء يمكن تحقيقها من خلال مساعدتهم عند العمل على أجهزة كمومية حقيقية ، إلا أنها يجب أن تكون كاملة وظيفيًا بالكامل.

وبالتالي ، إذا كنت تقوم حاليًا بتطوير خوارزمية كمية ، فلديك وقت لتحسينها ، ويمكنك تشغيلها عندما تظهر أجهزة الكم في الوصول.

تتطلب الخوارزميات الكمية مقاربة فكرية مختلفة عن النهج التقليدية. بدأ العلماء البارزون في تطوير خوارزميات الكم مرة أخرى في القرن الماضي ، والآن يتم نشر المزيد والمزيد من المقالات التي تصف هذه الخوارزميات ، بما في ذلك تلك المتعلقة بضرب الأعداد الصحيحة ، والبحث في القوائم ، وعمل تحسين المسار ، وأكثر من ذلك بكثير.

هناك أسباب أخرى تجعل الأمر يستحق القيام بالحوسبة الكمومية اليوم. إعادة تشكيل نظام برمجيات في شركة كبيرة حديثة ليست واحدة من تلك الأشياء التي يمكن القيام بها بين عشية وضحاها. ومع ذلك ، فإن التشفير هو أحد المجالات التي ستحدث فيها الحوسبة الكمومية ثورة حقيقية ؛ بعد كل شيء ، كل هذا يعتمد على النظرية القائلة بأنه على الكمبيوتر الكلاسيكي من المستحيل عملياً تحليل عدد صحيح كبير إلى عوامل أولية.

على الرغم من أن الأمر قد يستغرق سنوات عديدة قبل أن تصبح أجهزة الكمبيوتر الكمومية كبيرة بما يكفي لحل مشكلة عامل الأعداد الصحيحة بسهولة ، إلا أن المطورين يعرفون أن الأمر يحتاج إلى سنوات عديدة لتغيير الأنظمة وإدخال تقنيات جديدة أكثر أمانًا فيها.

كيف يمكنني تعلم العمل مع خوارزميات الكم في جافا؟

يمكنك تنزيل إتقان Strange ، محاكي الكمبيوتر الكم المفتوح المصدر في Java. يتيح لك Strange محاكاة خوارزمية كمومية من خلال إنشاء سلسلة من البتات وتطبيق عدة بوابات كمومية عليها.

كمثال بسيط ، فلننشئ اثنين من البتات ، q [0] و q [1] ، بحيث يكون كلاهما مبدئيًا في الحالة 0. ثم نطبق بوابتين بسيطتين على كل من البتات ، بحيث تتوافق هذه العملية مع الشكل. 7.

سوف يذهب الكبت الأول أولاً إلى صمام Pauli-X ، ثم إلى صمام Hadamard. سيقوم صمام Pauli-X بترجمته من الحالة | 0 & gt إلى | 1 & gt ، وسيقوم صمام Hadamard بترجمته إلى تراكب باحتمالات متساوية | 0 & gt و | 1 & gt. لذلك ، إذا أكملنا التسلسل بأكمله 1000 مرة وقاسنا أول مرة 1000 مرة في نهاية هذه الدورة ، في المتوسط ​​يمكننا أن نتوقع أنه في 500 حالة سيكون لها قيمة 0 وفي 500 حالة سيكون لها قيمة 1.

و qubit الثاني هو أبسط. نبدأ مع بوابة الهوية ، والتي لا تغير سلوك البتات ، ثم نمررها إلى بوابة Pauli-X ، مع تغيير قيمتها من 0 إلى 1.



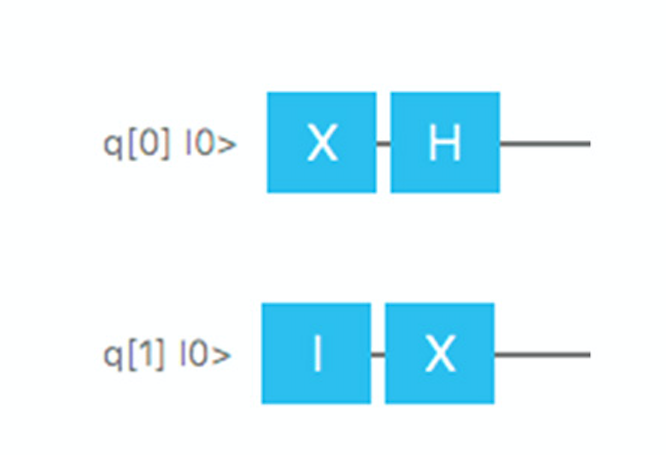التين. 7. مثال على خوارزمية الكم التي يمكن محاكاةها باستخدام غريب.

للتأكد من صحة منطقنا ، يمكنك إنشاء برنامج كم بسيط باستخدام Strange.

public static void main(String[] args) { Program p = new Program(2); Step s = new Step(); s.addGate(new X(0)); p.addStep(s); Step t = new Step(); t.addGate(new Hadamard(0)); t.addGate(new X(1)); p.addStep(t); SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment(); Result res = sqee.runProgram(p); Qubit[] qubits = res.getQubits(); Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure())); } 

في هذا التطبيق ، يتم إنشاء برنامج كم مع اثنين من وحدات البت:

  Program p = new Program(2); 

كجزء من هذا البرنامج ، نمر بمرحلتين. في الخطوة الأولى ، قم بتطبيق صمام Pauli-X على q [0]. لا نطبق الصمام على q [1] ، وبالتالي يعني أنه سيعمل مع صمام الهوية. أضف هذه الخطوة إلى البرنامج:

  Step s = new Step(); s.addGate(new X(0)); p.addStep(s); 

ثم نذهب إلى المرحلة الثانية ، حيث نطبق صمام Hadamard على q [0] وصمام Pauli-X على q [1] ؛ أضف هذه الخطوة إلى البرنامج:

  Step t = new Step(); t.addGate(new Hadamard(0)); t.addGate(new X(1)); p.addStep(t); 

لذلك ، برنامجنا جاهز. الآن دعونا نفعل ذلك. تم بناء محاكي الكم في Strange ، ومع ذلك ، يمكن لـ Strange أيضًا استخدام خدمة سحابية لتشغيل البرامج في نوع من السحابة ، على سبيل المثال ، في Oracle Cloud .

في المثال التالي ، نستخدم محاكيًا مدمجًا بسيطًا ، ونشغل البرنامج ، ونحصل على البتات الناتجة:

  SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment(); Result res = sqee.runProgram(p); Qubit[] qubits = res.getQubits(); 

قبل أن نقيس وحدات البت (ونفقد كل المعلومات) ، نعرض الاحتمالات. الآن قم بقياس وحدات البت ونظر إلى القيم:

 Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure())); 

تشغيل هذا التطبيق ، نحصل على الإخراج التالي:

qubit with probability on 1 = 0.50, measured it gives 1
qubit with probability on 1 = 1, measured it gives 1
يرجى ملاحظة: بالنسبة للكمبيت الأول ، يمكن أيضًا قياس القيمة 0 ، كما توقعنا.
إذا قمت بتشغيل هذا البرنامج عدة مرات ، فستكون قيمة البايت الأول في المتوسط ​​0 في نصف الحالات وواحدة في نصف الحالات.

هل هذا كل ما تحتاج لمعرفته حول الحوسبة الكمومية؟

بالطبع لا. هنا لم نتطرق إلى عدد من المفاهيم المهمة ، على وجه الخصوص ، لم نناقش التعقيدات التي تضمن التفاعل بين اثنين من البتات ، حتى لو كانت جسديا بعيدة كل البعد عن بعضها البعض. لم نتحدث عن خوارزميات الكم الأكثر شهرة ، من بينها خوارزمية Shore ، والتي تسمح بتحليل الأعداد الصحيحة إلى عوامل أولية. تجاهلنا أيضًا عددًا من الحقائق الرياضية والفيزيائية ، على وجه الخصوص ، لم نأخذ في الاعتبار أنه في التراكب | x> = a | 0> + b | 1> ، يمكن أن يكون كلا الرقمين a و b معقدًا.

ومع ذلك ، كان الغرض الرئيسي من هذه المقالة هو إعطاؤك انطباعًا عن الحوسبة الكمومية وفهم مدى ملاءمتها لمستقبل تطوير البرمجيات.