مرحبا يا هبر!
بدا هذا المنشور مثيراً للاهتمام بالنسبة لي:
لقد حصلنا على
أسعار صرف مطلقة من أسعار صرف العملات المتزاوجة وأردت اختبار القدرة على العثور على سعر صرف aaaabsolute هذا من خلال النمذجة الرقمية ، والتخلي عمومًا عن الجبر الخطي.
وكانت النتائج مثيرة للاهتمام.
ستكون التجربة صغيرة: 4 عملات ، 6 أزواج عملات. لكل زوج ، قياس مسار واحد.
لذلك دعونا نبدأ
الفرضية هي أنه يمكن التعبير عن قيمة أي عملة بقيمة معينة تأخذ في الاعتبار قيمة العملات الأخرى التي يتم نقلها بها ، بينما سيتم التعبير عن العملات الأخرى نفسها بقيمة جميع العملات الأخرى. هذه مهمة تكرارية مثيرة للاهتمام.
هناك 4 عملات:
بالنسبة لهم ، تم طلب أزواج العملات:
- اليورو مقابل الدولار الأميركي
- الجنيه الإسترليني مقابل الدولار
- اليورو مقابل الفرنك السويسري
- اليورو مقابل الجنيه الإسترليني
- GBPCHF
- الدولار مقابل الفرنك السويسري
يرجى ملاحظة أنه إذا كان عدد العملات هو n = 4 ، فإن عدد الأزواج هو k = (n ^ 2 - n) / 2 = 6. ليس من المنطقي البحث عن usdeur إذا تم اقتباس eurusd ...
في الوقت t ، تم قياس سعر الصرف لأحد مقدمي الخدمات:
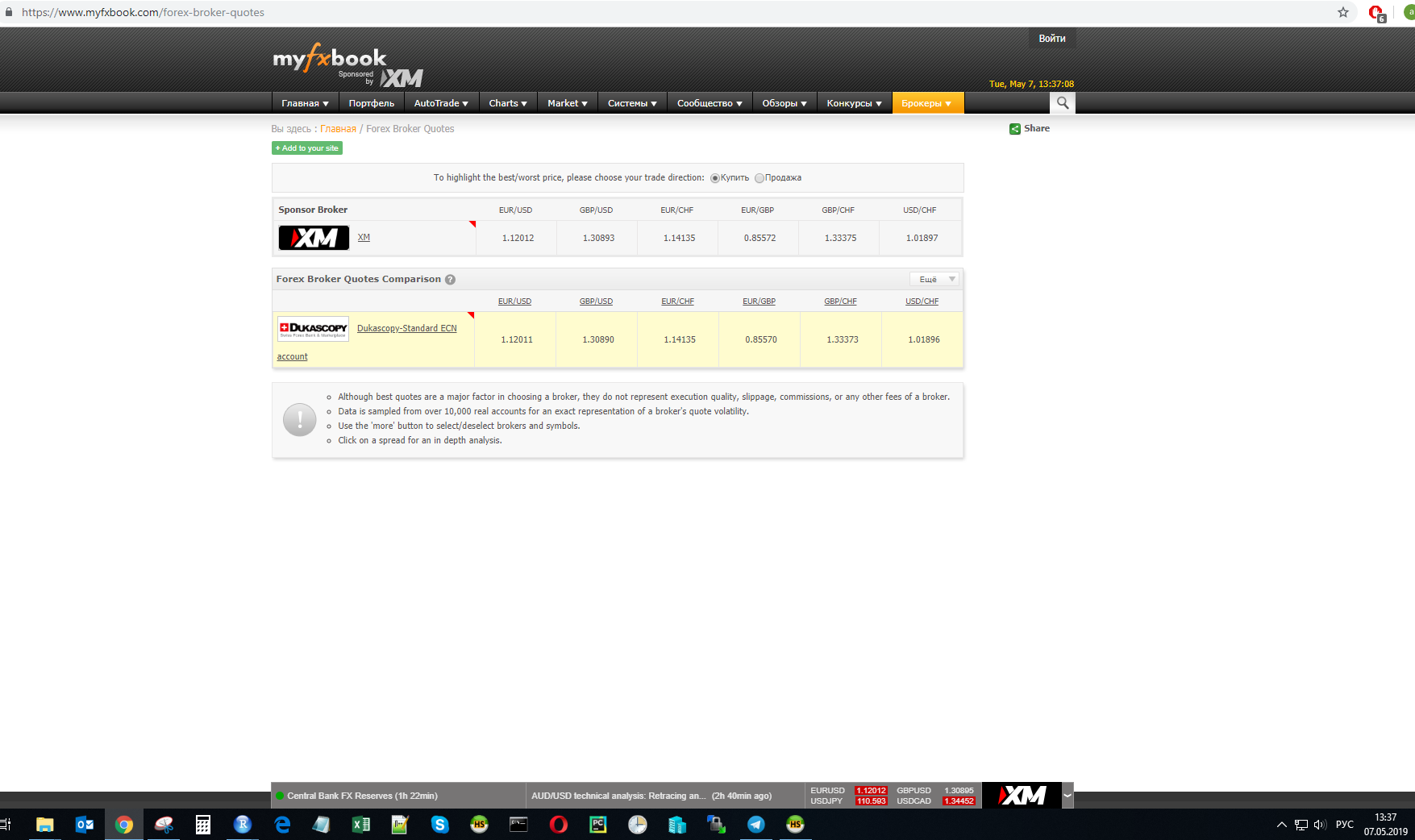
سيتم تنفيذ الحسابات لهذه القيم.
الرياضيات
أتمكن من حل المشكلة عن طريق أخذ تدرج دالة الخسارة بشكل تحليلي ، وهو نظام المعادلات بشكل أساسي.
سيكون رمز التجربة باللغة R:
R يسمح باستخدام stats :: D لأخذ مشتق من دالة. على سبيل المثال ، إذا كنا نريد التمييز حسب عملة الدولار الأمريكي ، فسوف نحصل على التعبير:
2 * (eur / usd ^ 2 * (eurusd - eur / usd)) + 2 * (gbp / usd ^ 2 * (gbpusd -
gbp / usd)) - 2 * (1 / chf * (usdchf - usd / chf))
لتقليل قيمة الدالة Express ، سنؤدي إلى نزول التدرج ومن الواضح على الفور (نرى اختلافات مربعة) أن الحد الأدنى للقيمة سيكون صفرًا ، وهو ما نحتاجه.
-deriv_vals * lr
سيتم التحكم في خطوة نزول التدرج بواسطة المعلمة lr ويتم أخذ كل ذلك بعلامة سالبة.
وهذا يعني ، بكلمات بشرية ، تحديد أسعار 4 عملات بحيث تتلقى جميع أزواج العملات في التجربة قيمًا مساوية للقيم الأولية لهذه الأزواج. ط ط ط ، دعونا حل اللغز - في الجبهة!
النتائج
حتى لا تمدد ، سأخبرك فورًا بما يلي: التجربة ككل كانت ناجحة ، تم تنفيذ الشفرة ، اقترب الخطأ ، بالقرب من الصفر. ولكن بعد ذلك لاحظت أن النتائج مختلفة دائما.
سؤال للخبراء: يبدو أن هذه المهمة لها عدد غير محدود من الحلول ، لكن في هذا ، أنا صفرية كاملة ، أعتقد أنهم سيخبرونني في التعليقات.
للتحقق من استقرار (un) الحل ، قمت بمحاكاة 1000 مرة دون إصلاح بذرة PRNG لقيم البدء في قيم العملات.
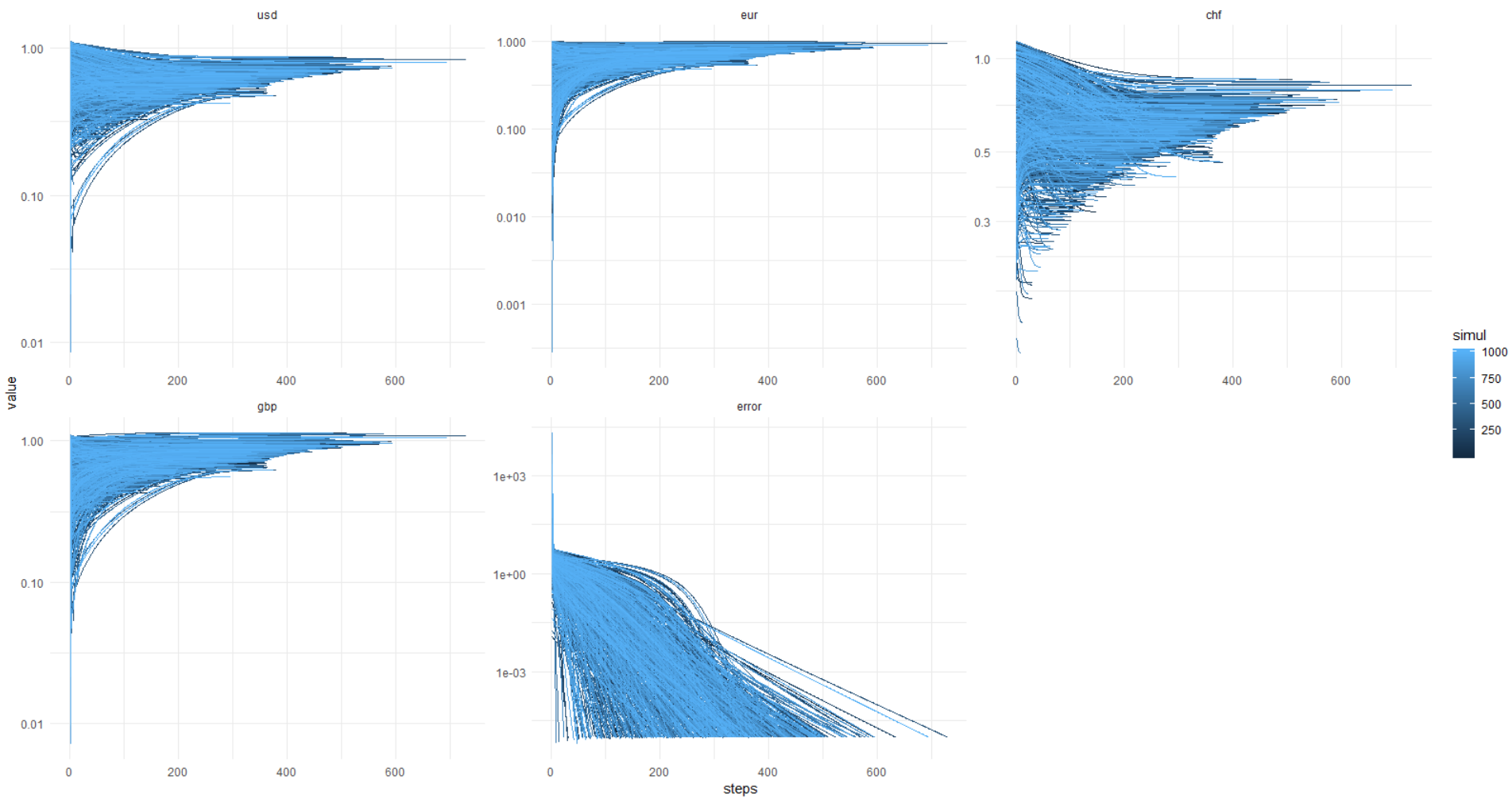
وهنا تأتي الصورة من الكاتا: يصل الخطأ إلى 0.00001 وأقل (يتم ضبط التحسين بهذه الطريقة) دائمًا ، في حين أن قيم العملات تطفو الشيطان ، تعرف أين. اتضح أن هناك دائما قرار مختلف ، أيها السادة!
مرة أخرى ، هذه الصورة ، المحور ص في الوحدات الأصلية (وليس تسجيل الدخول):
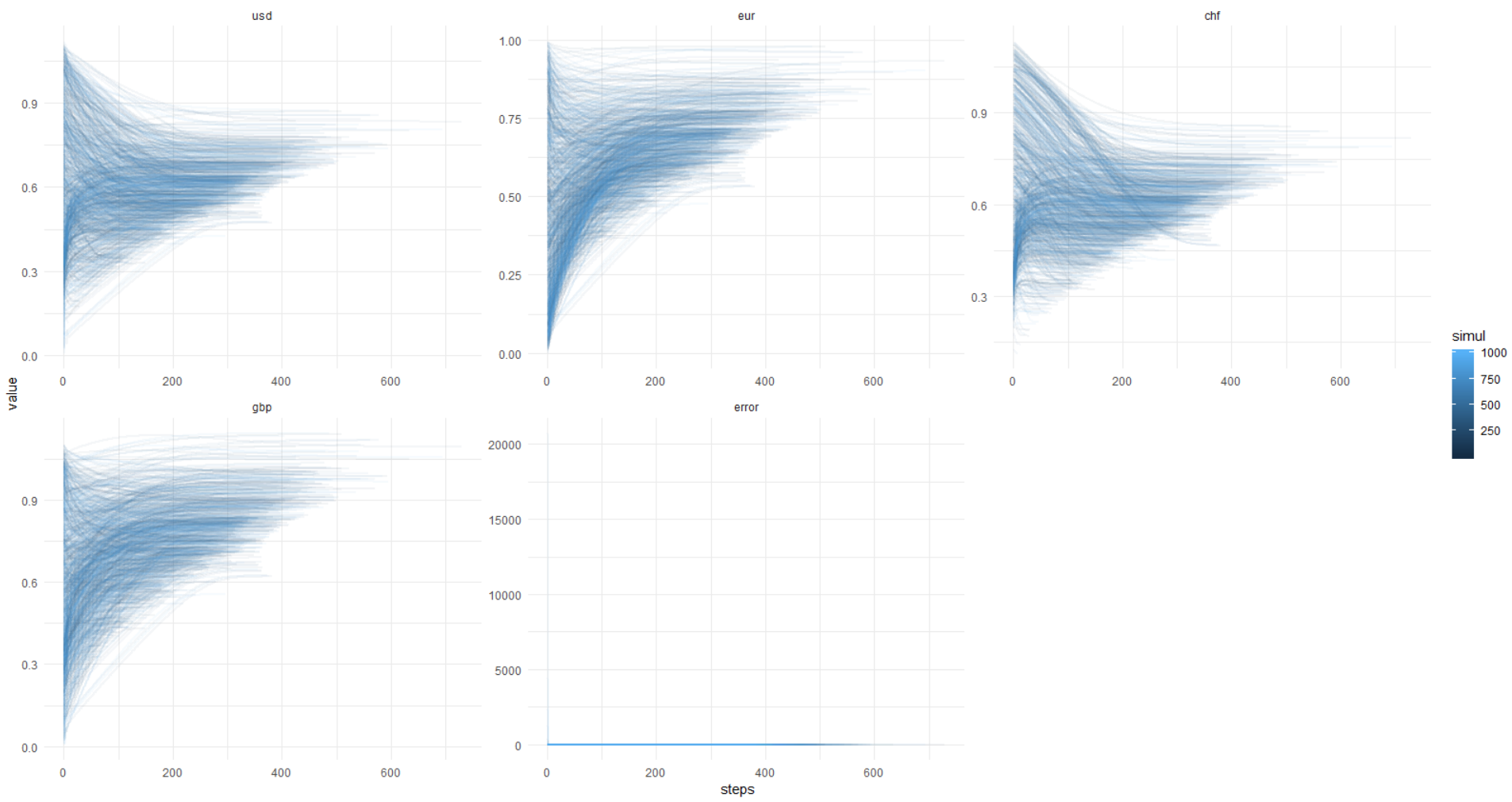
حتى تتمكن من تكرار هذا ، أرفق أدناه الرمز الكامل.
يعمل رمز 1000 محاكاة لمدة دقيقة تقريبًا.استنتاج
هنا ما زال غير واضح بالنسبة لي:
- هل من الممكن تثبيت الحل بطريقة رياضية صعبة؟
- ما إذا كان هناك تقارب مع المزيد من العملات وأزواج العملات ؛
- إذا لم يكن هناك استقرار ، فبالنسبة لكل لقطة بيانات جديدة ، ستعمل عملاتنا كما يحلو لهم ، إذا لم تقم بإصلاح بذرة PRNG ، وهذا هو الفشل.
الفكرة كلها تبدو غامضة للغاية في غياب أي شروط وقيود واضحة. لكنها كانت مثيرة للاهتمام!
حسنًا ، أردت أيضًا أن أقول أنه يمكنك الاستغناء عن OLS عندما تكون البيانات صعبة ، أو أن المصفوفات مفردة ، أو جيدة ، أو عندما تكون النظرية غير معروفة (ehh ...).
شكرا
eavprog على الرسالة الأولية.
وداعا!