مقدمة

بالإضافة إلى مقالتي الأخيرة ، أود أيضًا أن أتحدث عن موضوع MIM ( M ulti U ser) MIMO. لقد سبق أن ذكرت مقالًا شهيرًا جدًا للأستاذ هاردت ، حيث يقترح ، مع زملائه ، خوارزمية لفصل المستخدمين في رابط لأسفل استنادًا إلى طرق خطية ، وهي Block Diagonalization للقناة. تحتوي المقالة على عدد كبير من الاستشهادات ، وهي أيضًا منشور أساسي لأحد واجبات الاختبار. لذلك ، لماذا لا تصنع أساسيات الخوارزمية المقترحة؟

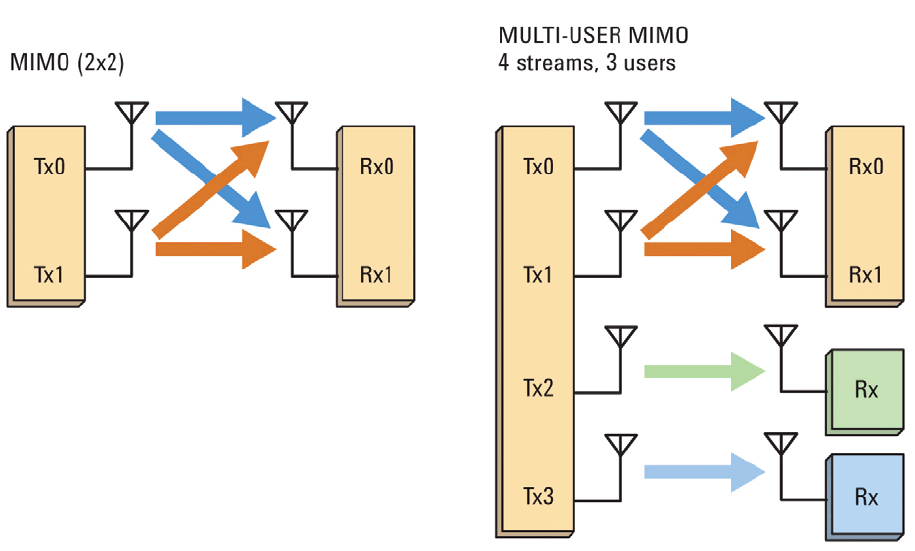
بيان المشكلة

أولاً ، لنقرر في أي مجال في موضوع MIMO سنعمل الآن.
تقليديًا ، يمكن تقسيم جميع أساليب النقل في إطار تقنية MIMO إلى مجموعتين رئيسيتين:

• التنوع المكاني

الهدف الرئيسي هو زيادة مناعة الضوضاء في ناقل الحركة. القنوات المكانية ، إذا كانت مبسطة ، تكرر بعضها البعض ، ونحصل على أفضل جودة نقل.

الأمثلة على ذلك:
- رموز الكتل (على سبيل المثال ، مخطط ألاموتي ) ؛
- رموز تستند إلى خوارزمية Viterbi.

• تعدد الإرسال المكاني

الهدف الرئيسي هو زيادة سرعة النقل. لقد ناقشنا بالفعل في مقال سابق أنه في ظل ظروف معينة ، يمكن اعتبار قناة MIMO كسلسلة من قنوات SISO المتوازية. في الواقع ، هذه هي الفكرة المركزية لتعدد الإرسال المكاني: لتحقيق الحد الأقصى لعدد تدفقات المعلومات المستقلة. المشكلة الرئيسية في هذه الحالة هي قمع التداخل بين القنوات (التداخل بين القنوات) ، والذي توجد فيه عدة فئات من الحلول:

- فصل القناة الأفقية ؛
- عمودي (على سبيل المثال ، خوارزمية V-BLAST) ؛
- قطري (على سبيل المثال ، خوارزمية D-BLAST).

لكن هذا ، بالطبع ، ليس كل شيء.

يمكن توسيع فكرة تعدد الإرسال المكاني: لتقسيم ليس فقط القنوات ، ولكن أيضًا المستخدمين (SDMA - Space Division Multi Access).

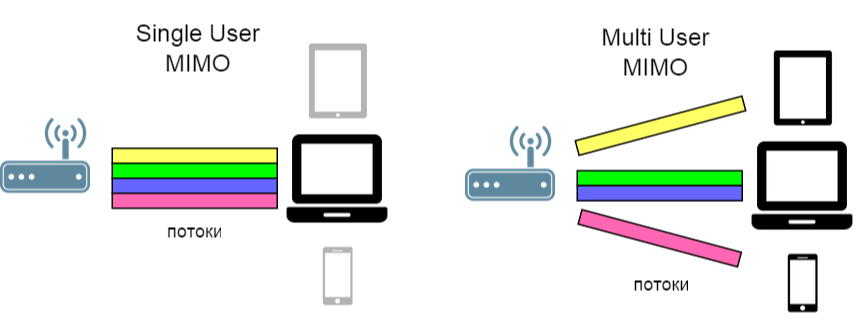
( رابط لمصدر التوضيح )

وبالتالي ، في هذه الحالة ، من الضروري بالفعل مكافحة التداخل بين المستخدمين . لهذا الغرض ، تم اقتراح خوارزمية تدعى Block diagonalization Zero-Forcing ، والتي ندرسها اليوم.

وصف رياضي

لنبدأ ، كما كان من قبل ، بنموذج الإشارة المستلمة. بتعبير أدق ، نعرض على الرسم البياني ما الذي يأتي وماذا يأتي من:

تحتوي مصفوفة القناة في هذه الحالة على الشكل:

مع إجمالي عدد هوائيات الإرسال ، والعدد الإجمالي للهوائيات المستقبلة .

مهم :
لا يمكن تطبيق هذه الخوارزمية إلا بشرط أن يكون عدد هوائيات الإرسال أكبر من أو يساوي إجمالي عدد هوائيات الاستقبال:

هذا الشرط يؤثر مباشرة على خصائص قطري.

لذلك ، يمكن كتابة نموذج الرموز المستقبلة (الإشارات) في شكل متجه على النحو التالي:

ومع ذلك ، من المثير أن ننظر إلى الصيغة لمستخدم معين:

في الواقع:

• هي إشارة مفيدة للمستخدم ك ال ،

  
  

• - هذا هو تدخل من المستخدمين الآخرين ،

  
  

• - الضوضاء المضافة.

لذلك نأتي إلى صياغة المهمة الرئيسية:

يمكنك العثور على هذه المصفوفات بحيث يذهب جزء التدخل إلى الصفر!

هذا هو ما سنفعله.

وصف الخوارزمية

سنقوم بتنفيذ الوصف مع مثال ، وكتوضيح ، سأقدم لقطات شاشة مباشرة ، وأعلق عليها قليلاً.

النظر في المستخدم الأول:

دعنا نتحدث عن الخطوات الرئيسية:

• نصنع بعض المصفوفة من مصفوفات القناة لجميع المستخدمين الآخرين.

• نحن نحللها باستخدام طريقة SVD .

  
  

• في المصفوفة نجد الفضاء الفرعي الضوضاء (فارغة الفضاء الفرعي) - المصفوفة (على سبيل المثال ، كل ما يتجاوز رتبة المصفوفة - تدل على ذلك ).

  
  

• نؤلف من مصفوفة الضوضاء هذه وإقترانها بالهرميت بعض مصفوفة الإسقاط .

  
  

المضي قدما:

• الآن الجزء الأصلي من مصفوفة القناة اضرب بمصفوفة الإسقاط الناتجة .

  
  

• نتحلل النتيجة من خلال SVD.

  
  

• في المصفوفة اختار خطوط أين - رتبة .

  
  

• نقلهم والحصول على المصفوفة (أو - أينما هو مبين).

  
  

وبالتالي سيتم تكرار هذا الإجراء لكل مستخدم. أليس هذا هو سحر الرياضيات: باستخدام أساليب الجبر الخطي ، فإننا نحل المشاكل الفنية تمامًا!

لاحظ أنه في الممارسة العملية ، لا يتم استخدام مصفوفات التشفير المسبق التي تم الحصول عليها فحسب ، بل يتم أيضًا استخدام مصفوفات ما بعد المعالجة ومصفوفة القيم الفردية (انظر الشرائح ). هذا الأخير ، على سبيل المثال ، لموازنة الطاقة وفقًا لخوارزمية صب الماء المعروفة بالفعل.

نحن نموذج الخوارزمية

أعتقد أنه لن يكون من الضروري إجراء محاكاة صغيرة لتعزيز النتيجة. للقيام بذلك ، سوف نستخدم بيثون 3 ، وهي:

import numpy as np 

للحسابات الأساسية ، و:

 import pandas as pd 

لعرض النتيجة.

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF 

لنفترض أن لدينا 8 هوائيات إرسال و 3 مستخدمين لديهم 3 و 2 و 3 هوائيات استقبال ، على التوالي:

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt) 

نحن نهيئ صفنا ونطبق الأساليب المناسبة:

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices() 

نأتي إلى شكل مقروء:

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0 

ودعنا نأخذ قليلاً من أجل الوضوح (على الرغم من أنه يمكنك بدون ذلك):

 print(pd.DataFrame(np.round(np.real(df),100))) 

يجب أن تحصل على شيء مثل هذا:

في الواقع ، ها هم الكتل ، ها هو والتقطير. وتقليل التدخل.

مثل هذه الأشياء.

أدب

1. سبنسر ، كوينتين هـ ، أ. لي سويندلهرست ، ومارتن هارت. "طرق التأثير الصفري لتعدد الإرسال المكاني للوصلة الهابطة في قنوات MIMO متعددة المستخدمين." معاملات IEEE على معالجة الإشارات 52.2 (2004): 461-471.
2. مارتن هارد " معالجة الإرسال القوية لأنظمة MIMO متعددة المستخدمين "

PS

لأعضاء هيئة التدريس والطلاب الأخوة في مهنتي الأم أقول مرحباً!