منذ سنوات عديدة ، كنت أعطي دورات تدريبية في الرسوم التوضيحية والرسوم البيانية لطلاب الرياضيات وعلماء الكمبيوتر (كيف يتم ذلك في اللغة الروسية ، وعلماء الكمبيوتر؟) ، سابقا في الجامعة الأكاديمية ، والآن في
جامعة ولاية سان بطرسبرج . تم تصميم برنامجنا بحيث يتم الاحتفاظ بهذه الموضوعات كجزء من "علوم الكمبيوتر النظرية" (المواضيع الأخرى في ذلك هي الخوارزميات والتعقيد واللغات والقواعد). لا أستطيع أن أقول كيف تم تبرير الميتافيزيقيا أو تاريخيا: ومع ذلك ، فإن الكائنات التوافقية (الرسوم البيانية ، الأنظمة المحددة ، التباديل ، الأشكال المتقلبات ، وما إلى ذلك) بدأت في الدراسة قبل وقت طويل من ظهور أجهزة الكمبيوتر ، والآن الأخيرة ، على الرغم من أهميتها ، أبعد ما تكون عن السبب الوحيد للاهتمام في منهم. لكن النظر إلى المختصين في علم التوافقيات وعلم الكمبيوتر النظري غالبًا ما يكون من المدهش نفس الأشخاص: لوفاس ، ألون ، سميريدي ، رازبوروف وما وراءها. ربما هناك أسباب لذلك. في دروسي ، غالبًا ما يقدم أبطال البرمجة الأولمبيون حلولًا غير تافهة للمشاكل المعقدة (لن أدرجها ، أي شخص لديه فضول لرؤية أفضل الرموز). بشكل عام ، أعتقد أن بعض الأشياء من المجموعات التوافقية قد تهم المجتمع. تحدث إذا كان هناك شيء ما أم لا.
تمكنك من بناء التقليب العشوائي للأرقام من 1 إلى
$ inline $ n $ inline $ بحيث تكون كل التباديل محتملة بنفس القدر. يمكن القيام بذلك بعدة طرق: على سبيل المثال ، أولاً حدد العنصر الأول بشكل عشوائي ، ثم من الثانية المتبقية وما إلى ذلك. أو يمكنك القيام بخلاف ذلك: حدد النقاط بشكل عشوائي
$ inline $ t_1 ، t_2 ، \ ldots ، t_n $ inline $ في هذا الجزء
$ inline $ [0،1] $ inline $ ، وانظر كيف يتم ترتيبها. استبدال أصغر الأرقام بالرقم 1 ، والثاني بالرقم 2 ، وهكذا نحصل على التقليب العشوائي. من السهل أن نرى أن كل شيء
$ inline $ n! $ inline $ التباديل محتمل على قدم المساواة. فمن الممكن وليس في هذا الجزء
$ مضمنة $ 0.1 $ مضمنة اختر نقاطًا ، وعلى سبيل المثال ، بين الأرقام من 1 إلى
$ inline $ n $ inline $ . من الممكن حدوث المصادفات هنا (بالنسبة لشريحة ما ، فهي ممكنة أيضًا ، ولكن باحتمال صفر ، لذلك لا تزعجنا) - يمكنك التعامل معها بطرق مختلفة ، على سبيل المثال ، إعادة ترتيب الأرقام المتزامنة. أو اجعل
N أكبر بحيث يكون احتمال الصدفة صغيرًا (الحالة عندما يكون
$ inline $ N = 365 $ inline $ و
$ inline $ n $ inline $ يوجد عدد الطلاب في الفصل الدراسي الخاص بك ، ونحن نتحدث عن مصادفة اثنين من أعياد الميلاد.) هناك اختلاف في هذه الطريقة: ملاحظة عشوائية
$ inline $ n $ inline $ يشير في مربع وحدة ونرى كيف يتم ترتيب الإحداثيات بالنسبة إلى abscissas. اختلاف آخر: علامة في المقطع
$ مضمنة $ n-1 $ مضمنة $ أشر وانظر كيف يتم ترتيب أطوال الأجزاء التي يتم تقسيمها إليها. النقطة الأساسية في هذه الأساليب هي استقلالية الاختبارات ، وفقًا لنتائج النتائج التي تم فيها إعادة ترتيب عشوائي. قال Andrei Nikolaevich Kolmogorov أن نظرية الاحتمالات هي نظرية للقياس بالإضافة إلى الاستقلال - وهذا سوف يؤكده أي شخص تعامل مع الاحتمال.
سأوضح كيف يساعد ذلك ، وذلك باستخدام مثال
صيغة ربط الأشجار :
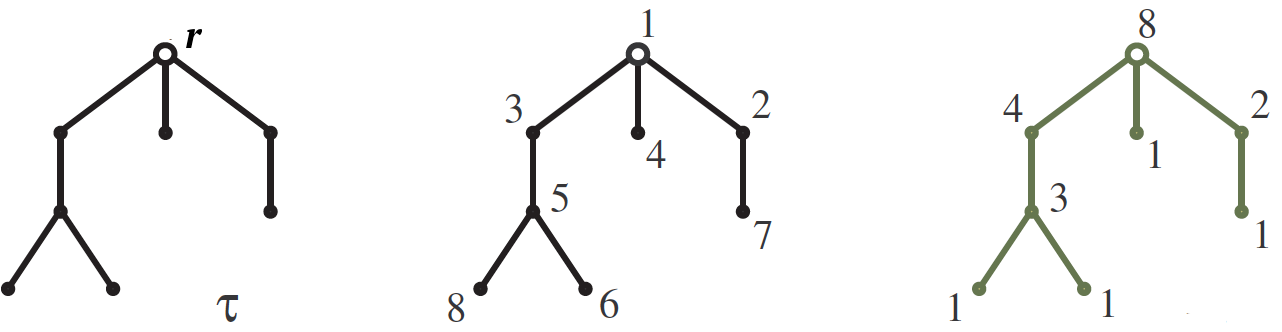
سمح
$ inline $ \ tau $ inline $ - علقت من قبل الجذر
$ مضمنة $ r $ مضمنة $ شجرة مع
$ inline $ n $ inline $ قمم ينمو كما هو الحال في الصورة. هدفنا هو حساب الرقم
$ inline $ S (\ tau) $ inline $ قمم شجرة
الترقيم $ inline $ \ tau $ inline $ الأرقام من 1 إلى
$ inline $ n $ inline $ بحيث يكون الرقم الموجود في قمته لكل حافة أكبر منه في الأسفل. يظهر أحد هذه الأرقام في الصورة الوسطى. تمت صياغة الإجابة باستخدام
أحجام الخطاف . كلاب
$ inline $ H (v) $ inline $ القمم
$ مضمنة $ v $ مضمنة دعنا ندعو شجرة فرعية تنمو من هذه القمة ، وحجمها هو ببساطة عدد القمم الموجودة فيه. تتم كتابة أطوال الخطاف في الصورة اليمنى بجانب الرؤوس المقابلة. لذلك ، فإن عدد الأرقام هو
$ inline $ n! $ inline $ مقسوما على المنتج من أحجام هوك ، لذلك على سبيل المثال لدينا
عرض $$ $$ S (\ tau) = \، \ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $$ display $ $
يمكننا أن نثبت هذه الصيغة بطرق مختلفة ، على سبيل المثال عن طريق الحث على عدد من القمم ، ولكن نظرتنا إلى التباديل العشوائي يسمح لنا بتنفيذ الإثبات دون أي حسابات. من الأفضل ليس فقط من خلال الأناقة ، بل من خلال تعميمها بشكل جيد على الأسئلة الأكثر دقة حول الترقيم مع عدم المساواة المنصوص عليها ، ولكن ليس ذلك الآن. لذا ، خذ أرقامًا حقيقية مختلفة وقم بوضعها عشوائيًا في الجزء العلوي من الشجرة ، ولكل منها رقم واحد ، الكل
$ inline $ n! $ inline $ التباديل محتمل على قدم المساواة. ما هو احتمال أن يكون الرقم الموجود في الجزء العلوي من الحافة أكبر من الرقم الموجود في رأسه السفلي لكل حافة؟ الجواب هو:
$ inline $ S (\ tau) / n! $ inline $ ، ولا يعتمد على مجموعة من الأرقام. وإذا لم يكن الأمر كذلك ، فلننظر إلى الأرقام التي تم اختيارها عشوائيًا أيضًا - للتأكد من دقتها ، في الفاصل الزمني
$ inline $ [0،1] $ inline $ . بدلاً من تحديد الأرقام بشكل عشوائي في البداية ، ثم ترتيبها بشكل عشوائي في أعلى الشجرة ، يمكننا ببساطة اختيار رقم عشوائيًا وبشكل مستقل في كل قمة: ستكون إعادة ترتيبها عشوائية تلقائيًا. بهذه الطريقة
$ inline $ S (\ tau) / n! $ inline $ هذا هو احتمال أن لأرقام مستقلة عشوائية
$ inline $ \ xi (v) $ inline $ اختيار واحد لكل قمة
$ مضمنة $ v $ مضمنة خشب
$ inline $ \ tau $ inline $ ، كل عدم المساواة في النموذج
$ inline $ \ xi (v)> \ xi (u) $ inline $ لجميع الحواف
$ inline $ v \ to $ $ inline .
$ مضمنة $ v $ مضمنة هو قمة الرأس من الضلع ، و
$ inline $ u $ inline $ - القاع. نقوم بصياغة هذه الشروط في شكل مكافئ ، ولكن بطريقة مختلفة قليلاً: لكل قمة
$ مضمنة $ v $ مضمنة يجب أن يحدث مثل هذا الحدث - سأقوم بتعيينه
$ inline $ Q (v) $ inline $ : العدد
$ inline $ \ xi (v) $ inline $ - الحد الأقصى بين جميع الأرقام في رؤوس الشجرة الفرعية هوك
$ inline $ H (v) $ inline $ .
لاحظ ذلك
$ inline $ \ frac {1} {| H (v) |} $ inline $ هذا هو احتمال وقوع حدث
$ inline $ Q (v) $ inline $ . في الواقع ، في الخطاف
$ inline $ H (v) $ inline $ متاح
$ inline $ | H (v) | $ inline $ يتم تعيين الرؤوس والحد الأقصى لعدد الخطاف لكل منهم مع احتمال متساو
$ inline $ \ frac {1} {| H (v) |} $ inline $ . لذلك صيغة هوك
$ inline $ S (\ tau) / n! = \ prod_v \ frac {1} {| H (v) |} $ inline $ يمكن صياغتها على النحو التالي: احتمال حدوث جميع الأحداث دفعة واحدة
$ inline $ Q (v) $ inline $ يساوي نتاج احتمالات هذه الأحداث. قد تكون أسباب ذلك مختلفة كثيرًا ، ولكن السبب الأول الذي يتبادر إلى الذهن يعمل هنا: هذه الأحداث مستقلة. لفهم هذا ، دعونا ننظر ، على سبيل المثال ، في حدث ما
$ inline $ Q (r) $ inline $ (المقابلة للجذر). يتكون في حقيقة أن الرقم في الجذر أكبر من جميع الأرقام الأخرى الموجودة في القمم ، وتتعلق الأحداث الأخرى بمقارنات فيما بينها بالأرقام المكتوبة في الجذر. هذا هو
$ inline $ Q (r) $ inline $ بخصوص الرقم
$ inline $ \ xi (r) $ inline $
ومجموعات الأرقام في رؤوس أخرى ، وجميع الأحداث الأخرى
مرتبة حسب أرقام في رؤوس أخرى غير الجذر. كما ناقشنا بالفعل ، "النظام" و "الجمهور" مستقلان ، وبالتالي الحدث
$ inline $ Q (r) $ inline $ مستقلة عن الآخرين. نزولاً إلى الشجرة ، نتوصل إلى أن كل هذه الأحداث مستقلة عن المكان التالي.
عادةً ما تكون صيغة hooks هي صيغة ترقيم ليس القمم في الشجرة ، ولكن الخلايا في
مخطط Young. 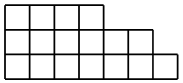
زيادة في اتجاهات محاور الإحداثيات ، والسنانير تشبه السنانير أكثر من الأشجار. ولكن ثبت أن هذه الصيغة أكثر تعقيدا وتستحق وظيفة منفصلة.
منذ أن كان لدي بالمناسبة ، لا يسعني إلا أن أتحدث عن نموذج
لمخطط يونغ عشوائي . مخطط الشباب هو هذا الرقم من
$ inline $ n $ inline $ مربعات الوحدات ، تزداد أطوال صفوفها من الأسفل إلى الأعلى ، وأطوال الأعمدة من اليسار إلى اليمين. عدد من الرسوم البيانية لمنطقة يونغ
$ inline $ n $ inline $ يشار
$ inline $ p (n) $ inline $ ، هذه
الوظيفة الهامة تتصرف بطريقة مثيرة للاهتمام وغير عادية: على سبيل المثال ، تنمو أسرع من أي كثير الحدود ، ولكنها أبطأ من أي الأس. لذلك ، على وجه الخصوص ، إنشاء مخطط يونغ عشوائي (إذا كنا نريد جميع الرسوم البيانية المنطقة
$ inline $ n $ inline $ كانت على الأرجح متساوية
$ inline $ 1 / p (n) $ inline $ ) ليست مسألة تافهة. على سبيل المثال ، إذا قمت بإضافة خلايا واحدة في كل مرة ، واخترت مكانًا لإضافته عشوائيًا ، فسيكون للمخططات المختلفة احتمالات مختلفة (لذلك ، فإن احتمال وجود مخطط ذو خط مفرد يتساوى
$ inline $ 1/2 ^ {n-1} $ inline $ .) اتضح تدبيرا مسليا على الرسوم البيانية ، ولكن ليس موحد. يمكن الحصول على الزي الرسمي على النحو التالي. خذ الرقم
$ inline $ t \ in (0،1) $ inline $ ، لأغراضنا ، الأرقام في المنطقة هي الأنسب
$ inline $ 1- \ mathrm {const} / \ sqrt {n} $ inline $ . لكل منهما
$ inline $ k = 1،2 ، \ ldots $ inline $
النظر في التوزيع الهندسي على الأعداد الصحيحة غير السالبة مع الوسط
$ inline $ t ^ k $ inline $ (أي احتمال العدد
$ inline $ m = 0،1 ، \ ldots $ inline $ يساوي
$ inline $ t ^ {km} (1-t ^ k) $ inline $ ). نختار وفقا لذلك متغير عشوائي
$ inline $ m_k $ inline $ (هناك العديد من الطرق لتنظيم هذا). بشكل عام
$ مضمنة $ k $ مضمنة على الأرجح 0. دعونا نلقي نظرة على مخطط يونغ فيه
$ inline $ m_k $ inline $ الصفوف طول
$ مضمنة $ k $ مضمنة في كل
$ inline $ k = 1،2 ، \ ldots $ inline $ . أسميها
طريقة السفينة لأن المساحة الكلية تساوي
أحيانًا $ inline $ n $ inline $ . إن لم تكن متساوية ، كرر التجربة. متساو فعلا
$ inline $ n $ inline $ انها غالبا ما يكفي إذا اختارت بذكاء
$ inline $ t \ in (0،1) $ inline $ . أدعو القارئ لإثبات أن جميع الرسوم البيانية لمنطقة معينة محتملة بنفس القدر وتقدير عدد الخطوات.