29 مارس 2019 - مايكل تروت ، الباحث الرئيسي
دخول
في ما يسمى "SI الجديد" -
نسخة محدثة من النظام الدولي للوحدات ، والتي ستحدد سبع وحدات أساسية للقياس (الثانية ، المتر ، الكيلوغرام ، الأمبير ، الكلفين ، الخلد ، والشمبيلا) والتي ستدخل حيز التنفيذ في 20 مايو 2019 ، يتحدد من خلال القيم الدقيقة للثوابت المادية الأساسية. نتيجة لذلك ، سيتم في النهاية التعبير عن جميع وحدات SI المذكورة أعلاه (نيوتن ، فولت ، أوم ، باسكال ، إلخ) من حيث الثوابت الأساسية. (أخيرًا ، ستتحكم الفيزياء الأساسية حرفيًا في حياتنا اليومية)
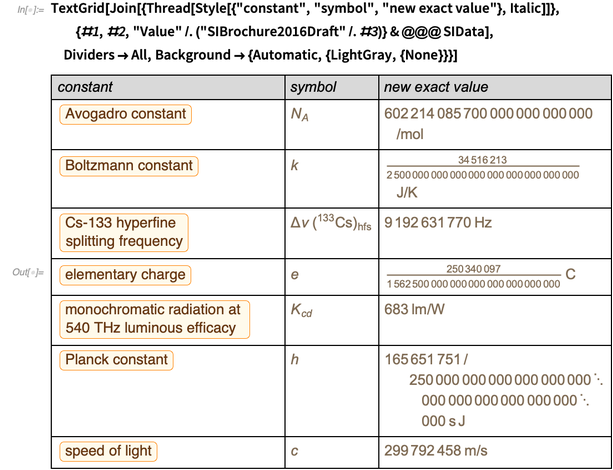
يوضح الجدول أدناه كيف سيتغير كل شيء من مساء الاثنين 20 مايو إلى صباح الثلاثاء 21 مايو من هذا العام.
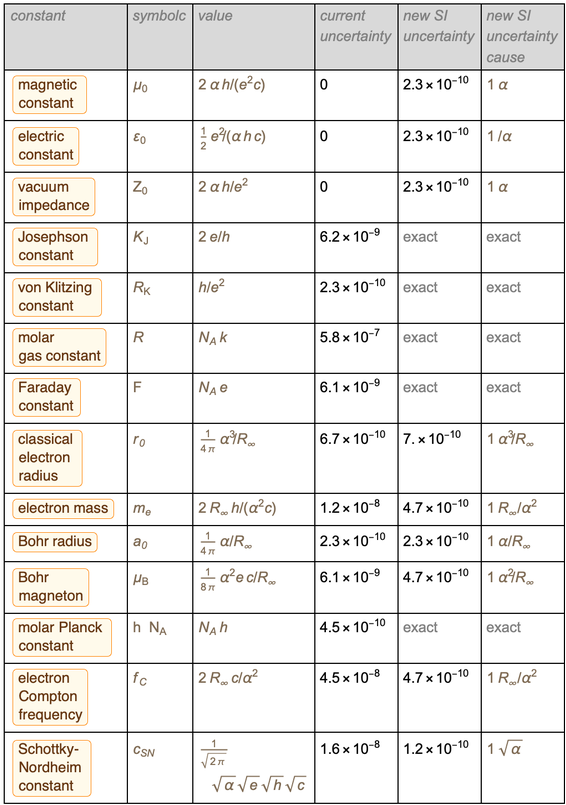
الهدف من هذه المدونة هو حساب البيانات من هذا الجدول. لذلك ، لنبدأ بإلقاء نظرة عامة مختصرة على ما سيتغير في SI الجديد.
بالإضافة إلى القيمة الدقيقة المعروفة لسرعة الضوء ، خلال أربعة أسابيع ، هناك أربعة ثوابت فيزيائية أخرى - ثابت بلانك ، ثابت بولتزمان ، ثابت أفوجادرو وثابت ميليكان (تسمى غالبًا الشحنة الكهربائية الأولية) - ستكون لها قيم دقيقة. تم اتخاذ القرار بشأن هذا التغيير دوليًا في نوفمبر من العام الماضي (كتبت عنه في تقريري الأخير
بلوق).
يوجد أدناه مقتطف من الصفحة 12 من المسودة الحالية
لكتيب SI .
لاحظ أنه في هذه التعريفات ، يُقصد بالأرقام العشرية أنها أرقام عشرية دقيقة ، وليس ، على سبيل المثال ، أرقام الماكينات على جهاز كمبيوتر ذي دقة محدودة وليست أرقامًا دقيقة. تردد الانتقال في بنية رقيق الانقسام Cs-133 ، وسرعة الضوء و "كفاءة الضوء" لديها بالفعل القيم الدقيقة اليوم.
العالم يناقش التغيرات المستقبلية
سيكون لهذا التغيير بعض النتائج المثيرة للاهتمام للثوابت الفيزيائية الأخرى: بعض الثوابت التي يتم قياسها حاليًا والتي تحتوي على أخطاء ستصبح دقيقة ، وبعض الثوابت الدقيقة حاليًا سيكون لها قيم تقريبية مع أخطاء محدودة في المستقبل . هذه التغييرات لا يمكن تجنبها لضمان الاتساق العام للنظام.
تناول العدد الأول
من فيزياء العالم لهذا العام هذا الموضوع في رسالة
إلى رئيس التحرير من ويليام هوغ. لقد كتب:
مع تثبيت الشحنة على الإلكترون ( هـ ) وثابت بلانك ( ح ) ، أصبحت جميع الوحدات الفيزيائية "خلدت الآن في الحجر" ، وهي لطيفة جدًا. لكن هذا يثير سؤالًا محرجًا. هيكل ثابت ثابت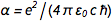 
حيث c هي سرعة الضوء و 
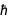إنه كذلك 
. من المعادلات المألوفة 
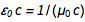و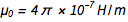 
سرعان ما نجد ذلك 
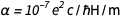. هذا ، بالطبع ، رقم خالص بكمية غير محددة ، وهو ثابت الآن للأبد يساوي 1 / 137.13601 ، وهو قريب جدًا من القيمة المقبولة. هذا ليس مفاجئًا ، حيث سيتم استخدام القيمة الأخيرة في القيم الجديدة المتفق عليها لـ e و ℏ . لكن الطبيعة لها قيمة خاصة بها ، غير معروفة لنا في الوقت الحاضر ، والتي ، بسبب هذا ، خُلدت في الماس. يمكن أن نتسامح بسبب التلميح إلى أننا نعرف أفضل من الطبيعة. ولكن ماذا لو أصبحت نظرية مستقبل الكون مقبولة وتعطي المعنى الدقيق 
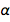وهو يختلف اختلافا كبيرا عن القيمة المقبولة؟ هل يمكن أن يحدث هذا؟ كانت هناك محاولات لإيجاد قيمة نظرية لـ α ، لكنها تشمل تهديد الديناميكيات الكمومية المثيرة للجدل.
المشكلة هي أنه في نظام SI الجديد على حد سواء
و
سيكون لها الآن قيم غير دقيقة مع بعض الأخطاء. في هذه المدونة ، سوف نستخدم لغة Wolfram ومعرفتها بالوحدات المادية والثوابت لمعرفة كيف تكسب هذه الثوابت وغيرها من الثوابت الفيزيائية (أو تفقد) الخطأ ، ولماذا تكون هذه نتيجة رياضية لتعريف الوحدات الأساسية.
لمحة موجزة عن مكونات لغة ولفرام ذات الصلة
لغة Wolfram هي وسيلة فريدة لإجراء تجارب رقمية وحسابات رمزية ، وتحديد العواقب المحتملة. بالإضافة إلى إمكانات الحوسبة العامة ، هناك ثلاثة مكونات للنظام مفيدة جدًا هنا:
1) وحدات لغة Wolfram وهيكل الكميات المادية.
يمكن استخدام الوحدات الكلاسيكية (مثل العدادات والقدمين وما إلى ذلك) في العمليات الحسابية والمرئيات. وبطبيعة الحال ، في تحويل وحدات القياس.
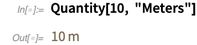
يؤدي التحويل إلى الوحدات الأمريكية العادية إلى كسر (بدلاً من القيمة التقريبية للعدد الحقيقي!) نظرًا للنسب المحددة جيدًا للوحدتين.
يحب الفيزيائيون (خصوصًا) استخدام الوحدات "الطبيعية". غالبًا ما تكون هذه الوحدات الطبيعية مجرد ثوابت فيزيائية أو مجموعات منها. على سبيل المثال ، سرعة الضوء (يتم استخدام إدخال اللغة الطبيعية هنا).
يتم التعبير عنها بوحدات SI (نظرًا لأن هذه السرعة والسرعة بالأمتار والثواني المطلوبة) ، فإن سرعة الضوء لها قيمة دقيقة.
من ناحية أخرى ، ثابت Planck ليس له قيمة محددة حاليًا. وبالتالي ، فإن قيمتها ، معبراً عنها بوحدات الأساس SI ، هي رقم عشري تقريبي.
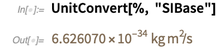
يرجى ملاحظة أن دقة 6.626070 ... تعكس عدد الأرقام المعروفة.
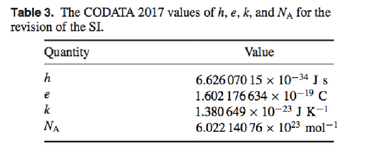
هذه هي القيمة الأخيرة الموصى بها لثابت بلانك المنشورة في
CODATA 2017 استعدادًا لتحسين الثوابت. أدناه هو الجدول المقابل:
غالبًا ما يمكن استخدام الثوابت الفيزيائية (أو مجموعات منها) التي تربط كميتين فيزيائيين كوحدات طبيعية. تتمثل أبسط الأمثلة في قياس السرعة من حيث سرعة الضوء أو عزم الدوران المجهري من حيث
ℏ . أو يمكن قياس الطاقة من حيث الكتلة مع عامل ضمني
. يمكن استخدام وظيفة
DimensionalCombinations للبحث عن مجموعات من الثوابت الفيزيائية التي تسمح لك بربط كميتين ماديتين معينتين. على سبيل المثال ، يمكن بناء العلاقات التالية بين الكتلة والطاقة:
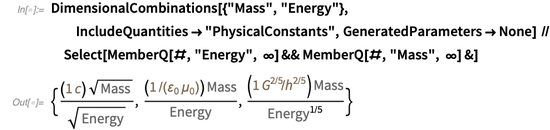
المساواة الأولى تعكس صيغة آينشتاين الشهيرة
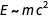
، والثاني هو ما يعادل العلاقة الأولى ، والثالثة - (الأبعاد) التي تنص على ذلك
.
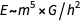
2) تمت إضافة فئة الكيان "
PhysicalConstant " مؤخرًا إلى قاعدة
المعرفة Wolfram .
الوظائف والكائنات في Wolfram Language "يولد حسابيا" ، أي أنها جاهزة للاستخدام في الحوسبة. ولكن لوصف العالم الحقيقي ومحاكاته ، فأنت بحاجة إلى بيانات حول العالم الحقيقي. هيكل الكيان هو وسيلة مريحة ومتكاملة تماما للحصول على هذه البيانات. فيما يلي بعض البيانات عن الإلكترون والبروتون والنيوترون.
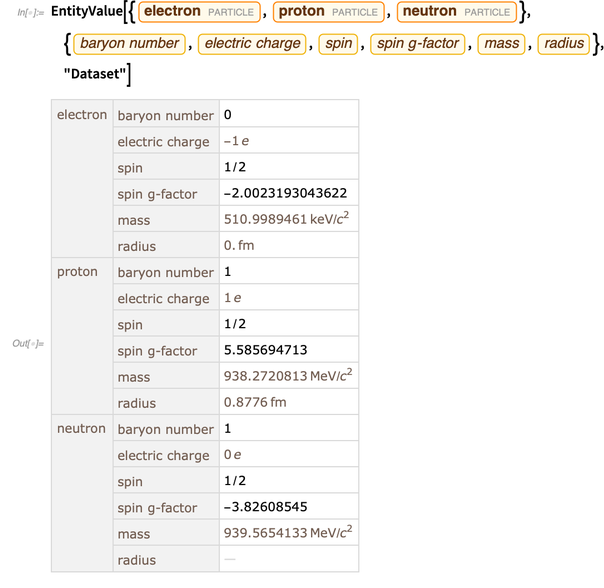
واحدة من وحدات الكيان الجديد هو الثوابت المادية. تحتوي قاعدة المعارف حاليًا على أكثر من 250 من الثوابت الفيزيائية.
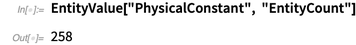
فيما يلي أكثر من عشرة أمثلة تم اختيارها بشكل عشوائي. علاوة على ذلك ، بدون تعريف واضح لما الثوابت هي الثوابت الفيزيائية ، كتل الجسيمات الأساسية ، معلمات لاغرانج للنموذج القياسي ، إلخ. للراحة ، تحتوي القائمة أيضًا على
ثوابت فلكية وفقًا للتقويم الفلكي.
معظم الثوابت الفيزيائية الأساسية كانت تسمى ثوابت الفئة C في
العمل الشهير لجان مارك ليفي لوبلان ، فيما يلي ثوابت الفئة C و B.
خذ على سبيل المثال الوحدة الطبيعية للوقت ، بلانك الوقت.
تسهِّل الدالتان ToEntity و
FromEntity الانتقال ذهابًا وإيابًا بين الثوابت الفيزيائية كوحدات والثوابت المادية ككيانات. يتم عرض كيان يتوافق مع وحدة من وقت بلانك أدناه.
تحتوي قاعدة المعرفة على الكثير من المعلومات الوصفية عنه ، على سبيل المثال ، قيمها في أحدث قوائم CODATA.
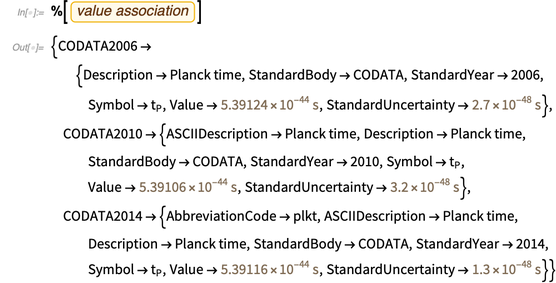
الاستنتاج الأخير ، الذي يحتوي على المعنى والخطأ ، يقودنا إلى الوظيفة المهمة الثالثة ، والتي ستكون مفيدة في وقت لاحق:
3) مقدمة
حول الوظيفة [] في الإصدار 12 من Wolfram Language. توفر الدالة
Around [] قيمة غير دقيقة ، تشير إلى متوسط القيمة والخطأ. يعتمد النموذج الحسابي
حول [] على
GUM (دليل التعبير عن خطأ القياس) - يجب عدم الخلط بينه وبين حساب Leibniz Plus-Minus-calculus. هنا هذه القيمة مع وجود خطأ.
الجانب الأكثر أهمية ومفيدة للحساب مع القيم التي تحتوي على أخطاء هو أنها تأخذ في الاعتبار الارتباطات. إن الاستخدام الساذج لهذه القيم في الأرقام الحسابية أو الفواصل الزمنية يمكن أن يقلل من تقدير الخطأ الناتج أو يبالغ في تقديره.
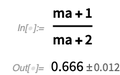
أدناه نرى أن الدالة
AroundReplace [] تأخذ في الاعتبار الارتباط.
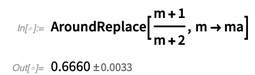
العودة إلى الرسالة إلى المحرر
الآن ، دعونا نستخدم هذه المكونات الثلاثة ورسالة وليام هوغ الأكثر تفصيلاً إلى المحرر.
عند القيم التقريبية الحالية لـ
e و
ℏ ، تكون
هاتان القيمتان لثابتة البنية الدقيقة متناسقة في حدود
أخطائهم . الأول هو التعبير من الرسالة إلى المحرر ، والثاني هو الكمية (
الكمية []) ، والتي تمثل ثابت البنية الدقيقة.
كل بضع سنوات ، تنشر CODATA القيم الرسمية للثوابت الأساسية (انظر
ثوابت البنية الدقيقة ) ؛ كما قلت ، فإن القيم المستخدمة في Wolfram Language هي أحدث قيم CODATA وينعكس الخطأ النهائي في دقة الرقم.
يرجى ملاحظة أن ثابت البنية الدقيقة المقاسة مباشرة أكثر دقة قليلاً من الثابت الذي يعبر عن ثابت البنية الدقيقة من خلال الثوابت الأخرى.
إذا استخدمنا القيم الدقيقة القادمة لـ
e و
ℏ ،
واستخدمنا القيمة الفعلية الحالية
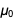
، نحصل على القيمة الدقيقة التالية للهيكل الدقيق الثابت في النموذج
.
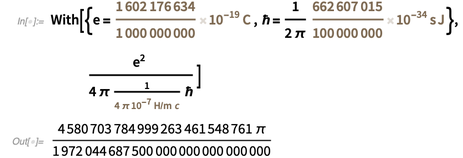
من غير المرجح أن يختار الرب ، الذي لا
يلعب النرد ، مثل هذا الرقم للقيمة
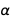
في عالمنا. هذا يعني أنه بينما يتم إصلاح
e و
in في SI الجديد ، فإن القيم الحالية الدقيقة
و
يجب أن يكون "فصل" حتما (انظر أيضا
مقالة Goldfarb على الكمية
SI جديد). (سوف نعود إلى السبب
و
قريبا لتصبح غير دقيقة.)
هذا يعني أنه بعد 20 مايو من هذا العام ، ستكون هذه النتائج مختلفة عن تلك الواردة أدناه.
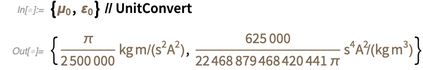
(في ملاحظة موجزة ، قامت فئة الكيان "
PhysicalConstant " أيضًا بتقدير قيم الثوابت ، مثل ثابت البنية الدقيقة):
الآن ، بصرف النظر عن الحجة اللاهوتية حول الشكل الدقيق للبنية الدقيقة الثابتة ، من وجهة نظر مادية ، لماذا
و
يجب أن تكون غير دقيقة؟ كحجة الاحتمال ، دعونا ننظر
. واحدة من أبرز النتائج هو قانون كولوم.
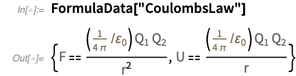
في نظام SI
الحالي ، يكون للأمبير تعريف "دقيق":
الأمبير هو ذلك التيار المباشر ، الذي ، إذا كان مدعومًا في موصلين متوازيين بطول لانهائي مع مقطع دائري طفيف ووضعه على مسافة متر واحد في فراغ ، سيخلق قوة بين هذه الموصلات تساوي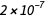 
نيوتن لكل متر طول. يستخدم هذا التعريف كميات ميكانيكية بحتة نيوتن وعدادت (أي بعد التمدد ، هذا ثاني متر و كيلوغرام). لا توجد علاقة مع شحنة الإلكترون ، وفي نظام SI الحالي ، تكون الشحنة الأولية عبارة عن كمية تم قياسها تجريبيًا.
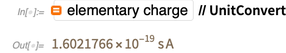
وقد تغيرت هذه القيمة المقاسة تجريبياً على مر السنين ، وأصبحت أكثر دقة.
تحتوي القوة الموجودة على الجانب الأيسر من قانون كولوم (المعبر عنها في نيوتن) على الوحدة الأساسية للكيلوغرام ، والتي ، بعد أن تصبح قيمة ثابت بلانك ثابتة ، تصبح أيضًا محددة بدقة. نظرًا لعدم وجود سبب للاعتقاد بأن جميع قوانين الطبيعة يمكن التعبير عنها بأعداد عقلانية محدودة ، فإن "الجزء المتحرك" الوحيد الممكن في قانون كولوم هو
. يجب تحديد قيمتها العددية ، وستجعل الجانبين الأيسر والأيمن من قانون Coulomb يتزامنان.
من وجهة نظر أكثر جوهرية للفيزياء ، ثابت البنية الدقيقة هو ثابت التفاعل ، الذي يحدد قوة التفاعلات الكهرومغناطيسية. وربما في يوم من الأيام ، يمكن للفيزياء حساب قيمة ثابت البنية الدقيقة ، لكننا لا نزال بعيدين عن هذا. مجرد اختيار تعريفات الوحدة لا يمكن إصلاح القيمة
.
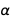
كلاهما حقا
و
تصبح غير مثبتة ، أم أنه من الممكن الحفاظ على دقة أحدهم؟ بسبب سرعة الضوء بالفعل والنسبة
إذا كان أحد
أو
دقيقة ، والآخر يجب أن يكون دقيقا أيضا. نحن نعلم أنه على الأقل يجب أن يصبح المرء غير ملتزم ، لذلك يجب أن يكون كلاهما غير ملتزمين.
القيم التي يتم إعطاءها الآن بواسطة ثابت Planck ، ثابت Boltzmann ، ثابت Avogadro ، والتهمة الأولية ليست تعسفية ولا محددة بالكامل. يتم تحديد ما يصل إلى ثمانية أحرف تقريبًا ، لذا فإن وحدات القياس التي تحددها بعد 20 مايو تتوافق مع "حجم" الوحدات التي تحددها قبل 20 مايو. لكن الأرقام في أسفل اليمين غير محددة. وبالتالي ، يمكن أن تكون قيمة القيمة الدقيقة المستقبلية للرسوم الأولية
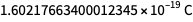
لكن لا
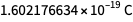
. إنها أداة الحلاقة والعقلانية التي تسمح لنا باستخدامها
.
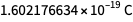
على مستوى أكثر تقنية ، كان الاستبدال في الحساب السابق هو ذلك من خلال المصطلح
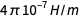
في الصيغة
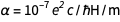تم استخدام أمبير قبل إعادة تعريف (تذكر
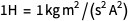
) ، ولكن تم استخدام القيمة الدقيقة للتهمة الأولية أيضًا ، مما يعني تعريف الأمبير بعد إعادة التعريف. ونحن دائما بحاجة إلى البقاء في نظام واحد من الوحدات.
حساب جدول النماذج الأمثل خطأ
لذا ، فإن السؤال الطبيعي الذي يطرح نفسه: ما ينبغي أن تكون هذه المعاني "غير المثبتة"؟ في مدونتي الأخيرة ، قمت يدويًا بإنشاء قيمة جديدة
. ما يمكن القيام به يدويًا يمكن القيام به باستخدام برنامج كمبيوتر ، لذلك دعونا ننفذ برنامجًا صغيرًا يحسب الشكل الأمثل للخطأ لمشتقات الثوابت المادية. في نهج موجه نحو المستقبل ، تتوفر بالفعل فئة كيان مكونة من سبعة ثوابت تعرّف SI جديدة.
فيما يلي الثوابت التي سيكون لها قيمة محددة في SI الجديد.
تحتوي القيم الحالية لهذه الثوابت مع الخطأ الخاص بها (المحسوبة باستخدام الدالة
Around []) على النموذج:
باستخدام فئة الكيان "
PhysicalConstant " ، يمكننا الحصول على قيم جديدة قادمة من الكميات المادية. لاحظ أنه ، كما هو الحال في جميع لغات الكمبيوتر ، فإن الأعداد الصحيحة الصحيحة والأرقام المنطقية إما أعداد صحيحة صريحة أو أرقام عقلانية (ولكن ليست عشري).
يمكن أن ترتبط العديد من الثوابت الفيزيائية بالمعادلات التي تقدمها النظريات الفيزيائية لمختلف مجالات الفيزياء. في المستقبل ، نريد أن نقتصر على نظرية الظواهر الكهرومغناطيسية الأساسية ، والتي سيتم فيها تقليل خطأ الثوابت إلى خطأ ثابت البنية الدقيقة.
وريدبرج ثابت
. إذا أدرجنا ، على سبيل المثال ، ظواهر الجاذبية ، فسنضطر إلى استخدام ثابت الجاذبية G ، الذي يتم قياسه بشكل مستقل ، على الرغم من أنه يحتوي على خطأ كبير جدًا (وهذا هو السبب في أن NSF لديها ما يسمى "
Big-G Challenge ").
علاوة على ذلك ، فنحن نحصر أنفسنا بالكميات الكهربائية والمغناطيسية والكتلة التي يتم تقليل أخطاءها إلى وحدات
و
.
أدناه نستخدم الدالة
Around الجديدة للتعبير عن القيم مع الأخطاء المقابلة
و
.
حاليا ، وفقا ل CODATA 2014 ، الخطأ النسبي ل
هو على وشك
و من اجل
حول
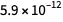
. كما ترون ، الخطأ ل
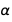
أكثر من ل
.
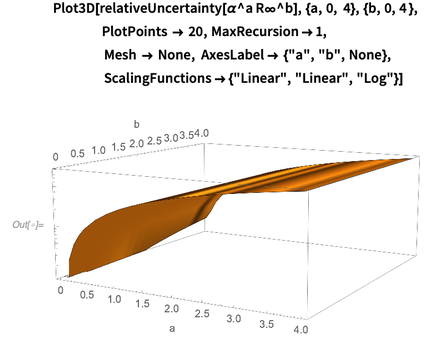
يوجد أدناه رسم بياني للخطأ النسبي log-base-10
كوظائف
أ و
ب . من الواضح ، بالنسبة للدرجات الصغيرة ، يعتمد الخطأ النسبي للمنتج بشكل ضعيف على الأسين
a و
b . يوضح هذا الرسم البياني أن اعتماد الخطأ
يسيطر نسبة إلى (الأس البنية الدقيقة). يتم تفسير هذه الملاحظة بحقيقة أن خطأ ثابت Rydberg أقل بمقدار 50 مرة من خطأ ثابت البنية الدقيقة.
لحساب أخطاء الثوابت المختلفة في SI الجديد ، سوف نستخدم الخطوات التالية:
• استرداد تمثيل مكافئ للثوابت المادية يمكن الوصول إليها من فئة كيان
PhysicalConstant .
هذه المساواة بين الثوابت الفيزيائية هي قوانين الفيزياء وعلى هذا النحو ينبغي الحفاظ عليها في كل من SI القديم والجديد.
• فكر في الصيغ كمجموعة من المعادلات الجبرية التي يمكن من خلالها تطبيق طرق استبعاد مختلفة للتعبير عن ثابت من خلال مزيج من سبعة ثوابت أساسية للـ SI الجديد ، وكذلك ثوابت البنية الدقيقة
ورايدبرج الثوابت
.
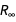
هذه هي الثوابت الأساسية التسعة التي نسمح بتطبيقها في تعريفات كل ثابت جديد تم دراسته. (من الناحية الفنية ، هناك 10 ثوابت في القائمة ، ولكن بسبب علاقة القياس البسيطة بين
h و
ℏ ، يوجد في الواقع تسعة ثوابت "مختلفة" في هذه القائمة.)
تحتوي فئة الكيان "
PhysicalConstant " على الكثير من المعلومات حول العلاقات بين الثوابت المادية. على سبيل المثال ، فيما يلي أشكال مكافئة لأربعة ثوابت يتم قياسها حاليًا وسيتم تحديدها قريبًا على أنها تحتوي على قيم دقيقة.
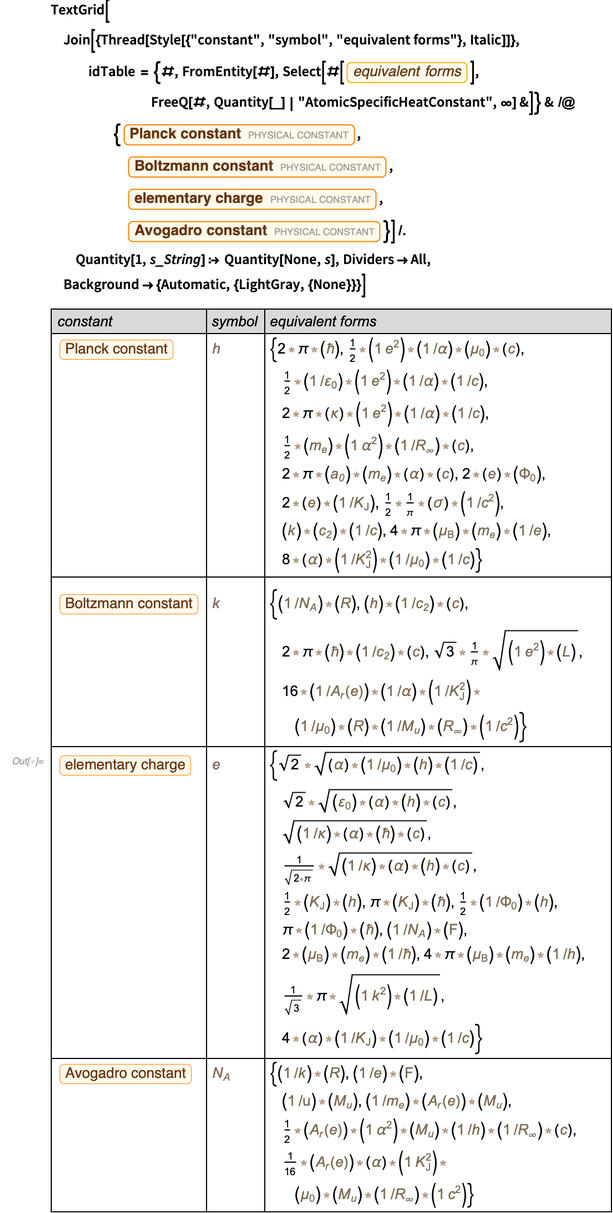
ضمن دقة القيم المقاسة ، تعمل كل عناصر الوحدة هذه الآن. إليك فحص رقمي سريع لأشكال بديلة لثابت بلانك. لكن القيمة العددية المحددة ، وخاصة الخطأ ، تعتمد على الشكل الفعلي للعرض التقديمي.
Around [], .
. .
, . , ? , , , , , .
, , ( ,
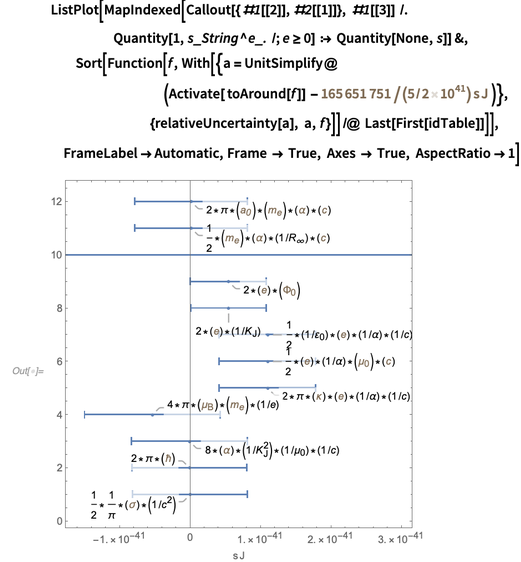
الكيان [" PhysicalConstant" ،. ] وبالكمية [ 1 ،. ] هي متساوية). السبب في أننا نستخدم الكيانات ، بدلاً من الكميات في الحسابات اللاحقة ، ذو شقين: أولاً ، الكيانات هي تمثيلات مريحة وسهلة القراءة ؛ وثانياً ، لا تخترق الدوال الجبرية (مثل GroebnerBasis ) الكميات لتحديد طبيعة الوسيطة الأولى.
ثم نجعل كل الهويات متعدد الحدود. الخطوة الأخيرة تعني: (1) طرح الجانب الأيسر من الجانب الأيمن ؛ و (2) أنه لم تعد هناك قوى كسرية (مثل الجذور التربيعية) للثوابت. نجري هذا التحويل إلى متعدد الحدود من خلال البحث عن جميع الأسس الكسرية وإيجاد LCM (أصغر عامل مشترك) لجميع قواسمها.
فيما يلي واحدة من المعادلات السابقة التي تحتوي على ثوابت بقوة كسرية.
بعد تعدد الحدود ، وصلنا إلى كثيرات الحدود للعديد من المتغيرات في الثوابت الثلاثة الموجودة. يجب القضاء على كثيرات الحدود.
يوضح الجدول التالي كيفية تطبيق الدالة
toPolynomial على النماذج المكافئة الموضحة مسبقًا مقابل شحنة أولية. بعد تقديس ℏ في
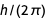
، بعض الحدود المتعددة الناتجة تصبح متطابقة.
الآن ، استنادًا إلى الثوابت المادية المتاحة (بدون الثوابت المستخدمة في تعريف SI الجديد) ، نحصل على أشكال مكافئة كافية لإنشاء مجموعة من المعادلات.
فيما يلي قائمة بالمعادلات متعددة الحدود التي تم الحصول عليها للتعبير عن شحنة أولية.
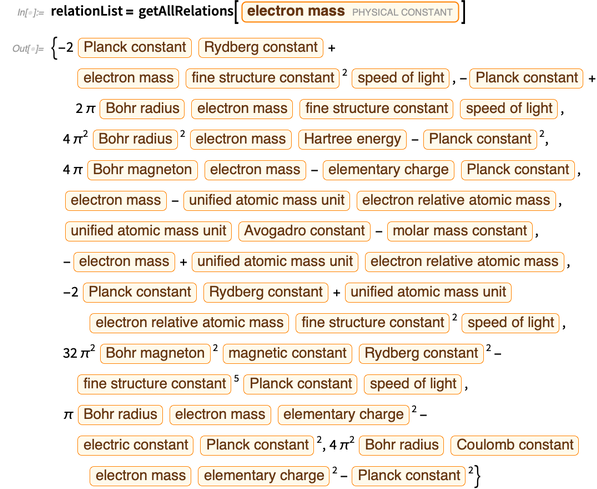
نعبر عن جميع الأخطاء من خلال الأخطاء
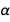
و
. فقط هذان الثوابتان يكفيان للتعبير عن خطأ العديد من الثوابت الفيزيائية. ونظرًا لأن أخطائهم مستقلة عن بعضها البعض ، وبما أن الأخطاء صغيرة جدًا ، فإن هذين الثوابت المعروفة جيدًا هما الأنسب للتعبير عن نسخة جديدة محسنة (بمعنى الأخطاء) من العديد من الثوابت الفيزيائية. وبالطبع ، نحن نسمح لجميع الثوابت الدقيقة السبعة من SI الجديد ؛ لأنها كميات دقيقة ، فإن وجودها لن يغير الخطأ.
العمل الرئيسي على التعبير عن ثابت معين من حيث ثوابت SI و
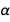
و
سيتم تنفيذها بواسطة وظيفة
GroebnerBasis . يعد تعيين
MonomialOrder -> ElventionOrder معلمة خطوة هامة تزيل جميع الكميات المادية "غير الضرورية" ، تاركة معادلة متعددة الحدود مع ثوابت محددة بدقة و (إذا لزم الأمر) بنية دقيقة وثوابت رايدبرج.
من خلال القضاء على الثوابت المرتبطة كتلة الإلكترون ، نحصل عليها
.
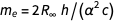
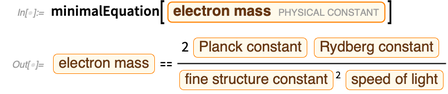
ينشأ خطأ هذا التعبير من المصطلح
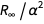
. يمكننا تحديد وظيفة تزيل العضو
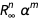
تسبب خطأ.
للحصول على تمثيل أكثر إحكاما ، يمكننا تحديد دالة تقوم بإرجاع نموذج مكافئ ، وكذلك أخطاء قديمة وجديدة - في شكل سلسلة.
ننهي المدونة من خلال تقديم جدول بالأخطاء القديمة والجديدة لأكثر من اثني عشر ثوابت مادية. يتم تحديد هذه القائمة كمثال تمثيلي ؛ يمكن معالجة الثوابت الأخرى بطريقة مماثلة (قد يتطلب ذلك إضافة ثوابت غير دقيقة إضافية للحفظ ، مثل ثابت الجاذبية أو معلمات النموذج القياسي).
الجمع بين الصفوف في جدول يعطي النتيجة التالية للتمثيل الأمثل لهذه الثوابت في نظام وحدة SI الجديد.
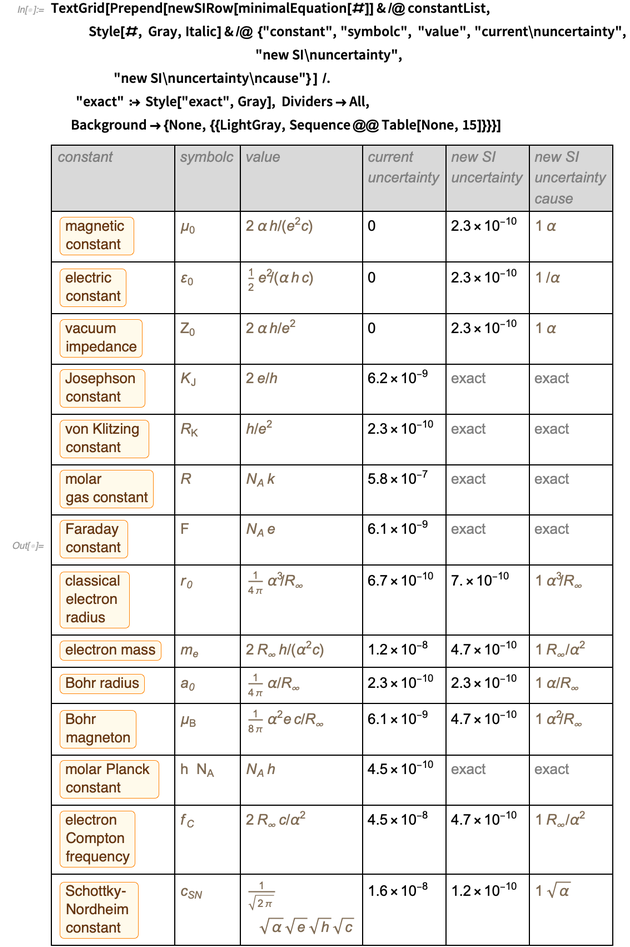
لقد كان جدول نعتزم عرضه ، وتمكنا من عرضه. انتبه إلى المظهر
في البسط والمقام
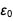
و
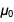
بحيث بعد الحد النتيجة
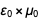
لقد أصبح
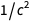
. يمكن العثور على قائمة مماثلة في أسفل صفحة ويكيبيديا حول
إعادة تعريف وحدات SI .
الآن يمكننا أن نتوقع بهدوء
2019 اليوم العالمي للمقاييس لعالم أفضل بشكل أساسي ، موصوف من خلال الثوابت الأساسية.
قم بتنزيل مدونة
دفتر Wolfram .
نظام مؤقت ولفرام الرياضياتلديك سؤال؟ معلومات الاتصال- russia@wolfram.com