مقدمة
النظر في تحويل المويجات المنفصلة (DWT) تنفيذها في مكتبة PyWavelets
PyWavelets 1.0.3 . PyWavelets هو برنامج مجاني مفتوح المصدر تم إصداره بموجب ترخيص MIT.
عند معالجة البيانات على جهاز كمبيوتر ، يمكن إجراء نسخة منقولة من تحويل المويجات المستمر ، والتي تم شرح أساسياتها في مقالتي السابقة. ومع ذلك ، فإن تحديد القيم المنفصلة للمعلمات (أ ، ب) للموجات التي لها خطوة تعسفية anda و Δb يتطلب عددًا كبيرًا من العمليات الحسابية.
بالإضافة إلى ذلك ، فإن النتيجة هي وجود عدد كبير من المعاملات ، وهو ما يتجاوز بكثير عدد عينات الإشارة الأصلية ، وهو أمر غير مطلوب لإعادة بنائها.
يوفر تحويل المويجات المنفصل (DWT) المنفَّذ في مكتبة PyWavelets معلومات كافية لتحليل الإشارة وتوليفها ، بينما تكون اقتصادية من حيث عدد العمليات والذاكرة المطلوبة.
متى يجب استخدام تحويل المويجات بدلاً من تحويل فورييه
سوف يعمل تحويل فورييه جيدًا عندما يكون طيف التردد ثابتًا. في هذه الحالة ، تكون الترددات الموجودة في الإشارة مستقلة عن الوقت ، وتحتوي الإشارة على ترددات xHz موجودة في أي مكان في الإشارة. غير مستقرة الإشارة ، وأسوأ النتائج. هذه مشكلة ، لأن معظم الإشارات التي نراها في الحياة الحقيقية غير مستقرة في الطبيعة.
تحويل فورييه لديه دقة عالية في مجال التردد ، ولكن دقة الصفر في المجال الزمني. نعرض هذا في المثالين التاليين.
إدراجimport numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt
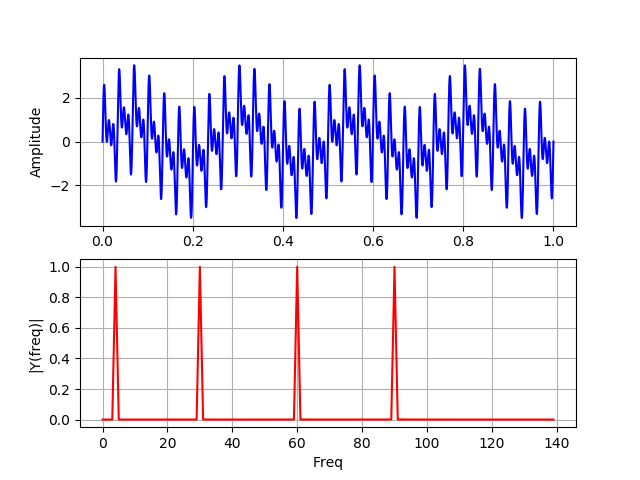
على هذا الرسم البياني ، توجد جميع الترددات الأربعة في الإشارة خلال كامل وقت تشغيلها.
إدراج import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt
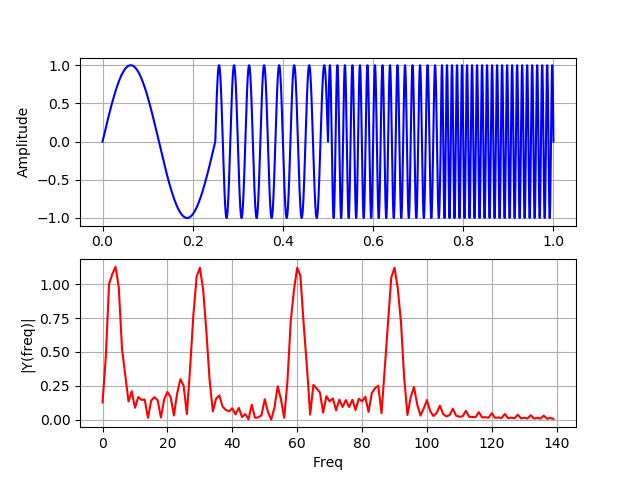
على هذا الرسم البياني ، لا تتداخل الإشارات مع الوقت ، فالفصوص الجانبية ناتجة عن فجوة بين أربعة ترددات مختلفة.
بالنسبة إلى أطياف التردد التي تحتوي على القمم الأربعة نفسها تمامًا ، لا يستطيع تحويل فورييه تحديد مكان وجود هذه الترددات في الإشارة. أفضل طريقة لتحليل الإشارات باستخدام طيف تردد ديناميكي هي تحويل المويجات.
الخصائص الرئيسية للموجات
يعتمد اختيار النوع ، وبالتالي خصائص المويجات ، على مهمة التحليل ، على سبيل المثال ، لتحديد القيم الفعالة للتيارات في صناعة الطاقة الكهربائية ، حيث توفر الأشكال الموجية ذات الترتيب العالي في Ingrid Daubechies دقة أكبر. يمكن الحصول على خصائص المويجات باستخدام دالة pywt.DiscreteContinuousWavelet () في القائمة التالية:
إدراج import pywt from pylab import * from numpy import * discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar'] print('discrete_wavelets-%s'%discrete_wavelets ) st='db20' wavelet = pywt.DiscreteContinuousWavelet(st) print(wavelet) i=1 phi, psi, x = wavelet.wavefun(level=i) subplot(2, 1, 1) title(" - -%s"%st) plot(x,psi,linewidth=2, label='level=%s'%i) grid() legend(loc='best') subplot(2, 1, 2) title(" - -%s"%st) plt.plot(x,phi,linewidth=2, label='level=%s'%i) legend(loc='best') grid() show()
نحصل على:
discrete_wavelets - ['db5' و 'sym5' و 'coif5' و 'haar']
Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False
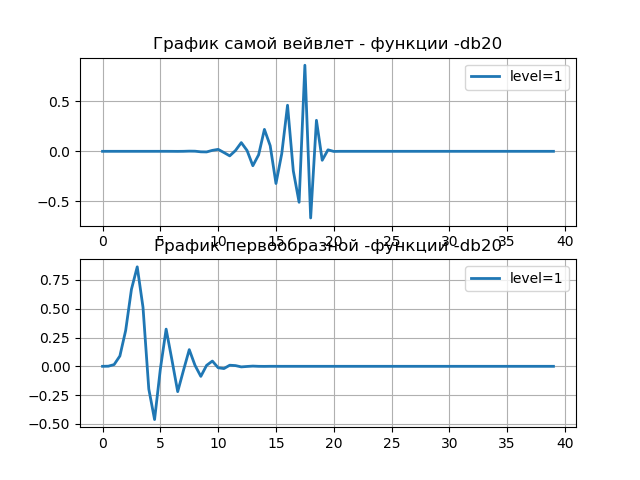
في عدد من الحالات العملية ، هناك حاجة للحصول على معلومات حول التردد المركزي للمويجة psi - وهي وظيفة يتم استخدامها ، على سبيل المثال ، في تحليل المويجات للإشارات لاكتشاف العيوب في التروس:
import pywt f=pywt.central_frequency('haar', precision=8 ) print(f)
0.9961089494163424 0.9961089494163424
باستخدام تردد المركز
يمكن للمويجات الأمومية وعامل القياس "أ" تحويل المقاييس إلى ترددات زائفة
باستخدام المعادلة:
أوضاع تمديد الإشارة
قبل حساب تحويل المويجات المنفصل باستخدام
مصارف التصفية ، يصبح من الضروري
إطالة الإشارة . اعتمادًا على طريقة الاستقراء ، قد تحدث بعض التحف الفنية الهامة عند حدود الإشارة ، مما يؤدي إلى عدم الدقة في تحويل DWT.
يوفر PyWavelets العديد من تقنيات استقراء الإشارة التي يمكن استخدامها لتقليل هذا التأثير السلبي. لشرح هذه الطرق ، استخدم القائمة التالية:
قائمة مظاهرة من طرق تمديد إشارة import numpy as np from matplotlib import pyplot as plt from pywt._doc_utils import boundary_mode_subplot

توضح الرسوم البيانية كيف تتوسع الإشارة القصيرة (الحمراء) (سوداء) إلى ما وراء طولها الأصلي.
تحويل المويجات المنفصلة
لإظهار DWT ، سوف نستخدم إشارة ذات طيف تردد ديناميكي ، والذي يزداد بمرور الوقت. تحتوي بداية الإشارة على قيم منخفضة التردد ، وتحتوي نهاية الإشارة على ترددات لمدى الموجة القصيرة. يتيح لنا ذلك تحديد أي جزء من طيف التردد يتم تصفيته بسهولة بمجرد النظر إلى محور الوقت:
إدراج from pylab import * from numpy import* x = linspace(0, 1, num=2048) chirp_signal = sin(250 * pi * x**2) fig, ax = subplots(figsize=(6,1)) ax.set_title(" ") ax.plot(chirp_signal) show()
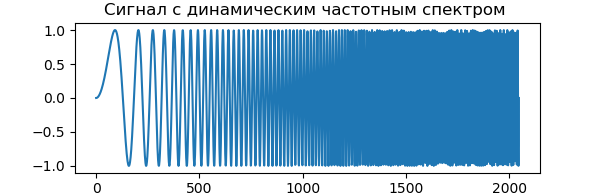
إن تحويل المويجات المنفصل في PyWavelets 1.0.3 هو دالة pywt.dwt () ، التي تحسب معاملات التقريب cA والمعاملات التفصيلية cD للتحويل المويضي المستوى الأول للإشارة المحددة بواسطة المتجه:
تحول المستوى الأول الإدراج import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-1') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-1') grid() legend(loc='best') show()
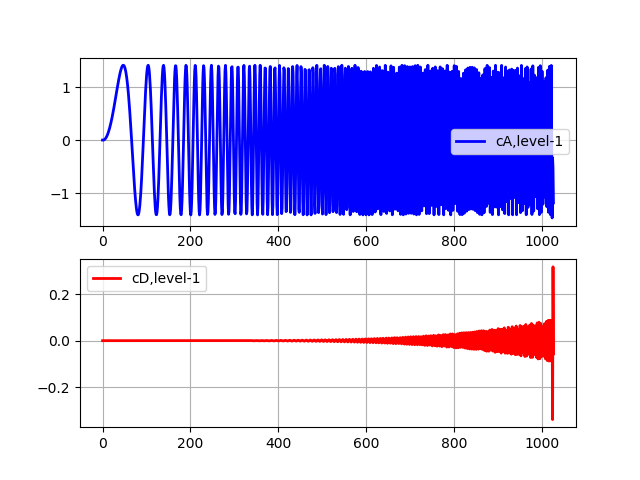
التحول المستوى 5 الإدراج import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()
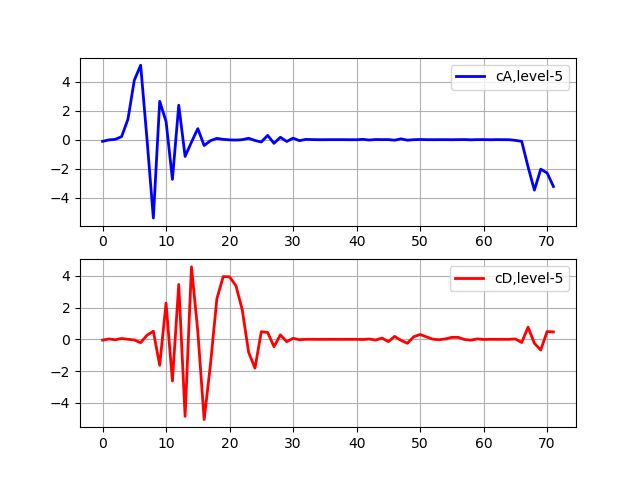
تمثل معاملات التقريب (cA) إخراج المرشح منخفض التمرير (مرشح المتوسط) DWT. تمثل معاملات التفاصيل (cD) مخرجات المرشح عالي التمرير (المرشح التفاضلي) DWT.
يمكنك استخدام دالة pywt.wavedec () لحساب معاملات المستوى الأعلى على الفور. تأخذ هذه الوظيفة إشارة الإدخال والمستوى كمدخل وتُرجع مجموعة واحدة من معاملات التقريب (المستوى n) ومجموعة n من معاملات التفاصيل (من المستوى 1 إلى المستوى n). فيما يلي مثال للمستوى الخامس:
from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()
نتيجة لذلك ، نحصل على نفس الرسوم البيانية كما في المثال السابق. يمكن الحصول على معاملات cA و cD بشكل منفصل:
ل cA:
import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1)
ل cD:
import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1)
تصفية البنك
تمت مناقشة بعض المشكلات المتعلقة بمستويات التحويل في القسم السابق. ومع ذلك ، يتم تطبيق DWT دائمًا كبنك مصفاة في شكل سلسلة من المرشحات عالية النجاح ومنخفضة المرور. البنوك المرشحة هي وسيلة فعالة للغاية لتقسيم الإشارة إلى نطاقات فرعية متعددة التردد.
في المرحلة الأولى على نطاق صغير ، وتحليل السلوك عالية التردد للإشارة. في المرحلة الثانية ، يزداد المقياس بعامل اثنين (يتناقص التردد بعامل اثنين) ، ونحلل سلوك حوالي نصف الحد الأقصى للتردد. في المرحلة الثالثة ، يكون عامل المقياس أربعة ، ونحلل سلوك التردد بحوالي ربع الحد الأقصى للتردد. وهذا يستمر حتى نصل إلى أقصى مستوى من التحلل.
يمكن حساب الحد الأقصى لمستوى التحلل باستخدام دالة pywt.wavedec () ، بينما سيبدو التحليل والتفاصيل كما يلي:
إدراج import pywt from pywt import wavedec from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data= sin (250 * pi * x**2) n_level=pywt.dwt_max_level(len(data), 'sym5') print(' : %s'%n_level) x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=7) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-7') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-7') grid() legend(loc='best') show()
نحصل على:
مستوى التحلل الأقصى: 7
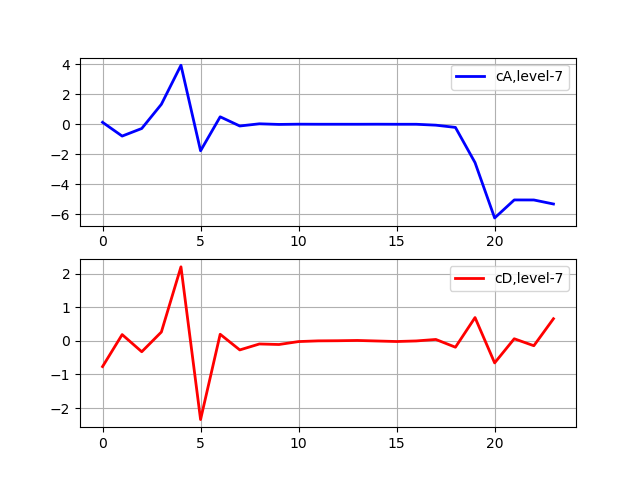
يتوقف التحلل عندما تصبح الإشارة أقصر من طول المرشح لموجة معينة من sym5. على سبيل المثال ، لنفترض أن لدينا إشارة بترددات تصل إلى 1000 هرتز. في المرحلة الأولى ، نفصل إشارة لدينا إلى أجزاء منخفضة التردد وعالية التردد ، أي 0-500 هرتز و 500-1000 هرتز. في المرحلة الثانية ، نأخذ الجزء ذو التردد المنخفض ونقسمه مرة أخرى إلى قسمين: 0-250 هرتز و 250-500 هرتز. في المرحلة الثالثة ، قسمنا الجزء 0-250 هرتز إلى الجزء 0-125 هرتز والجزء 125-250 هرتز. يستمر هذا حتى نصل إلى الحد الأقصى لمستوى التحلل.
تحليل ملفات wav باستخدام fft فورييه و scalograms المويجات
للتحليل ، استخدم
ملف WebSDR . النظر في تحليل إشارة مخفضة باستخدام triang من scipy.signal وتنفيذ تحويل فورييه منفصلة في بيثون (قدم من scipy.fftpack). إذا كان طول تسلسل fft لا يساوي 2n ، فبدلاً من تحويل فورييه السريع (fft) ، سيتم تنفيذ تحويل فورييه المنفصل (dft). هذه هي الطريقة التي يعمل بها هذا الفريق.
نستخدم المخزن المؤقت لتحويل فورييه السريع وفقًا للمخطط التالي (البيانات الرقمية على سبيل المثال):
fftbuffer = np.zeros (15) ؛ إنشاء مخزن مؤقت مليئة الأصفار.
fftbuffer [: 8] = x [7:] ؛ نقل نهاية الإشارة إلى الجزء الأول من المخزن المؤقت ؛ fftbuffer [8:] = x [: 7] —ننقل بداية الإشارة إلى الجزء الأخير من المخزن المؤقت ؛ X = fft (fftbuffer) - نحن نعتبر تحويل فورييه لمخزن مؤقت مليء بقيم الإشارة.
لجعل طيف المرحلة أكثر قابلية للقراءة ، يكون نشر الطور قابلاً للتطبيق. للقيام بذلك ، قم بتغيير الخط مع حساب خاصية المرحلة: pX = np.unwrap (np.angle (X)).
قائمة لتحليل جزء إشارة fft import numpy as np from pylab import * from scipy import * import scipy.io.wavfile as wavfile M=501 hM1=int(np.floor((1+M)/2)) hM2=int(np.floor(M/2)) (fs,x)=wavfile.read('WebSDR.wav') x1=x[5000:5000+M]*np.hamming(M) N=511 fftbuffer=np.zeros([N]) fftbuffer[:hM1]=x1[hM2:] fftbuffer[N-hM2:]=x1[:hM2] X=fft(fftbuffer) mX=abs(X) pX=np.angle(X) suptitle(" WebSDR") subplot(3, 1, 1) st=' (WebSDR.wav)' plot(x,linewidth=2, label=st) legend(loc='center') subplot(3, 1, 2) st=' ' plot(mX,linewidth=2, label=st) legend(loc='best') subplot(3, 1, 3) st=' ' pX=np.unwrap(np.angle(X)) plot(pX,linewidth=2, label=st) legend(loc='best') show()

للتحليل المقارن ، سوف نستخدم
scalogram المويجات التي يمكن بناؤها باستخدام شجرة = pywt.wavedec (إشارة ، 'coif5') وظيفة في matplotlib.
قائمة المويجات Scalograms from pylab import * import pywt import scipy.io.wavfile as wavfile
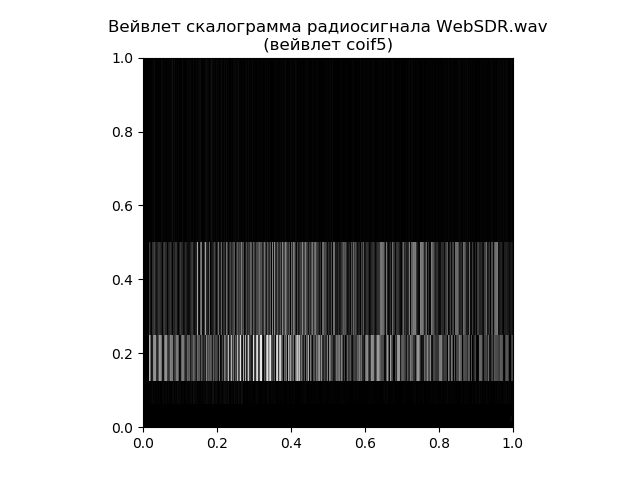
وبالتالي ، فإن scalogram يعطي إجابة أكثر تفصيلا لسؤال توزيع الترددات مع مرور الوقت ، وتحويل فورييه السريع هو المسؤول عن الترددات نفسها. كل هذا يتوقف على المهمة ، حتى لو كان هذا مثال بسيط.
النتائج
- ويرد الأساس المنطقي لاستخدام تحويل المويجات منفصلة للإشارات الديناميكية.
- يتم توفير أمثلة لتحليل المويجات باستخدام PyWavelets 1.0.3 ، وهو برنامج مجاني مفتوح المصدر تم إصداره بموجب ترخيص MIT.
- تعتبر أدوات البرمجيات للاستخدام العملي لمكتبة PyWavelets.