عند تحليل مشكلة أوليمبية واحدة ، سوف نمضي على طول الممرات المتعرجة لتوليد المتاهات ومرورها ، وسنرى أيضًا في لغة جوليا بساطة تنفيذ حدود الخوارزميات على الشفرة الزائفة الخاصة بها.

مهمة

المتاهة عبارة عن مربع متقلب من 10 إلى 10 ، وفي بعض الخلايا توجد عوائق ، وهناك مخرج في خلية واحدة. الروبوت في مثل هذه المتاهة ويمكنه تنفيذ 4 أوامر: تحريك خلية واحدة إلى أسفل أو أعلى أو اليمين أو اليسار. إذا حاول الروبوت تجاوز حدود المتاهة أو الذهاب إلى القفص بعائق ، فسيظل في مكانه. إذا دخل الروبوت إلى المخرج ، فإنه يخرج من المتاهة ويتجاهل الأوامر الأخرى. اكتب برنامجًا للروبوت ، ينفذ الروبوت الذي في أي حال يخرج منه ، بغض النظر عن الخلية التي كان موجودًا فيها في البداية. يجب أن يتكون البرنامج من أكثر من 1000 فريق.

تنسيق الإدخال

لا يوجد دخول. تحتاج إلى كتابة برنامج لشرط واحد محدد
المتاهة.
إصدار المتاهة التي يمكنك نسخها. 0 - خلية حرة ، 1 - عقبة ، x -
مخرج

0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000 

تنسيق الإخراج

سطر واحد يتكون من الأحرف U و D و R و L بطول لا يزيد عن 1000

تدريب

أولئك الذين لم يعملوا مع الرسومات في جوليا يحتاجون إلى تنزيل الحزم

 using Pkg Pkg.add("Plots") Pkg.add("Colors") Pkg.add("Images") Pkg.build("Images") #     

من الأنسب العمل في Jupyter ، حيث سيتم عرض الصور مباشرة أثناء العمل. هنا يمكنك العثور على التثبيت ، بالإضافة إلى مقدمة ومهام للمبتدئين.

في حالة مهمتنا هناك نسخة من المتاهة للنسخ

 S0 = "0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000" 

لرسم متاهة ، تحتاج إلى جعل مصفوفة. نظرًا لأننا لا نريد وضع مسافات يدويًا ، فسنعمل مع السطر:

 S1 = prod(s-> s*' ', '['*S0*']') # prod(fun, arr)    arr #     fun #  julia  *   "[ 0 0 1 1 0 1 0 0 1 1 \n 0 1 0 0 0 0 1 0 0 0 \n 0 1 1 0 x 0 0 0 0 0 \n 0 0 1 0 0 0 0 1 0 0 \n 0 0 0 0 1 1 1 0 0 0 \n 0 0 0 0 1 0 0 1 0 0 \n 0 0 0 0 0 1 0 0 1 0 \n 0 1 0 0 1 0 1 0 1 0 \n 0 0 1 1 0 0 1 0 1 0 \n 1 0 0 0 0 1 1 0 0 0 ] " 

استبدال الحرف المربك x برقم وتحليل السلسلة ، نحصل على مصفوفة عدد صحيح تحدد متاهاتنا. بعد ذلك ، من أجل راحة أكبر ، قم بتغييرها إلى أصفار ، والأصفار إلى أخرى ، وأرفق المتاهة بجدار:

 S2 = replace(S1, 'x'=>'9') M0 = S2 |> Meta.parse |> eval m,n = size(M0) M1 = replace(M0, 1=>0, 0=>1) M = zeros(Int64,m+2,n+2) for i in 2:m+1, j in 2:n+1 M[i,j] = M1[i-1,j-1] end M # Maze map matrix 12×12 Array{Int64,2}: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 

في المصفوفة

 length(M) 144 

الخلايا ومنهم

 sum(M)-9 70 

التي يمكنك المشي ، وهذا هو - مواقف الانطلاق المحتملة. يمكنك عرض النتيجة عن طريق إنشاء رسم بياني ثنائي الأبعاد

 using Plots heatmap(M, yaxis = :flip) # flip -   

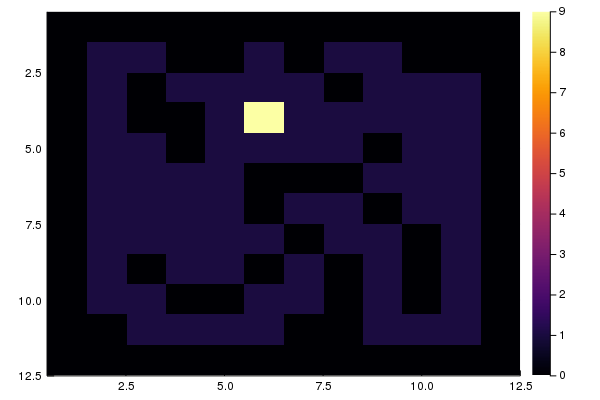
التحقق من الحل

بادئ ذي بدء ، تحتاج إلى وضع إجراءات تحقق من صحة الحل المقترح. اضبط النوع المركب Point لاستخدام مصطلحات النقاط والإحداثيات:

 mutable struct Point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end 

والآن تحتاج إلى معرفة كيفية ترجمة سلسلة من الأوامر المفهومة للروبوت إلى كود.

الفكرة بسيطة للغاية: هناك إحداثي بدء ، خط يأتي بخوارزمية توضح كيفية المشي. نأخذ حرفًا واحدًا وننظر إلى أي من الخلايا المجاورة للخطوة. إلى الإحداثيات الحالية نضيف القيمة المخزنة في هذه الخلية. أي إذا كان هناك صفر (جدار) ، فإننا لم نتحرك في أي مكان ، وإلا فقد اتخذنا خطوة صغيرة في الاتجاه المطلوب.

باستخدام قوة metaprogramming ، يمكنك استبدال تسلسل الاتجاهات الواردة برمز ضخم وموحد وتنفيذها

 S = "RRLDUURULDDRDDRRRUUU" S1 = replace(S , "R"=>"c.y+=M[cx, c.y+1];") S1 = replace(S1, "L"=>"cy-=M[cx, cy-1];") S1 = replace(S1, "U"=>"c.x+=M[c.x+1, cy];") S1 = replace(S1, "D"=>"cx-=M[cx-1, cy];") #  - start point Sp = eval( Meta.parse(S1) ) 

لكن هذه الطريقة بها عدد من الإزعاج ، لذلك ، سوف نستخدم العوامل الشرطية الكلاسيكية. بالمناسبة ، فإن الإشارة إلى المخرج بالرقم 9 هي خدعة صغيرة: من أجل عدم التحقق من كل خلية ، وما إذا كان هو المخرج ، نبدأ الحركة بإضافة القيمة المخزنة في خلية معينة. عندما ينتقل الروبوت إلى المخرج ، تتم إضافة عدد كبير عن عمد إلى إحداثيته ، بحيث ينتقل الروبوت إلى ما وراء حدود المصفوفة ، والتي يمكن اكتشافها كخطأ باستخدام الكتلة:

 try #     catch #       end 

وبالتالي ، فإننا نقوم بتنفيذ وظيفة تتحقق مما إذا كان الروبوت يصل إلى المخرج بدءًا من النقطة c تنفيذ الأوامر من السلسلة str :

 function isexit(str, c) scatter!([cy],[cx]) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end 

دعنا نجمع وظيفة ستعمل على تكرار جميع المواقف المبدئية

 function test(Str) k = 0 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

تحقق من الأوامر:

 S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU" heatmap(M, yaxis = :flip) test(S) # 10 test completed from 70 plot!(legend = false) 

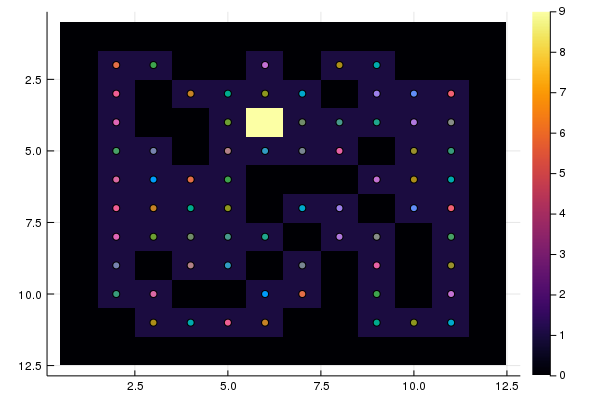
تم اختبار جميع نقاط البداية ، وأدت فقط 10 إلى الخروج. من الضروري بناء طرق من كل نقطة إلى الخروج.

قبل الغطس في جيل ومراحل المتاهات ، سنوفر نتائجنا. سنستخدم حزمة Images.jl التي توفر العديد من الاحتمالات في مجال معالجة الصور ( مثال جيد ). واحدة من أدواته الداعمة هي حزمة Colors.jl ، التي توسع قدرة جوليا على العمل مع الألوان.

 using Images clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x) maze = clrs.(M) # maze = Gray.(maze) # save("D:/dat/maze12x12.png", maze) 

البحث العمق

نفذت الفكرة من مقال عن هبر .
الفكرة بسيطة: إنشاء شبكة من الجدران

 M = 10 N = 10 A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1 Gray.(A) # from Images.jl 

ثم ، من خلال حلقات ، ونحن اختراق الطريق والفروع. نحدد دالة تعثر على المناطق غير المرخصة المجاورة (سنقوم بتعيينها ، على سبيل المثال ، بواسطة الشيطان) وإرجاع واحد من هذه الجيران (إذا لم يكن هناك جيران غير مرغوب فيهم ، فستُرجع نقطة العلم):

 function neighbours2(A,p, n, m) nbrs = [Point(px, p.y+2), # up Point(px, py-2), # down Point(px-2, py), # left Point(p.x+2, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==2 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(-1,-1) end 

سوف نكسر الجدران مثل هذا:

 function breakwall(A, newp,oldp) #  : x = (newp.x + oldp.x) >> 1 #   y = (newp.y + oldp.y) >> 1 A[x,y] = 1 end 

خوارزمية

1. جعل الخلية الأولية الحالية ووضع علامة عليه كما زار.
2. بينما هناك خلايا غير مرخصة
   1. إذا كانت الخلية الحالية "جيران" غير مرغوب فيهم
   1. ادفع الخلية الحالية إلى المكدس
   2. حدد خلية عشوائية من المجاورة
   3. إزالة الجدار بين الخلية الحالية والخيار المحدد
   4. جعل الخلية المحددة الحالية ووضع علامة عليه كما زار.
   2. خلاف ذلك ، إذا كان المكدس غير فارغ
   1. اسحب القفص من المكدس
   2. جعله الحالي
   3. خلاف ذلك
   1. حدد خلية عشوائية غير مرخصة ، وجعلها الحالية ووضع علامة عليها كما زار.

 function amazeng(n, m) M = [ 2(i&j&1) for i in 0:n, j in 0:m ]; p = Point(2,2) #   lifo = [] #   push!(lifo, p) #i = 0 while length(lifo) != 0 #     M[px,py] = 1 #     np = neighbours2(M, p, n, m) # new point #    -   if np.x == np.y == -1 p = pop!(lifo) else push!(lifo, p) breakwall(M, np, p) p = np #i+=1 #maze = Gray.(M/2) #save("D:/dat/maze$i.png", maze) end end M[1,2] = 1 #  M[n,m+1] = 1 #  Gray.(M) end 

 lbrnt = amazeng(36, 48) # save("D:/dat/maze111.png", lbrnt) 

خوارزمية البحث عن مسار التراجع:

1. جعل الخلية الأولية الحالية ووضع علامة عليه كما زار.
2. حتى يتم العثور على حل
   1. إذا كانت الخلية الحالية "جيران" غير مرغوب فيهم
   1. ادفع الخلية الحالية إلى المكدس
   2. حدد خلية عشوائية من المجاورة
   3. جعل الخلية المحددة الحالية ووضع علامة عليه كما زار.
   2. خلاف ذلك ، إذا كان المكدس غير فارغ
   1. اسحب القفص من المكدس
   2. جعله الحالي
   3. خلاف ذلك ، لا توجد وسيلة للخروج.

نحن نبحث عن الجيران على عكس ذلك وداخل دائرة نصف قطرها خلية واحدة ، وليس من خلال واحدة:

 function neighbours1(A, p, n, m) nbrs = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==1 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(0,0) end 

تحديد خوارزمية لتمرير المتاهة مع رسم الطريق ومحاولات غير ناجحة

 function amazeng(img, start, exit) M = Float64.(channelview(img)) n, m = size(M) p = start M[exit.x,exit.y] = 1 lifo = [] push!(lifo, p) while px != exit.x || py != exit.y M[px,py] = 0.4 np = neighbours1(M, p, n, m) if np.x == np.y == 0 M[px,py] = 0.75 p = pop!(lifo) #  -  ,    #      else push!(lifo, p) p = np end end Gray.(M) end 

كما لاحظ البعض ، تسمى الوظيفة أيضًا ، مثل تلك التي تنشئها الخوارزميات (جدولة متعددة). عندما تسميها برقمين ، ستعمل على تحديد طريقة إنشاء المتاهة ، ولكن إذا قمت بالاتصال بها عن طريق تحديد الصورة ونقطتين (إحداثيات المدخلات والمخرجات) كحجة ، ثم في الإخراج نحصل على صورة مع تمرير المتاهة

 img0 = load("D:/dat/maze111.png") amazeng(img0) 

لنجرب متاهاتنا:

 img0 = load("D:/dat/maze12x12.png") n, m = size(img0) amazeng(img0, Point(11,9), Point(4,6) ) 

حتى إذا قمت بتعديل الوظيفة بحيث يتم تذكر المسار ، فإن الخوارزمية لا تزال غير فعالة بسبب المساحات المفتوحة. لكن متاهات يخرج كبيرة.

خوارزمية عشوائية بريم

بمجرد أن تبدأ في رسم المتاهات ، فلن تتوقف. لنقم بإجراء خوارزمية أخرى مثيرة للاهتمام:

• ابدأ بشبكة مليئة بالجدران.
• حدد خلية ، ووضع علامة عليها كجزء من المتاهة. إضافة جدران الخلايا إلى قائمة الجدار.
• في حين أن هناك جدران في القائمة:
  
  • حدد جدار عشوائي من القائمة. إذا تمت زيارة واحدة فقط من الخليتين التي يشاركها الجدار ، عندئذٍ:
    
    • اجعل الجدار ممرا ووضع علامة على الخلية غير المرئية كجزء من المتاهة.
    • إضافة جدران الخلايا المجاورة إلى قائمة الجدار.
  • أزل الجدار من القائمة.

 neighbors(p::Point) = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right function newalls!(walls, p, maze, n, m) nbrs = neighbors(p) for a in nbrs if 1<ax<n-1 && 1<ay<m-1 && !maze[ax,ay] push!(walls, a) #       . end end end function breakwall!(p, maze, n, m) nbrs = neighbors(p) #       if sum( a-> maze[ax,ay], nbrs) == 1 for a in nbrs if maze[ax,ay] # true =  px == ax ? nx = px : px>ax ? nx = p.x+1 : nx = px-1 py == ay ? ny = py : py>ay ? ny = p.y+1 : ny = py-1 maze[px,py] = true #   maze[nx,ny] = true px = nx py = ny return true end end else return false end end function prim(n, m) M = falses(n,m); #    p = Point(2, 2) M[px,py] = true walls = [] newalls!(walls, p, M, n, m) while length(walls) != 0 p = splice!( walls, rand(1:length(walls)) ) if breakwall!(p, M, n, m) newalls!(walls, p, M, n, m) end end M end 

 primaze = prim(19,19); Gray.(primaze) 

اتضح أكثر براعة وليس أقل رهيبة ، وخاصة عملية التجميع.

والآن ننفذ الخوارزمية الأكثر شيوعًا للعثور على أقصر الطرق:

الطريقة أ *

• يتم إنشاء 2 قوائم قمة - في انتظار واستعراضها بالفعل. تتم إضافة نقطة البداية إلى النقاط المعلقة ، وقائمة المراجعة التي تمت مراجعتها فارغة حتى الآن.
• لكل نقطة تحسب $$$H$ - المسافة التقريبية من النقطة إلى الهدف.
• من قائمة النقاط المراد النظر فيها ، النقطة مع أصغرها $$$H$ . دعها $$$X$ .
• إذا $$$X$ - الهدف ، ثم وجدنا الطريق.
• نحمل $$$X$ من القائمة المعلقة إلى قائمة المراجعة بالفعل.
• لكل نقطة من النقاط المجاورة ل $$$X$ (تشير إلى هذه النقطة المجاورة $$$Y$ ) ، قم بما يلي:
  
  • إذا $$$Y$ بالفعل في المراجعة - تخطي ذلك.
  • إذا $$$Y$ ليس بعد في قائمة الانتظار - إضافته هناك.
• إذا كانت قائمة النقاط المراد دراستها فارغة ، لكننا لم نصل إلى الهدف ، فهذا يعني أن المسار غير موجود.

للبدء ، دعنا نعرّف "نقطة" الفصل التي ستعرف مدى بعدها عن الهدف:

 mutable struct Point_h x::Int64 # horisont y::Int64 # vertical h::Float64 Point_h(x, y) = new(x, y, 0.) end 

الآن نحدد عملية المقارنة للهيكل ، طريقة لتأسيس وجود عنصر في صفيف ، وكذلك وظيفة إزالة عنصر ، إيجاد المسافة بين النقاط وإدراج الجيران:

 import Base: in, == ==(a::Point_h, b::Point_h) = ax==bx && ay==by function in(p::Point_h, Arr::Array{Point_h,1}) for a in Arr if a == p return true end end return false end function splicemin!(Arr)#::Array{Point_h,1} i = argmin( [ah for a in Arr] ) splice!(Arr, i) end dista(u,v) = hypot(vx-ux, vy-uy) # <=> sqrt( (vx-ux)^2 + (vy-uy)^2 ) neighbors(p::Point_h) = [Point_h(px, p.y+1), # up Point_h(px, py-1), # down Point_h(px-1, py), # left Point_h(p.x+1, py)] # right 

كما هو الحال دائما ، يمكن توضيح مشغلي غامضة باستخدام الأمر ? على سبيل المثال ?argmin ?splice ?argmin

وفي الواقع ، فإن الطريقة أ * نفسها

 function astar(M, start, final) #   -       isgood(p) = 1<px<n && 1<py<m && M[px,py] != 0 n, m = size(M) #       start.h = dista(start,final) closed = [] opened = [] push!(opened, start) while length(opened) != 0 X = splicemin!(opened) if X in closed continue end if X == final break end push!(closed, X) nbrs = neighbors(X) ygrex = filter(isgood, nbrs) for Y in ygrex if Y in closed continue else Yh = dista(Y, final) push!(opened, Y) end end end #    closed # return end 

نقوم بتحميل الصورة مع المتاهة وتقديمها في شكل مصفوفة:

 img0 = load("D:/dat/maze0.png") mazematrix = Float64.(channelview(img0)) 

ونحن نبني طريقًا للخروج من نقطة تعسفية:

 s = Point_h(11,9) # start f = Point_h(4,6) # finish M = copy(mazematrix) route = astar(M, s, f) i = 1 for c in route #   M[cx,cy] = 0.7 #save("D:/dat/Astar$i.png", M) i+=1 end Gray.(M) 

البحث من جميع المواقف يشبه هذا:

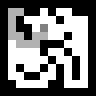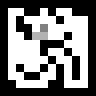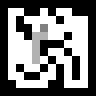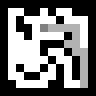
يرى أن الوكيل PRET يميل دائمًا إلى جانب المخرج وغالبًا ما يتحول إلى طريق مسدود ، مما يؤدي إلى خطوات غير ضرورية ، ويتم تذكر المسار بالكامل. يتم تجنب ذلك عن طريق إصدار أكثر تعقيدًا قليلاً من خوارزمية A *.

• يتم إنشاء 2 قوائم قمة - في انتظار واستعراضها بالفعل. تتم إضافة نقطة البداية إلى النقاط المعلقة ، وقائمة المراجعة التي تمت مراجعتها فارغة حتى الآن.
• لكل نقطة تحسب $$$F = G + H$ . $$$G$ - المسافة من البداية إلى النقطة ، $$$H$ - المسافة التقريبية من النقطة إلى الهدف. تخزن كل نقطة أيضًا رابطًا للنقطة التي جاءت منها.
• من قائمة النقاط المراد النظر فيها ، النقطة مع أصغرها $$$F$ . دعها $$$X$ .
• إذا $$$X$ - الهدف ، ثم وجدنا الطريق.
• نحمل $$$X$ من القائمة المعلقة إلى قائمة المراجعة بالفعل.
• لكل نقطة من النقاط المجاورة ل $$$X$ (تشير إلى هذه النقطة المجاورة $$$Y$ ) ، قم بما يلي:
  
  • إذا $$$Y$ بالفعل في المراجعة - تخطي ذلك.
  • إذا $$$Y$ ليس بعد في قائمة الانتظار - قم بإضافته إلى هناك ، مع تذكر الرابط $$$X$ وبعد حسابها $$$Y.G$ (هذا هو $$$X.G$ + المسافة من $$$X$ إلى $$$Y$ ) و $$$Y.H$ .
  • ولكن، إذا $$$Y$ في قائمة للنظر فيها - تحقق مما إذا $$$X.G$ + المسافة من $$$X$ إلى $$$Y$$$$<Y.G$ لذلك وصلنا إلى هذه النقطة $$$Y$ طريقة أقصر ، استبدال $$$Y.G$ في $$$X.G$ + المسافة من $$$X$ إلى $$$Y$ ، والنقطة التي أتوا منها $$$Y$ في $$$X$ .
• إذا كانت قائمة النقاط المراد دراستها فارغة ، لكننا لم نصل إلى الهدف ، فهذا يعني أن المسار غير موجود.

ولكن حتى مع الخطوات غير الضرورية ، فإن خيارنا يقع ضمن قيود المهمة ، لذا فإن تعديل البرامج سيكون واجبك.

حتى نهاية الأولمبياد ، لم يتبق شيء ، لكن ما زلنا بحاجة لمعرفة كيفية ترجمة نتائج خوارزمياتنا إلى أوامر من النموذج "RRLUUDL..."

وبعد كل هذه الأمور من خلال متاهات ، يمكننا أن نفترض أن الحل أبسط بكثير. في الواقع ، هناك خيار بسيط يطرح على الفور ، ولكني أردت حقًا صنع أشياء جميلة .

إذا وضعنا فناننا في منطقة مفتوحة وشرعنا في السير بشكل عشوائي ، فسوف يتردد بالقرب من مركز البداية. ولكن مع إدخال الجدران ، ستبدأ بعض الاتجاهات في التلاشي ، وستصبح درجات الحرية أقل ، وبنفس بيانات الإدخال ، يتحرك العامل مسافة أكبر.

في ما يلي نسختنا من فحص الفرق للتأكد من ملاءمتها لإنقاذ روبوت من متاهة:

 M = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0] mutable struct Point # point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end function isexit(str, c) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end function test(Str) k = 0 n, m = 10,10 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

الآن يكفي إنشاء خطوط عشوائية حتى تحصل على خطوط مناسبة لجميع المواضع التي تبدأ:

 using Random S = randstring("RLUD",200) "RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD" test(S) 41 test completed from 70 

بالإضافة إلى ذلك ، كان من الممكن عدم عناء الاختبار. كان يكفي لقراءة المهمة وإنشاء سلسلة عشوائية بأقصى شرط مسموح به:

 for i in 1:20 S = randstring("RLUD",1000) test(S) end 70 test completed from 70 70 test completed from 70 70 test completed from 70 70 test completed from 70 55 test completed from 70# 65 test completed from 70# 70 test completed from 70 70 test completed from 70 38 test completed from 70# 70 test completed from 70 70 test completed from 70 56 test completed from 70# 70 test completed from 70 70 test completed from 70 70 test completed from 70 16 test completed from 70# 70 test completed from 70 24 test completed from 70# 70 test completed from 70 70 test completed from 70 

وهذا هو ، مع احتمال 70 ٪ ، فإن الخط اجتياز الاختبارات.

هذا كل شيء. أتمنى للقارئ نجاحًا عشوائيًا والصبر والحدس لحلول واضحة.

للفضوليين - روابط لتعميق الموضوع:

• الرحلة الأكثر اكتمالا في جيل المتاهة
• النسخة الروسية
• طرق تايمز
• طريقتين
• خوارزمية إلر
• مولد على الانترنت
• طرق لإيجاد المسار بين النقاط على الإنترنت
• خوارزمية مسار نقطة البحث السريع
• A * على ويكيبيديا
• مقدمة إلى A *
• مقدمة إلى الخوارزمية A *
• شرح خوارزميات العثور على المسار
• مصدر الفن