هذا التعليق كان مدعوما بكتابة المقال. بتعبير أدق ، عبارة واحدة منه.

... إنفاق دورات الذاكرة أو المعالجات على العناصر بمليارات الدولارات ليس بالأمر الجيد ...

لقد حدث أن اضطررت إلى فعل ذلك مؤخرًا. وعلى الرغم من أن الحالة التي سأبحثها في المقال هي حالة خاصة - فالاستنتاجات والحلول المطبقة يمكن أن تكون مفيدة لشخص ما.

قليلا من السياق

يتعامل تطبيق iFunny مع كمية هائلة من محتوى الرسوم والفيديو ، ويعتبر البحث الغامض عن التكرارات أحد المهام المهمة للغاية. هذا بحد ذاته موضوع كبير يستحق مقالاً منفصلاً ، لكن اليوم سأتحدث قليلاً عن بعض الأساليب لحساب صفيفات كبيرة جدًا من الأرقام فيما يتعلق بهذا البحث. بالطبع ، لدى الجميع فهم مختلف عن "المصفوفات الكبيرة جدًا" ، وسيكون من الغباء التنافس مع مصادم هادرون ، لكن لا يزال. :)

إذا كانت الخوارزمية مختصرة جدًا ، فسيتم إنشاء توقيع رقمي (توقيع) لكل صورة من 968 عددًا صحيحًا ، وتتم المقارنة من خلال إيجاد "المسافة" بين التوقيعين. وبالنظر إلى أن حجم المحتوى في الشهرين الأخيرين وحدهما بلغ حوالي 10 ملايين صورة ، فإن القارئ اليقظ سوف يكتشفها بسهولة في أذهانه - هذه بالضبط هي "العناصر في مليارات المجلدات". من يهتم - مرحبا بكم في القط.

في البداية ، ستكون هناك قصة مملة حول توفير الوقت والذاكرة ، وفي النهاية ستكون هناك قصة قصيرة مفيدة حول حقيقة أنه في بعض الأحيان يكون من المفيد للغاية النظر إلى المصدر. ترتبط الصورة التي تجذب الانتباه مباشرة بهذه القصة المفيدة.

يجب أن أعترف أنني كنت أبكي قليلاً. في تحليل أولي للخوارزمية ، كان من الممكن تقليل عدد القيم في كل توقيع من 968 إلى 420. إنه بالفعل جيد مرتين ، لكن ترتيب الحجم يظل كما هو.

على الرغم من أنك إذا فكرت في الأمر ، فلم أكن أخدعه كثيرًا ، وسيكون هذا هو الاستنتاج الأول: قبل البدء في المهمة ، يجدر التفكير في الأمر - هل من الممكن تبسيطها بطريقة أو بأخرى مقدمًا؟

إن خوارزمية المقارنة بسيطة للغاية: يتم حساب جذر مجموع مربعات الاختلافات في التوقيعين ، مقسومًا على مجموع القيم المحسوبة مسبقًا (أي في كل تكرار سيبقى التجميع ولا يمكن إخراجه ليكون ثابتًا على الإطلاق) ومقارنته بالقيمة العتبة. تجدر الإشارة إلى أن عناصر التوقيع تقتصر على القيم من -2 إلى +2 ، وبالتالي ، فإن القيمة المطلقة للفرق تقتصر على القيم من 0 إلى 4.


لا شيء معقد ، ولكن الكمية تقرر.

النهج الأول ، ساذجة

//  const val d = 0.3 // 10.000.000 . //      , //        val collection: MutableList<Signature> = mutableListOf() // signature —   420   Byte class Signature(val signature: Array<Byte>, val norma: Double) fun getSimilar(signature: Signature) = collection .filter { calculateDistance(it, signature) < d } fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> Math.pow((value - second.signature[index]).toDouble(), 2.0) }.sum()) / (first.norma + second.norma) 

دعنا نحسب ما لدينا هنا بعدد العمليات:

10M Math.sqrt مربع جذور Math.sqrt
10M الإضافات والانقسامات / (first.norma + second.norma)
طرح وطرح 4.200M Math.pow((value - second.signature[index]).toDouble(), 2.0)
4.200M الإضافات 4.200M .sum()

ما هي الخيارات المتاحة لدينا:

1. مع مثل هذه الكميات ، إنفاق Byte كامل (أو ، لا سمح الله ، كان شخص ما قد خمن استخدام Int ) لتخزين ثلاثة أجزاء كبيرة هو مضيعة لا تُنسى.
2. ربما ، كيف تقلل من كمية الرياضيات؟
3. ولكن هل من الممكن القيام ببعض التصفية الأولية ، وهي ليست مكلفة من الناحية الحسابية؟

النهج الثاني ، نحن حزمة

بالمناسبة ، إذا اقترح شخص ما كيف يمكنك تبسيط العمليات الحسابية باستخدام هذه العبوة ، فستتلقى شكرًا كبيرًا بالإضافة إلى الكرمة. على الرغم من واحد ، ولكن من كل قلبي :)

One Long هي 64 بت ، والتي ، في حالتنا ، ستسمح لنا بتخزين 21 قيمة فيه (وسيبقى 1 بت بدون تسوية).

 //   20   Long class Signature(val signature: Array<Long>, val norma: Double) fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> calculatePartial(value, second.signature[index]) }.sum()) / (first.norma + second.norma) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L (0..60 step 3).onEach { val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7) sum += current * current } return sum.toDouble() } 

إنه أفضل من الذاكرة ( 4.200M مقابل 1.600M بايت ، إذا كان تقريبًا) ، ولكن ماذا عن الحسابات؟

أعتقد أنه من الواضح أن عدد العمليات قد بقي كما هو و 8.400M التحولات و 8.400M المنطقي 8.400M إضافتهم. ربما يمكن تحسينه ، ولكن الاتجاه لا يزال غير سعيد - هذا ليس ما أردنا.

النهج الثالث ، إعادة حزمة مع الغواصات الفرعية

في الصباح أستطيع أن أشم رائحة ، هنا يمكنك استخدام السحر قليلا!

لنقم بتخزين القيم ليس في ثلاث ، ولكن بأربع بتات. بهذه الطريقة:

نعم ، سنفقد كثافة التعبئة مقارنة بالإصدار السابق ، ولكن سنحصل على فرصة لاستلام Long مع 16 (وليس تمامًا) من الاختلافات مع أوم واحد من XOR مرة واحدة. بالإضافة إلى ذلك ، لن يكون هناك سوى 11 خيارًا لتوزيع البتات في كل nibble النهائية ، مما سيتيح لك استخدام القيم المحسوبة مسبقًا لمربعات الاختلافات.

 //   27   Long class Signature(val signature: Array<Long>, val norma: Double) // -1    val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L val difference = first xor second (0..60 step 4).onEach { sum += precomputed[(difference.ushr(it) and 0xF).toInt()] } return sum.toDouble() } 

من الذاكرة أصبح 2.160M مقابل 1.600M - غير سارة ، ولكن لا يزال أفضل من 4.200M الأولي.

دعنا نحسب العمليات:

10M ، جذور مربعة ، إضافات وأقسام
270M XOR
4.320 الإضافات ، التحولات ، 4.320 المنطقية ، ومقتطفات من الصفيف.

يبدو بالفعل أكثر إثارة للاهتمام ، ولكن ، على أي حال ، هناك الكثير من العمليات الحسابية. لسوء الحظ ، يبدو أننا قد أنفقنا بالفعل 20٪ من الجهود المبذولة لإعطاء 80٪ من النتيجة وحان الوقت للتفكير في أي مكان آخر يمكنك الربح. أول ما يتبادر إلى الذهن هو عدم الوصول إلى حساب على الإطلاق ، مع تصفية التواقيع غير المناسبة بشكل واضح مع بعض المرشحات الخفيفة.

النهج الرابع ، غربال كبير

إذا قمت بتحويل صيغة الحساب قليلاً ، فيمكنك الحصول على عدم المساواة هذا (كلما كانت المسافة المحسوبة أصغر ، كلما كان ذلك أفضل):


أي نحتاج الآن إلى معرفة كيفية حساب الحد الأدنى للقيمة الممكنة للجانب الأيسر من عدم المساواة استنادًا إلى المعلومات المتوفرة لدينا حول عدد البتات المحددة في Long . ثم ببساطة تجاهل كل التواقيع التي لا ترضيه.
واسمحوا لي أن أذكرك بأن x _يمكنني أخذ القيم من 0 إلى 4 (الإشارة ليست مهمة ، وأعتقد أنه من الواضح سبب ذلك). بالنظر إلى تربيع كل مصطلح ، فمن السهل اشتقاق نمط عام:


تبدو الصيغة النهائية هكذا (نحن لسنا في حاجة إليها ، لكنني استخلصتها لفترة طويلة وسيكون من العار أن ننسى وألا نظهر لأي شخص):


حيث B هو عدد البتات المحددة.

في الواقع ، في 64 بت واحد فقط من Long ، اقرأ 64 من النتائج المحتملة. ويتم احتسابها بشكل مسبق مقدمًا وإضافتها إلى مجموعة ، عن طريق القياس مع القسم السابق.

بالإضافة إلى ذلك ، من الاختياري تمامًا حساب كل الـ27 الطويلة - وهو ما يكفي لتجاوز العتبة في المرحلة التالية ويمكنك مقاطعة الشيك والإرجاع خطأ. الطريقة نفسها ، بالمناسبة ، يمكن استخدامها في الحساب الرئيسي.

 fun getSimilar(signature: Signature) = collection .asSequence() //     !? .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256) fun estimate(first: Signature, second: Signature):Boolean{ var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong() first.signature.forEachIndexed { index, value -> bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])] if (bitThreshold <= 0) return false } return true } 

هنا يجب أن يكون مفهوما أن فعالية هذا الفلتر (حتى السلبي) تعتمد بشكل كارثي على العتبة المحددة ، وعلى قوة أقل بقليل ، على بيانات الإدخال. لحسن الحظ ، بالنسبة للعتبة d=0.3 التي نحتاجها ، ينجح عدد صغير إلى حد ما من الكائنات في المرور عبر المرشح وتكون مساهمة حسابها في وقت الاستجابة الكلي ضئيلة للغاية بحيث يمكن إهمالها. وإذا كان الأمر كذلك ، فيمكنك توفير أكثر من ذلك بقليل.

النهج الخامس ، والتخلص من التسلسل

عند العمل مع مجموعات كبيرة ، يعد sequence بمثابة دفاع جيد ضد نفاد الذاكرة غير السار للغاية. ومع ذلك ، إذا علمنا بوضوح أنه في المرشح الأول سيتم تخفيض المجموعة إلى حجم عاقل ، فسيكون الخيار الأكثر عقلانية هو استخدام التكرار العادي في حلقة مع إنشاء مجموعة وسيطة ، لأن sequence ليس فقط عصريًا وشابًا ، ولكن أيضًا مكرر ، الذي hasNext الصحابة التالية الذين هم بعيدون عن الأحرار.

 fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } 

يبدو أن السعادة هنا ، لكنني أردت أن "أجعلها جميلة". هنا نأتي إلى قصة مفيدة وعدت.

النهج السادس ، أردنا الأفضل

نكتب على Kotlin ، وهنا بعض java.lang.Long.bitCount الأجنبية! ومؤخرا ، تم جلب أنواع غير موقعة في اللغة. مهاجمة!

لم يقل قال من القيام به. ULong استبدال All ULong بـ ULong ، ULong من مصدر Java ULong إعادة كتابتها كدالة امتداد لـ ULong

 fun ULong.bitCount(): Int { var i = this i = i - (i.shr(1) and 0x5555555555555555uL) i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL) i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL i = i + i.shr(8) i = i + i.shr(16) i = i + i.shr(32) return i.toInt() and 0x7f } 

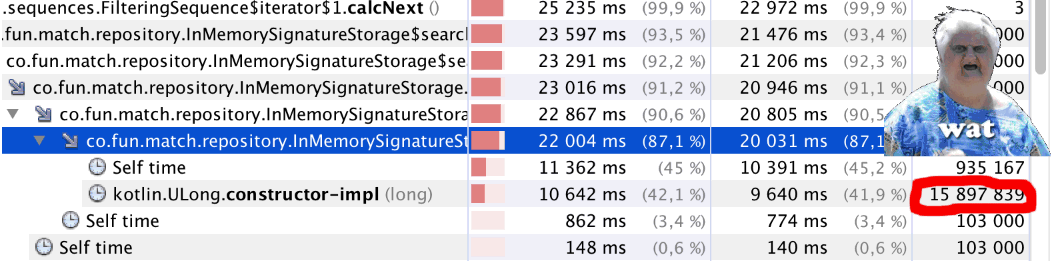
نبدأ و ... هناك خطأ ما. بدأ الرمز للعمل بشكل أبطأ بشكل ملحوظ. نبدأ منشئ ملفات التعريف ونرى شيئًا غريبًا (انظر bitCount() المقالة): أقل قليلاً من مليون مكالمة إلى bitCount() ما يقرب من 16 مليون مكالمة إلى Kotlin.ULong.constructor-impl . ماذا؟

وأوضح اللغز ببساطة - مجرد إلقاء نظرة على رمز فئة ULong

 public inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> { @kotlin.internal.InlineOnly public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data)) @kotlin.internal.InlineOnly public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data)) @kotlin.internal.InlineOnly public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount) @kotlin.internal.InlineOnly public inline operator fun inc(): ULong = ULong(data.inc())  .. } 

لا ، أنا أفهم كل شيء ، ULong هو experimental الآن ، ولكن كيف يتم ذلك؟
بشكل عام ، نحن ندرك أن النهج فشل ، وهو أمر مؤسف.

حسنا ، ولكن لا يزال ، ربما يمكن تحسين شيء آخر؟

في الواقع ، يمكنك ذلك. رمز java.lang.Long.bitCount الأصلي ليس هو الأمثل. إنه يعطي نتيجة جيدة للحالة العامة ، لكن إذا علمنا مقدمًا بمعالجاتنا التي سيعمل بها تطبيقنا ، فيمكننا اختيار طريقة أكثر مثالية - إليك مقالة جيدة جدًا حول هذا الموضوع على Habré. أوصي تمامًا بحساب البتات المفردة .

لقد استخدمت "الطريقة المدمجة"

 fun Long.bitCount(): Int { var n = this n -= (n.shr(1)) and 0x5555555555555555L n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L) n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56) return n.toInt() and 0x7F } 

عد الببغاوات

تم إجراء جميع القياسات بشكل عشوائي ، أثناء التطوير على الجهاز المحلي ويتم إعادة إنتاجها من الذاكرة ، لذلك من الصعب التحدث عن أي دقة ، ولكن يمكنك تقدير المساهمة التقريبية لكل طريقة.

النتائج

• عند التعامل مع معالجة كميات كبيرة من البيانات ، فإن الأمر يستحق إنفاق الوقت على التحليل الأولي. ربما ليس كل هذه البيانات تحتاج إلى معالجة.
• إذا كان يمكنك استخدام التصفية المسبقة الخشنة ، ولكن رخيصة ، فإن هذا يمكن أن يساعد كثيرا.
• السحر قليلا هو كل شيء لدينا. حسنا ، عند الاقتضاء ، بالطبع.
• في بعض الأحيان يكون من المفيد للغاية النظر إلى أكواد مصدر الفئات والوظائف القياسية.

شكرا لاهتمامكم! :)

ونعم ، أن تستمر.