لإرسال رسالة من محطة أساسية إلى جهاز محمول (والعكس) ، يجب على الموجة الكهرومغناطيسية التغلب على عدد كبير من العقبات: الانعكاس ، الانكسار ، الانتثار ، التظليل ، تحولات تردد دوبلر ، وما إلى ذلك. أولاً ، تسمى كل هذه التأثيرات بالضرب (من اللغة الإنجليزية. الضرب - الضرب) - وفقًا للنموذج الرياضي لمثل هذه التأثيرات. وثانيا ، يمكن جمعها تحت المصطلح العام للخبو .

من المعيار إلى المعيار ، ومن جيل إلى جيل ، ومن التكنولوجيا إلى التكنولوجيا ، ناضل العلماء والمهندسون ويكافحون مشكلة تسوية هذه الخبو (تخفيف الخبو).

وبعض الحلول واسعة الانتشار. دعنا نقول أكثر: كلهم تقريبا ، بطريقة أو بأخرى ، يرتبطون بمفهوم التنوع .

مصدر الرسم التوضيحي (لا ، هذا ليس إعلانًا ، بل مجرد مزيج ناجح من المصطلح والقطة المطلوبة).

مثال على هذه الحلول:

قفز التردد - ضد الخبو الانتقائي للتردد ؛
تقدير القناة والمعادلة من خلال التغذية المرتدة - GSM ، لقمع التغييرات في المجال الزمني ؛
تمديد الطيف (UMTS) ؛
إشارات تجريبية (تبدأ بـ UMTS) على الوصلة الهابطة (الوصلة الهابطة) وتتبع الإشارات (تتبع الإشارة) على الوصلة الصاعدة (الوصلة الصاعدة) - لقمع التغييرات في مجال الوقت ؛
OFDM - LTE ، ضد الخبو الانتقائي للتردد ؛
التنوع الزمني ( تشفير تصحيح الأخطاء ) ؛
تنوع الاستقطاب (على جانب المرسل) + إضافات (مجمعات ، على جانب المستقبل) ؛
التنوع المكاني .

آخر هذه التقنيات التي سنعتبرها اليوم جزءًا من موضوع آخر عن MIMO .

ترتيب تنوع الفضاء وكسب مجموعة

أول واحد.

يوجد مثل هذا المفهوم - ترتيب تنوع الفضاء: إذا أمكن جمع نفس المعلومات من اتجاهات مختلفة ، فإن الأمل في استعادتها سيزداد بشكل صحيح. كمثال من الحياة ، يمكننا أن نتخيل جمع معلومات حول الحدث نفسه من مصادر مخبر مستقلة. في الاتصالات اللاسلكية ، يمكننا زيادة هذا الطلب ، بما في ذلك باستخدام MISO أو SIMO أو MIMO .

الحد النظري لهذا التنوع M_TM_R حيث M_T - عدد هوائيات الإرسال ، و M_R - عدد هوائيات الاستقبال. تذكر هذا.

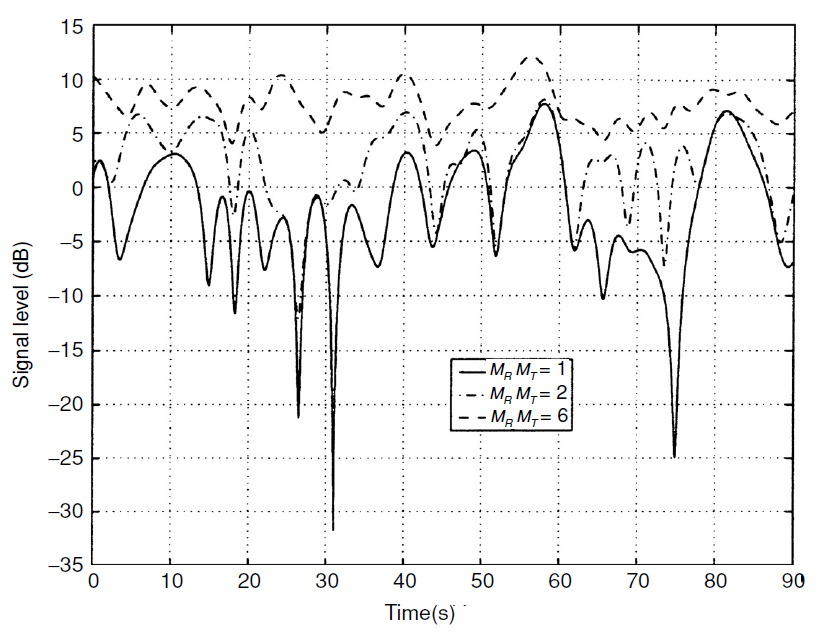
الشكل 1. استقرار القناة الناجم عن زيادة في ترتيب التنوع المكاني. في القيم $M_TM_R \ إلى \ infty$ استقرت القناة تمامًا وستتحول إلى قناة دون أن تتلاشى (AWGN) [1 ، الصفحة 101] .

والثاني.

باستخدام SIMO و MIMO وحتى MISO (في حالة قناة معروفة) ، يمكن للمرء الحصول على ما يسمى كسب الصفيف . هذا يعني أن استخدام هوائيات استقبال متعددة و / أو التوزيع الصحيح للطاقة على جانب الإرسال يمكن أن يزيد من نسبة الإشارة إلى الضوضاء (SNR) - وبالتالي يقلل من عدد الأخطاء.

يمكن الحصول على أوامر التنوع وكسب المصفوفات لمختلف التكوينات تحليليًا [1 ، ص. 86 - 100] وتقليل إلى جدول واحد [1 ، ص. 101] سواء بالنسبة للحالة عندما تكون القناة غير معروفة (CU - قناة غير معروفة) وبالنسبة للحالة عندما تكون القناة معروفة (CK - قناة غير معروفة) على جانب جهاز الإرسال.

ترتيب	ترتيب التنوع	كسب الصفيف
SIMO (CU ، Rx-MRC)
SIMO (CK ، Rx-MRC)
ميسو (CU ، OSTBC)		1
MISO (CK ، Tx-MRC)
MIMO (CU ، OSTBC)
MIMO (CK ، DET)

حسنًا ، حتى مع وجود ضربات عريضة ، ولكن الآن لدينا على الأقل بعض الفهم للجوانب النظرية لقمع التلاشي. والسؤال التالي هو كيفية الوصول إلى هذه الحدود النظرية؟ ما هي تقنيات تفعيل المكاسب المدروسة؟

الحل رقم 1. رموز وقت الفضاء

أحد أكثر فئات حلول التنوع المكاني شيوعًا ، ربما فئة أكواد الزمكان (أكواد الزمكان). على سبيل المثال ، طريقة مألوفة ، على ما أظن ، العديد من طريقة الاموتي (مثال على كود الكود) [2 ، صفحة 40-46]:

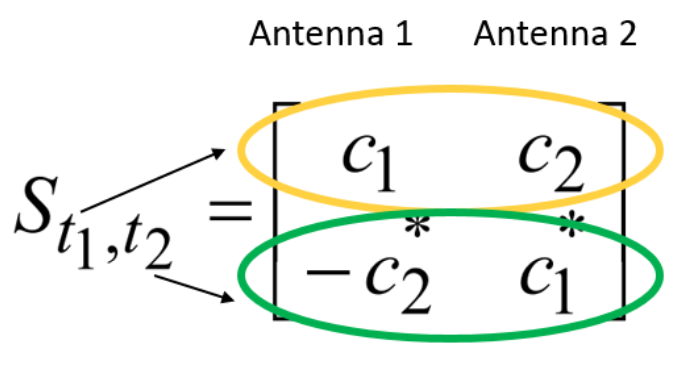
حيث c_i في أنا = 1،2 هي بعض الشخصيات الإدخال t_i في هي فتحات الوقت ، و $\ mathbf {S}$ - هذا ، في الواقع ، مصفوفة الترميز.

مخطط Alamouti متعامد [1 ، الصفحات 93-95 ، 97-98] ، والأهم من ذلك ، لا يتطلب معلومات حالة القناة.

يمكن العثور على الوصف الرياضي لإرسال الإشارة المشفرة بواسطة مخطط Alamouti ، بالإضافة إلى عدة أمثلة لنمذجة هذه التقنية في MatLab في مستودع التخزين الخاص بي . مهتم بالترحيب!

ومع ذلك ، كما ترون ، فإن دائرة Alamouti هي حالة ليس لدينا سوى هوائيات الإرسال ( M_T = 2 ).
لكن لا تفقدي في وقت مبكر: بالطبع ، هناك خيارات أخرى متوفرة ، يطلق عليها ببساطة بطريقة مختلفة قليلاً. على سبيل المثال ، وفقًا لـ [3] ، يمكن تطبيق مخططات الترميز التالية:

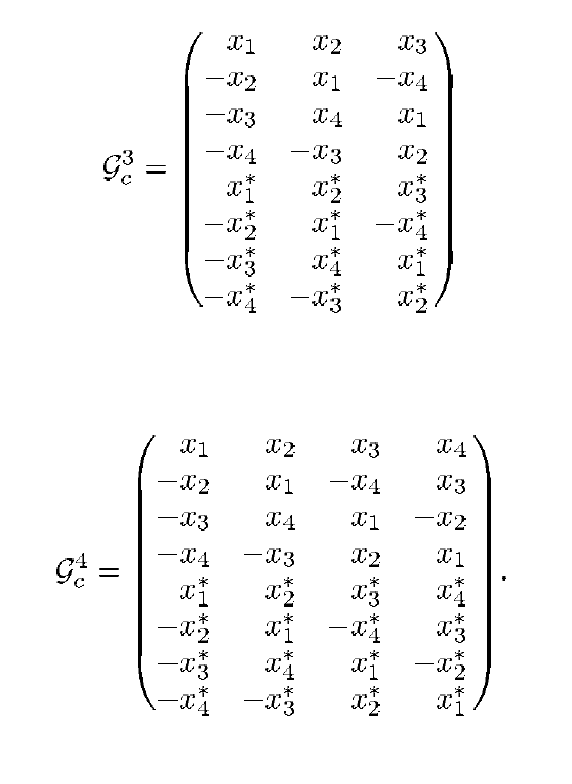
التين. 2. مخططات نقل للحالات و [2].

وهناك العديد من الخيارات الأخرى: فقط لتلبية شروط التعامد.

تتطلب هذه الرموز ، في الواقع ، نفس الإجراءات الخاصة بالتشفير وفك الشفرة كما هو الحال في كود Alamouti. لذلك ، يتم دمجها عادةً تحت المصطلح العام أكواد فضاء الزمان المتعامد (OSTBC - رموز فضاء الوقت الزلزالي Ortogonal).

يتم إيلاء الكثير من الاهتمام لهذه الفئة من الأكواد في المواد "مقدمة في أنظمة MIMO" من MathWorks. أنصح بشدة كل المهتمين بقراءته!

ما هو السعر؟

كما يتضح من مخطط الإرسال ، على الرغم من أننا ننقل الرموز بشكل متوازٍ ، فإننا ننفق عدة فواصل زمنية على هذا. لذلك ، نحن نضحي بالنطاق الترددي (على الأقل ، نحصل عليه أقل). بالنسبة إلى مخطط Alamouti ، فإن هذا الحل الوسط متماثل: نستخدم هوائيات و 2 فجوات زمنية (كما لو كنا نستخدم SISO من حيث النطاق الترددي). قد تؤثر المخططات الأخرى على سرعة النقل بدرجة أكبر.

القرار رقم 2. DET: المهيمن Eigenmode الإرسال

حسنًا ، بالنسبة للفئة السابقة من التقنيات ، لم تكن معرفة القناة مهمة بالنسبة لنا. ولكن ماذا لو كان لا يزال لدينا هذه المعرفة؟ هل هناك أي تقنيات أكثر مناسبة في هذه الحالة؟

في أحد مقالاتي السابقة ، ناقشنا أنه بعد معرفة حالة القناة المتاحة ، يمكننا تطبيق طرق مختلفة لمعالجة الإشارات لزيادة الإنتاجية. نفس المبدأ يعمل على زيادة مناعة الضوضاء.

ربما ، سمع الكثيرون عن طريقة MRC ويعرف الكثيرون أن هذه الطريقة مناسبة جدًا لحالة SIMO ، عندما يكون هناك هوائي واحد على الأقل في الإرسال ، ولكن لا يزال هناك الكثير منهم ، مما يعني أن هناك شيئًا يمكن الجمع بينهما.

لكن ، على الأرجح ، واجه بالفعل عدد أقل من القراء MRC على جانب الإرسال (Tx-MRC) [1 ، ص. 95.96] ، وحتى أقل مع تقنية DET (انتقال المهيمنة Eigenmode) [1 ، ص. 98-100]. إصلاحه!

للبدء ، فكر في الحالة العامة لقناة MIMO وآخر هذه الطرق - DET.

ما هو جوهر:

إذا كان الارسال لديه مصفوفة $\ mathbf {H}$ ثم يمكن معالجتها.
على سبيل المثال ، قم بتحليلها عبر SVD : $\ mathbf {H} = \ mathbf {U} \ mathbf {\ Sigma} \ mathbf {V} ^ H$ وبالتالي الحصول على العديد من مصفوفات خاصية معينة.
يمكن استخدام هذه الخصائص لتحسين النقل ، على سبيل المثال ، باستخدام الترميز المسبق (الترميز المسبق).

نقدم بعض المتجهات المسبقة الترميز:

$\ underset {M_T \ times1} {\ mathbf {w}} = \ sqrt {M_T} \ underset {M_T \ times1} {\ mathbf {v} _1}$

حيث $\ mathbf {v} _1$ هو أول (المهيمنة ، إذا جاز التعبير) ناقلات المصفوفة $\ mathbf {V}$ .

علاوة على ذلك ، يمكننا أيضًا كتابة متجه ما بعد المعالجة:

$\ underset {M_R \ times1} {\ mathbf {g}} = \ underset {M_R \ times1} {\ mathbf {u} _1}$

حيث $\ mathbf {u} _1$ هو أول ناقل للمصفوفة $\ mathbf {U}$ .

أعد تعريف نموذج الإشارة المستقبلة (انظر موضوع النطاق الترددي ):

${z} = \ underset {1 \ times M_R} {\ mathbf {g} ^ H} \ underset {M_R \ times 1} {\ mathbf {y}} = \ mathbf {g} ^ H \ sqrt {\ frac { E_s} {M_T}} \ mathbf {H} \ mathbf {w} s + \ mathbf {g} ^ H \ mathbf {n} = \ sqrt {E_s} \ mathbf {u} _1 ^ H \ mathbf {H} \ mathbf {v} _1 s + \ hat {\ mathbf {n}} = \ sqrt {E_s} \ sigma_ {max} s + \ hat {\ mathbf {n}}$

فويلا! تم تحديد سحر الجبر الخطي بين جميع مسارات التوزيع الأكثر ربحية وتوجيه جميع الطاقة هناك. في الواقع ، لدينا أمامنا خوارزمية تكوين الشعاع الخطي.

على حساب هذا النهج ، تمامًا كما في حالة OSTBC ، فإن حدود النطاق الترددي هي. صحيح ، هذا يحدث الآن بحت في المجال المكاني.

لماذا تحتوي الطريقة على قيم eigen في اسمها إذا كنا نتحدث فقط عن القيم الفردية؟

نظرًا لأن القيم الذاتية (أصل مسارات الانتشار - الخبو) يمكن اشتقاقها مباشرةً من الأرقام الفردية (سعة الخبو):

$\ mathbf {R} _ {\ mathbf {HH} ^ H} = \ mathbf {HH} ^ H = \ mathbf {Q} \ mathbf {\ Lambda} \ mathbf {Q} ^ H = \ mathbf {Q} \ تبدأ {bmatrix} \ lambda_ {max} & & & & \\ &. & & & \\ & &. & & \\ & &. & \\ & & & & \ lambda_ {min} \\ \ end {bmatrix} \ mathbf {Q} ^ H$

حسنًا ، مع DET ، ما هو أكثر أو أقل وضوحًا مع Tx-MRC؟

الأمر أسهل معه - هذه حالة خاصة لـ DET ، والآن سنثبت ذلك.

بالنسبة إلى Tx-MRC ، يقترح متجه الترميز المسبق التالي في الأدبيات:

$\ mathbf {w} = \ sqrt {M_T} \ frac {\ mathbf {h} ^ H} {\ sqrt {|| \ mathbf {h} || ^ 2_F}}$

نضع في اعتبارنا أن مربع قاعدة Frobenius يساوي eigenvalue ، وبالتالي ، مربع الرقم المفرد $|| \ mathbf {h} || ^ 2_F = \ lambda_ {max} = \ sigma ^ 2_ {max}$ (في حالة SIMO و MISO).

ثم نعيد تحديد نموذج الإشارة المستقبلة ، فقط لحالة MISO:

$y = \ sqrt {\ frac {E_s} {M_T}} \ mathbf {h} \ mathbf {w} s + \ mathbf {n} = \ sqrt {\ frac {E_s} {M_T}} \ mathbf {h} \ sqrt {M_T} \ frac {\ mathbf {h} ^ H} {\ sqrt {|| \ mathbf {h} || ^ 2_F}} s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} \ mathbf {h} \ mathbf {h} ^ H s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} || \ mathbf {h } || _F ^ 2 s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} \ lambda_ {max} s + \ mathbf {n}} = \ sqrt {E_s} \ sigma_ {max} s + \ mathbf {n}}$

الذي كان مطلوبا لإثبات.

لاحظ ، الآن نحن نتحدث ليس فقط عن فصل الإشارات على جانب الإرسال والجمع بينها على جانب الاستقبال ، كما كان الحال مع OSTBC. الآن نحن نتحدث عن التوزيع الأمثل للطاقة. هذا يعني أن قيم كسب الصفيف في هذه الحالة أعلى من OSTBC.

الآن بعد أن تم نطق جميع الكلمات ، سنحاول محاكاة تقنياتنا.

تصميم

لقد عدت اليوم قليلاً: بالنسبة لنمذجة OSTBC ، تم استخدام كائنات جاهزة من أدوات الاتصال (MatLab R2014a - أيها كانت):

comm.OSTBCEncoder - تشفير رموز فضاء الزمكان Ortogonal ؛
comm.OSTBCCombiner - مُدمج رموز الكتل الزمنية الزمانية Ortogonal.

من أجل التشكيل وإزالة التشكيل (وحساب الخطأ في البتات - BER) ، لم تعد الدالات تستخدم ، ولكن الدوال . نظائرها في حزمة اوكتاف الاتصالات .

رموز المصدر يمكن العثور عليها هنا.

clear all; close all; clc snapshots = 100000; EbNo = 0:15; M = 2; % modulation order (BPSK) Mt = 2; % num. of Tx antennas Mr = [1; 2]; % num. of Rx antennas ostbcEnc = comm.OSTBCEncoder('NumTransmitAntennas', Mt); % for Alamouti ric_ber = zeros(length(EbNo), length(M), length(Mr)); sum_BER_alam = zeros(length(EbNo), length(M), length(Mr)); sum_BER_det = zeros(length(EbNo), length(M), length(Mr)); for mr = 1:length(Mr) ostbcComb = comm.OSTBCCombiner('NumTransmitAntennas', Mt, 'NumReceiveAntennas', Mr(mr)); H = zeros(Mr(mr), Mt, snapshots); alam_fad_msg = zeros(snapshots, Mr(mr)); for m = 1:length(M) ric_ber(:,m,mr) = berfading(EbNo, 'psk', M(m), Mr(mr)*Mt, 0); snr = EbNo+10*log10(log2(M(m))); % Signal-to-Noise Ratio message = randi([0, M(m)-1],100000,1); mod_msg = pskmod(message, M(m), 0, 'gray'); Es = mean(abs(mod_msg).^2); % symbol energy alam_msg = step(ostbcEnc, mod_msg); % OSTBC encoding % Channel h = (1/sqrt(2))*(randn(Mr(mr),Mt,snapshots/Mt)... + 1j*randn(Mr(mr),Mt, snapshots/Mt)); % Rayleigh flat fading % Channel is stable during to time-slots: H(:,:,1:2:end-1) = h; H(:,:,2:2:end) = h; pathGainself = permute(H,[3,2,1]); % Transmit through the channel (Alamouti): for q = 1:snapshots; alam_fad_msg(q,:) = (sqrt(Es/Mt)*H(:,:,q)*alam_msg(q,:).').'; end % DET: sigmas = zeros(length(mod_msg), 1); for hi = 1:length(mod_msg) [U, Sigma, Vh] = svd(H(:, :, hi)); sigmas(hi) = Sigma(1, 1); end det_fad_msg = mod_msg.*sigmas; No = Es./((10.^(EbNo./10))*log2(M(m))); % Noise spectrum density for c = 1:500 for jj = 1:length(EbNo) alam_noisy_msg = alam_fad_msg + ... sqrt(No(jj)/2)*(randn(size(alam_fad_msg)) + ... 1j*randn(size(alam_fad_msg))); % AWGN alam_decodeData = step(ostbcComb,alam_noisy_msg,pathGainself); %OSTBC combining alam_demod_msg = pskdemod(alam_decodeData, M(m), 0, 'gray'); % demodulation [number,alam_BER(c,jj)] = biterr(message, alam_demod_msg); % BER det_noisy_msg = det_fad_msg+ ... sqrt(No(jj)/2)*(randn(size(mod_msg)) + ... 1j*randn(size(mod_msg))); %AWGN det_decodeData = det_noisy_msg./sigmas; % Zero-Forcing equalization det_demod_msg = pskdemod(det_decodeData, M(m), 0, 'gray'); % demodulation [number,det_BER(c,jj)] = biterr(message, det_demod_msg); % BER end end sum_BER_alam(:,m, mr) = sum(alam_BER)./c; sum_BER_det(:,m, mr) = sum(det_BER)./c; end end figure(1) semilogy(EbNo, sum_BER_alam(:, 1, 1), 'b-o', ... EbNo, sum_BER_det(:,1,1), 'b->',... EbNo, ric_ber(:,1,1), 'b-',... EbNo, sum_BER_alam(:, 1, 2), 'r-o', ... EbNo, sum_BER_det(:,1,2), 'r->',... EbNo, ric_ber(:,1,2), 'r-',... 'LineWidth', 1.5) title('BPSK (Rayleigh flat fading)') legend('Alamouti (2x1)','Tx-MRC (2x1)','2-nd order diversity', ... 'Alamouti (2x2)','DET (2x2)','4-th order diversity') xlabel('EbNo (dB)') ylabel('BER') grid on

يجب أن تتحول إلى شيء مثل هذا:

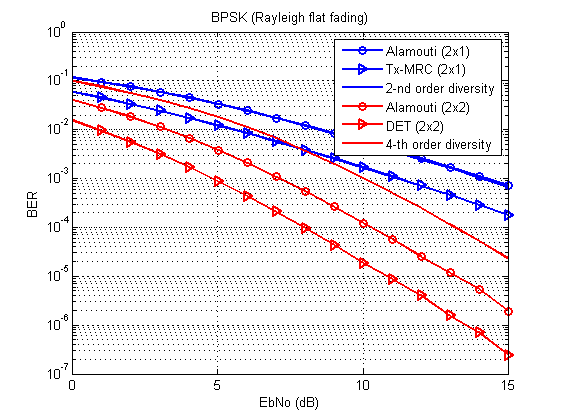
التين. 3. منحنيات خطأ البتات / الرمز لتقنيات الإرسال المختلفة (BPSK ، قناة Rayleigh مع خبو مسطح). قارن مع [1 ، ص. 96 ، 100].

والآن السؤال هو: أين هو منحنى الحد النظري للتنوع من الدرجة الثانية؟

الجواب

كل شيء حسب الجدول: هذا المنحنى يتزامن تمامًا مع Alamouti 2x1. في حالة MIMO ، يأتي كسب الصفيف أيضًا قيد التشغيل ، وبالتالي يتم فصل المنحنيات.

بطريقة أو بأخرى ، ومن المتوقع أن يتفوق DET (أو Tx-MRC) على Alamouti من حيث الجودة.

مثل هذا: المعرفة قوة!

أدب

بولراج ، أروجواسوامي ، روهيت نبار ، ودانانجاي غور. مقدمة في الاتصالات اللاسلكية الزمكان. مطبعة جامعة كامبريدج ، 2003.
Bakulin M.G، Varukina L.A.، Kreindelin V. B. MIMO technology: المبادئ والخوارزميات // M: الخط الساخن - الاتصالات. - 2014.-- T. 244.
Tarokh، V.، Jafarkhani، H.، & Calderbank، AR (1999). رموز كتلة الزمكان من التصاميم المتعامدة. معاملات IEEE على نظرية المعلومات ، 45 (5) ، 1456-1467.

لأعضاء هيئة التدريس والطلاب الأخوة في مهنتي الأم أقول مرحباً!

MIMO التنوع المكاني: Alamouti ، DET ، وغيرها من التنوع المكاني

ترتيب تنوع الفضاء وكسب مجموعة

الحل رقم 1. رموز وقت الفضاء

القرار رقم 2. DET: المهيمن Eigenmode الإرسال

تصميم

أدب

More articles: