مرحبا بالجميع! اسمي ديمتري نوفيكوف ، أنا مطور جافا سكريبت في بنك ألفا ، وسأخبرك اليوم عن تجربتنا في استنباط نوع الإجراء باستخدام Typescript ، وما هي المشاكل التي واجهناها وكيف حلناها.
هذا نسخة من تقريري حول Alfa JavaScript MeetUp. يمكنك رؤية الكود من شرائح العرض التقديمي
هنا ، وتسجيل بث mitap
هنا .
تعمل تطبيقاتنا الأمامية على مجموعة من React + Redux. يبدو أن تدفق البيانات المسترجع يبدو كالتالي:
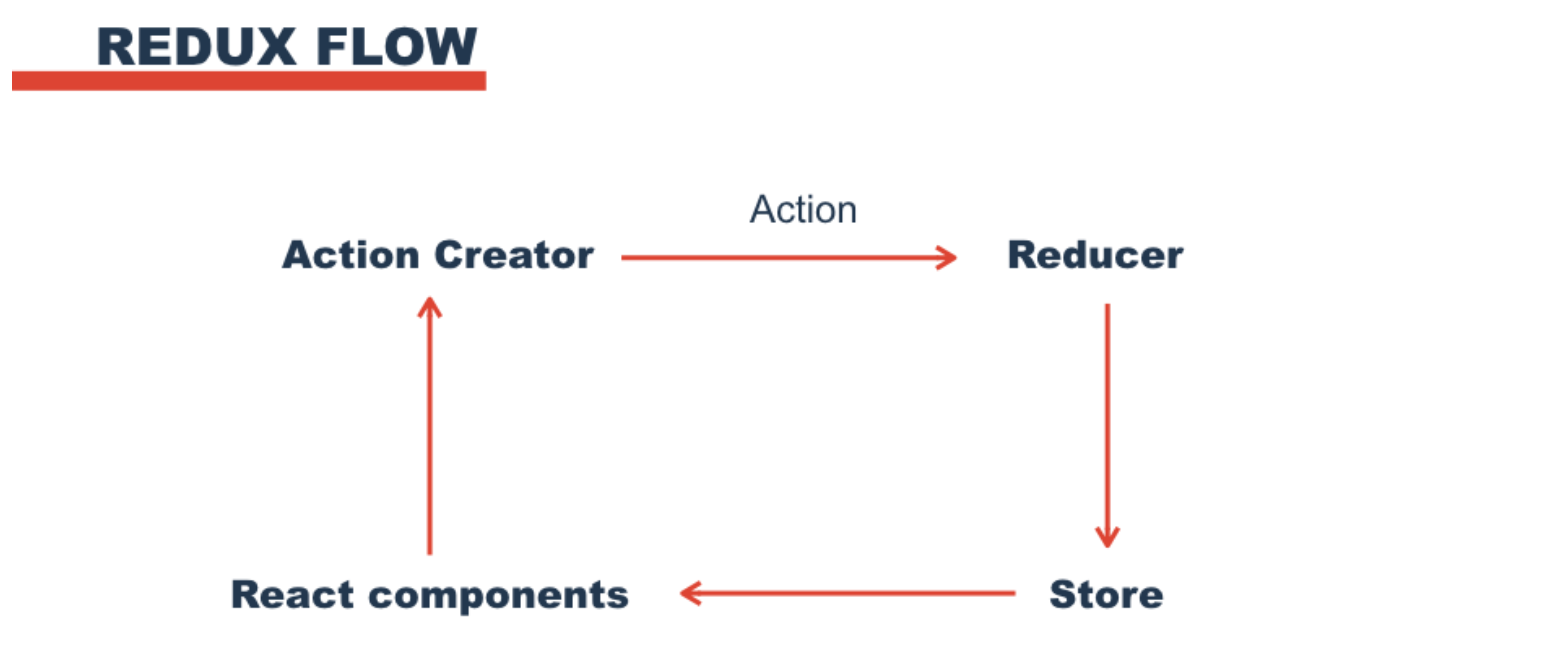
هناك منشئو الإجراءات - وظائف تُرجع إجراءً ما. تقع الإجراءات في المخفض ، ويقوم المخفض بإنشاء جانب جديد يستند إلى القديم. يتم توقيع المكونات على الحفلة ، والتي بدورها يمكنها إرسال إجراءات جديدة - وكل شيء يتكرر.
هذه هي الطريقة التي يظهر بها منشئ الإجراء في الكود:

هذه مجرد وظيفة تُرجع إجراءً - كائن يجب أن يحتوي على حقل سلسلة كتابة وبعض البيانات (اختياري).
هذا ما يشبه المخفض النموذجي:

هذه علبة تبديل عادية تبحث في حقل الكتابة لأحد الإجراءات وتولد جانبًا جديدًا. في المثال أعلاه ، يضيف ببساطة قيم الممتلكات من التصرف هناك.
ماذا لو ارتكبنا خطأ بطريق الخطأ في كتابة المخفض؟ على سبيل المثال ، مثل هذا ، سنقوم بتبادل خصائص الإجراءات المختلفة:

جافاسكريبت لا يعرف شيئًا عن تصرفاتنا ويعتبر هذه الشفرة صالحة تمامًا. ومع ذلك ، لن يعمل كما هو مقصود ، ونود أن نرى هذا الخطأ. ما سوف يساعدنا إن لم يكن Typescript؟ دعونا نحاول وصف تصرفاتنا.

بادئ ذي بدء ، سنكتب أنواع "الجبين" لإجراءاتنا - Action1Type و Action2Type. ثم ، ادمجهم في نوع اتحاد واحد لاستخدامه في المخفض. النهج بسيط ومباشر ، ولكن ماذا لو تغيرت البيانات في الإجراءات أثناء تطوير التطبيق؟ لا تقم بتغيير الأنواع يدويًا في كل مرة. نعيد كتابتها كما يلي:

سيعود عامل التشغيل typeof نوع منشئ الإجراء إلينا ، وسيوفر لنا نوع إرجاع نوع القيمة المرجعة للدالة - أي نوع العمل. نتيجة لذلك ، سوف تتحول إلى نفس الشريحة أعلاه ، ولكن لم تعد يدويًا - عند تغيير الإجراءات ، سيتم تحديث ActionTypes من نوع الاتحاد تلقائيًا. عظيم! نكتبه في المخفض و ...

وعلى الفور نحصل على أخطاء من البرنامج النصي. علاوة على ذلك ، فإن الأخطاء ليست واضحة تمامًا - خاصية البار غير موجودة في الإجراء foo ، كما أن foo غائبة في الشريط ... يبدو أنها الطريقة التي ينبغي أن تكون؟ يبدو أن هناك شيء ما افسدت. بشكل عام ، نهج الجبهة لا يعمل كما هو متوقع.
لكن هذه ليست المشكلة الوحيدة. تخيل أنه مع مرور الوقت ، سوف ينمو تطبيقنا ، وسيكون لدينا الكثير من الإجراءات. كثير

كيف سيكون شكلنا الشائع بالنسبة لهم في هذه الحالة؟ ربما شيء مثل هذا:

وإذا أخذنا في الاعتبار أنه سيتم إضافة الإجراءات وحذفها ، فسوف يتعين علينا دعم كل هذا يدويًا - إضافة وحذف أنواع. هذا أيضا لا يناسبنا على الإطلاق. ما يجب القيام به لنبدأ مع المشكلة الأولى.

لذلك ، لدينا اثنين من منشئي الإجراءات ، والنوع الشائع لهم هو اتحاد أنواع الإجراءات المشتقة تلقائيًا. كل إجراء له خاصية كتابة ، ويتم تعريفه كسلسلة. هذا هو أصل المشكلة. لتمييز إجراء واحد عن آخر ، نحتاج إلى أن يكون كل نوع فريدًا ولا يقبل سوى قيمة فريدة واحدة.

هذا النوع يسمى الحرفي. النوع الحرفي هو من ثلاثة أنواع - رقمية ، سلسلة والمنطقية.

على سبيل المثال ، لدينا النوع onlyNumberOne ونحدد أن المتغير من هذا النوع يمكن أن يكون مساويًا فقط للرقم 1. تعيين 2 - واحصل على خطأ في الكتابة. تعمل السلسلة بطريقة مماثلة - يمكن تعيين قيمة سلسلة واحدة فقط لمتغير. حسنًا ، منطقية إما صحيحة أو خاطئة ، دون غموض.
عام
كيفية حفظ هذا النوع دون السماح له بالتحول إلى سلسلة؟ سوف نستخدم الأدوية الجنيسة. عام مثل هذا التجريد على أنواع. لنفترض أن لدينا وظيفة عديمة الفائدة تأخذ المدخلات كوسيطة وتعيدها بدون تغييرات. كيف يمكنني كتابته؟ اكتب أيًا ، لأنه يمكن أن يكون مطلقًا أي نوع؟ ولكن إذا كان هناك نوع من المنطق في الوظيفة ، فيمكن أن يحدث تحويل الكتابة ، على سبيل المثال ، يمكن أن يتحول الرقم إلى سلسلة ، ولن يتخطى أي الجمع هذا. غير مناسب

عام سيساعدنا على الخروج من هذا الموقف. يعني الإدخال أعلاه أننا نقوم بتمرير وسيطة من نوع معين T إلى الإدخال ، وستعود الوظيفة بنفس النوع من T بالضبط. لا نعرف أيها ستكون - رقم أو سلسلة أو منطقية أو أي شيء آخر - لكن يمكننا ضمان ذلك سيكون بالضبط نفس النوع. هذا الخيار يناسبنا.
دعونا تطوير مفهوم الوراثة قليلا. نحن بحاجة إلى معالجة ليس كل الأنواع بشكل عام ، ولكن سلسلة حرفية ملموسة. هناك كلمة رئيسية تمدد لهذا:

تدوين "T يمتد السلسلة" يعني أن T هو نوع معين ، وهو مجموعة فرعية من نوع السلسلة. تجدر الإشارة إلى أن هذا يعمل فقط مع الأنواع البدائية - إذا بدلاً من استخدام السلسلة ، فإننا نستخدم نوع كائن مع مجموعة محددة من الخصائص ، على العكس من ذلك يعني أن T عبارة عن مجموعة OVER من هذا النوع.
فيما يلي أمثلة على استخدام دالة تمت كتابتها بالامتدادات والأدوية:

- وسيطة سلسلة الكتابة - ستُرجع الدالة السلسلة
- وسيطة من نوع سلسلة حرفية - سوف ترجع الدالة سلسلة حرفية
- إذا لم تبدو الوسيطة كسلسلة ، على سبيل المثال ، رقم أو صفيف ، فسيقوم البرنامج النصي بإعطاء خطأ.
حسنا ، وعموما يعمل.

نحن نستبدل وظيفتنا في نوع الإجراء - إنها تُرجع نفس نوع السلسلة بالضبط ، ولكنها لم تعد سلسلة ، ولكنها سلسلة حرفية ، كما ينبغي أن تكون. نحن نجمع نوع الاتحاد ، ونقوم بتصنيف المخفض - كل شيء على ما يرام. وإذا ارتكبنا خطأ ونكتب الخصائص الخاطئة ، فلن يعطنا النص البرمجي للوقت خطأ اثنين ، بل خطأً منطقيًا ومفهومًا:

دعنا نذهب أبعد من ذلك قليلا وملخص من نوع السلسلة. سنكتب نفس التصنيف ، فقط باستخدام اثنين من الأدوية العامة - T و U. الآن لدينا نوع معين من T سيعتمد على نوع آخر من U ، بدلاً من ذلك يمكننا استخدام أي شيء - على الأقل سلسلة ، على الأقل رقم ، منطقي على الأقل. يتم تطبيق هذا باستخدام وظيفة المجمع:

وأخيراً: المشكلة الموصوفة معلقة لفترة طويلة كمشكلة على github ، وأخيراً ، في Typescript الإصدار 3.4 ، قدم لنا المطورون تأكيدًا على الحل - const. له شكلان من أشكال التسجيل:

وبالتالي ، إذا كان لديك نص جديد ، فيمكنك ببساطة استخدام إما const في الإجراءات ، ولن يتحول النوع الحرفي إلى سلسلة. في الإصدارات الأقدم ، يمكنك استخدام الطريقة الموضحة أعلاه. اتضح أن لدينا الآن ما يصل إلى حلين للمشكلة الأولى. ولكن يبقى الثاني.

لا يزال لدينا الكثير من الإجراءات المختلفة ، وعلى الرغم من حقيقة أننا نعرف الآن كيفية التعامل مع أنواعها بشكل صحيح ، ما زلنا لا نعرف كيفية تجميعها تلقائيًا معًا. يمكننا كتابة اتحاد يدويًا ، ولكن إذا تم حذف الإجراءات وإضافتها ، فلا نزال بحاجة إلى حذفها وإضافتها يدويًا في الكتابة. هذا خطأ

من أين تبدأ؟ افترض أن لدينا منشئي الإجراءات مستوردة معًا من ملف واحد. نود أن نلتف حولهم واحدًا تلو الآخر ، ونستنتج أنواع أفعالهم ونجمعها في نوع اتحاد واحد. والأهم من ذلك ، نود القيام بذلك تلقائيًا ، دون تحرير الأنواع يدويًا.

لنبدأ بالتجول بين المبدعين الفعليين. للقيام بذلك ، هناك نوع معين معين يصف مجموعات قيمة المفتاح. هنا مثال:

يؤدي هذا إلى إنشاء نوع لكائن تكون مفاتيحه option1 و option2 (من مجموعة المفاتيح) ، والقيم صحيحة أو خاطئة. في إصدار أكثر عمومية ، يمكن تمثيل هذا كنوع من mapOfBool - كائن به نوع من مفاتيح الصفوف والقيم المنطقية.
حسنا. ولكن كيف يمكننا التحقق من أنه كائن يتم تقديمه لنا عند الإدخال ، وليس نوعًا آخر؟ النوع الشرطي ، وهو ثلاثية بسيطة في عالم الأنواع ، سوف يساعدنا في هذا.
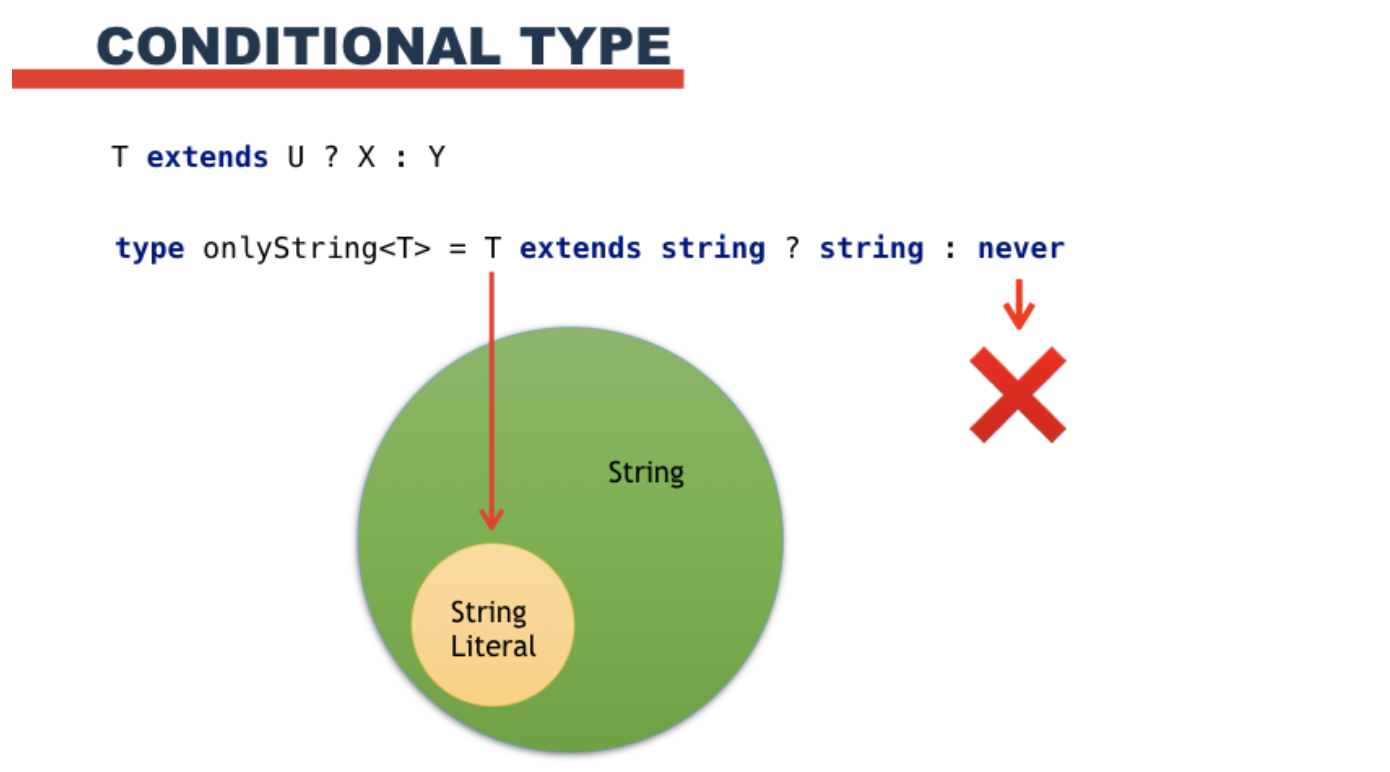
في هذا المثال ، نتحقق: النوع T له شيء مشترك مع السلسلة؟ إذا كانت الإجابة بنعم ، فقم بإرجاع السلسلة ، وإذا لم يكن الأمر كذلك ، لا تعود أبدًا. هذا هو نوع خاص من شأنه أن يعود لنا دائما خطأ. سلسلة حرفية يرضي شرط الثلاثي. فيما يلي بعض نماذج التعليمات البرمجية:

إذا حددنا شيئًا ما في الوراثة لا يشبه السلسلة ، فسوف يعطينا typescript خطأً.
لقد اكتشفنا الحل البديل والتحقق منه ، يبقى فقط الحصول على الأنواع ودمجها في الاتحاد. هذا سوف يساعدنا في الاستدلال على النوع في الكتابة. يعيش Infer عادةً في نوع مشروط ، ويفعل شيئًا كهذا: يمر عبر جميع أزواج القيمة الرئيسية ، ويحاول استنتاج نوع القيمة ومقارنته بالآخرين. إذا كانت أنواع القيم مختلفة ، فإنها تجمعها في اتحاد. فقط ما نحتاجه!

حسنًا ، يبقى الآن أن نضعها معًا.
اتضح هذا التصميم:

المنطق هو ما يلي تقريبًا: إذا بدا T ككائن يحتوي على بعض مفاتيح السلسلة (منشئو الإجراءات) ، ولهم قيم من نوع ما (دالة ستُرجع الإجراء إلينا) ، ثم حاول تجاوز هذه الأزواج ، واستنتج نوع هذه القيم والحد من النوع الشائع. وإذا حدث خطأ ما - قم برمي خطأ خاص (اكتب أبدًا).
إنه صعب فقط للوهلة الأولى. في الواقع ، كل شيء بسيط للغاية. يجدر الانتباه إلى ميزة مثيرة للاهتمام - نظرًا لحقيقة أن كل إجراء يحتوي على حقل كتابة فريد ، فإن أنواع هذه الإجراءات لن تلتصق ببعضها البعض ، ونحصل على نوع اتحاد كامل في المخرجات. إليك ما يبدو في الكود:

نحن نستورد منشئي الإجراءات كإجراءات ، ونأخذ ReturnType (نوع قيمة الإرجاع هو الإجراءات) ، ونجمعها باستخدام نوعنا الخاص. اتضح فقط ما هو مطلوب.

ما هي النتيجة؟ حصلنا على اتحاد من الأنواع الحرفية لجميع الإجراءات. عند إضافة إجراء جديد ، يتم تحديث النوع تلقائيًا. نتيجة لذلك ، حصلنا على كتابة صارمة كاملة من الإجراءات ، والآن لا يمكننا ارتكاب خطأ. حسنًا ، على طول الطريق ، علمنا بالأدوية العامة ، والنوع الشرطي ، والنوع المعين ، ولا نستنتج أبدًا - يمكنك الحصول على مزيد من المعلومات حول هذه الأدوات
هنا .