نعلم جميعًا شكل علامة التجزئة ، ولكن هل تساءلت يومًا عن عدد مرات العثور على شخصية معينة في علامة التجزئة؟ لقد تساءلت. وقررت التحقق. رسمت نصا بيثون لحساب ، وهنا ما جاء منه.
أولاً ، قمت بإنشاء سلسلة عشوائية من الأحرف (الطول من 0 إلى 1000).
def random_string(from_int, to_int): return str(''.join(random.SystemRandom().choice(string.ascii_letters + string.digits + string.punctuation) for _ in range(random.randint(from_int, to_int))))
بعد ذلك ، أخذت تجزئة MD5 من السلسلة.
def md5_from_string(string): return hashlib.md5(string.encode('utf-8')).hexdigest()
بعد - حسبت عدد الأرقام من 0 إلى 9 في التجزئة. على عينة من 1000 تجزئة ، تلقيت البيانات التالية:
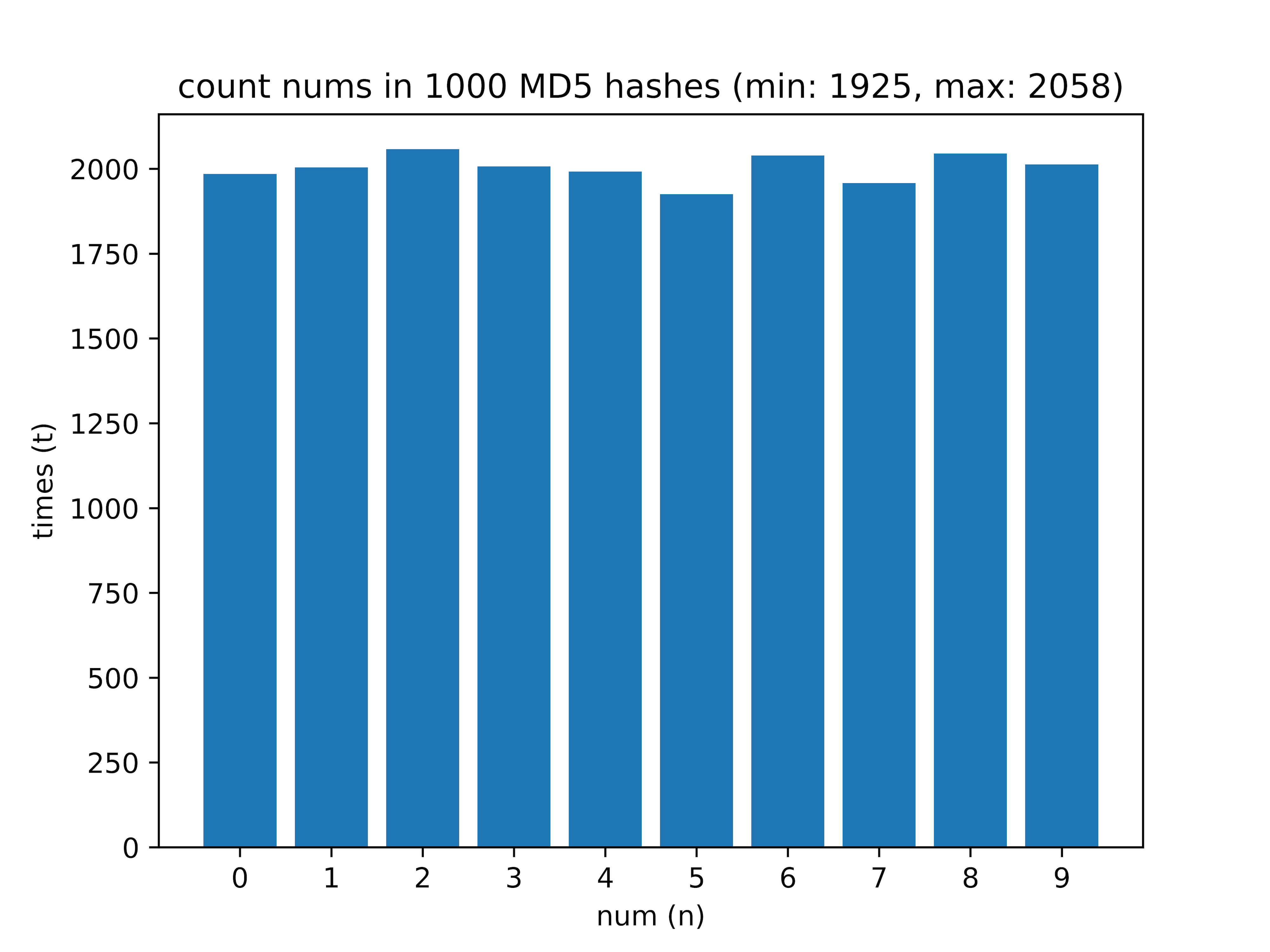
هنا يعتبر الاختلاف بين الأرقام الأكثر شيوعًا والأكثر ندرة (قيمة دلتا) أمرًا مثيرًا للاهتمام.

علاوة على ذلك ، من أجل تتبع التغير في قيمة الدلتا ، قدم عينات من 10000 ، 100000 ، 1،000،000 ، 100،000،000 التجزئة.

فيما يلي قائمة تحتوي على قيم الحد الأدنى والحد الأقصى للأرقام وقيمة دلتا على العينات بأرقام مختلفة من تجزئة MD5:
- 100 - دقيقة: 179 ، بحد أقصى: 230 ، دلتا: 22.17 ٪
- 1000 - الحد الأدنى: 1925 ، الحد الأقصى: 2058 ، الدلتا: 6.46 ٪
- 10000 - الحد الأدنى: 19769 ، الحد الأقصى: 20251 ، الدلتا: 2.38 ٪
- 100000 - الحد الأدنى: 199297 ، الحد الأقصى: 200846 ، الدلتا: 0.77 ٪
- 1،000،000 - الحد الأدنى: 1997650 ، الحد الأقصى: 2001690 ، الدلتا: 0.20 ٪
- 10000000 - الحد الأدنى: 19991830 ، الحد الأقصى: 20004818 ، الدلتا: 0.06 ٪
ما لدينا: مع زيادة عدد التجزئات في الصفيف ، تنخفض قيمة الدلتا وستقع أي أرقام ذات الاحتمال نفسه تقريبًا في الصفيف. وبالتالي ، كلما كانت العينة أكبر ، كان الفرق بين الأرقام التي يتم مواجهتها بشكل متكرر ونادراً ما يشاهد. وفقًا لذلك ، فإن احتمال الحصول على رقم معين في علامة التجزئة يميل إلى التوحيد.
شكلت هذه المعلومات أساس الخوارزمية التي
طبقناها على منصة المنافسة
bepeam.com