مقدمة في التعلم الآلي

يمكن العثور على الدورة الكاملة باللغة الروسية على هذا الرابط .
دورة اللغة الإنجليزية الأصلية متاحة على هذا الرابط .



ومن المقرر محاضرات جديدة كل 2-3 أيام.

مقابلة مع سيباستيان ترون ، الرئيس التنفيذي لشركة Udacity

"مرحبًا مرة أخرى ، أنا بيج وأنت ضيفتي اليوم ، سيباستيان."
- مرحبا ، أنا سيباستيان!
- ... رجل لديه مهنة لا تصدق ، تمكن من القيام بالكثير من الأشياء المدهشة! أنت أحد مؤسسي Udacity ، وقمت بتأسيس Google X ، وأنت أستاذ في Stanford. لقد قمت بإجراء بحث لا يصدق والتعلم العميق طوال حياتك المهنية. ما الذي جعلك تشعر بالرضا وبأكثر المجالات التي تلقيت فيها أكبر المكافآت على العمل المنجز؟
- بصراحة ، أحب حقًا أن أكون في وادي السيليكون! أحب أن أكون بجانب أشخاص أكثر ذكاءً مني ، وكنت دائماً أعتبر التكنولوجيا كأداة تغير قواعد اللعبة بطرق مختلفة - من التعليم إلى الخدمات اللوجستية والرعاية الصحية ، إلخ. كل هذا يتغير بسرعة ، وهناك رغبة لا تصدق في أن تكون مشاركًا في هذه التغييرات ، لمراقبة هذه التغييرات. نظرت إلى محيطك وتفهم أن معظم ما تراه من حولك لا يعمل كما ينبغي - يمكنك دائمًا ابتكار شيء جديد!
- حسنًا ، هذه رؤية متفائلة جدًا للتكنولوجيا! ما كان أكبر يوريكا طوال حياتك المهنية؟
- يا رب ، كان هناك الكثير! أتذكر أحد الأيام التي اتصل بي فيها لاري بيج واقترح إنشاء سيارات الطيار الآلي التي يمكن أن تقود في جميع شوارع كاليفورنيا. في ذلك الوقت كنت أعتبر خبيراً ، لقد صُنفت بين هؤلاء ، وكنت الشخص نفسه الذي قال "لا ، لا يمكن القيام بذلك". بعد ذلك ، أقنعني لاري أنه من حيث المبدأ ، من الممكن القيام بذلك ، عليك فقط أن تبدأ وتجرب. وفعلنا ذلك! كانت هذه هي اللحظة التي أدركت فيها أنه حتى الخبراء مخطئون وقولوا "لا" ، نحن متشائمون بنسبة 100٪. أعتقد أننا يجب أن نكون أكثر انفتاحًا على الجديد.
- أو ، على سبيل المثال ، إذا اتصل بك لاري بايج وقال: "مرحبًا ، افعل شيئًا رائعًا مثل Google X" وستحصل على شيء رائع!
- نعم ، هذا بالتأكيد ، لا داعي للشكوى! أعني ، كل هذا عملية تمر بالكثير من النقاش حول طريقة التنفيذ. أنا محظوظ حقًا للعمل وأنا فخور بذلك ، على Google X وفي مشاريع أخرى.
- رائع! لذلك ، هذه الدورة تدور حول العمل مع TensorFlow. هل لديك خبرة في استخدام TensorFlow أو ربما كنت على دراية (مسموعة) به؟
- نعم! أنا أحب حرفيا TensorFlow ، بالطبع! في مختبري الخاص ، نستخدمه كثيرًا والكثير ، تم إصدار واحد من أهم الأعمال المستندة إلى TensorFlow قبل عامين تقريبًا. لقد تعلمنا أن iPhone و Android يمكن أن يكونا أكثر فعالية في اكتشاف سرطان الجلد من أفضل أطباء الأمراض الجلدية في العالم. نشرنا بحثنا في الطبيعة وهذا خلق نوع من الضجة في الطب.
- هذا يبدو مذهلا! أنت تعرف وتحب TensorFlow ، وهو أمر رائع بحد ذاته! هل عملت بالفعل مع TensorFlow 2.0؟
- لا ، للأسف لم يتح لي الوقت بعد.
- سيكون مذهلاً! سيعمل جميع الطلاب في هذه الدورة مع هذا الإصدار.
- أنا أحسدهم! بالتأكيد سأحاول ذلك!
- عظيم! في مساقنا الدراسي ، يوجد الكثير من الطلاب الذين لم يشاركوا في التعلم الآلي مطلقًا ، من كلمة "بالكامل". بالنسبة لهم ، قد يكون الحقل جديدًا ، وربما يكون هذا البرنامج جديدًا بالنسبة لشخص ما. ما النصيحة التي لديك بالنسبة لهم؟
- أتمنى أن يظلوا منفتحين - للأفكار والتقنيات والحلول والمواقف الجديدة. التعلم الآلي هو في الواقع أسهل من البرمجة. في عملية البرمجة ، تحتاج إلى مراعاة كل حالة في البيانات المصدر ، وتكييف منطق البرنامج والقواعد لذلك. في هذا الوقت بالذات ، باستخدام TensorFlow والتعلم الآلي ، تقوم أساسًا بتدريب الكمبيوتر باستخدام أمثلة ، مما يتيح للكمبيوتر العثور على القواعد بنفسه.
- هذا مثير للاهتمام بشكل لا يصدق! لا أستطيع الانتظار لإخبار الطلاب في هذه الدورة التدريبية أكثر قليلاً عن التعلم الآلي! سيباستيان ، شكرًا لك على الوقت الذي قضيته في القدوم إلينا اليوم!
- شكرا لك! ابقى على اتصال

ما هو التعلم الآلي؟

لذلك ، لنبدأ بالمهمة التالية - قيم الإدخال والإخراج المقدمة.



عندما يكون لديك القيمة 0 كقيمة الإدخال ، ثم 32 كقيمة الإخراج ، وعندما يكون لديك 8 كقيمة الإدخال ، ثم 46.4 كقيمة الإخراج. عندما يكون لديك 15 كقيمة إدخال ، ثم 59 كقيمة إخراج ، وهكذا.

نلقي نظرة فاحصة على هذه القيم واسمحوا لي أن أطرح عليك سؤالا. يمكنك تحديد ما سيكون الناتج إذا حصلنا على 38 في المدخلات؟



إذا أجبت 100.4 ، فأنت على حق!



لذلك ، كيف يمكننا حل هذه المشكلة؟ إذا نظرت عن كثب إلى القيم ، يمكنك أن ترى أنها مرتبطة بالتعبير:



حيث C - درجة مئوية (قيم الإدخال) ، F - فهرنهايت (قيم الإخراج).

ما فعله دماغك للتو - قارن قيم المدخلات وقيم المخرجات ووجد نموذجًا مشتركًا (الاتصال والاعتماد) بينها - هذا ما يفعله التعلم الآلي.

بناءً على قيم المدخلات والمخرجات ، ستجد خوارزميات التعلم الآلي خوارزمية مناسبة لتحويل قيم المدخلات إلى قيم الإخراج. يمكن تمثيل ذلك على النحو التالي:



لنلقِ نظرة على مثال. تخيل أننا نريد تطوير برنامج يحول الدرجات المئوية إلى درجات فهرنهايت باستخدام الصيغة F = C * 1.8 + 32 .



الحل ، عند الاقتراب من وجهة نظر تطوير البرمجيات التقليدية ، يمكن تنفيذه بأي لغة برمجة باستخدام الوظيفة:



إذن ماذا لدينا؟ تأخذ الدالة قيمة إدخال C ، ثم تحسب قيمة إخراج F باستخدام خوارزمية صريحة ، ثم تُرجع القيمة المحسوبة.



من ناحية أخرى ، في نهج التعلم الآلي ، لدينا فقط قيم المدخلات والمخرجات ، ولكن ليس الخوارزمية نفسها:



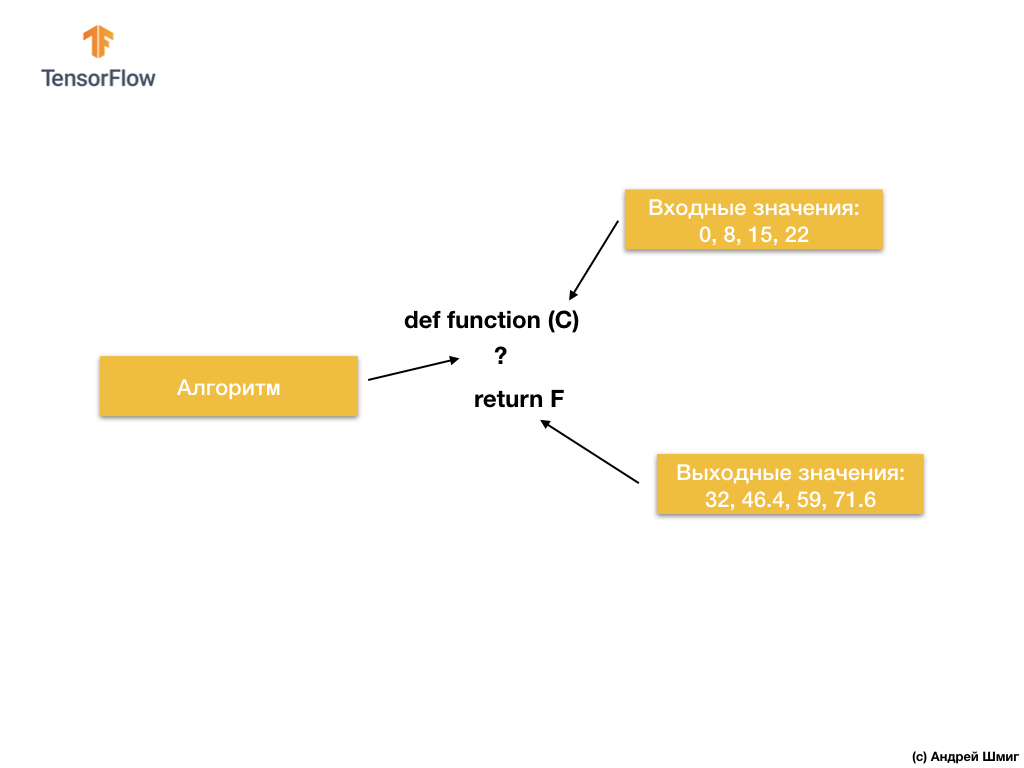
يعتمد أسلوب التعلم الآلي على استخدام الشبكات العصبية لإيجاد العلاقة بين قيم المدخلات والمخرجات.



يمكنك أن تفكر في الشبكات العصبية باعتبارها مجموعة من الطبقات ، كل منها يتكون من الرياضيات المعروفة سابقًا (الصيغ) والمتغيرات الداخلية. تدخل قيمة الإدخال في الشبكة العصبية وتمر عبر مجموعة من طبقات الخلايا العصبية. أثناء المرور عبر الطبقات ، يتم تحويل قيمة الإدخال وفقًا للرياضيات (صيغ معينة) وقيم المتغيرات الداخلية للطبقات ، مما ينتج عنه قيمة إخراج.

لكي تكون الشبكة العصبية قادرة على تعلم وتحديد العلاقة الصحيحة بين قيم المدخلات والمخرجات ، نحتاج إلى تدريبها - للتدريب.

نقوم بتدريب الشبكة العصبية من خلال المحاولات المتكررة لمطابقة قيم الإدخال لإخراج القيم.



في عملية التدريب ، يتم إجراء "تحديد" (اختيار) قيم المتغيرات الداخلية في طبقات الشبكة العصبية حتى تتعلم الشبكة إنشاء قيم الإخراج المقابلة لقيم الإدخال المقابلة.

كما سنرى لاحقًا ، من أجل تدريب شبكة عصبية والسماح لها بتحديد أنسب القيم للمتغيرات الداخلية ، يتم إجراء الآلاف أو عشرات الآلاف من التكرارات (التدريبات).



كإصدار مبسط من فهم التعلم الآلي ، يمكنك تخيل خوارزميات التعلم الآلي كوظائف تحدد قيم المتغيرات الداخلية بحيث تتوافق قيم الإدخال الصحيحة مع قيم المخرجات الصحيحة.

هناك العديد من أنواع هياكل الشبكات العصبية. ومع ذلك ، بغض النظر عن البنية التي تختارها ، فإن الرياضيات في الداخل (أي الحسابات التي يتم تنفيذها وبأي ترتيب) ستبقى دون تغيير أثناء التدريب. بدلاً من تغيير الرياضيات ، تتغير المتغيرات الداخلية (الأوزان والإزاحة) أثناء التدريب.

على سبيل المثال ، في مهمة التحويل من الدرجات المئوية إلى فهرنهايت ، يبدأ النموذج بضرب قيمة الإدخال برقم معين (الوزن) وإضافة قيمة أخرى (الإزاحة). يتمثل التدريب النموذجي في إيجاد قيم مناسبة لهذه المتغيرات ، دون تغيير عمليات الضرب والإضافة.

ولكن شيء واحد رائع للتفكير! إذا كنت قد قمت بحل مشكلة تحويل الدرجات المئوية إلى فهرنهايت ، وهو ما يشار إليه في الفيديو وفي النص أدناه ، فربما تكون قد قمت بحلها لأن لديك بعض الخبرة السابقة أو المعرفة حول كيفية إجراء هذا النوع من التحويل من الدرجات المئوية إلى فهرنهايت. على سبيل المثال ، قد تعرف أن 0 درجة مئوية تقابل 32 درجة فهرنهايت. من ناحية أخرى ، لا تملك النظم المعتمدة على التعلم الآلي معرفة داعمة سابقة لحل المشكلة. يتعلمون حل مثل هذه المشاكل التي لا تستند إلى المعرفة السابقة وفي غيابها الكامل.

كلام كافي - انتقل إلى الجزء العملي من المحاضرة!

CoLab: تحويل درجة مئوية إلى درجة فهرنهايت

النسخة الروسية من شفرة المصدر CoLab والنسخة الإنجليزية من شفرة المصدر CoLab .

الأساسيات: تعلم النموذج الأول

مرحبًا بك في CoLab ، حيث سنقوم بتدريب أول نموذج تعلُّم آلي!

سنحاول الحفاظ على بساطة المواد المقدمة وإدخال فقط المفاهيم الأساسية اللازمة للعمل. سيحتوي CoLabs اللاحق على تقنيات أكثر تقدمًا.

المهمة التي سنحلها هي تحويل الدرجات المئوية إلى فهرنهايت. صيغة التحويل كالتالي:

$$

$$f = c \ times 1.8 + 32$$

بالطبع ، سيكون من الأسهل فقط كتابة وظيفة تحويل في Python أو أي لغة برمجة أخرى تؤدي حسابات مباشرة ، ولكن في هذه الحالة لن يكون التعلم الآلي :)

بدلاً من ذلك ، نحن نتغذى على مدخلات TensorFlow لدينا درجات المدخلات المتاحة درجة مئوية (0 ، 8 ، 15 ، 22 ، 38) ودرجات فهرنهايت المقابلة (32 ، 46 ، 59 ، 72 ، 100). ثم سنقوم بتدريب النموذج بطريقة تتوافق مع الصيغة أعلاه تقريبًا.

استيراد التبعيات

أول شيء TensorFlow هو TensorFlow . هنا وفي ما يلي نسميها اختصارًا tf . نحن أيضا تكوين مستوى تسجيل - الأخطاء فقط.

بعد ذلك ، قم باستيراد NumPy كـ np . Numpy يساعدنا على تقديم بياناتنا Numpy عالية الأداء.

 from __future__ import absolute_import, division, print_function, unicode_literals import tensorflow as tf tf.logging.set_verbosity(tf.logging.ERROR) import numpy as np 

إعداد بيانات التدريب

كما رأينا سابقًا ، تعتمد تقنية التعلم الآلي مع المعلم على البحث عن خوارزمية لتحويل بيانات الإدخال إلى الإخراج. نظرًا لأن مهمة هذا CoLab هي إنشاء نموذج يمكن أن ينتج نتيجة تحويل الدرجات المئوية إلى درجات فهرنهايت ، سنقوم بإنشاء قائمتين - celsius_q و celsius_q ، والتي نستخدمها عند تدريب نموذجنا.

 celsius_q = np.array([-40, -10, 0, 8, 15, 22, 38], dtype=float) fahrenheit_a = np.array([-40, 14, 32, 46, 59, 72, 100], dtype=float) for i,c in enumerate(celsius_q): print("{}   = {}  ".format(c, fahrenheit_a[i])) 

-40.0 = -40.0
-10.0 = 14.0
0.0 = 32.0
8.0 = 46.0
15.0 = 59.0
22.0 = 72.0
38.0 = 100.0

بعض مصطلحات التعلم الآلي:

• الخاصية هي قيمة (قيم) الإدخال الخاصة بنموذجنا. في هذه الحالة ، تكون قيمة الوحدة هي درجة مئوية.
• التسميات هي قيم المخرجات التي يتوقعها نموذجنا. في هذه الحالة ، تكون قيمة الوحدة هي درجة فهرنهايت.
• مثال على ذلك هو زوج من قيم المدخلات والمخرجات المستخدمة للتدريب. في هذه الحالة ، هذا زوج من القيم من celsius_q و celsius_q تحت فهرس معين ، على سبيل المثال ، (22،72).

إنشاء نموذج

بعد ذلك نقوم بإنشاء نموذج. سوف نستخدم النموذج الأكثر بساطة - نموذج شبكة متصلة بالكامل (شبكة Dense ). نظرًا لأن المهمة تافهة جدًا ، ستتكون الشبكة أيضًا من طبقة واحدة مع خلية واحدة.

بناء الشبكة

سنقوم بتسمية الطبقة l0 ( l ayer والصفر) وإنشائها عن طريق تهيئة tf.keras.layers.Dense باستخدام المعلمات التالية:

• input_shape=[1] - تحدد هذه المعلمة بُعد معلمة الإدخال - قيمة واحدة. مصفوفة 1 × 1 بقيمة واحدة. نظرًا لأن هذه هي الطبقة الأولى (والوحيدة) ، فإن بُعد بيانات الإدخال يتوافق مع بُعد النموذج بأكمله. القيمة الوحيدة هي قيمة النقطة العائمة التي تمثل الدرجات المئوية.
• units=1 - تحدد هذه المعلمة عدد الخلايا العصبية في الطبقة. يحدد عدد الخلايا العصبية عدد متغيرات الطبقة الداخلية التي سيتم استخدامها للتدريب على إيجاد حل للمشكلة. نظرًا لأن هذه هي الطبقة الأخيرة ، فإن بُعدها يساوي بعد النتيجة - قيمة إخراج النموذج - رقم نقطة عائمة مفرد يمثل الدرجات فهرنهايت. (في شبكة متعددة الطبقات ، يجب أن يتناسب حجم وشكل طبقة input_shape مع حجم وشكل الطبقة التالية).

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) 

تحويل الطبقات إلى نموذج

بمجرد تعريف الطبقات ، يجب تحويلها إلى نموذج. يأخذ النموذج Sequential قائمة الطبقات بالترتيب الذي يجب تطبيقه عليها - من قيمة الإدخال إلى قيمة الإخراج.

نموذجنا لديه طبقة واحدة فقط - l0 .

 model = tf.keras.Sequential([l0]) 

تعليق
في كثير من الأحيان ، سوف تواجه تعريف الطبقات مباشرة في وظيفة النموذج ، بدلاً من الوصف الأولي والاستخدام اللاحق:

 model = tf.keras.Sequential([ tf.keras.layers.Dense(units=1, input_shape=[1]) ]) 

نحن تجميع نموذج مع وظيفة الخسارة والتحسين

قبل التدريب ، يجب تجميع النموذج (تجميعه). عند الترجمة للتدريب ، فأنت بحاجة إلى:

• دالة الخسارة - طريقة لقياس مدى القيمة المتوقعة من قيمة المخرجات المرغوبة (يسمى الفرق القابل للقياس "الخسارة").
• وظيفة التحسين - طريقة لضبط المتغيرات الداخلية لتقليل الخسائر.

 model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) 

تُستخدم وظيفة الخسارة ووظيفة التحسين أثناء التدريب النموذجي ( model.fit(...) المذكور أدناه) لإجراء العمليات الحسابية الأولية في كل نقطة ثم تحسين القيم.

إن إجراء حساب الخسائر الحالية والتحسين اللاحق لهذه القيم في النموذج هو بالضبط ما هو التدريب (تكرار واحد).

أثناء التدريب ، يتم استخدام وظيفة التحسين لحساب التعديلات على قيم المتغيرات الداخلية. الهدف من ذلك هو ضبط قيم المتغيرات الداخلية بهذه الطريقة في النموذج (وهذا ، في الواقع ، دالة رياضية) بحيث تعكس بأكبر قدر ممكن التعبير الموجود لتحويل الدرجات المئوية إلى درجات فهرنهايت.

يستخدم TensorFlow تحليلًا رقميًا لإجراء هذه الأنواع من عمليات التحسين ، وكل هذا التعقيد مخفي عن أعيننا ، لذلك لن ندخل في التفاصيل في هذه الدورة.

ما هو مفيد لمعرفة هذه الخيارات:

تعتبر وظيفة الفقد (خطأ قياسي) ووظيفة التحسين (آدم) المستخدمة في هذا المثال قياسية لهذه النماذج البسيطة ، ولكن هناك العديد من النماذج الأخرى المتاحة بجانبها. في هذه المرحلة ، لا نهتم بكيفية عمل هذه الوظائف.

ما يجب الانتباه إليه هو وظيفة التحسين والمعلمة هي معامل learning rate ، والذي في مثالنا هو 0.1 . هذا هو حجم الخطوة المستخدم عند ضبط القيم الداخلية للمتغيرات. إذا كانت القيمة صغيرة جدًا ، فسيتطلب الأمر العديد من التكرارات التدريبية لتدريب النموذج. الكثير - قطرات الدقة. يتطلب إيجاد قيمة جيدة لمعامل معدل التعلم بعض التجربة والخطأ ، وعادة ما يقع في النطاق من 0.01 (افتراضيًا) إلى 0.1 .

نحن ندرب النموذج

ويتم تدريب النموذج من خلال طريقة fit .

أثناء التدريب ، يتلقى النموذج درجات مئوية عند الإدخال ، ويقوم بإجراء التحويلات باستخدام قيم المتغيرات الداخلية (تسمى "الأوزان") ويعيد القيم التي يجب أن تتوافق مع درجات فهرنهايت. نظرًا لتعيين القيم الأولية للأوزان بشكل تعسفي ، فإن القيم الناتجة ستكون بعيدة عن القيم الصحيحة. يتم احتساب الفرق بين النتيجة المرغوبة والفعلية باستخدام دالة الخسارة ، وتحدد وظيفة التحسين كيفية ضبط الأوزان.

يتم التحكم في هذه الدورة من العمليات الحسابية والمقارنات والتعديلات في طريقة fit . الوسيطة الأولى هي قيمة الإدخال ، الوسيطة الثانية هي قيمة الإخراج المطلوبة. تحدد حجة epochs عدد المرات التي يجب أن تكتمل فيها هذه الدورة التدريبية. تتحكم الوسيطة verbose في مستوى التسجيل.

 history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") 

في مقاطع الفيديو التالية ، سنبحث في تفاصيل كيفية عمل كل هذا وكيف بالضبط الطبقات المتصلة بالكامل (الطبقات Dense ) "تحت الغطاء".

عرض إحصائيات التدريب

تقوم طريقة القياس بإرجاع كائن يحتوي على معلومات حول التغييرات في الخسائر مع كل تكرار لاحق. يمكننا استخدام هذا الكائن لإنشاء جدول خسائر مناسب. تعني الخسارة العالية أن درجات فهرنهايت التي تنبأ بها النموذج بعيدة عن القيم الحقيقية في مجموعة fahrenheit_a .

للتصور ، سوف نستخدم Matplotlib . كما ترون ، فإن نموذجنا يتحسن بسرعة كبيرة في البداية ، ثم يأتي إلى تحسن مستقر وبطيء حتى تصبح النتائج "قريبة" - مثالية في نهاية التدريب.

 import matplotlib.pyplot as plt plt.xlabel('Epoch') plt.ylabel('Loss') plt.plot(history.history['loss']) 

نستخدم النموذج للتنبؤات.

الآن لدينا نموذج تم تدريبه على قيم المدخلات celsius_q وقيم celsius_q لتحديد العلاقة بينهما. يمكننا استخدام طريقة التنبؤ لحساب درجات فهرنهايت التي لم نكن نعرف سابقًا الدرجات المئوية المقابلة لها.

على سبيل المثال ، كم تبلغ 100.0 درجة فهرنهايت؟ حاول أن تخمن قبل تشغيل الكود أدناه.

 print(model.predict([100.0])) 

الاستنتاج:

[[211.29639]]


الإجابة الصحيحة هي 100 × 1.8 + 32 = 212 ، لذلك كان نموذجنا جيدًا!

مراجعة

• لقد أنشأنا نموذجًا باستخدام طبقة Dense .
• قمنا بتدريبها على 3500 مثال (7 أزواج من القيم ، 500 تكرار تدريب)

قام نموذجنا بتعديل قيم المتغيرات الداخلية (الأوزان) في الطبقة Dense بطريقة تُرجع القيم الصحيحة لدرجات فهرنهايت إلى قيمة إدخال تعسفية بالدرجات مئوية.

نحن ننظر إلى الأوزان

دعنا نعرض قيم المتغيرات الداخلية للطبقة Dense .

 print("   : {}".format(l0.get_weights())) 

الاستنتاج:

    : [array([[1.8261501]], dtype=float32), array([28.681389], dtype=float32)] 

قيمة المتغير الأول قريبة من ~ 1.8 ، والثاني إلى ~ 32. هذه القيم (1.8 و 32) هي قيم مباشرة في صيغة تحويل الدرجات المئوية إلى فهرنهايت.

هذا هو حقا قريبة جدا من القيم الفعلية في الصيغة! سننظر في هذه النقطة بمزيد من التفصيل في مقاطع الفيديو اللاحقة ، حيث نعرض كيفية عمل الطبقة Dense ، لكن في الوقت الحالي تحتاج فقط إلى معرفة أن إحدى الخلايا العصبية ذات المدخلات والمخرجات الفردية تحتوي على رياضيات بسيطة - y = mx + b (كمعادلة مباشرة) ، والتي ليست أكثر من f = 1.8c + 32 لتحويل الدرجات المئوية إلى فهرنهايت ، f = 1.8c + 32 .

نظرًا لأن التمثيلات متشابهة ، يجب أن تتقارب قيم المتغيرات الداخلية للنموذج مع القيم المعروضة في الصيغة الفعلية ، والتي حدثت في النهاية.

مع وجود الخلايا العصبية الإضافية ، وقيم المدخلات الإضافية وقيم المخرجات ، تصبح الصيغة أكثر تعقيدًا قليلاً ، لكن جوهرها يبقى كما هو.

قليلا من التجريب

للمتعة! ماذا يحدث إذا قمنا بإنشاء المزيد من الطبقات Dense مع مزيد من الخلايا العصبية ، والتي بدورها سوف تحتوي على المزيد من المتغيرات الداخلية؟

 l0 = tf.keras.layers.Dense(units=4, input_shape=[1]) l1 = tf.keras.layers.Dense(units=4) l2 = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([l0, l1, l2]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") print(model.predict([100.0])) print(" ,  100    {}  ".format(model.predict([100.0]))) print("    l0: {}".format(l0.get_weights())) print("    l1: {}".format(l1.get_weights())) print("    l2: {}".format(l2.get_weights())) 

الاستنتاج:

    [[211.74748]]  ,  100    [[211.74748]]       l0: [array([[-0.5972079 , -0.05531882, -0.00833384, -0.10636603]], dtype=float32), array([-3.0981746, -1.8776944, 2.4708805, -2.9092448], dtype=float32)]     l1: [array([[ 0.09127654, 1.1659832 , -0.61909443, 0.3422218 ], [-0.7377194 , 0.20082018, -0.47870865, 0.30302727], [-0.1370897 , -0.0667181 , -0.39285263, -1.1399261 ], [-0.1576551 , 1.1161333 , -0.15552482, 0.39256814]], dtype=float32), array([-0.94946504, -2.9903848 , 2.9848468 , -2.9061244 ], dtype=float32)]     l2: [array([[-0.13567649], [-1.4634581 ], [ 0.68370366], [-1.2069695 ]], dtype=float32), array([2.9170544], dtype=float32)] 

كما قد تلاحظ ، فإن النموذج الحالي قادر أيضًا على التنبؤ جيدًا بالدرجات المقابلة من فهرنهايت. ومع ذلك ، إذا نظرنا إلى قيم المتغيرات الداخلية (الأوزان) من الخلايا العصبية حسب الطبقات ، فلن نرى أي قيم مماثلة ل 1.8 و 32. يخفي التعقيد الإضافي للنموذج الشكل "البسيط" لتحويل الدرجات المئوية إلى فهرنهايت.

ابق على اتصال وفي الجزء التالي ، سننظر في كيفية عمل الطبقات الكثيفة "تحت الغطاء".

ملخص موجز

تهانينا! لقد قمت للتو بتدريب النموذج الأول الخاص بك. في الممارسة العملية ، رأينا كيف ، من خلال قيم المدخلات والمخرجات ، تعلم النموذج ضرب قيمة الإدخال بمقدار 1.8 وإضافة 32 إليها للحصول على النتيجة الصحيحة.



كان هذا مثيرًا للإعجاب حقًا ، بالنظر إلى عدد سطور التعليمات البرمجية التي نحتاجها لكتابة:

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) model = tf.keras.Sequential([l0]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) model.predict([100.0]) 

المثال أعلاه هو خطة عامة لجميع برامج التعلم الآلي. سوف تستخدم إنشاءات مشابهة لإنشاء وتدريب الشبكات العصبية ولحل المشاكل اللاحقة.

عملية التدريب

تتكون عملية التدريب (التي تجري في الطريقة model.fit(...)) من تسلسل بسيط للغاية من الإجراءات ، ينبغي أن تكون النتيجة هي قيم المتغيرات الداخلية التي تعطي النتائج أقرب ما يمكن إلى الأصل. تستخدم عملية التحسين التي يتم من خلالها تحقيق هذه النتائج ، والتي تسمى تدرج النسب ، التحليل العددي لإيجاد أفضل القيم للمتغيرات الداخلية للنموذج.

من أجل الانخراط في التعلم الآلي ، أنت ، من حيث المبدأ ، لا تحتاج إلى فهم هذه التفاصيل. ولكن بالنسبة لأولئك الذين ما زالوا مهتمين بمعرفة المزيد: تغيير التدرج اللوني من خلال التكرار يغير قيم المعلمة قليلاً ، "يجذبهم" في الاتجاه الصحيح حتى يتم الحصول على أفضل النتائج. في هذه الحالة ، تعني "أفضل النتائج" (أفضل القيم) أن أي تغيير لاحق في المعلمة لن يؤدي إلا إلى تفاقم نتيجة النموذج. تسمى الوظيفة التي تقيس مدى جودة أو سوء النموذج في كل تكرار "وظيفة الخسارة" ، والهدف من كل "سحب" (تعديل القيم الداخلية) هو تقليل قيمة وظيفة الخسارة.

تبدأ عملية التدريب بكتلة "التوزيع المباشر" ، حيث تنتقل معلمات الإدخال إلى إدخال الشبكة العصبية ، وتتبع الخلايا العصبية المخفية ، ثم تذهب إلى عطلة نهاية الأسبوع. ثم يطبق النموذج التحويلات الداخلية على قيم المدخلات والمتغيرات الداخلية للتنبؤ بالاستجابة.

في مثالنا ، تكون قيمة المدخلات هي درجة الحرارة بالدرجات المئوية وتوقع النموذج القيمة المقابلة بالدرجات فهرنهايت.



بمجرد توقع القيمة ، يتم حساب الفرق بين القيمة المتوقعة والقيمة الصحيحة. يسمى الفرق "الخسارة" وهو شكل من أشكال قياس مدى نجاح النموذج. يتم حساب قيمة الخسارة بواسطة دالة الخسارة ، والتي حددناها بواسطة إحدى الوسيطات عند استدعاء الطريقة model.compile(...).

بعد حساب قيمة الخسارة ، يتم ضبط المتغيرات الداخلية (الأوزان والتشريد) لجميع طبقات الشبكة العصبية لتقليل قيمة الخسارة من أجل تقريب قيمة الخرج إلى القيمة المرجعية الأولية الصحيحة.



تسمى عملية التحسين هذه بانحدار التدرج . يتم استخدام خوارزمية تحسين محددة لحساب قيمة جديدة لكل متغير داخلي عند استدعاء الطريقة model.compile(...). في المثال أعلاه ، استخدمنا خوارزمية التحسين Adam.

إن فهم مبادئ العملية التدريبية غير مطلوب في هذه الدورة ، ولكن إذا كنت فضوليًا بما يكفي ، يمكنك العثور على مزيد من المعلومات في دورة تحطم Google(وترد الترجمة والجزء العملي من الدورة بأكملها في خطط المؤلف للنشر).

في هذه المرحلة ، يجب أن تكون على دراية بالشروط التالية:

• الملكية : قيمة إدخال نموذجنا.
• أمثلة : أزواج المدخلات + الإخراج ؛
• العلامات : نموذج قيم الانتاج ؛
• الطبقات : مجموعة من العقد المرتبطة ببعضها داخل شبكة عصبية ؛
• نموذج : تمثيل شبكتك العصبية ؛
• كثيفة ومتصلة تمامًا : كل ​​عقدة في طبقة واحدة متصلة بكل عقدة من الطبقة السابقة.
• الأوزان والإزاحة : نموذج المتغيرات الداخلية ؛
• الخسارة : الفرق بين قيمة المخرجات المرغوبة وقيمة المخرجات الفعلية للنموذج ؛
• MSE : , , , .
• : , - ;
• : ;
• : «» ;
• : ;
• : ;
• : ;
• الانتشار الخلفي : حساب قيم المتغيرات الداخلية وفقًا لخوارزمية تحسين تبدأ من طبقة الإخراج ونحو طبقة الإدخال عبر جميع الطبقات الوسيطة.

طبقات بمعنى

في الجزء السابق ، أنشأنا نموذجًا يحول الدرجات المئوية إلى فهرنهايت باستخدام شبكة عصبية بسيطة لإيجاد العلاقة بين الدرجات المئوية ودرجات فهرنهايت.

تتكون شبكتنا من طبقة واحدة متصلة بالكامل. ولكن ما هي طبقة متصلة بالكامل؟ لمعرفة ذلك ، فلنقم بإنشاء شبكة عصبية أكثر تعقيدًا تحتوي على 3 معلمات إدخال ، وطبقة مخفية واحدة بها عصبونان وطبقة إخراج واحدة بخلية عصبية واحدة.



تذكر أنه يمكن تخيل شبكة عصبية كمجموعة من الطبقات ، كل منها يتكون من عقد تسمى الخلايا العصبية. يمكن توصيل الخلايا العصبية في كل مستوى بالخلايا العصبية لكل طبقة لاحقة. يُطلق على نوع الطبقات التي ترتبط فيها كل خلية عصبية من طبقة واحدة بكل خلية عصبية أخرى من الطبقة التالية طبقة مترابطة بالكامل (متصلة بالكامل) أو طبقة كثيفة ( Denseطبقة).



وبالتالي ، عندما نستخدم طبقات متصلة بالكامل keras، فإننا نعلم أن الخلايا العصبية لهذه الطبقة يجب أن تكون مرتبطة بجميع الخلايا العصبية في الطبقة السابقة.

لإنشاء الشبكة العصبية أعلاه ، فإن التعبيرات التالية كافية بالنسبة لنا:

 hidden = tf.keras.layers.Dense(units=2, input_shape=[3]) output = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([hidden, output]) 

, , . ?

, , « » .



, — 1, 2, 3 , 1, 2 3 — . , ? , w* b* , . إن قيم هذه المتغيرات هي التي يتم ضبطها في عملية التعلم للحصول على أكثر النتائج دقة لمقارنة قيم المدخلات بالمخرجات.



ما يجب أن تضعه في الاعتبار بالتأكيد هو أن الرياضيات الداخلية للخلايا العصبية تبقى كما هي . بمعنى آخر ، أثناء عملية التدريب ، لا تتغير إلا الأوزان والتهجير.

عندما تبدأ في تعلم التعلم الآلي ، قد يبدو غريباً - حقيقة أنه يعمل حقًا ، ولكن هذه هي الطريقة التي يعمل بها التعلم الآلي!

دعنا نعود إلى مثالنا لتحويل درجات مئوية إلى درجة فهرنهايت.



مع خلية عصبية واحدة ، لدينا وزن واحد ونزوح واحد فقط. هل تعرف ماذا؟ هذا هو بالضبط ما تبدو عليه صيغة تحويل الدرجات المئوية إلى درجة فهرنهايت. إذا استبدلنا w11القيمة 1.8، وبدلاً من b1- 32، سنحصل على نموذج التحول النهائي!

إذا عدنا إلى نتائج نموذجنا من الجزء العملي ، فإننا نلاحظ حقيقة أن مؤشرات الوزن والتشريد "تمت معايرتها" بطريقة تتوافق تقريبًا مع قيم الصيغة.

لقد أنشأنا عمدا مثل هذا المثال العملي من أجل إظهار المقارنة الدقيقة بين الأوزان والإزاحات بوضوح. بوضع التعلم الآلي موضع التطبيق ، لا يمكننا أبدًا مقارنة قيم المتغيرات مع الخوارزمية المستهدفة بهذه الطريقة ، كما في المثال أعلاه. كيف يمكننا أن نفعل هذا؟ بأي حال من الأحوال ، لأننا لا نعرف حتى الخوارزمية المستهدفة!

لحل مشاكل التعلم الآلي ، نقوم باختبار العديد من بنى الشبكات العصبية بأعداد مختلفة من الخلايا العصبية فيها - عن طريق التجربة والخطأ نجد أدق البنى والنماذج ونأمل أن يحلوا المشكلة في عملية التعلم. في الجزء العملي التالي ، سنكون قادرين على دراسة أمثلة محددة لهذا النهج.

ابق على اتصال ، لأنه الآن تبدأ المتعة!

النتائج

في هذا الدرس ، تعلمنا الأساليب الأساسية في التعلم الآلي وتعلمنا كيفية عمل الطبقات (الطبقات) المتصلة بالكامل Dense. قمت بتدريب النموذج الأول الخاص بك لتحويل درجة مئوية إلى درجة فهرنهايت. لقد تعلمت أيضًا المصطلحات الأساسية المستخدمة في التعلم الآلي ، مثل الخصائص والأمثلة والعلامات. أنت ، من بين أشياء أخرى ، كتبت الأسطر الرئيسية للشفرة في بيثون ، والتي هي العمود الفقري لأي خوارزمية للتعلم الآلي. لقد رأيت أنه في بضعة سطور من التعليمات البرمجية يمكنك إنشاء وتدريب وطلب التنبؤ من شبكة عصبية باستخدام TensorFlowو Keras.

... ومكالمة تحث على اتخاذ إجراء - اشترك ، ضع علامة زائد وشاركه :)


YouTube: https://youtube.com/channel/ashmig
Telegram: https://t.me/ashmig
VK: https://vk.com/ashmig