حول بحث العمليات غير الثابتة

من المعروف أن معظم السلاسل الزمنية التي يتعين على الباحث التعامل معها غير ثابتة ، وتحليلها أكثر تعقيدًا بكثير من دراسة العمليات الثابتة. نظرًا لأنه يبدو أن الاهتمام بالموجات اللاسلكية قد تراجع ، فمن المفيد مناقشة بعض الأدوات "غير الثابتة" الأخرى ، والتي تعد مناسبة بشكل أساسي لتقدير الترددات الفورية ، وكذلك لتقييم الأطياف اللحظية.

بادئ ذي بدء ، من المنطقي أن نتذكر "الإشارة التحليلية". أدناه ، يشير "An-model" إلى المعاوقة الفورية وقوة إشارة الاختبار بعد الانتهاء من الجزء التخيلي (تحول في الطور بمقدار π / 2).

لكن ليس من الممكن دائمًا العبث بتحول جيلبرت. في وقت سابق ، سبق ذكر طريقة تقدير الطيف الانحداري المناسبة للعمل مع تسلسلات قصيرة. هنا ، سيتم فهم "AR-model" على أنه دراسة شظايا قصيرة (من 5 عينات) متداخلة من الإشارة الأصلية من أجل تحديد معاملات الانتهاك الذاتي من الدرجة الثانية ، والعثور على "أعمدة" النموذج منها ، إلخ.




تعتمد كلتا الطريقتين الموصوفتين هنا على مبدأ واحد - الافتراض بأنه في حي صغير من لحظة الوقت المحددة ، يمكن تقريب العملية قيد الدراسة بتسلسل "أسي" - مجمع واحد (An) أو مجموع مجموعتين من الأسس المترافق المعقدة (AR).

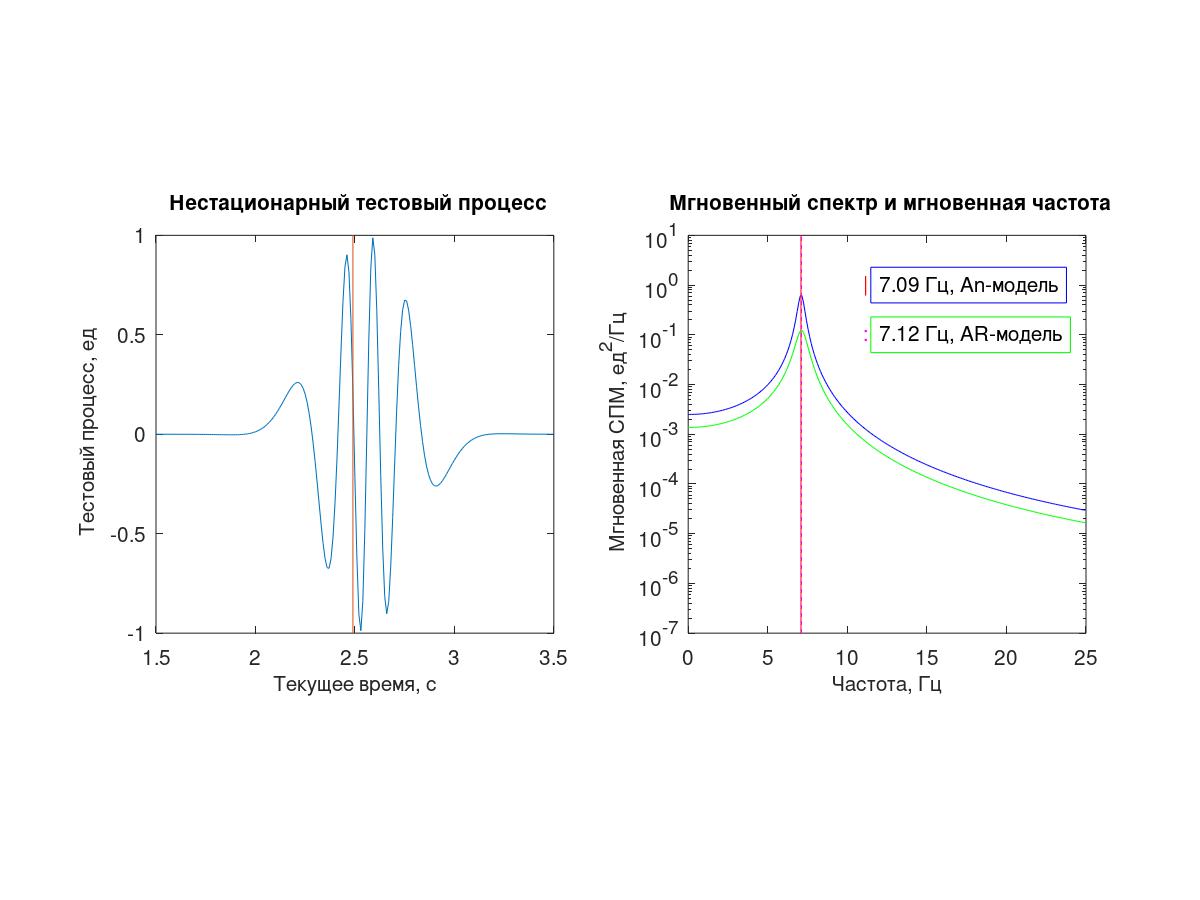
كعملية اختبار ، تم استخدام سلسلة من 512 عينة مع فاصل أخذ عينات مشروط 0.01t = 0.01 s تم الحصول عليها من عملية حتمية مستمرة (1).



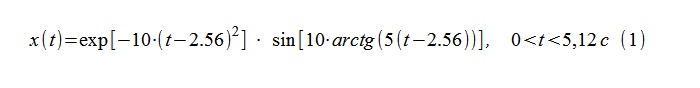
من خلال "اللوغاريتم" والتمييز اللاحق للملء عالي التردد والمغلف ، على التوالي ، من (1) ، يتم الحصول على التعبيرات النظرية للتردد (الفوري) وتناقص (2)



بالنسبة للنمذجة باستخدام طريقة الرسم البياني (تحويل فورييه المباشر والعكسي) ، يتم إنشاء إشارة تحليلية y [i] من التسلسل الأولي x [i].



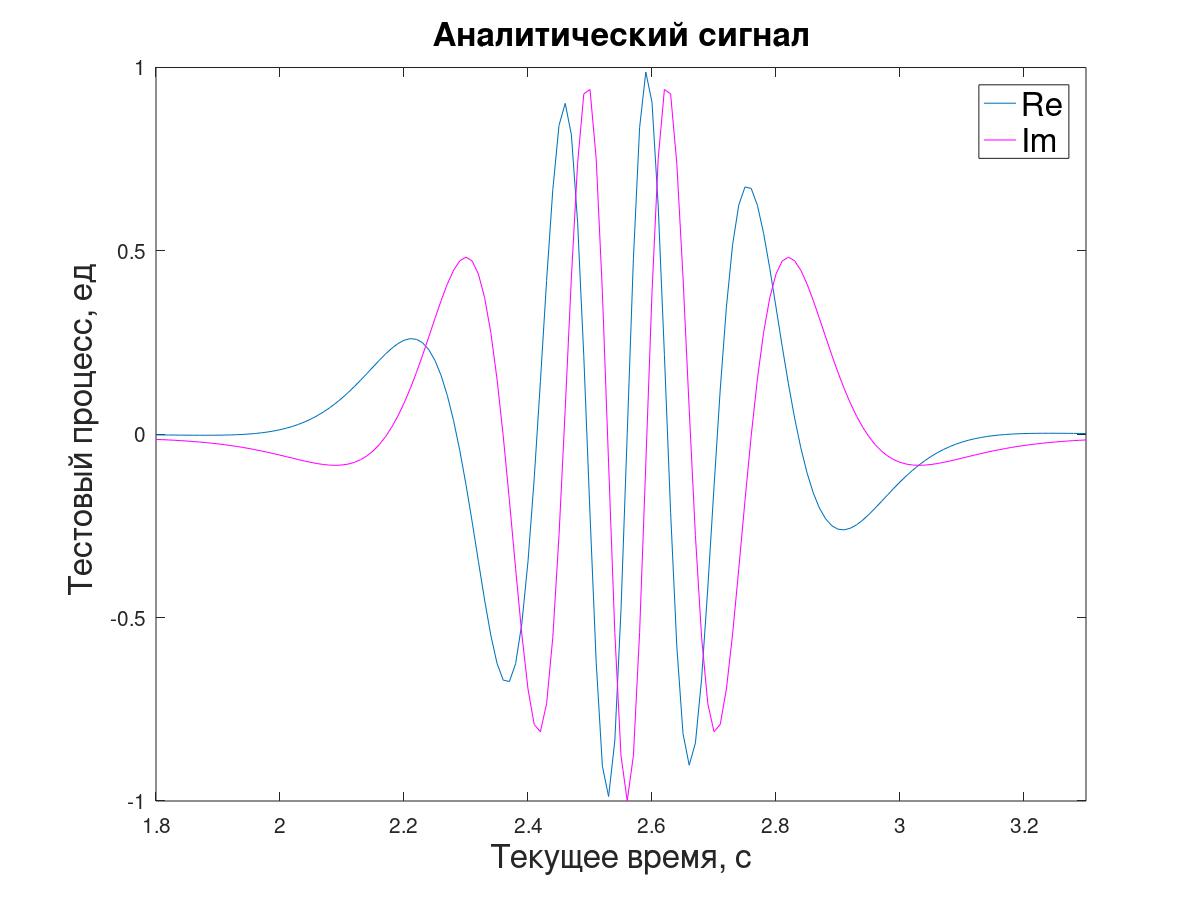
تسمح لك نسبة عينتين متتاليتين لهذه الإشارة ، من حيث المبدأ ، بتحديد المعاوقة اللحظية but ، ولكن من أجل تبسيط هذه المهمة التوضيحية - حتى لا تهتم بإنشاء نماذج وسيطة أو شرح تحول التقدير بواسطة Δt / 2 - تقرر العمل مع عينات "من خلال واحدة" ، وحساب λ _i فيما يتعلق بقيم إشارة y [i + 1] اللاحقة إلى y السابقة [i-1] (3).



بالنسبة لنمذجة AR (نموذج من الدرجة الثانية) ، تم استخدام الإجراء القياسي لحساب معاملات الارتباط التلقائي 1 ، و 1 i ، و _{2 i} باستخدام معادلات Yule-Walker ، وتم استخدام تسلسلات 5 عينات x [i-2] و x [i -1] ، ... × [i + 2] (4).



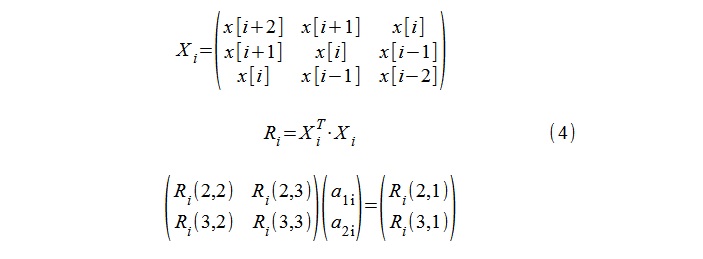
ثم _يتم حساب "أقطاب" النموذج easily _i بسهولة باستخدام لوغاريتم جذور المعادلة التربيعية (5).





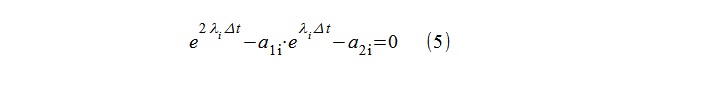
بناء التقديرات الطيفية من "الأقطاب" المعروفة إلى عامل القياس ليس بالأمر الصعب . التالي. من الواضح أن "القدرة اللحظية" للنموذج An تعرف بأنها | y [i] | ² ، ومسألة تحجيم هذا التقدير ويبدو أن تسوية. بالنسبة لنموذج AR ، فإن الأسلوب المعتاد المرتبط بتحديد قوة الضوضاء البيضاء التقليدية ، في حالة وجود إشارة غير مستقرة ، "لا يعمل". لعدم وجود أفضل الأفكار ، تم تطبيق التحجيم على أساس مربع متوسط ​​العينات 5 المقابلة. يبدو أنه لا يمكن فعل شيء أكثر من خلال تحليل تسلسل 5 عينات فقط. تظهر الرسوم المتحركة كيف "يفشل" مخطط SPM AR بشكل ملحوظ في بعض الأحيان بالنسبة إلى درجة An. يجب أن يكون من المفهوم أن لحظات الانتقال من "خلال الصفر" لنموذج AR يمكن أن تكون صعبة ليس فقط من حيث الأخطاء مع التردد الفوري ، ولكن أيضًا مع السعة الآنية ، خاصة في منطقة التردد المنخفض.

بعض التعليقات في النهاية.

1. من التجربة ، عادة ما تعطي كلتا الطريقتين نتائج جيدة في تقدير التردد الفوري ، على الأقل في متوسط ​​نطاق التردد (على أساس تردد أخذ العينات).
2. إن الجودة العالية نسبياً لنتائج An-method وبساطتها وسهولة فهمها وتنفيذها هي أكثر من "تعويض" بالصعوبات المحتملة في تحويل العملية وفقًا لجيلبرت. يمكن أن يكون للمرشح الرقمي Gilbert من النوعية الجيدة ، خاصة في نطاق الترددات العريض ، ترتيبًا عاليًا بشكل غير مقبول. عند تنفيذ طريقة زمنية بديلة لهذا التحول ، يجب أن يؤخذ في الاعتبار أن تحويل فورييه يتضمن ضمنيًا إكمال العملية إلى دورية. نتيجة لذلك ، قد تكون هناك حاجة إلى إكمال كبير للعملية مع الأصفار. يتم تفسير الجودة العالية لنتائج An-method من خلال استخدامها للمعلومات في حي شاسع للغاية من الوقت المحدد المحدد (بالمعنى الدقيق للكلمة - حول التنفيذ المؤقت الكامل للعملية) ، وهذه الخاصية نفسها تجعل من الصعب تنفيذ الطريقة (على سبيل المثال ، عند العمل في الوقت الفعلي).
3. إذا لزم الأمر ، يمكن التوصية بالتدابير التالية لتحسين نتائج طريقة AR:
   
   • ترقق البيانات (بمعدل أخذ العينات مرتفع للغاية)
   • زيادة في عدد المتوسطات - امتدادًا لـ "لحظة الوقت" المتضمنة في نموذج الحي - بناء مصفوفة المسار X مع عدد كبير من الصفوف.
   • زيادة ترتيب نموذج AR.