وجدت أدلة على أن جميع التغييرات هي مزيج من النظام والفرصة

جميع أوصاف التغييرات هي مزيج فريد من الصدفة والحتمية ، وفقًا للإثبات الجذري لـ "فرضية Pinsker الضعيفة"

تخيل حديقة حيث تنمو كل أزهار العالم - بساتين الفاكهة الرقيقة ، عباد الشمس الشاهقة ، زهور الشمع في صبار كارنيجي والنورات النتنة للمورقة العملاقة . الآن تخيل أن كل هذا التنوع النباتي قد وصل إلى خيارين فقط ، وأنه من خلال عبورهما ، يمكنك إنتاج كل الخيارات الأخرى.

هذه هي طبيعة أحد أكثر الأدلة جذرية التي تم الحصول عليها في السنوات الأخيرة. صممه تيم أوستن ، عالم رياضيات من جامعة كاليفورنيا في لوس أنجلوس. ولكن بدلاً من الزهور ، يرتبط عمل أوستن بأحد أكثر الأشياء دراسة في الرياضيات: وصف رياضي للتغييرات.

تنطبق هذه الأوصاف ، المعروفة باسم الأنظمة الديناميكية ، على كل شيء بدءًا من تحركات الكواكب إلى تقلبات سوق الأسهم. أينما ينشأ نظام ديناميكي ، يريد علماء الرياضيات فهم أساسياته. وإحدى الحقائق الأساسية هي أن أي نظام ديناميكي معقد بشكل تعسفي يمكن تقسيمه إلى عناصر عشوائية وحتمية.

هذا السؤال هو موضوع "فرضية Pinsker الضعيفة" ، التي صيغت لأول مرة في السبعينيات. يقدم دليل الفرضية الذي قدمته أوستن طريقة بديهية وأنيقة للتفكير في كل أنواع الظواهر الغامضة. لقد أظهر أنه ، في جوهره ، كل من هذه الأنظمة الديناميكية هي مزيج من الصدفة والحتمية.

مصير وفرصة

يبدأ النظام الديناميكي ببعض بيانات الإدخال ، على سبيل المثال ، مع وضع البندول ، ويطبق قواعد معينة ، على سبيل المثال ، قوانين نيوتن للحركة ، ويؤدي إلى نتيجة معينة ، على سبيل المثال ، موضع البندول في ثانية واحدة. الأهم من ذلك ، تسمح لك الأنظمة الديناميكية بتكرار هذه العملية: يمكنك أن تأخذ موقعًا جديدًا في البندول ، وتطبق القواعد نفسها ، وتضع موضعها في ثانية أخرى.

الأنظمة الديناميكية هي أيضًا رياضية بحتة. يمكنك تحديد رقم البداية ، وتطبيق قاعدة "ضرب الرقم في اثنين" والحصول على رقم جديد. يتيح لك هذا النظام أيضًا إدخال العدد الإجمالي مرة أخرى في معالج القواعد والحصول على المزيد من الأرقام.

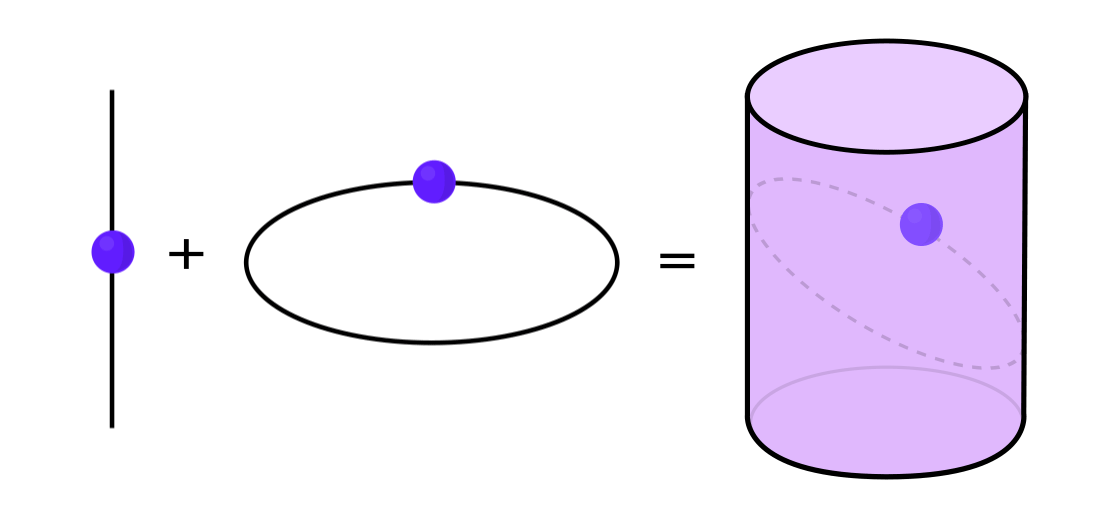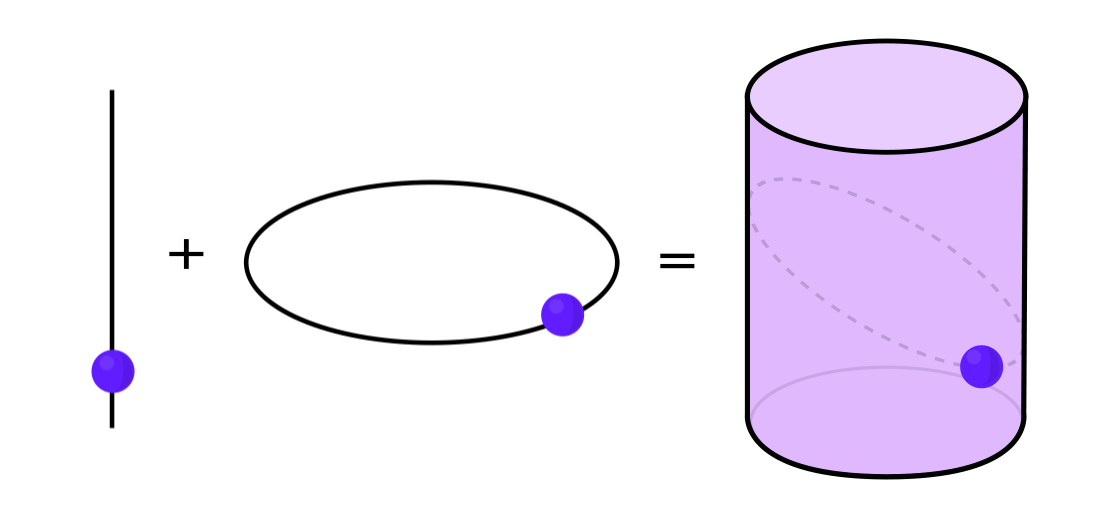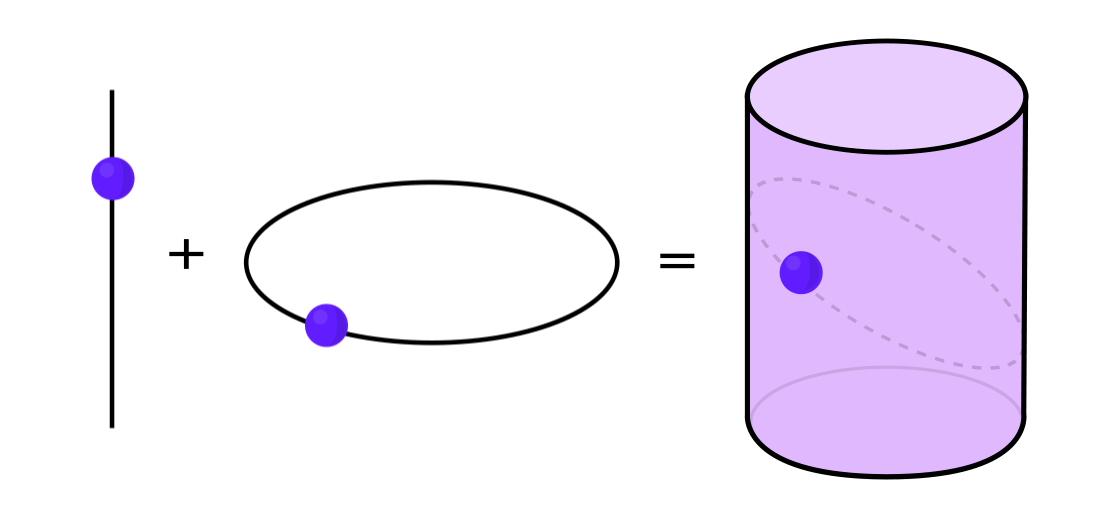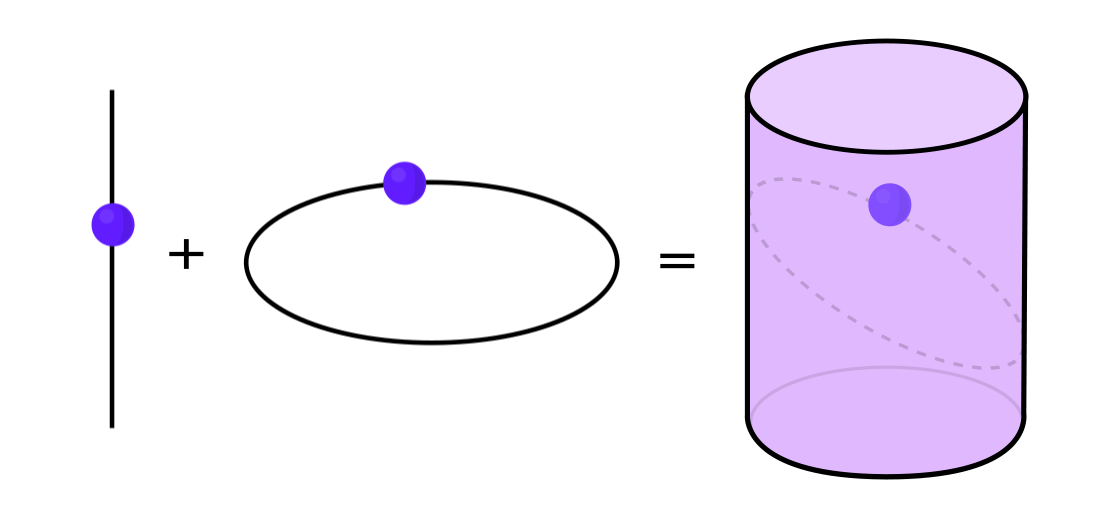
يمكن التعبير عن أنواع معينة من الأنظمة الديناميكية كمزيج من نظامين ديناميين أبسط. يعمل هذان النظامان بشكل مستقل عن بعضهما البعض ، ولكن يمكن دمجهما لتشكيل نظام أكثر تعقيدًا. على سبيل المثال ، تخيل وجود نظام ديناميكي يحرك نقطة على سطح الأسطوانة. يمكنك إدخال موضع النقطة ، وتطبيق القواعد ، والحصول على نقطة أخرى.

يمكن تفكيك هذا النظام إلى قسمين بسيطين. الأول هو نظام ديناميكي يحرك نقطة حول دائرة. والثاني هو النظام الذي يحرك نقطة أعلى وأسفل عموديا. من خلال الجمع بين نظامين - الحركة الدائرية والحركة المستقيمة - نحصل على حركة نقطة أكثر تعقيدًا على طول الاسطوانة.



وقالت كاثرين ليندساي ، عالمة رياضيات في كلية بوسطن: "بدلاً من دراسة النظام الديناميكي بأكمله ، تحتاج إلى تقسيمه إلى أجزاء ، أجزاء صغيرة من المنطقي أن تدرسها".

هناك نوعان من المرشحين الطبيعيين لدور هذه اللبنات الأساسية. السابق أنظمة ديناميكية حتمية بالكامل ، مثل مثال البندول الخاص بنا. إذا كنت تعرف موضع البندول في وقت ما ، فيمكنك التنبؤ به في أي وقت في المستقبل.


جان بول توفينو في عام 1975 ، قبل عامين من صياغة فرضية Pinsker الضعيفة

النوع الثاني من الأنظمة الديناميكية عشوائي تمامًا. على سبيل المثال ، تخيل نظامًا ديناميكيًا بهذه القاعدة: إرم عملة معدنية. إذا كان هناك نسر ، خذ خطوة إلى اليسار ؛ إذا الذيول ، أليس كذلك. سيكون المسار النهائي عشوائيًا تمامًا ، أي أنه حتى لو كنت تعرف كل شيء عن المسار السابق ، فإن هذه المعلومات لن تساعدك على التنبؤ بالخطوة التالية.

بعض الأنظمة الديناميكية عشوائية تمامًا ، وبعضها الآخر حاسم تمامًا ، ومعظمها في مكان ما - فهي مزيج من الاثنين. على سبيل المثال ، تخيل نسخة معدلة قليلاً من سيرنا العشوائي. نسير على طول طريق مزروع بالورود ، وألوانها عشوائية أيضًا. تبقى القاعدة كما هي: إذا سقط النسر ، فاذهب لليسار ؛ إذا الذيول ، أليس كذلك. ماذا سيكون تسلسل ألوان الزهور؟

أولا أقول عشوائي. بعد كل شيء ، تم اختيار الألوان نفسها بشكل عشوائي ، وحركتك هي أيضا عشوائية. ومع ذلك ، بعد أن تخطيت زهرة واحدة ، يزداد احتمال أن تمر بها في المستقبل ، وذلك ببساطة لأنك لست بعيدًا عنها. تسلسل ألوان الزهور لن يكون عشوائيًا تمامًا.

وقال أوستن: "إذا وقفت بجانب الأحمر ، فإن ذلك يزيد من فرص أن تقابل الأحمر في خطوتين مرة أخرى ، لأنه قد يحدث أن تخطو إلى اليسار ، ثم إلى اليمين ، وتعود إلى نفس المكان".

ينتج عن مثل هذا "السير العشوائي عبر منظر طبيعي عشوائي" إخراج - سلسلة من الألوان - عشوائي جزئيًا ولا جزئيًا. في عام 1960 ، اقترح عالم الرياضيات مارك بينسكر أن فئة كبيرة معينة من الأنظمة الديناميكية لها الخاصية التالية: فهي مزيج من نظام ديناميكي عشوائي مع نظام حتمية.

ينطبق تخمين Pinsker على فئة الأنظمة الديناميكية التي لها خاصية مشتركة مهمة. النقاط الموجودة فيها لا تبتعد عن بعضها البعض ولا تتقلص أثناء تطوير النظام. بتعبير أدق ، إذا قمت برسم حلقة حول مجموعة من النقاط في مساحتك (قد تكون المساحة مثل سطح الأسطوانة) ، ابدأ في تطوير نظام ديناميكي لفترة طويلة من الزمن ، ثم ارسم حلقة حول مجموعة النقاط الناتجة ، ثم المنطقة التي تشير إليها النقاط نهاية ، يتزامن مع المنطقة التي احتلوها في البداية. وتسمى هذه النظم "تدبير المحافظة"

وقال عساف ناعور ، عالم الرياضيات في جامعة برينستون: "إذا كانت فرضية بنسكر الأصلية صحيحة ، فسيكون ذلك وصفًا رائعًا للعالم". ولكن Pinsker كان خطأ. في عام 1973 ، دحض دونالد أورنشتاين فرضيته. وقالت برينا كرا ، عالمة رياضيات في جامعة نورث وسترن "كانت الصياغة طموحة للغاية".

في الرياضيات ، يحدث غالبًا أنه بعد دحض الفرضية العامة ، يحاول علماء الرياضيات صياغة نسخة أكثر تواضعًا منها. في عام 1977 ، اقترح عالم الرياضيات جان بول توفينو فرضية Pinsker الضعيفة. لقد خفف الصياغة الأصلية ، مشيرًا إلى أن الأنظمة الديناميكية التي كان يفكر فيها Pinsker كانت نتيجة للجمع بين نظام عشوائي بحت مع نظام حتمي تمامًا تقريبًا.

يميز "الصقل" تقريبًا فرضية توفينو عن فرضية بينسكر. لقد كان يعني أنه يجب أن يكون لنظام الحتمية البسيط بعض أثر الصدفة. قد يكون هذا التتبع صغيرًا ، لكن يجب أن يكون هناك. وقال توفينو إن فكرة بنسكر ستنجح بينما هو كذلك.

وقال ناور: "لقد كان قريبًا من الفرضية الأصلية ، وأظهر توفينو أنه إذا كان الأمر كذلك ، فستتضمن الفرضية عددًا كبيرًا من التطبيقات الممتازة".

في العقود التالية ، لم يحقق علماء الرياضيات نجاحًا كبيرًا في إثبات فرضية Pinsker الضعيفة. قلة التقدم جعلت توفينو يعتقد أنه حتى صيغته الضعيفة ستكون خاطئة. وقال "في مرحلة ما ، اعتقدت أن كل شيء سيكون عكس ذلك ، وأنه لن يكون عالميًا".

ثم ظهر تيم أوستن.

حل الخطوة

لإثبات فرضية Pinsker الضعيفة ، كان من الضروري إيجاد طريقة دقيقة للتدقيق في نظام ديناميكي - نظام يسمح له بفصل أجزائه العشوائية والحتمية تقريبًا. لقد أثبت العمل السابق أنه سيكون من الأصعب عزل العناصر مع القليل من العشوائية.

وقال توفينو: "من الصعب للغاية اكتشاف العوامل العشوائية الصغيرة ، والجزء المركزي من الأدلة هو إيجاد طريقة لاكتشاف بنية عشوائية صغيرة".


تيم أوستن ، عالم رياضيات في جامعة كاليفورنيا ، لوس أنجلوس

تمكن أوستن من التعامل مع العناصر العشوائية الصغيرة لنظام ديناميكي من خلال تغيير وجهات النظر. تعمل الأنظمة الديناميكية على مساحة مستمرة ، مثل نقطة تتحرك على طول سطح الأسطوانة ، أو يتأرجح البندول في الفضاء. في هذه المساحات ، تتحرك النقاط على طول الأقواس المستمرة وفقًا لقواعد النظام الديناميكي. تعمل هذه الأنظمة أيضًا على عدد لا حصر له من الخطوات - يمكن أن تعمل إلى الأبد.

ولكن في برهانه ، تخلى أوستن عن الفضاء الأملس المستمر ونسي العمل الأبدي للأنظمة الديناميكية. بدلاً من ذلك ، بدأ في تحليل ما يمكن أن يحدث إذا سُمح لهم بالعمل مرات منفصلة ، مثل مليون خطوة. وهكذا طبق الطريقة التي ابتكرها توفينو.

وقال أوستن "إن المساهمة الرئيسية لتوفينو كانت أنه أدرك أنه إذا كنت تقوم بالخطوات الرياضية الصحيحة بخطوط طويلة محدودة ، فيمكنك إثبات خصائص النظام الديناميكي". "كان إسهامي الرئيسي هو أنني أثبتت ما هو مطلوب للخطوط الطويلة".

يتخيل أوستن نظامًا ديناميكيًا يصدر سلسلة من الأصفار والأصفار. إذا كان النظام الديناميكي يرمي عملة معدنية ، فمن السهل أن نتخيلها: ستكون ذيول 1 والرؤوس ستكون 0. ولكن يمكن استخدام أي نظام ديناميكي لتوليد تسلسل ثنائي عن طريق تقسيم المساحة التي تعمل فيها إلى اثنين (ليس بالضرورة مساوياً) جزء.



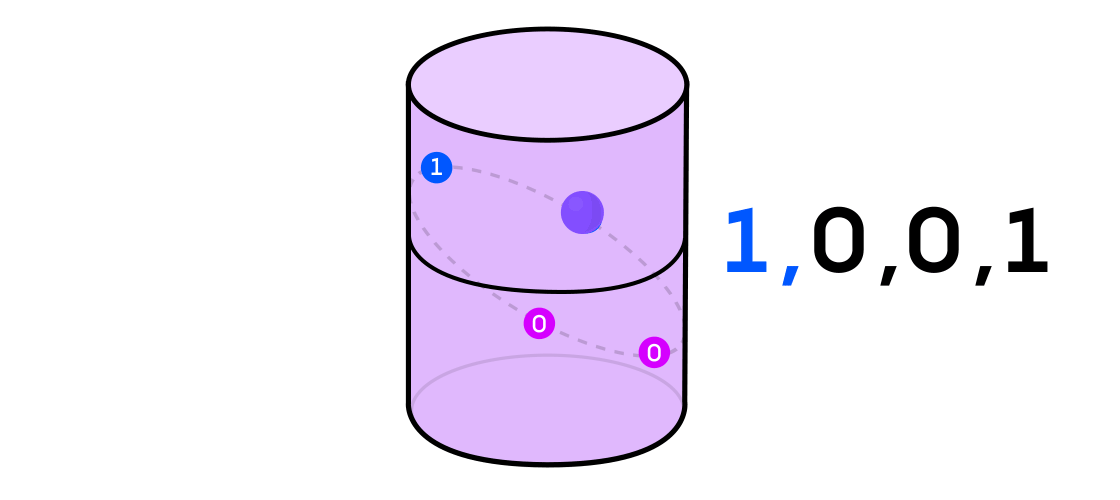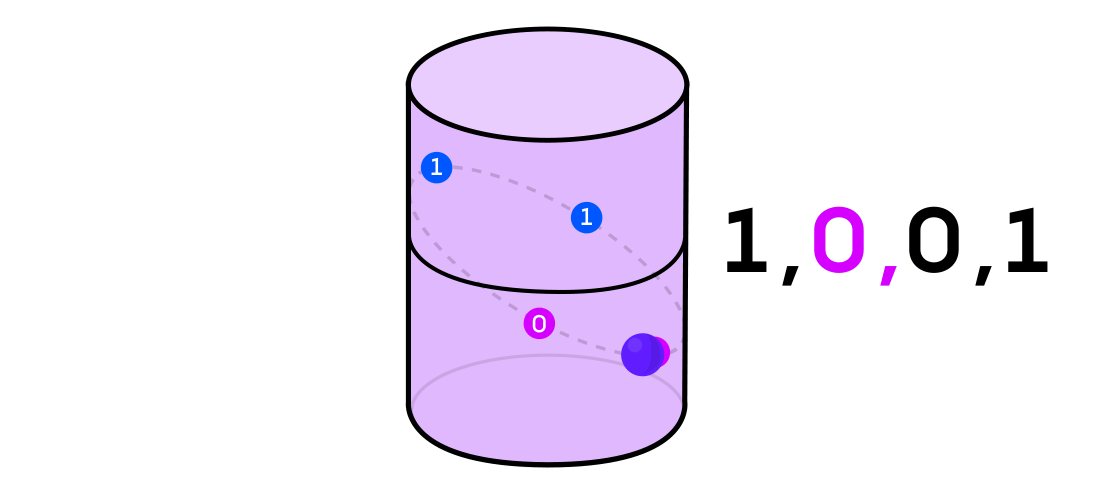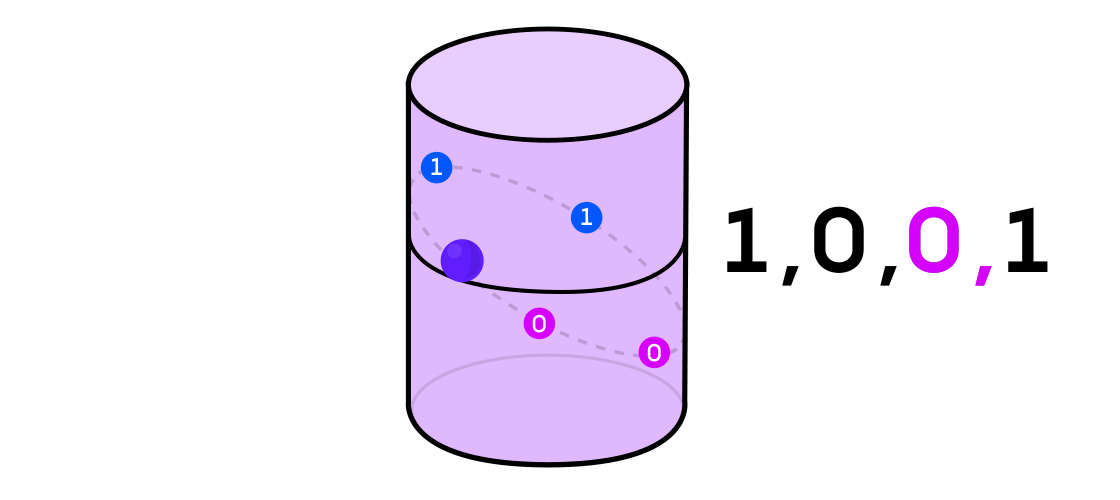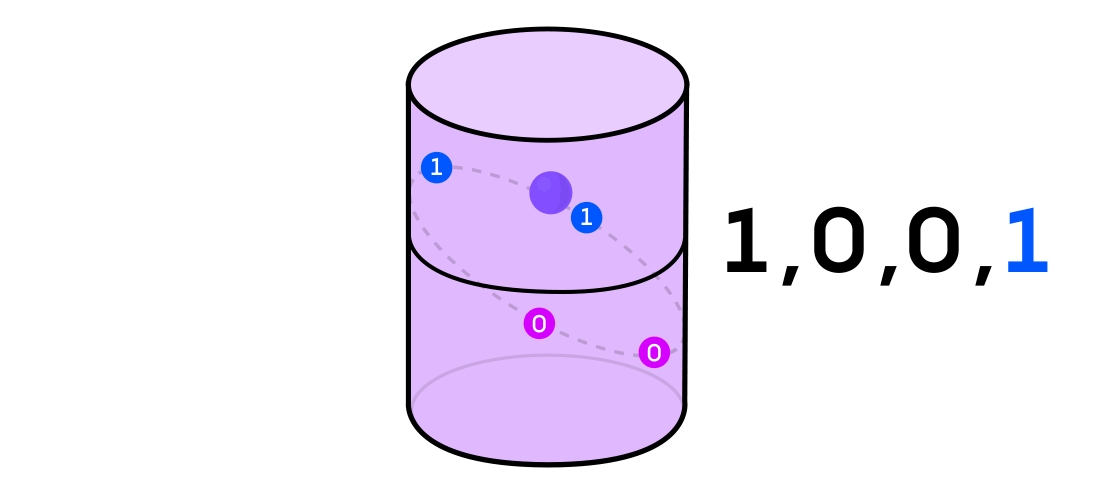
بالرجوع إلى مثال النظام الديناميكي على أسطوانة ، إذا كانت النقطة في جزء من الأسطوانة ، فإنك تشير إلى قيمة إخراج النظام 1 ، وإذا كانت على الجانب الآخر ، ثم 0.

حلل أوستن هذه التسلسلات الثنائية باستخدام أداة نظرية المعلومات تسمى مكعبات هامينغ . تخيل مكعبًا من القمم متصل بحواف. يتم تعيين الأرقام الثنائية لكل رأس - على سبيل المثال ، 001 أو 101. في كل مرة ، عند التبديل من رأس إلى آخر ، يتغير أحد الأرقام الثلاثة.

يمكن أن تكون مكعبات Hamming أكثر تعقيدًا منا ، حيث يمكن أن يكون لها عدد أكبر من الحواف والرؤوس بأبعاد أكثر من ثلاثة - لكن كلها لها خاصية ، بسبب المسافة بين أي من رأسين - أو عدد الحواف التي تحتاج إلى الذهاب إليها للانتقال من قمة إلى أخرى يساوي عدد الأماكن التي يتم تمييز خطوط المعلومات المقابلة لها. لذلك ، يقع 000 على مسافة حافة واحدة من 001 ، حواف من 011 وثلاثة من 111.



لعزل العناصر العشوائية والحتمية التي تشكل نظامًا ديناميكيًا معقدًا ، فكر أوستن في عدد المرات التي يمكن فيها للنظام الديناميكي إنتاج تسلسل معين من الأصفار والعناصر الممثلة في مكعب هامينغ. أثبت أنه يتم توزيع هذه التسلسلات في مكعب بطريقة معينة. تتراكم في عدد صغير من المناطق الفرعية المكعبية - وتعكس هذه المجموعة حتمية النظام - ومع ذلك ، يتم توزيعها بشكل عشوائي بين التسلسلات داخل هذه المجموعات ، مما يعكس العشوائية للنظام.

كان هذا الدوار ضروريًا لحل مشكلة لم تستسلم للهجمات المباشرة.

وقال لويس بوين ، عالم الرياضيات بجامعة تكساس في أوستن: "ما فاجأني لم يكن حقيقة أو زيف فرضية بينسكر الضعيفة ، ولكن كيف اتضح أن هذه المهمة كانت تبدو خبيثة للغاية". "قبل ظهور الأدلة ، لم يكن لدينا ، إلى حد كبير ، أي فكرة عما إذا كان يمكن القيام بذلك على الإطلاق."

تعطي نتيجة أوستن البنية الأساسية لمجموعة واسعة من الأنظمة الديناميكية. بالنسبة إلى علماء الرياضيات ، الذين يدورون في كثير من الأحيان بين أشياء تبدو مترابطة ، ليس من الواضح كيف يعطي الدليل جغرافيا محددة. الآن لديهم دليل لهذه الأنظمة الديناميكية ، على الرغم من أنه لا يزال مجهولاً ما نوع الاكتشافات التي سيؤدي إليها هذا.

"إن علماء الرياضيات يهتمون دائمًا ببنات البناء التي تشكل أي شيء" ، قالت ليندساي. "إن دليل أوستن هو نتيجة ممتازة ، من المحتمل أن يكون لها العديد من التطبيقات في الرياضيات البحتة ، لكن لا يمكنني أن أقول ما سيكون عليه."