ARA: خوارزمية لإيجاد الحد الأقصى لعدد النقاط على خط مستقيم

في الآونة الأخيرة ، واجهت مشكلة كلاسيكية للمقابلات: البحث عن أكبر عدد ممكن من النقاط التي تقف على خط مستقيم (على متن طائرة ، إحداثيات عدد صحيح). تتبادر إلى ذهني فكرة البحث الشامل ، والتي لها تعقيد زمني واضح في O (n ^ 2) ، لكن يبدو لي أنه يجب أن يكون هناك شيء آخر ، على الأقل بعض البدائل في O (n * log (n)) . بعد نصف ساعة ، تم العثور على شيء أفضل!



_{يوجد بيان أكثر تفصيلاً للمشكلة مع أمثلة المدخلات والمخرجات على GeeksForGeeks و LeetCode}

في البداية ، لاحظت أنه لا يمكنك حل المشكلة بسهولة إلا للخطوط الأفقية أو الرأسية ، مضيفًا X / Y لكل نقطة في القاموس. وما هو الفرق بين الخطوط الأخرى؟ مجرد منحدر؟ .. لكنه قابل للتثبيت!

لذلك ، قررت أنه كان من الممكن الالتفاف على قائمة النقاط بأكملها عدة مرات عن طريق تدويرها. ويتم الحصول على الحل في O (n)! على الرغم من وجود معامل كبير. آمل حقًا ألا أخترع دراجة :)

# ***  *** #   #    = 180/ROT_COUNT  # #      12, #  180*4    (6% ), #  180*20   (0% ). # ó    . #     - . ROT_COUNT = 180*10 #  #        , #       1 / MULT_COEF. #    4  . #   MULT_COEF   ROT_COUNT. # ó    - . #     - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" #   rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) #      counts = {} for pair in points: #    nx = pair[0]*co - pair[1]*si #       , #      #       #      nx = int(nx * MULT_COEF) #   if nx in counts: counts[nx] += 1 else: counts[nx] = 1 #    return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 #      for i in angles: current = mnp_rotated(points, i) #  ,     if current > res: res = current best_angle = i return res 

مرئي ، يبدو مثل هذا:
_{أول GIF محلية الصنع ، من فضلك لا تأنيب :)}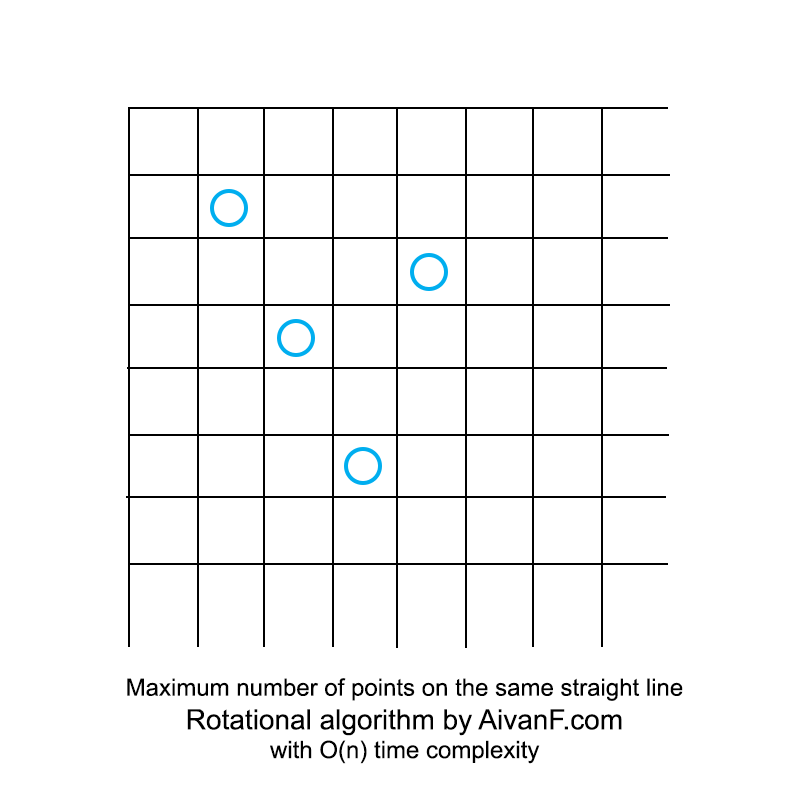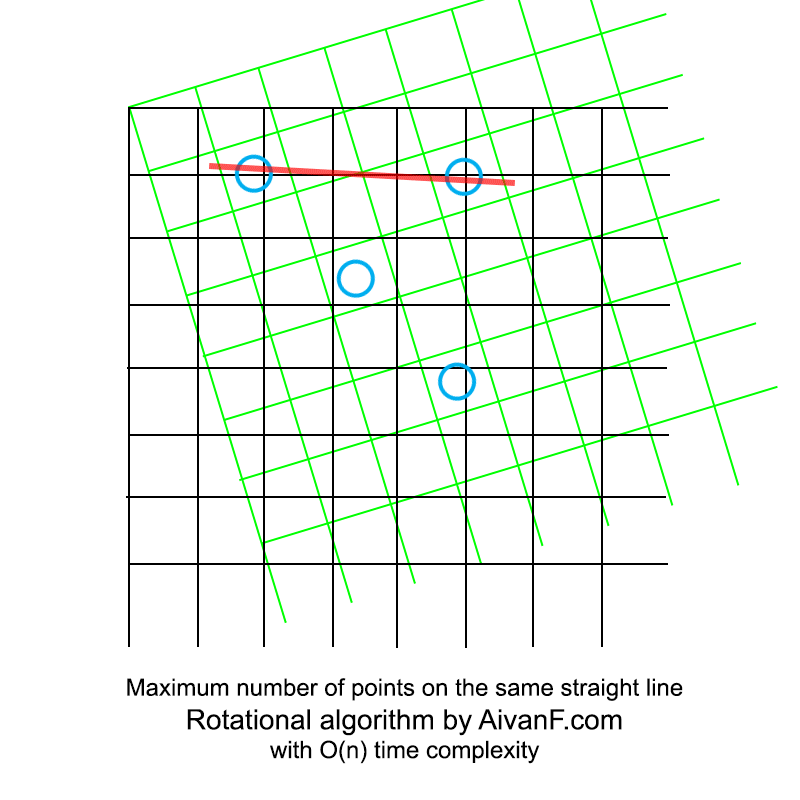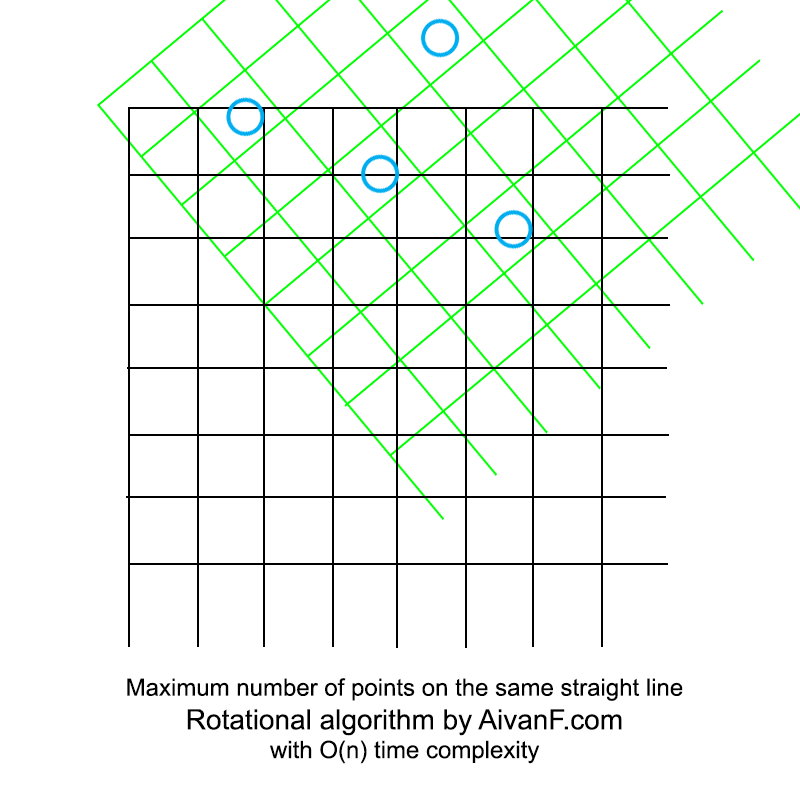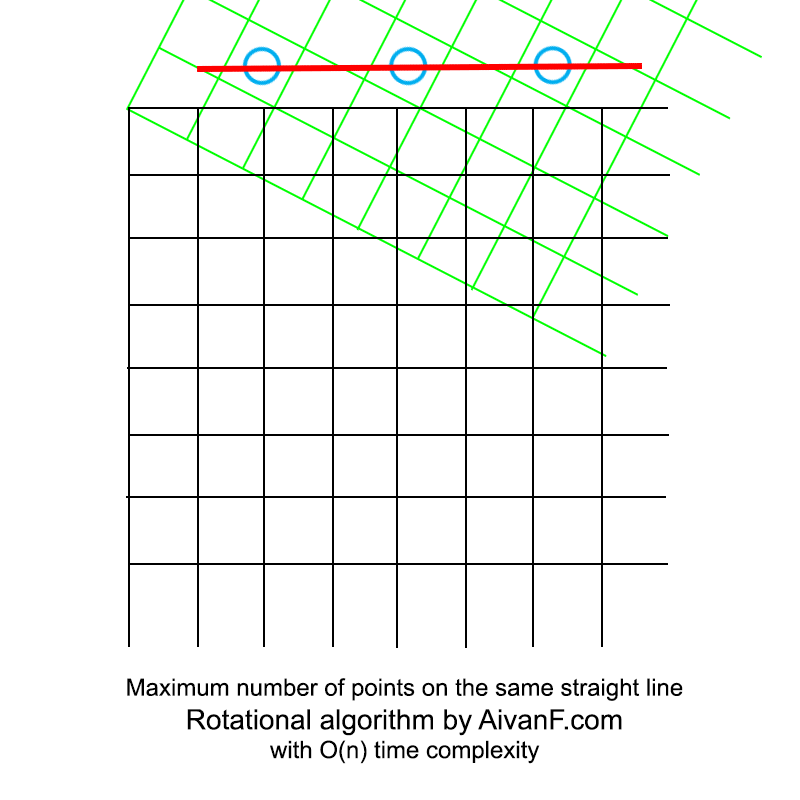



ومن المثير للاهتمام أن نلاحظ أن التنفيذ اللاحق للبحث الشامل تناول المزيد من سطور الكود.

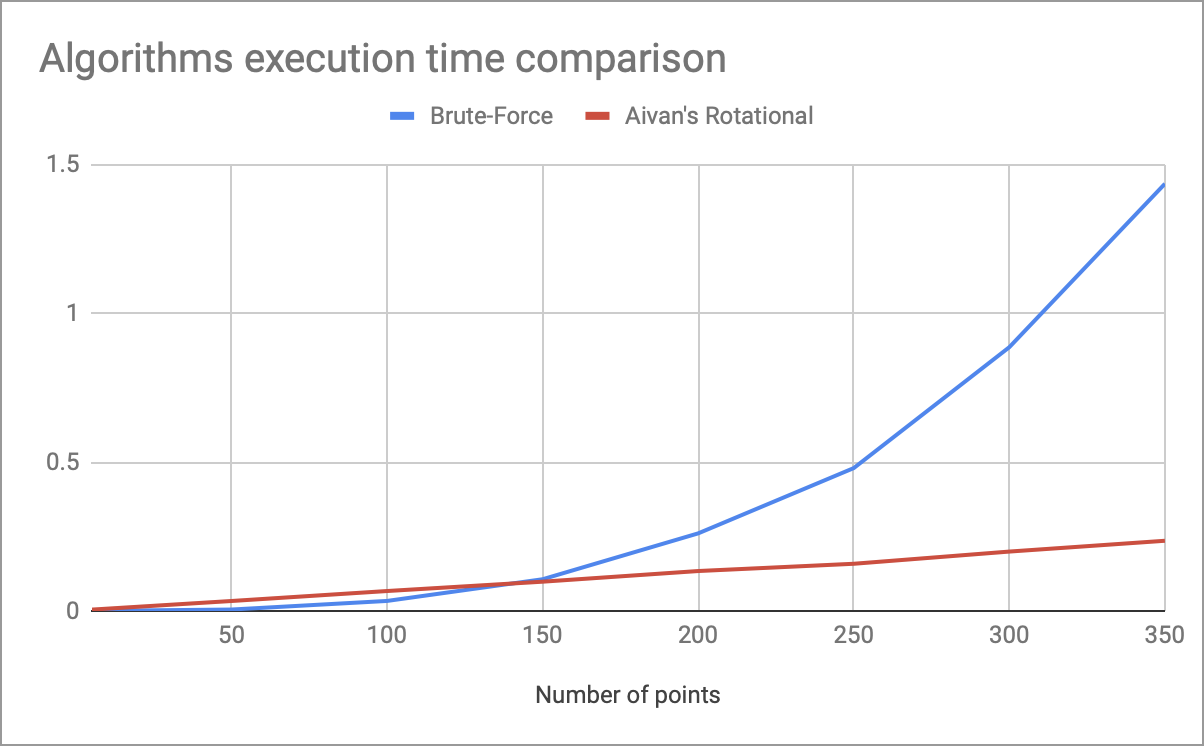
الرسم البياني مع قياسات وقت تشغيل خوارزمية الدوران الخاصة بي والتعداد الكامل بناءً على عدد النقاط في الرأس.


تظهر حوالي 150 نقطة ميزة التعقيد الخطي في الوقت المناسب (مع المعاملات المستخدمة في الكود أعلاه). نتيجة لذلك ، تحتوي هذه الخوارزمية على العيوب التالية:

• دقة ليست مطلقة.
• وقت التشغيل على مجموعات صغيرة من النقاط طويلة.
  _{بشكل عام ، يتم تصحيح هذا بسهولة من خلال مجموعة مختصة من المعاملات: بالنسبة للمجموعات البسيطة ، ROT_COUNT = 36 بدلاً من 2000 كافية ، مما يزيد من الكود 50+ مرة.}

وهذه المزايا:

• إنه يعمل بهدوء مع الإحداثيات الكسرية.
• التعقيد الزمني خطي ، وهو ملحوظ في مجموعات البيانات الكبيرة.

جدول مع القياسات متاح هنا . رمز مصدر كامل للمشروع مع كل من الخوارزميات والشيكات المختلفة على GitHub .

التحديث. أريد أن أشير مرة أخرى إلى أن هذه الخوارزمية لها مزايا وعيوب على حد سواء ، وأنا لا أدعو إليها كبديل مثالي للقوة الغاشمة ، لقد وصفت للتو بديلاً ممكنًا مثيرًا للاهتمام ، والذي قد يكون في بعض الحالات أكثر ملاءمة.