حل الكلمات المتقاطعة اليابانية باستخدام P̶y̶t̶h̶o̶̶n̶ Rust و WebAssembly

كيفية عمل محلل nonogram لبرنامج Python ، أعد كتابته إلى Rust ، بحيث يمكن تشغيله مباشرة في المستعرض عبر WebAssembly.

TL ؛ د

بداية

حول الكلمات المتقاطعة اليابانية (nonograms) على Habré كان هناك بالفعل العديد من المشاركات. مثال
واحد آخر .

يتم تشفير الصور بأرقام موجودة على يسار الصفوف ، وكذلك أعلى الأعمدة. يُظهر عدد الأرقام عدد مجموعات خلايا الأسود (أو اللون ، لكلمات الكلمات المتقاطعة) الموجودة في الصف أو العمود المقابل ، والأرقام نفسها - عدد الخلايا المدمجة التي تحتوي عليها كل مجموعة من هذه المجموعات (على سبيل المثال ، مجموعة من ثلاثة أرقام - 4 ، 1 ، و 3 يعني أنه في هذا الصف توجد ثلاث مجموعات: الأولى - من أربع ، والثانية - من واحدة ، والثالثة - من ثلاث خلايا سوداء). في أحجية الكلمات المتقاطعة بالأبيض والأسود ، يجب فصل المجموعات بخلية فارغة واحدة على الأقل ؛ في الكلمات المتقاطعة الملونة ، تنطبق هذه القاعدة على المجموعات ذات اللون الواحد فقط ، ويمكن أن تكون المجموعات متعددة الألوان متباعدة عن كثب (يمكن أن تكون الخلايا الفارغة على طول حواف الصفوف). من الضروري تحديد موقع مجموعات الخلايا.

واحدة من أكثر وجهات النظر المقبولة عمومًا هي أنه لا يمكن استدعاء الكلمات المتقاطعة "الصحيحة" إلا تلك التي تم حلها بطريقة "منطقية". يسمى هذا عادةً طريقة الحل التي لا تؤخذ في الاعتبار التبعيات بين الصفوف و / أو الأعمدة المختلفة. بمعنى آخر ، الحل هو سلسلة من القرارات المستقلة للصفوف أو الأعمدة الفردية حتى يتم ملء جميع الخلايا (المزيد حول الخوارزمية أدناه). على سبيل المثال ، يمكن العثور على هذه الصور غير المدون عليها فقط على موقع الويب http://nonograms.org/ ( http://nonograms.ru/ ). تم الإشارة بالفعل إلى الصور غير المقتبسة من هذا الموقع كمثال في مقالة " حل الكلمات المتقاطعة اليابانية الملونة بسرعة الضوء" . لأغراض المقارنة والتحقق ، أضاف حلالي أيضًا دعمًا لتنزيل الكلمات المتقاطعة وتحليلها من هذا الموقع (بفضل KyberPrizrak للحصول على إذن لاستخدام مواد من موقعه).

ومع ذلك ، يمكن توسيع مفهوم nonograms إلى مشكلة أكثر عمومية ، عندما تؤدي الطريقة "المنطقية" المعتادة إلى طريق مسدود. في مثل هذه الحالات ، يتعين على المرء أن يتخذ افتراضًا حول لون الخلية ، وبعد أن يثبت أن هذا اللون يؤدي إلى تناقض ، حدد اللون المقابل لهذه الخلية. تسلسل هذه الخطوات يمكن (إذا كان لديك الصبر) أن يقدم لنا جميع الحلول. ستتمحور هذه المقالة حول حل مثل هذه الكلمات المتقاطعة بشكل عام.

الثعبان

منذ حوالي عام ونصف ، تعثرت بطريق الخطأ على مقال وصف طريقة لحل سطر واحد (كما اتضح فيما بعد ، كانت الطريقة بطيئة إلى حد ما).

عندما طبقت هذه الطريقة في Python (لغتي الرئيسية) وأضفت تحديثًا متسلسلًا لكل الخطوط ، رأيت أن كل هذا لم يتم حله بسرعة كبيرة. بعد دراسة العتاد ، اتضح أن هناك العديد من الأعمال والتطبيقات التي تقدم مقاربات مختلفة لهذه المهمة حول هذا الموضوع.

يبدو لي أن العمل الأكثر طموحاً في تحليل تطبيقات حلال مختلف تم تنفيذه بواسطة جان وولتر ، الذي نشر على موقعه (والذي ، حسب علمي ، لا يزال أكبر مستودع عام لغير المدونين على الإنترنت) ، دراسة مفصلة تحتوي على مجموعة كبيرة من المعلومات والروابط التي يمكن أن تساعد في خلق حلالا الخاصة بك.

بدراسة مصادر عديدة (ستكون في نهاية المقال) ، قمت بتحسين سرعة وفاعلية ملفي التدريجي. وكنتيجة لذلك ، كنت مدمنًا وشاركت في تنفيذ خوارزميات وتجديدها وتصحيحها لمدة 10 أشهر تقريبًا في وقت الفراغ من العمل.

الخوارزميات الأساسية

يمكن تمثيل المحلل الناتج في شكل أربعة مستويات للقرار:

• ( سطر ) حلالي خطي: ​​عند الإدخال ، سطر من الخلايا وخط وصف (أدلة) ، عند الإخراج ، سطر حل جزئي. في حل python ، قمت بتنفيذ 4 خوارزميات مختلفة (3 منها تم تكييفها للكلمات المتقاطعة اللون). الأسرع تبين أن خوارزمية BguSolver ، سميت باسم المصدر الأصلي . هذا هو وسيلة فعالة للغاية وموحدة تقريبا لحل سلاسل nonogram باستخدام البرمجة الديناميكية. يمكن العثور على الرمز السري لهذه الطريقة ، على سبيل المثال ، في هذه المقالة .

  
  

• ( نشر ) نضع كل الصفوف والأعمدة في قائمة انتظار ، ونستعرضها باستخدام حلال خطي ، عندما نتلقى معلومات جديدة عند حل صف (عمود) ، نقوم بتحديث قائمة الانتظار ، على التوالي ، بأعمدة جديدة (صفوف). تابع حتى السطر فارغ.

  
  
  مثال ورمز

  نحن نأخذ المهمة التالية لحلها من قائمة الانتظار. اجعلها عبارة عن سلسلة فارغة (لم يتم حلها) بطول 7 (نشير إليها على أنها ??????? ) مع وصف للكتل [2, 3] . سوف تنتج حلالا خطي سلسلة حل جزئيا ?X??XX? حيث X هي الخلية المملوءة. عند تحديث الصف ، نرى أن الأعمدة التي تحتوي على أرقام 1 و 4 و 5 قد تغيرت (تبدأ الفهرسة عند 0). هذا يعني أن معلومات جديدة ظهرت في الأعمدة المشار إليها ويمكن إعادتها إلى محلل "الخطي". نضع هذه الأعمدة في قائمة انتظار المهام ذات الأولوية العليا (من أجل إعطائها إلى حلال الخطي التالي).

  
  

   def propagation(board): line_jobs = PriorityDict() for row_index in range(board.height): new_job = (False, row_index) line_jobs[new_job] = 0 for column_index in range(board.width): new_job = (True, column_index) line_jobs[new_job] = 0 for (is_column, index), priority in line_jobs.sorted_iter(): new_jobs = solve_and_update(board, index, is_column) for new_job in new_jobs: # upgrade priority new_priority = priority - 1 line_jobs[new_job] = new_priority def solve_and_update(board, index, is_column): if is_column: row_desc = board.columns_descriptions[index] row = tuple(board.get_column(index)) else: row_desc = board.rows_descriptions[index] row = tuple(board.get_row(index)) updated = line_solver(row_desc, row) if row != updated: for i, (pre, post) in enumerate(zip(row, updated)): if _is_pixel_updated(pre, post): yield (not is_column, i) if is_column: board.set_column(index, updated) else: board.set_row(index, updated) 

  
  
  
  

• ( اختبار ) لكل خلية لم يتم حلها ، نقوم بالفرز بين جميع خيارات الألوان ونحاول الانتشار باستخدام هذه المعلومات الجديدة. إذا حصلنا على تناقض ، فإننا نخرج هذا اللون من خيارات الألوان للخلية ونحاول الاستفادة منه مرة أخرى باستخدام التكاثر. إذا تم حلها حتى النهاية ، فنحن نضيف الحل إلى قائمة الحلول ، لكننا نستمر في تجربة الألوان الأخرى (قد يكون هناك عدة حلول). إذا توصلنا إلى موقف يستحيل فيه الحل ، فإننا نتجاهل ونكرر الإجراء باستخدام خلية / لون مختلف.

  
  
  قانون

  إرجاع صحيح إذا تم تلقي تناقض نتيجة العينة.

  
  

   def probe(self, cell_state): board = self.board pos, assumption = cell_state.position, cell_state.color # already solved if board.is_cell_solved(pos): return False if assumption not in board.cell_colors(pos): LOG.warning("The probe is useless: color '%s' already unset", assumption) return False save = board.make_snapshot() try: board.set_color(cell_state) propagation( board, row_indexes=(cell_state.row_index,), column_indexes=(cell_state.column_index,)) except NonogramError: LOG.debug('Contradiction', exc_info=True) # rollback solved cells board.restore(save) else: if board.is_solved_full: self._add_solution() board.restore(save) return False LOG.info('Found contradiction at (%i, %i)', *pos) try: board.unset_color(cell_state) except ValueError as ex: raise NonogramError(str(ex)) propagation( board, row_indexes=(pos.row_index,), column_indexes=(pos.column_index,)) return True 

  
  
  
  

• ( التراجع ) إذا لم تتجاهل أثناء اللغز لغزًا تم حله جزئيًا ، لكنك استمرت في التكرار المتكرر للإجراء نفسه ، فسنعود إلى التراجع (بمعنى آخر ، السير الكامل في عمق شجرة القرارات المحتملة). هنا ، يبدأ دور كبير يلعبه ، أي من الخلايا سيتم اختياره كملحق التالي للحل المحتمل. بحث جيد حول هذا الموضوع في هذا المنشور .

  
  
  قانون

  التراجع هو فوضوي للغاية معي ، ولكن هاتين الوظيفتين تصفان ما يحدث تقريبًا أثناء البحث المتكرر

  
  

   def search(self, search_directions, path=()): """ Return False if the given path is a dead end (no solutions can be found) """ board = self.board depth = len(path) save = board.make_snapshot() try: while search_directions: state = search_directions.popleft() assumption, pos = state.color, state.position cell_colors = board.cell_colors(pos) if assumption not in cell_colors: LOG.warning("The assumption '%s' is already expired. " "Possible colors for %s are %s", assumption, pos, cell_colors) continue if len(cell_colors) == 1: LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally', pos, assumption) try: self._solve_without_search() except NonogramError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The path %s is invalid", assumption, pos, path) return False if board.is_solved_full: self._add_solution() LOG.warning( "The only color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True continue rate = board.solution_rate guess_save = board.make_snapshot() try: LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)', state, depth, rate, path) success = self._try_state(state, path) finally: board.restore(guess_save) if not success: try: LOG.warning( "Unset the color %s for cell '%s'. Solve it unconditionally", assumption, pos) board.unset_color(state) self._solve_without_search() except ValueError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The whole branch (depth=%d) is invalid. ", assumption, pos, depth) return False if board.is_solved_full: self._add_solution() LOG.warning( "The negation of color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True finally: # do not restore the solved cells on a root path - they are really solved! if path: board.restore(save) return True def _try_state(self, state, path): board = self.board full_path = path + (state,) probe_jobs = self._get_all_unsolved_jobs(board) try: # update with more prioritized cells for new_job, priority in self._set_guess(state): probe_jobs[new_job] = priority __, best_candidates = self._solve_jobs(probe_jobs) except NonogramError as ex: LOG.warning('Dead end found (%s): %s', full_path[-1], str(ex)) return False rate = board.solution_rate LOG.info('Reached rate %.4f on %s path', rate, full_path) if rate == 1: return True cells_left = round((1 - rate) * board.width * board.height) LOG.info('Unsolved cells left: %d', cells_left) if best_candidates: return self.search(best_candidates, path=full_path) return True 

  
  
  
  

لذلك ، نبدأ في حل اللغز الخاص بالكلمات المتقاطعة من المستوى الثاني (الأول مناسب فقط لحالة الانحطاط ، عندما يكون في الألغاز المتقاطعة بأكملها صف واحد أو عمود واحد فقط) وننتقل تدريجياً إلى أعلى. كما قد تتخيل ، كل مستوى يتسبب في المستوى الأساسي عدة مرات ، لذلك من أجل إيجاد حل فعال ، من الضروري للغاية الحصول على مستويين أول والثاني بسرعة ، والتي يمكن استدعاء ملايين المرات لألغاز معقدة.

في هذه المرحلة ، اتضح (بشكل متوقع إلى حد ما) أن الثعبان ليس على الإطلاق الأداة المناسبة لأقصى قدر من الأداء في مهمة كثيفة وحدة المعالجة المركزية: فكل العمليات الحسابية فيها غير فعالة للغاية مقارنة باللغات ذات المستوى الأدنى. على سبيل المثال ، تبين أن أكثر أدوات تحليل BGU حلالاً (في جافا) وفقًا لنتائج نتائج القياسات ، كانت أسرع من 7 إلى 17 (أحيانًا ما يصل إلى 27) مرات في مجموعة متنوعة من المهام.

         pynogram_my BGU_my تسريع
 راقصة 0.976 0.141 6.921986      
 Cat 1.064 0.110 9.672727      
 Skid 1.084 0.101 10.732673     
 باكز 1.116 0.118 9.457627      
 Edge 1.208 0.094 12.851064     
 دخان 1.464 0.120 12.200000     
 العقدة 1.332 0.140 9.514286      
 سوينغ 1.784 0.138 12.927536     
 أمي 2.108 0.147 14.340136     
 DiCap 2.076 0.176 11.795455     
 التراجيد 2.368 0.265 8.935849      
 Merka 2.084 0.196 10.632653     
 بترو 2.948 0.219 13.461187     
 إم آند إم 3.588 0.375 9.568000      
 وقعت 4.068 0.242 16.809917     
 خفيف 3.848 0.488 7.885246      
 للأبد 111.000 13.570 8.179808  
 المركز 5.700 0.327 17.431193     
 Hot 3.150 0.278 11.330935     
 الكاراتيه 2.500 0.219 11.415525     
 9-دوم 510.000 70.416 7.242672      
 العلم 149.000 5.628 26.474769     
 أسد 71.000 2.895 24.525043     
 مارلي 12.108 4.405 2.748695      
 الشيء 321.000 46.166 6.953169      
 Nature inf 433.138 inf     
 Sierp الوقود النووي المشع NaN      
 Gettys الوقود النووي المشع NaN      

وهذا بالفعل بعد أن بدأت باستخدام PyPy ، وعلى CPython القياسي ، كان وقت الحساب أطول من PyPy 4-5 مرات! يمكننا أن نقول أن أداء محلل جافا مماثل تحول إلى 28-85 مرة أعلى من رمز CPython.

أدت محاولات تحسين أداء برنامج Solver الخاص بي باستخدام ملفات التعريف (cProfile و SnakeViz و line_profiler) إلى حدوث بعض التسارع ، لكنها بالطبع لم تعطي نتيجة غريبة.

ملخص :

+ حل Solver يمكنه حل جميع الألغاز من المواقع https://webpbn.com و http://nonograms.org وتنسيقه (ini-based)

+ يحل الصور بالأبيض والأسود والألوان غير الرسومية بأي عدد من الألوان (الحد الأقصى لعدد الألوان التي حققتها هو 10)

+ يحل الألغاز مع أحجام كتلة في عداد المفقودين (blotted). مثال على مثل هذا اللغز .

+ يمكن تقديم الألغاز إلى وحدة التحكم / إلى اللعنات / النافذة في المتصفح (عند تثبيت خيار الويب pynogram إضافية). بالنسبة إلى جميع الأوضاع ، يتم دعم عرض تقدم الحل في الوقت الفعلي.

- العمليات الحسابية البطيئة (مقارنة بالتطبيقات الموضحة في مقالة مقارنة المذيبات ، انظر الجدول ).

- التراجع غير الفعال: يمكن حل بعض الألغاز لساعات (عندما تكون شجرة القرارات كبيرة جدًا).

صدأ

في بداية العام ، بدأت دراسة الصدأ. لقد بدأت ، كالعادة ، مع The Book ، التي تعرفت على WASM ، من خلال البرنامج التعليمي المقترح . ومع ذلك ، أردت بعض المهام الحقيقية التي يمكنك من خلالها المشاركة في نقاط القوة في اللغة (في المقام الأول أدائها الفائق) ، وليس بعض الأمثلة التي اخترعها شخص ما. لذلك عدت إلى nonograms. لكن الآن لدي بالفعل نسخة صالحة من جميع الخوارزميات في بيثون ، فقد تركت لإعادة كتابة "فقط".

كانت الأخبار الجيدة تتوقعني من البداية: اتضح أن Rust ، مع نظام النوع الخاص به ، يصف بشكل مثالي هياكل البيانات لمهمتي. على سبيل المثال ، واحدة من المراسلات الأساسية BinaryColor + BinaryBlock / MultiColor + ColoredBlock تتيح لك إمكانية الفصل بشكل دائم بين الصور بالأبيض والأسود واللون. إذا حاولنا في مكان ما في التعليمة البرمجية حل سلسلة ملونة باستخدام كتل وصف ثنائية عادية ، فسوف نحصل على خطأ في الترجمة حول عدم تطابق النوع.

 pub trait Color { fn blank() -> Self; fn is_solved(&self) -> bool; fn solution_rate(&self) -> f64; fn is_updated_with(&self, new: &Self) -> Result<bool, String>; fn variants(&self) -> Vec<Self>; fn as_color_id(&self) -> Option<ColorId>; fn from_color_ids(ids: &[ColorId]) -> Self; } pub trait Block { type Color: Color; fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self { let size = s.parse::<usize>().expect("Non-integer block size given"); Self::from_size_and_color(size, color) } fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self; fn size(&self) -> usize; fn color(&self) -> Self::Color; } #[derive(Debug, PartialEq, Eq, Hash, Clone)] pub struct Description<T: Block> where T: Block, { pub vec: Vec<T>, } // for black-and-white puzzles #[derive(Debug, PartialEq, Eq, Hash, Copy, Clone, PartialOrd)] pub enum BinaryColor { Undefined, White, Black, BlackOrWhite, } impl Color for BinaryColor { // omitted } #[derive(Debug, PartialEq, Eq, Hash, Default, Clone)] pub struct BinaryBlock(pub usize); impl Block for BinaryBlock { type Color = BinaryColor; // omitted } // for multicolor puzzles #[derive(Debug, PartialEq, Eq, Hash, Default, Copy, Clone, PartialOrd, Ord)] pub struct MultiColor(pub ColorId); impl Color for MultiColor { // omitted } #[derive(Debug, PartialEq, Eq, Hash, Default, Clone)] pub struct ColoredBlock { size: usize, color: ColorId, } impl Block for ColoredBlock { type Color = MultiColor; // omitted } 

عند نقل الكود ، أشارت بعض النقاط بوضوح إلى أن اللغة المكتوبة بشكل ثابت مثل Rust (جيدًا ، أو على سبيل المثال ، C ++) أكثر ملاءمة لهذه المهمة. بتعبير أدق ، تصف الخصائص العامة والسمات مجالًا أفضل من التسلسلات الهرمية للفئة. لذلك في كود Python ، كان لدي فئتان للحصول على BguSolver خطي ، BguSolver و BguColoredSolver والذي حل خط أبيض وأسود وخط لون ، على التوالي. في كود Rust ، لا يزال لدي struct DynamicSolver<B: Block, S = <B as Block>::Color> العامة الوحيدة struct DynamicSolver<B: Block, S = <B as Block>::Color> ، والتي يمكنها حل كلا النوعين من المهام ، اعتمادًا على النوع الذي تم تمريره أثناء الإنشاء ( DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock> ). هذا ، بالطبع ، لا يعني أنه لا يمكن القيام بشيء مماثل في Python ، فقط في Rust ، أشار نظام الكتابة بوضوح إلى أنك إذا لم تسير بهذه الطريقة ، فسيتعين عليك كتابة الكثير من التعليمات البرمجية المتكررة.

بالإضافة إلى ذلك ، لاحظ أي شخص حاول الكتابة في Rust ، بلا شك تأثير "الثقة" في المحول البرمجي ، عندما تأتي عملية كتابة التعليمات البرمجية إلى خوارزمية ميتا الزائفة التالية:

 write_initial_code
 بينما (compiler_hints = $ (فحص البضائع))! = 0 ؛  فعل
     fix_errors (compiler_hints)
 نهاية

عندما يتوقف المحول البرمجي عن إصدار الأخطاء والتحذيرات ، سيكون كودك متوافقًا مع نظام الكتابة ومدقق الاقتراض ، وسوف تحذر مسبقًا من حدوث مجموعة من الأخطاء المحتملة (بالطبع ، مع مراعاة التصميم الدقيق لأنواع البيانات).

سأقدم بعض الأمثلة للوظائف التي توضح مدى دقة رمز الصدأ (مقارنةً بنظيرات Python).

 def unsolved_neighbours(self, position): for pos in self.neighbours(position): if not self.is_cell_solved(*pos): yield pos 

 fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ { self.neighbours(&point) .into_iter() .filter(move |n| !self.cell(n).is_solved()) } 

             1 2 3 4 5 6 7 8 9 
             _ _ _ _ _ _ _ _ _ _
      2 3 1 | _ | _ | _ | _ | _ | _ | _ | _ | _ | 
               ^ ^ ^
               |  |  |
 نهاية كتلة واحدة |  |  | 
 نهاية الكتلة 2 -------- |
 نهاية الكتلة 3 ------------

 @expand_generator def partial_sums(blocks): if not blocks: return sum_so_far = blocks[0] yield sum_so_far for block in blocks[1:]: sum_so_far += block + 1 yield sum_so_far 

 fn partial_sums(desc: &[Self]) -> Vec<usize> { desc.iter() .scan(None, |prev, block| { let current = if let Some(ref prev_size) = prev { prev_size + block.0 + 1 } else { block.0 }; *prev = Some(current); *prev }) .collect() } 

عند ترقية ، لقد قمت بإجراء العديد من التغييرات

• خضع حلالا الأساسية (خوارزميات) تغييرات طفيفة (في المقام الأول لدعم أنواع عامة للخلايا وكتل)
• غادر الخوارزمية (الأسرع) الوحيدة للحلال الخطي
• بدلاً من تنسيق ini ، قدم تنسيق TOML تم تعديله قليلاً
• لم يضيف دعمًا للكلمات المتقاطعة الموضحة ، لأنه ، بالمعنى الدقيق للكلمة ، هذه فئة مختلفة من المهام

• ترك الطريقة الوحيدة للإخراج - فقط إلى وحدة التحكم ، ولكن الآن يتم رسم الخلايا الملونة في وحدة التحكم بالألوان (بفضل هذا الصندوق )

  
  
  مثل هذا

  

  
  
  
  

أدوات مفيدة

• clippy عبارة عن محلل ثابت قياسي يمكنه أحيانًا تقديم النصائح التي تؤدي إلى زيادة طفيفة في أداء التعليمات البرمجية.
• valgrind هي أداة لتحليل التطبيق الديناميكي. لقد استخدمتها كملف تعريف للبحث عن botneks ( valrgind --tool=callgrind ) وخاصة مقاطع الذاكرة valrgind --tool=massif للشفرة ( valrgind --tool=massif ). نصيحة: اضبط [profile.release] debug = صواب على Cargo.toml قبل بدء برنامج التعريف. سيؤدي ذلك إلى ترك أحرف التصحيح في الملف القابل للتنفيذ.
• kcachegrind لعرض ملفات callgrind. أداة مفيدة للغاية للعثور على الأماكن الأكثر إشكالية من حيث الأداء.

إنتاجية

لذلك ما بدأت إعادة كتابة على الصدأ. نأخذ الكلمات المتقاطعة من جدول المقارنة المذكور بالفعل ونديرها من خلال أفضل الحلول الموضحة في المقالة الأصلية. النتائج ووصف يدير هنا . نحن نأخذ الملف الناتج وننشئ عليه بعض الرسوم البيانية ، حيث أن وقت الحل يختلف من مللي ثانية إلى عشرات الدقائق ، فإن الرسم البياني مصنوع بمقياس لوغاريتمي.

 import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline # strip the spaces df = pd.read_csv('perf.csv', skipinitialspace=True) df.columns = df.columns.str.strip() df['name'] = df['name'].str.strip() # convert to numeric df = df.replace('\+\ *', np.inf, regex=True) ALL_SOLVERS = list(df.columns[3:]) df.loc[:,ALL_SOLVERS] = df.loc[:,ALL_SOLVERS].apply(pd.to_numeric) # it cannot be a total zero df = df.replace(0, 0.001) #df.set_index('name', inplace=True) SURVEY_SOLVERS = [s for s in ALL_SOLVERS if not s.endswith('_my')] MY_MACHINE_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] in SURVEY_SOLVERS] MY_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] not in SURVEY_SOLVERS] bar_width = 0.17 df_compare = df.replace(np.inf, 10000, regex=True) plt.rcParams.update({'font.size': 20}) def compare(first, others): bars = [first] + list(others) index = np.arange(len(df)) fig, ax = plt.subplots(figsize=(30,10)) df_compare.sort_values(first, inplace=True) for i, column in enumerate(bars): ax.bar(index + bar_width*i, df_compare[column], bar_width, label=column[:-3]) ax.set_xlabel("puzzles") ax.set_ylabel("Time, s (log)") ax.set_title("Compare '{}' with others (lower is better)".format(first[:-3])) ax.set_xticks(index + bar_width / 2) ax.set_xticklabels("#" + df_compare['ID'].astype(str) + ": " + df_compare['name'].astype(str)) ax.legend() plt.yscale('log') plt.xticks(rotation=90) plt.show() fig.savefig(first[:-3] + '.png', bbox_inches='tight') for my in MY_SOLVERS: compare(my, MY_MACHINE_SOLVERS) compare(MY_SOLVERS[0], MY_SOLVERS[1:]) 

بيثون حلالا

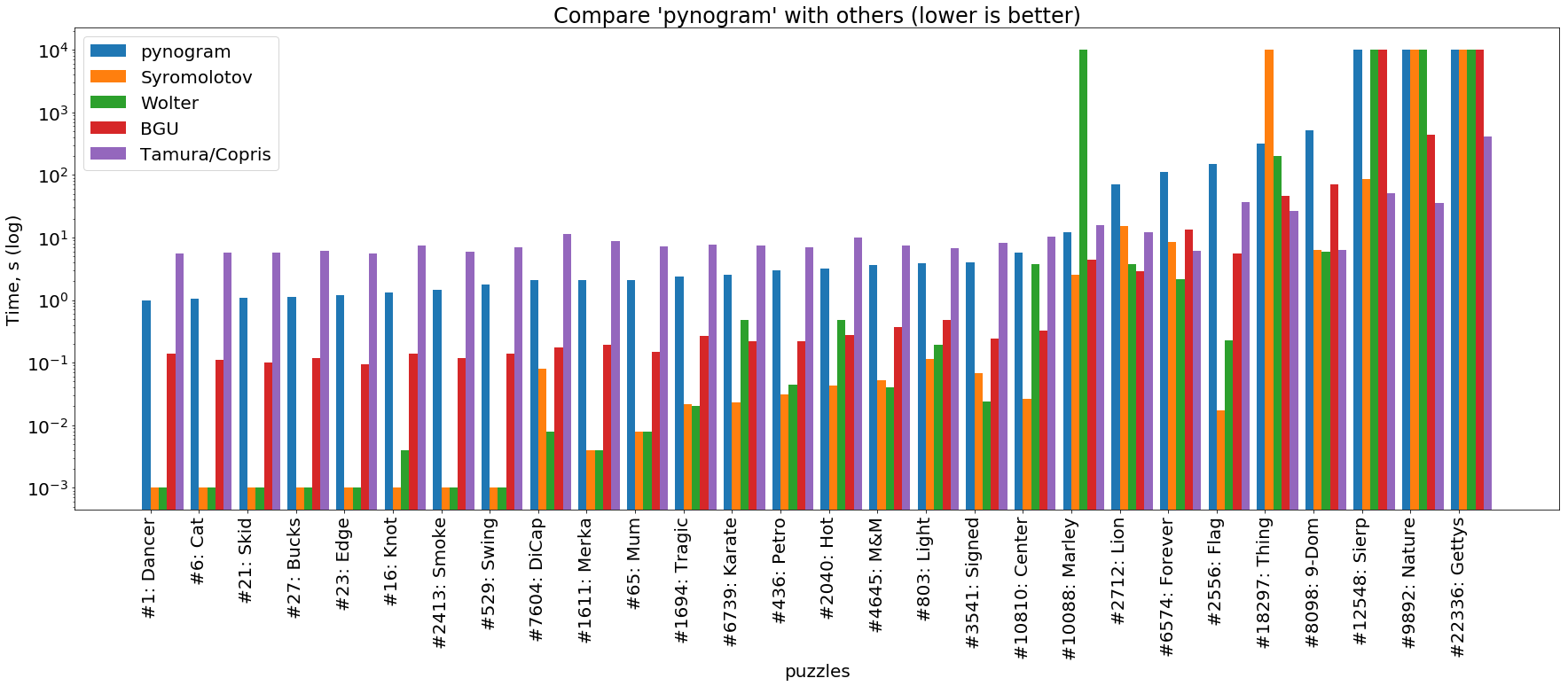
( الصورة قابلة للنقر )

نرى أن الرسم التوضيحي هنا أبطأ من كل المحاليل المقدمة. الاستثناء الوحيد لهذه القاعدة هو حلال تامورا / كوبريس استنادًا إلى SAT ، الذي يحل أبسط الألغاز (الجزء الأيسر من الرسم البياني) أطول من اللغز الخاص بنا. ومع ذلك ، فهذه ميزة من ميزات SAT-solvers: فهي مصممة للكلمات المتقاطعة المعقدة للغاية حيث يتعطل محلل منتظم في التراجع لفترة طويلة. هذا واضح للعيان على الجانب الأيمن من الرسم البياني ، حيث يحل Tamura / Copris أصعب الألغاز بعشرات ومرات أسرع من أي شخص آخر.

حلالا الصدأ

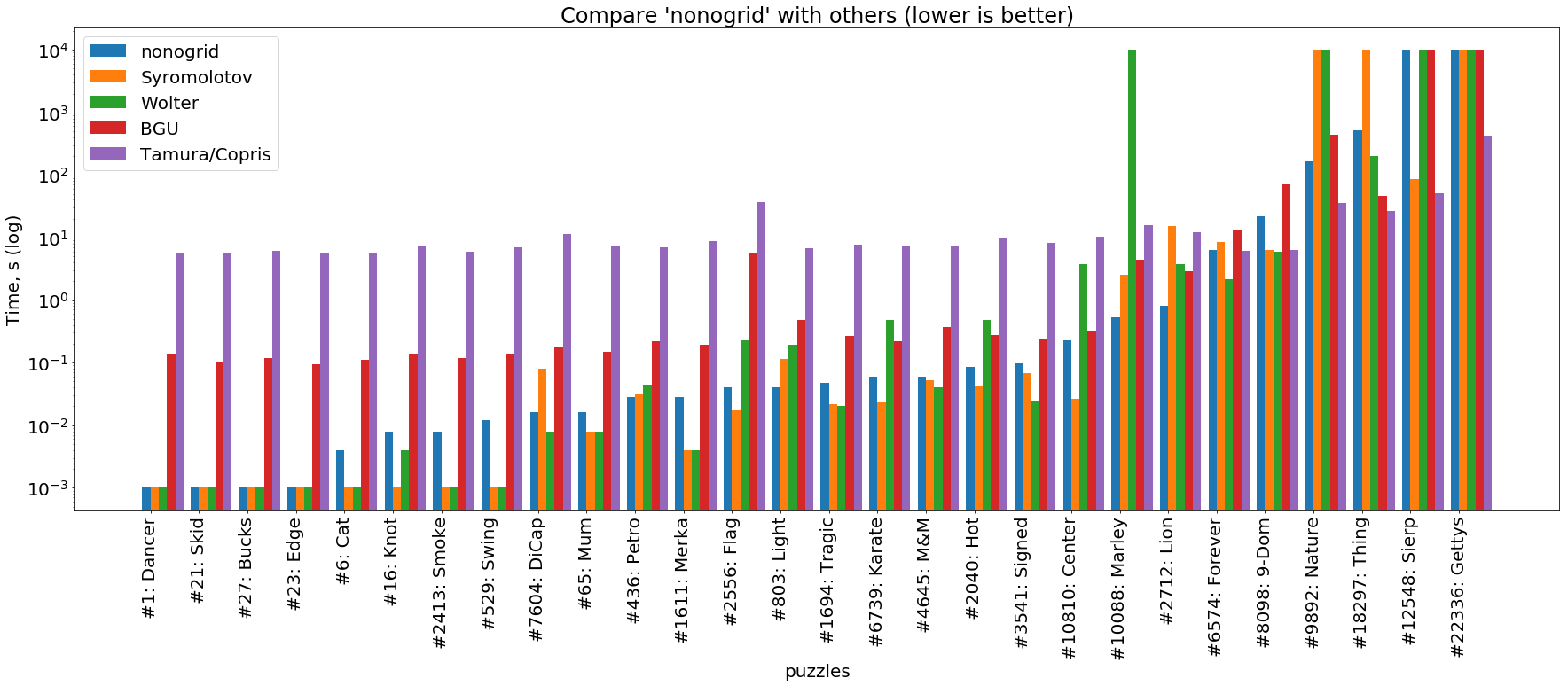
( الصورة قابلة للنقر )

يوضح هذا الرسم البياني أن nonogrid في مهام بسيطة يتواءم أيضًا مع أو أكثر قليلاً من المذيبات عالية الأداء المكتوبة في C و C ++ ( Wolter و Syromolotov ). مع تعقيد المهام ، يكرر حلالا لدينا تقريبا مسار BGU- حلالا (جافا) ، ولكن دائما تقريبا قبل ذلك من قبل حول حجم. في أصعب المهام ، يكون Tamura / Copris دائمًا متقدمًا على الجميع.

الصدأ مقابل بيثون

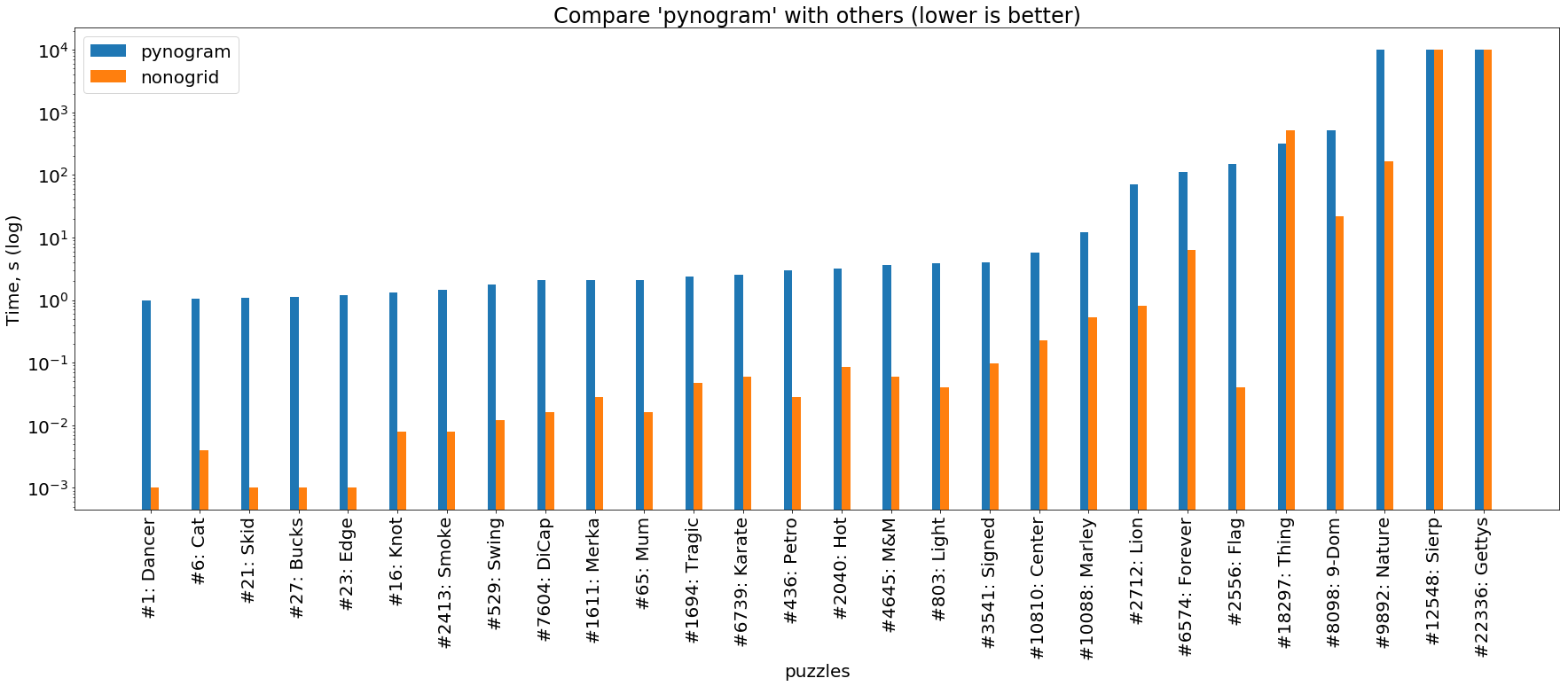
( الصورة قابلة للنقر )

وأخيرًا ، مقارنة بين حلينا الموصوفين هنا. يمكن أن نرى أن حلالا الصدأ دائما تقريبا 1-3 أوامر من حيث الحجم من بيثون حلالا.

ملخص :

+ حل Solver يمكنه حل جميع الألغاز من المواقع https://webpbn.com (باستثناء blotted - بأحجام كتلة مخفية جزئيًا) و http://nonograms.org وتنسيقه (المستند إلى TOML)

+ يحل nonograms بالأبيض والأسود واللون مع أي عدد من الألوان

+ يمكن تقديم الألغاز إلى وحدة التحكم (color c webpbn.com يرسم لونًا حقيقيًا)

+ يعمل بسرعة (مقارنة بالتطبيقات الموضحة في مقالة مقالة بين المذيبات ، انظر الجدول).

- ظل التراجع غير فعال ، كما هو الحال في حل Python: يمكن حل بعض الألغاز (على سبيل المثال ، مثل 20x20 غير المؤذية ) لساعات (عندما تكون شجرة القرارات كبيرة جدًا). ربما بدلاً من التراجع ، يجدر استخدام حلول SAT المذكورة بالفعل على المحور صحيح أن حل SAT الوحيد الذي وجدته على Rust لأول وهلة يبدو غير مكتمل ومهجر.

WebAssembly

لذا ، فإن إعادة كتابة الكود في Rust قد أثمرت: أصبح حلالا أسرع بكثير. ومع ذلك ، فإن Rust يقدم لنا ميزة أخرى رائعة بشكل لا يصدق: التجميع في WebAssembly والقدرة على تشغيل التعليمات البرمجية الخاصة بك مباشرة في المستعرض.

لتنفيذ هذه الميزة ، هناك أداة خاصة لبرنامج Rust توفر المجلدات اللازمة وتولد أداة غليظة لك لتشغيل وظائف Rust بطريقة غير مؤلمة في كود JS - حزمة wasm (+ wasm-bindgen ). تم وصف معظم العمل معها وأدوات مهمة أخرى بالفعل في البرنامج التعليمي Rust و WebAssembly . ومع ذلك ، هناك بضع نقاط اضطررت إلى اكتشافها بنفسي:

• عند القراءة ، فإنه يخلق الشعور بأن البرنامج التعليمي مكتوب بشكل أساسي لمطور JS الذي يريد تسريع الكود الخاص به باستخدام Rust. حسنا ، أو على الأقل لشخص مطلع على الآلية الوقائية الوطنية . بالنسبة لي ، كشخص بعيد عن الواجهة الأمامية ، كان من المدهش أن أجد أنه حتى المثال القياسي من الكتاب لا يريد العمل مع خادم ويب تابع لجهة خارجية يختلف عن npm run start .

  
  

  لحسن الحظ ، يحتوي wasm-pack على وضع يسمح لك بإنشاء كود JS منتظم (وهو ليس وحدة npm). wasm-pack build --target no-modules --no-typescript لن يعطي wasm-pack build --target no-modules --no-typescript سوى ملفين في الإخراج: project-name.wasm - ثنائي كود Rust الذي تم تجميعه في WebAssembly و project-name.js . يمكن إضافة الملف الأخير إلى أي صفحة HTML <script src="project-name.js"></script> واستخدام وظائف WASM دون عناء مع npm و webpack و ES6 والوحدات النمطية وغيرها من أفراح مطور JS الحديث. يعتبر وضع no-modules مثاليًا للمطورين غير الأماميين أثناء تطوير تطبيق WASM ، فضلاً عن الأمثلة والعروض التوضيحية ، لأنه لا يتطلب أي بنية تحتية إضافية للواجهة الأمامية.

  
  

• يعد WebAssembly مفيدًا للمهام التي تكون ثقيلة للغاية بالنسبة لجافا سكريبت. بادئ ذي بدء ، هذه هي المهام التي تؤدي العديد من العمليات الحسابية. وإذا كان الأمر كذلك ، يمكن تنفيذ هذه المهمة لفترة طويلة حتى مع WebAssembly وبالتالي تنتهك المبدأ غير المتزامن للويب الحديث. أنا أتحدث عن كل أنواع التحذير: برنامج نصي غير مستجيب حدث لي ملاحظته عندما كان حالي يعمل. لحل هذه المشكلة ، يمكنك استخدام آلية عامل الويب . في هذه الحالة ، قد يبدو مخطط العمل مع وظائف WASM "الثقيلة" كما يلي:

  
  
  1. من البرنامج النصي الرئيسي لحدث ما (على سبيل المثال ، النقر فوق زر) ، أرسل رسالة إلى العامل مع مهمة إطلاق وظيفة ثقيلة.
  2. , .
  3. - ()
  
  

WASM- JS, WASM . - ( ), HashMap , . ( JS) , / .

, Mutex , thread-safe. smart- . thread-safe Rc Arc RefCell RwLock . : 30%. --features=threaded thread-safe , WASM-.

6574 8098 ( 10 ):

, - 40..70% , , (32..37%) thread-safe ( cargo build --release --features=threaded ).

Firefox 67.0 Chromium 74.0.

WASM- ( ). https://webpbn.com/ http://www.nonograms.org/

TODO

• "" /, / .

  
  

• , . "" , , . .

  
  

• ( , 3600 ). WASM , ( , (!) , , WASM). , , - , nonogrid .

  
  

• . : , , WASM . , ( ) , JS , .

  
  

• JS. backtrace, .

  
  

• ( TOML- )

  
  

النتائج

• , (, , etc).

  
  

• Rust 1-3 PyPy 1.5-2 ( ).

  
  

• Python Rust , Python (, , comprehensions), Rust-.

  
  

• Rust WebAssembly . Rust , WASM, ( 1.5 ).

  
  

1. The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
2. The BGU Nonograms Project
3. Solving Nonograms by combining relaxations
4. An Efficient Approach to Solving Nonograms
6. Color and black and white Japanese crosswords on-line
8. 'Nonolib' library by Dr. Steven Simpson
9. Rust and WebAssembly