لعب تتريس في AR

حدث لي فكرة غريبة بعض الشيء أن المنزل يمكن أن يكون منصة جيدة للعب Tetris. لم يكن بعيدًا عني سوى مبنى واحد مناسب لهذا الغرض. يمكن رؤية النتيجة في الفيديو:


يتم تنفيذ المشروع على مستوى منخفض إلى حد ما ، دون استخدام أي حل جاهز.

شفرة المصدر

في الغالب يستخدمون خيارين لتطبيق الواقع المعزز:

• عديم المعنى ، أي يتم تحديد موضع الكاميرا من خلال حركة النقاط الرئيسية في دفق الفيديو الخاص بها ؛
• الصورة كعلامة نسبة إلى موضع الكاميرا.

لا تتطلب هذه التطبيقات إعدادًا خاصًا أو شروطًا خاصة.

هناك خيار تنفيذ آخر - للتعرف على كائن محدد واستخدامه كعلامة. هذا يتطلب وجوده على الأقل ، ولكنه يتيح التحكم فيه بصريًا. واحدة من طرق هذا الاعتراف هو اكتشاف كائن من الحواف. له قيود - يجب أن يكون لكائن العلامة حواف محددة بوضوح ، أي يجب أن يكون الكائن صلبًا على الأرجح.

أو يجب أن تكون الحواف محددة بوضوح ، مثل إضاءة هذا المبنى:



يمكن ملاحظة أن الإضاءة الخلفية يمكن فصلها بسهولة في الصورة واستخدامها للكشف.

تطبيق

على كيو تي. يتيح لك هذا الإطار العمل على منصات مختلفة وفي نفس الوقت باستخدام C ++. نظرًا لأن الأداء مهم بالنسبة لنا ، فإن الايجابيات تبدو خيارًا واضحًا.

على الرغم من أن Qt لا يعمل بشكل جيد مع نظام Android (التشغيل الطويل ، تم تعطيل تصحيح الأخطاء) ، ولكن تم تصحيح كل ذلك من خلال القدرة على تصحيح الخوارزمية على سطح المكتب.

تم عرض الرسومات ثلاثية الأبعاد على برنامج OpenGL الخام المدمج في كيو تي.

نفذ العمل مع الكاميرا من خلال كيو تي. تم تسجيل مقطع فيديو للتصحيح ، وكان من المناسب بدرجة كافية استبدال دفق الفيديو الخاص بالكاميرا بدفق فيديو من ملف.

تم تنفيذ الإخراج من خلال أدوات qml. لتكوين صداقات qml و OpenGL لم يكن من دون مشاكل ، لكننا لن نتحدث عن ذلك.

لمعالجة الصور ، مكتبة OpenCV متصلة.

تتبع الخوارزمية

الآن دعنا ننتقل إلى الجزء الأكثر إثارة للاهتمام - الخوارزمية لتتبع كائن على حوافه.
وابدأ بتسليط الضوء على الحواف في الصورة. جميع الحواف في حالتنا لها شكل خطوط مستقيمة ، لذلك فإن الفكرة الأولى التي تتبادر إلى الذهن هي استخدام كاشف الخط. يمكن استخدام التحويلات الصعبة ككاشف للخط. ومع ذلك ، يبدو لي بهذه الطريقة غير صحيح ، لأن تحويل Hough مكلف للغاية ، علاوة على ذلك ، هذا الكاشف ليس موثوقًا به للغاية (هذا شخصي ، وربما يعتمد كل شيء على المهمة).
بدلاً من ذلك ، دعنا نذهب بطريقة مختلفة أكثر عمومية. لن نأخذ في الاعتبار أن خطوطنا مستقيمة ، لكننا سنعمل ببساطة على صورة ثنائية. سيتم تشفير وجود الحواف في الصورة الثنائية. أي تعني البيكسل بقيمة الصفر وجود حافة في هذا المكان ، وتكون قيمة البيكسل أكبر من الصفر - لا توجد حافة. يمكن الحصول على مثل هذه الصورة باستخدام كاشف حدود Canny أو باستخدام تحول بسيط. يمكن العثور على هذه الخوارزميات في OpenCV.

يوجد أيضًا في OpenCV وظيفة أخرى مفيدة بالنسبة لنا الآن - المسافة التحويل ، والتي تأخذ صورة ثنائية عند الإدخال وتعطي صورة عند الإخراج ، بالبكسل التي يتم تشفير المسافة إلى أقرب بكسل.

لنفترض الآن أن لدينا بالفعل تقريب أول جيد للمكان الذي يجب أن يوجد به نموذجنا. بعد ذلك ، نقوم بوصف وظيفة الخطأ ، والتي توضح إلى أي مدى لا تتوافق حواف التقريب مع الحواف في الصورة الناتجة. باستخدام الصورة من distanceTransform ، نحن قادرون بالفعل على القيام بذلك. ثم نقوم بتشغيل خوارزمية تحسين الوظيفة ، مع تغيير تقريبنا فقط لموضع الكائن في الفضاء. نتيجة لذلك ، يجب أن يصف تقريبنا بدقة الموقف الحقيقي للكائن.
نتيجة لذلك ، يمكن تقسيم الخوارزمية إلى مرحلتين:

1. المعالجة المسبقة للصورة - الترميز الثنائي والترشيح واستخدام وظيفة distanceTransfrom.
2. تتبع - تحسين وظيفة الخطأ.

معالجة الصور

في هذه المرحلة ، تحتاج إلى إبراز الحواف في الصورة. يمكنك استخدام كاشف حدود Canny ، ولكن في حالتنا ، يعمل تحويل العتبة المعتاد أو نسخته التكييفية بشكل أفضل (في OpenCV ، تكون هذه عتبات أو عتبتين قابلتين للتكيف). من الواضح أنه سيكون هناك ضجيج على مثل هذه الصورة ، لذلك يلزم التصفية. لنقم بذلك على النحو التالي - حدد الكنتور باستخدام وظيفة OpenCV findCountours وحذف شرائح صغيرة جدًا أو لا تكفي مثل السطر.

يمكن رؤية نتيجة المعالجة في الصورة:



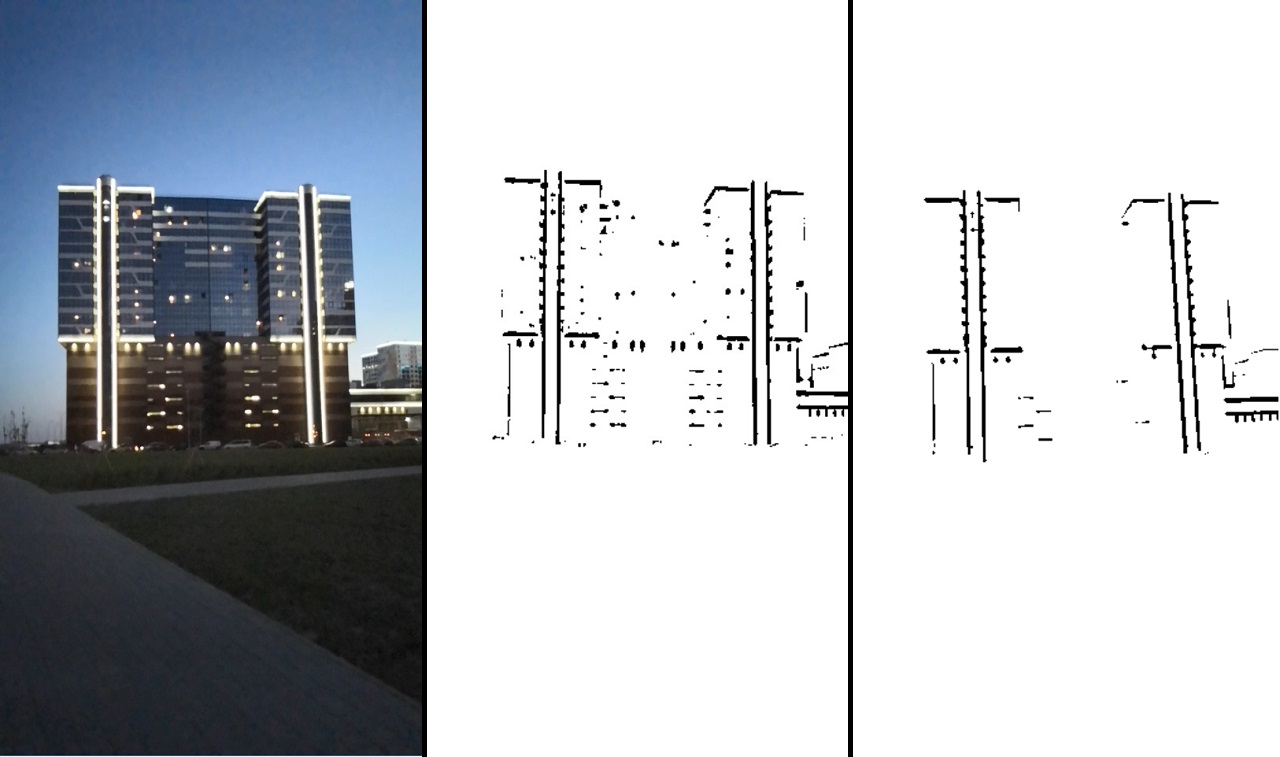
باستمرار: الصورة الأصلية -> بعد تحول العتبة -> بعد التصفية.

هذه الصورة بالفعل تخبرنا بوضوح أين توجد الحافة اليمنى وأين لا توجد. بعد ذلك ، نستخدم الدالة distanceTransform ، ونتيجة لذلك ، سيكون لدينا معلومات حول مدى بعد كل نقطة عن الحافة. تتم الإشارة إلى الصورة الناتجة كـ .

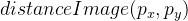
هكذا يبدو الأمر إذا تم تطبيعه وتصوره:



بعد ذلك ، سنحتاج إلى بعض الأدوات الرياضية.

وظيفة الأمثل خوارزمية

تحسين الوظيفة هو مهمة إيجاد الحد الأدنى من الوظيفة.

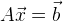
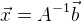
إذا كنا نتعامل مع نظام خطي من المعادلات ، فإن إيجاد الحد الأدنى أمر بسيط للغاية. تخيل نظام المعادلات في شكل مصفوفة: ثم حلنا: . إذا كان لدينا نظام معادلات مفرط التحديد ، فيمكننا استخدام طريقة المربعات الصغرى : .

إذا كانت وظيفتنا غير خطية ، فإن المهمة تصبح أكثر تعقيدًا. للعثور على الحد الأدنى ، يمكنك استخدام خوارزمية Gauss-Newton . الخوارزمية تعمل على النحو التالي:

1. من المفترض أن لدينا بالفعل بعض التقريب الأولي للحل التي سنقوم صقلها بشكل متكرر.
2. باستخدام توسيع تايلور ، يمكننا تقريب خطنا غير الخطية لوظيفة عند نقطة التقريب الحالية. نقوم بحل نظام المعادلات الخطية الناتج بطريقة المربعات الصغرى ، الحصول عليها 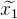. نتيجة لذلك ، لن يكون الحل الناتج حلاً ، ولكنه سيكون أقرب من التقريب الحالي.
3. استبدال التقريب الحالي تلقى القرار 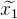وانتقل إلى الخطوة 2. كرر ذلك حتى الفرق بين و لن يكون أقل من قيمة معينة.

دعنا نحلل الخوارزمية بمزيد من التفاصيل.

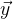
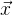
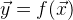
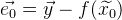
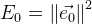
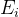
سمح - وظيفة العمل ، - متجه معروف سابقا لقيم الوظيفة. مع الحل الأمثل للمعادلة البيان التالي صحيح . ولكن لدينا فقط تقريبه . ثم يتم الإشارة إلى متجه الخطأ من هذا التقريب كـ: . خطأ عام في الوظيفة سيكون: . الآن العثور على مثل هذا في أي سوف تصل إلى الحد الأدنى ، وسوف نحصل على تقريب أفضل من الحل .
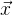
بدءا من النهج سوف نقترب منه بشكل تكراري ، ونحصل على كل تكرار . للقيام بذلك ، نحتاج إلى كل تكرار لحساب مصفوفة Jacobi للوظيفة للتقريب الحالي ، الذي يتكون من مشتقات وظيفتنا:

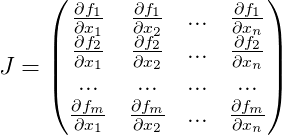
ويرد تقريب التالية على النحو التالي: .
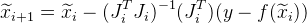
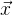
غالبًا ما يتم إنشاء المهام بطريقة تجعل لدينا عددًا كبيرًا من البيانات مستقلة عن بعضها البعض (فقط من القيم ). ونتيجة لذلك ، فإن مصفوفة جاكوبي العامة قليلة للغاية. هناك طريقة لتحسين العمليات الحسابية.
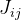
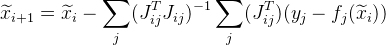
افترض أنه يتم حساب وظيفة شائعة من مجموعة من النقاط. من النقطة jth نحصل عليها . بدلا من حساب مصفوفة جاكوبي للوظيفة بأكملها ، نحسب مصفوفة جاكوبي خصيصا ل ويشار إليها كـ: . بعد ذلك سيتم تقديم التقريب التالي على النحو التالي: . بالإضافة إلى ذلك ، يسمح لك هذا التغيير بموازنة الحسابات.
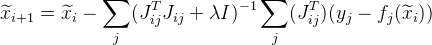
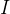
قد يحدث أن القيمة التالية سيعطي خطأ أكبر من . لحل هذه المشكلة ، يمكنك استخدام تعديل الخوارزمية - خوارزمية Levenberg-Marquardt . أضف قيمة في صيغتنا: حيث هي مصفوفة وحدة. قيمة مختارة على النحو التالي:

• أولاً ، لها قيمة صغيرة إلى حد ما (بحيث تتقارب الخوارزمية) ؛
• ثم إذا كان خطأ ل اكثر من ، ثم قم بزيادة القيمة ومحاولة حساب الخطأ ل مرة أخرى.

وأكثر غير الخطية وظيفة كلما كانت القيمة أكبر . ومع ذلك كلما زادت القيمة ، أبطأ الخوارزمية تتلاقى.

نكمل الخوارزمية عندما يختلف عن صغيرة بما يكفي واتخاذ كحل

الخوارزمية عالمية تمامًا ويمكن استخدامها لمجموعة متنوعة من المهام.

نموذج تتبع رياضي

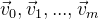
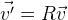
نظرًا لأننا نتعامل مع الإحداثيات في الفضاء ، فمن الواضح أننا بحاجة إلى أن نكون قادرين على التعامل مع هذه الإحداثيات. لنفترض أن لدينا بعض النقاط . ونحن بحاجة إلى تدويرها حول نقطة الصفر مع إحداثيات. ربما تكون أسهل طريقة هي استخدام مصفوفة الدوران R ، التي تصف الدوران الضروري: . إذا احتجنا إلى تغيير النقاط ، فقم فقط بإضافة الموجه المطلوب t : .
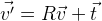
وبالتالي ، يمكنك تغيير موضع كائن ما بشكل تعسفي. اتضح أن إحداثيات الكائن تحددها المصفوفة ثلاثية الأبعاد R والناقل ثلاثي الأبعاد t ، أي 12 معلمات. علاوة على ذلك ، هذه المعلمات ليست مستقلة عن بعضها البعض ، ومكونات مصفوفة التناوب مترابطة بشروط معينة. لذلك ، من وجهة نظر استخدام هذه الوظائف في التحسين ، هذه المعلمات ليست هي الحل الأفضل. هناك معايير أكثر من درجات الحرية ، هناك علاقة بينهما. هناك شكل آخر من أشكال التناوب - صيغة دوران رودريج . يتم تحديد هذا التناوب بواسطة ثلاثة معلمات ، والتي تشكل متجهًا ثلاثي الأبعاد.

المتجه الطبيعي هو محور الدوران ، وطول المتجه هو زاوية الدوران حول هذا المحور.

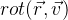
وضعنا وظيفة الدوران للمتجه الخامس : باستخدام المعلمات r لصيغة رودريج. نحصل على الصيغة التالية من هذا: .
وفي النهاية ، يمكننا ضبط إحداثيات موضع الكائن باستخدام متجه ثلاثي الأبعاد:
نحصل على الصيغة التالية: .

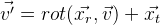
نموذج الكاميرا الثقب

الآن وصفنا نموذجًا رياضيًا بسيطًا للكاميرا المستخدمة في المشروع:

$$

$$\ vec {p} = \ start {pmatrix} p_x & p_y \ end {pmatrix} ^ T = cam (\ vec {v}) = \ start {pmatrix} f_x \ frac {v_x} {v_z} + c_x & f_y \ frac {v_y} {v_z} + c_y \ end {pmatrix} ^ T$$

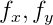
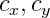
حيث - المسافة البؤرية بالبكسل ؛ - المركز البصري هو أيضا في بكسل. هذه هي معلمات الكاميرا الفردية ، والتي تسمى المعلمات الجوهرية للكاميرا. عادة ، هذه المعلمات معروفة مقدما. في هذا المشروع ، يتم اختيار هذه المعلمات عن طريق العين.

هذا النموذج لا يأخذ في الاعتبار تشويه عدسة الكاميرات ( تشويه ). لنفترض أنهم ليسوا كذلك.

من خلال هذا النموذج ، نحصل على عرض مركزي ، جميع نقاطه تميل أكثر نحو المركز البصري ، أبعد ما يكون عن الكاميرا. وبالتالي نحصل على تأثير السكك الحديدية الضيقة:



في الفضاء ، يتم محاذاة الكاميرا مع المحور z ، ومستوى الصورة موازي للمستوى س ص . نحن نكمل نموذجنا بالقدرة على التحرك في الفضاء:

$$

$$\ vec {p} _j = cam (rot (\ vec {x} _r ، \ vec {v} _j) + \ vec {x} _t)$$

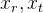
وبالتالي ، حصلنا على نموذج يمكننا به في شكل جبري محاكاة إسقاط نقاط من العالم الخارجي على صورة الكاميرا (من إحداثيات العالم إلى الشاشة). بالنسبة لنا ، تظل معلمات الموضع النسبي للكاميرا في الفضاء غير معروفة في هذا النموذج. . وتسمى هذه المعلمات المعلمات الخارجية للكاميرا.

تتبع

نفذت بالفعل دون أدوات OpenCV. أولاً ، نحتاج إلى الحصول على وظيفة الخطأ لحلنا التقريبي ، الذي تم وصفه أعلاه. وسوف نكتب حسابه على مراحل:

1. نختار حواف نموذج التتبع هذه المرئية استنادًا إلى معلمات التقريب الحالي.
2. نحول مجموعة الحواف المحددة إلى مجموعة ثابتة من النقاط ، لتبسيط العمليات الحسابية. من الممكن ، على سبيل المثال ، أخذ العدد التاسع من النقاط من كل حافة ، أو (خيار أكثر صحة) لاختيار هذه الكمية بحيث تكون هناك مسافة ثابتة بالبكسل بين النقاط. سوف نسميهم نقاط التحكم (في المشروع: controlPoint - نقاط التحكم و controlPixelDistance - نفس المسافة الثابتة بالبكسل).
3. نحن نتوقع نقاط مراقبة على الصورة. بفضل المسافة ، يمكننا الحصول على مسافة إسقاط نقطة التحكم إلى الحافة في الصورة. في الحالة المثالية ، يجب أن تكون جميع نقاط التحكم ملزمة تمامًا على حواف الصورة ، أي يجب أن تكون المسافة إلى الضلع صفر. بناءً على ذلك ، حصلنا على خطأ في نقطة تحكم محددة: .
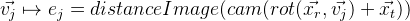4. نحصل على وظيفة الخطأ التالية:

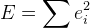
الآن يبقى العثور على الحد الأدنى من E. للقيام بذلك ، نستخدم خوارزمية Levenberg-Marquardt الموضحة أعلاه. كما نعلم بالفعل ، تتطلب الخوارزمية حساب مصفوفة جاكوبي ، أي وظائف مشتقة. يمكنك استخدام الاكتشاف العددي للمشتقات. يمكنك أيضًا استخدام بعض الحلول الجاهزة لهذه الخوارزمية. ومع ذلك ، في هذا المشروع تم كتابة كل شيء يدويًا ، لذلك سوف أصف الاستنتاج الكامل للحل الكامل.

لكل نقطة تحكم ، نحصل على معادلة مستقلة عن النقاط الأخرى. لقد سبق وصفنا أعلاه أنه في هذه الحالة من الممكن النظر في هذه المعادلات بشكل مستقل عن بعضها البعض ، بحساب مصفوفة جاكوبي لكل منها على حدة. سنقوم بتحليلها بالترتيب ، باستخدام قواعد التمايز لوظيفة معقدة:



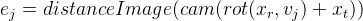
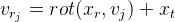
نحن نشير ثم



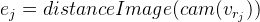
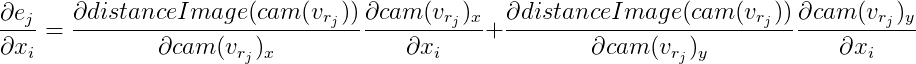
من هنا:



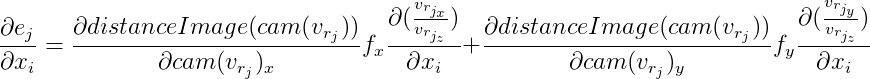
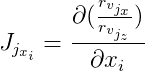
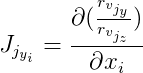
كذلك نشير و ثم:


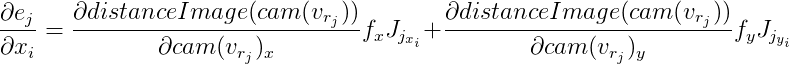
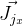
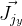
مشتقات المسافة هي عدديا. وللحوسبة ناقلات و ستحتاج إلى العثور على المشتقات وفقًا لتدوير رودريج. لقد وجدت Jacobian بهذه الصيغة في المنشور "صيغة مضغوطة لمشتق دوران ثلاثي الأبعاد في
الإحداثيات الأسية »غييرمو غاليغو ، أنتوني يزي :

.
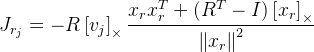
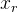
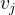
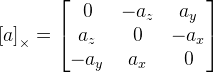
حيث R هي مصفوفة الدوران التي حصلت عليها صيغة رودريغ من متجه الدوران . - النقطة التي نتحول ؛ أنا مصفوفة الهوية ؛ . كما نرى هنا ، لدينا تقسيم على طول متجه التناوب ، وإذا كان المتجه صفراً ، فإن الصيغة لم تعد تعمل. ربما يرجع هذا إلى حقيقة أن محور الدوران عند الصفر المتجه غير معرف. إذا كان ناقل التدوير قريبًا جدًا من الصفر ، فإننا نستخدم هذه الصيغة: .
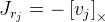
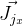
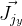
يبقى أن ترسم و ( تم حذف الفهرس j هنا):


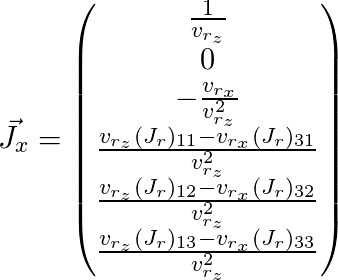
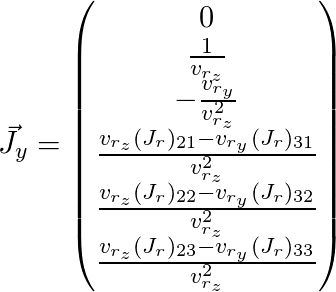
وبالتالي ، حصلنا على مصفوفة Jacobi للنقطة التي نحتاجها ويمكننا استخدامها لخوارزمية التحسين الموضحة أعلاه.

هناك العديد من المشاكل مع هذه الخوارزمية. أولا ، الدقة. نتيجة لذلك ، ينتقل الوضع العالمي للكاميرا قليلاً من إطار إلى إطار. يمكنك اصلاحها قليلا. لدينا معلومات مسبقة تفيد بأن موضع الكاميرا لا يمكن أن يتغير بشكل كبير من إطار إلى آخر. ويمكننا تقليل هذا الارتعاش من خلال إضافة معادلات إضافية إلى الوظيفة.

يجب أن نتذكر أن ناقل الإزاحة t ليس في حالتنا هو إحداثيات الموقع العالمي للكاميرا. الموضع العالمي هو نقطة محلية بإحداثيات صفرية ، لذلك يمكن اشتقاقها على النحو التالي:



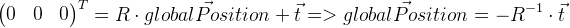
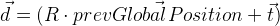
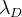
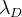
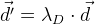
نتذكر موقف الإطار السابق في prevGlobalPosition . الآن ، يجب أن يكون الموضع السابق قريبًا من الصفر ، أي طول المتجه يجب أن تكون صغيرة بما فيه الكفاية. أي إلى جانب القيم الأخرى للتناقضات ، يجب أيضًا تقليل المتجه d . لتحديد درجة تأثير هذا التعديل ، نقدم القيمة واضرب المتجه d ب اضافة ب : . أي في خوارزمية التحسين ، نقوم أيضًا بتقليل المتجه d ' . بالطبع ، لهذا سيكون من الضروري حساب مصفوفة Jacobi لها ، والتي تم اشتقاقها بنفس الطريقة التي اشتقناها من قبل لوظيفة الخطأ العامة.

المشكلة الثانية من الخوارزمية هي أنه يمكن أن تتعثر في الحد الأدنى المحلي. في أعمال أخرى ، يتم حل هذه المشكلة باستخدام مرشح الجسيمات. في حالتنا ، اتضح أن هذا الخيار كافٍ من حيث المبدأ.

مكافآت من تتبع كائن

معرفة موقع وشكل الكائن ، يمكنك التعامل معهم بصريا ، والتي حاولت أن أظهر على الفيديو. تم تشويه الكائن باستخدام تظليل OpenGL. بمساعدة نموذجنا ، قمت بإسقاط نقطة الكائن على الصورة ، وبالتالي تلقيت لون هذه النقطة. ثم يمكنك تحريك هذه النقطة ، والحصول على تأثيرات مثيرة للاهتمام - على سبيل المثال ، تتحول. ومع ذلك ، يجب على المرء أن يتذكر أن تغيير النقطة ، من الضروري أن يبقى شيء ما في مكانه ، وإلا ستصبح التناقضات ملحوظة. بالإضافة إلى ذلك ، وفقًا لجودة التتبع وشكل الكائن ، سوف نتلقى العديد من الآثار غير المرغوب فيها بسبب الأخطاء المتراكمة ، والتي ستظل كذلك. يحتاج فقط أن تؤخذ بعين الاعتبار بطريقة أو بأخرى. في الفيديو المقدم أعلاه ، أردت أن أظهر أنه يمكن استخدام الواقع المعزز أوسع قليلاً من مجرد فرض كائنات افتراضية على الصورة.

بالمناسبة ، تطبق Vuforia SDK تتبع كائن ما من خلال شكله ، على الرغم من أنني لا أعتقد أنه سيكون من الممكن تنفيذ هذا المشروع معه ، لأنه لا يمكن استخدام حواف محددة بدقة ولا يمكن ربطه بإضاءة المبنى.