متى يستحق التحقق من فرضية لا تقل فعالية؟

تقترح مقالة من فريق Stitch Fix استخدام نهج البحث السريري للتجارب غير الدونية في اختبارات التسويق والمنتجات A / B. هذا النهج قابل للتطبيق حقًا عندما نختبر حلاً جديدًا له مزايا لا يمكن قياسها عن طريق الاختبارات.

أبسط مثال هو فقدان العظام. على سبيل المثال ، نقوم تلقائيًا بعملية تعيين الدرس الأول ، لكننا لا نريد أن نتجاوز عملية التحويل كثيرًا. أو نختبر التغييرات التي تركز على شريحة واحدة من المستخدمين ، مع التأكد من أن التحويلات عبر القطاعات الأخرى لا تغرق كثيرًا (عند اختبار العديد من الفرضيات ، لا تنسَ التصحيحات).

ويضيف اختيار الحد الصحيح الذي لا يقل كفاءة عن ذلك صعوبات إضافية في مرحلة تصميم الاختبار. مسألة كيفية اختيار question في المقال لم يتم الكشف عنها بشكل جيد. يبدو أن هذا الاختيار ليس شفافًا تمامًا في التجارب السريرية. تشير مراجعة المنشورات الطبية حول عدم الدونية إلى أن اختيار الحدود في نصف المنشورات فقط له ما يبرره وغالبًا ما تكون هذه التبريرات غامضة أو غير مفصلة.

في أي حال ، هذا النهج يبدو مثيرا للاهتمام ، ل عن طريق تقليل حجم العينة المطلوب ، يمكن أن تزيد من سرعة الاختبار ، وبالتالي سرعة صنع القرار. - داريا موخينا ، محللة المنتج لتطبيق Skyeng للهاتف المحمول.

يحب فريق Stitch Fix اختبار أشياء مختلفة. مجتمع التكنولوجيا بأكمله ، من حيث المبدأ ، يحب إجراء الاختبارات. أي إصدار من الموقع يجذب المزيد من المستخدمين - A أو B؟ هل تجلب النسخة A من نموذج التوصية أموالًا أكثر من الإصدار B؟ دائمًا تقريبًا ، لاختبار الفرضيات ، نستخدم الطريقة الأبسط من دورة الإحصاء الأساسية:



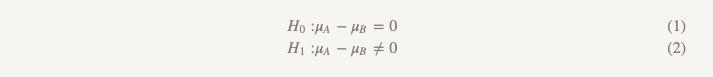
على الرغم من أننا نادراً ما نستخدم هذا المصطلح ، فإن هذا النوع من الاختبارات يسمى "فرضية اختبار التفوق". مع هذا النهج ، نفترض أنه لا يوجد فرق بين الخيارين. نحن نتمسك بهذه الفكرة ونرفضها فقط إذا كانت البيانات التي تم الحصول عليها مقنعة بما يكفي لهذا - أي أنها توضح أن أحد الخيارات (A أو B) أفضل من الآخر.

يعتبر اختبار فرضية التفوق مناسبًا لحل العديد من المشكلات. نقوم بإصدار الإصدار B من نموذج التوصية فقط إذا كان أفضل من الإصدار المستخدم بالفعل بشكل واضح. ولكن في بعض الحالات ، لا يعمل هذا النهج أيضًا. دعونا نلقي نظرة على بعض الأمثلة.

1) نستخدم خدمة جهة خارجية تساعد في تحديد البطاقات المصرفية المزيفة. وجدنا خدمة أخرى تكلف أقل بكثير. إذا كانت خدمة أرخص تعمل وكذلك الخدمة التي نستخدمها الآن ، فسنختارها. ليس من الضروري أن يكون أفضل من الخدمة المستخدمة.

2) نريد التخلي عن مصدر البيانات A واستبداله بمصدر البيانات B. قد نتأخر في التخلي عن A إذا كانت B تعطي نتائج سيئة للغاية ، لكن لا يمكن الاستمرار في استخدام A.

3) نود أن ننتقل من النهج إلى النمذجة A إلى النهج B ليس لأننا نتوقع نتائج أفضل من B ، ولكن لأنها تتيح لنا مرونة تشغيلية كبيرة. ليس لدينا أي سبب للاعتقاد بأن B سيكون أسوأ ، لكننا لن نبدأ الانتقال إذا كان هذا هو الحال.

4) لقد أجرينا العديد من التغييرات النوعية على تصميم موقع الويب (الإصدار B) ونعتقد أن هذا الإصدار أفضل من الإصدار A. لا نتوقع حدوث تغييرات في التحويل أو أي مؤشرات أداء رئيسية نقوم عادةً بتقييمها على الموقع. لكننا نعتقد أن هناك مزايا في المعايير التي لا يمكن قياسها ، أو أن تقنياتنا ليست كافية للقياس.

في كل هذه الحالات ، فإن البحث عن التميز ليس هو الحل الأفضل. لكن معظم الخبراء في هذه الحالات يستخدمونه افتراضيًا. نجري تجربة بعناية لتحديد حجم التأثير بشكل صحيح. إذا كان صحيحًا أن الإصدارات A و B تعمل بشكل مشابه جدًا ، فهناك فرصة ألا نتمكن من رفض الفرضية الفارغة. هل نستنتج أن A و B يعملان بشكل عام؟ لا! عدم القدرة على رفض الفرضية الفارغة واعتماد الفرضية الفارغة ليسا نفس الشيء.

عادة ما يتم إجراء حسابات حجم العينة (التي قمت بها ، بالطبع) بحدود أكثر صرامة للخطأ الأول (احتمال الرفض الخاطئ للفرضية الفارغة ، وغالبًا ما يطلق عليها ألفا) من الخطأ النوع الثاني (احتمال الفشل في رفض الفرضية الفارغة ، عندما بافتراض أن الفرضية الخاطئة خاطئة ، وغالبًا ما تسمى التجريبية) القيمة النموذجية لـ alpha هي 0.05 ، في حين أن القيمة النموذجية للبيتا هي 0.20 ، والتي تتوافق مع قوة إحصائية قدرها 0.80. هذا يعني أنه مع أننا لا نستطيع اكتشاف التأثير الحقيقي للقيمة التي أشرنا إليها في حسابات الطاقة لدينا مع احتمال بنسبة 20 ٪ وهذه فجوة معلومات خطيرة إلى حد ما. كمثال ، دعنا نفكر في الفرضيات التالية:



H0: حقيبتي ليست في غرفتي (3)
H1: حقيبتي في غرفتي (4)

إذا قمت بالبحث في غرفتي ووجدت حقيبتي على ما يرام - يمكنني رفض فرضية لاغية. لكن إذا نظرت حول الغرفة ولم أتمكن من العثور على حقيبتي (الشكل 1) ، فما هي النتيجة التي يجب أن أستخلصها؟ هل أنا متأكد من أنه ليس هناك؟ لقد بحثت جيدا بما فيه الكفاية؟ ماذا لو بحثت عن 80٪ فقط من الغرفة؟ لاستنتاج أن حقيبة الظهر ليست بالتأكيد في الغرفة سيكون قرارًا سريعًا. ليس من المستغرب ، لا يمكننا "قبول الفرضية الفارغة".

المنطقة بحثنا
لم نجد حقيبة ظهر - فهل يجب علينا قبول الفرضية الفارغة؟

الشكل 1. البحث عن 80 ٪ من الغرفة هو نفسه تقريبا عند إجراء دراسة بسعة 80 ٪. إذا لم تجد حقيبة ظهر ، بعد أن فحصت 80٪ من الغرفة ، هل من الممكن أن نستنتج أنها ليست موجودة؟

إذن ما الذي يفعله متخصص البيانات في هذا الموقف؟ يمكنك زيادة الطاقة البحثية بشكل كبير ، ولكن بعد ذلك ستحتاج إلى عينة أكبر بكثير ، وستظل النتيجة غير مرضية.

لحسن الحظ ، تمت دراسة هذه المشاكل منذ فترة طويلة في عالم الأبحاث السريرية. المخدرات B أرخص من المخدرات A ؛ المخدرات B من المتوقع أن يسبب آثار جانبية أقل من المخدرات A ؛ المخدرات B أسهل في النقل لأنه لا يحتاج إلى تخزينها في الثلاجة ، وهناك حاجة إلى المخدرات A. نحن اختبار فرضية لا تقل الكفاءة. يعد ذلك ضروريًا لإظهار أن النسخة B جيدة مثل الإصدار A - على الأقل ضمن حد معين محدد مسبقًا وهو "لا تقل كفاءة" ، Δ. بعد ذلك بقليل سنتحدث أكثر عن كيفية تعيين هذا الحد. لكن لنفترض الآن أن هذا هو الفرق الأصغر الذي له أهمية عملية (في سياق التجارب السريرية ، يُسمى هذا عادةً الصلة السريرية).

فرضيات لا تقل الكفاءة تقلب كل شيء رأسًا على عقب:



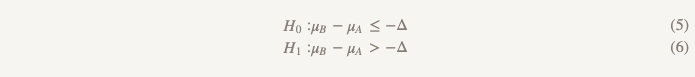
الآن ، بدلاً من افتراض عدم وجود فرق ، نفترض أن الإصدار B أسوأ من الإصدار A ، وسوف نتمسك بهذا الافتراض حتى نثبت أنه ليس كذلك. هذه هي بالضبط اللحظة التي يكون فيها من المنطقي استخدام اختبار فرضية من جانب واحد! في الممارسة العملية ، يمكن القيام بذلك عن طريق بناء فاصل الثقة وتحديد ما إذا كان الفاصل الزمني أكبر بالفعل من Δ (الشكل 2).

Δ الاختيار

كيف تختار Δ؟ تشتمل عملية الاختيار statistical على مبرر إحصائي وتقييم للموضوع. هناك توصيات معيارية في عالم التجارب السريرية ، والتي تتبع أن الدلتا يجب أن تكون أصغر فرق مهم سريريًا - واحد سيكون ذا صلة في الممارسة. فيما يلي اقتباس من القيادة الأوروبية ، يمكنك من خلاله التحقق من نفسك: "إذا تم اختيار الفرق بشكل صحيح ، فستكون فاصل الثقة الذي يقع تمامًا بين ∆ و 0 ... لا يكفي لإظهار كفاءة أقل. إذا كانت هذه النتيجة غير مقبولة ، فهذا يعني أن "لم يتم اختياره بشكل مناسب".

يجب ألا تتجاوز دلتا حجم التأثير في الإصدار A فيما يتعلق بالتحكم الحقيقي (الغفل / عدم العلاج) ، لأن هذا يقودنا إلى الاعتقاد بأن الإصدار B أسوأ من التحكم الحقيقي وفي الوقت نفسه يوضح "لا تقل الكفاءة". لنفترض أنه عند تقديم الإصدار A ، كان الإصدار 0 في مكانه أو أن الوظيفة لم تكن موجودة على الإطلاق (انظر الشكل 3).

استنادًا إلى نتائج اختبار فرضية التفوق ، تم الكشف عن حجم التأثير E (أي ، من المفترض μ ^ A - 0 ^ 0 = E). الآن A هو المعيار الجديد لدينا ، ونريد التأكد من أن B ليست أدنى من A. وهناك طريقة أخرى لكتابة μB - μA≤ - Δ (فرضية فارغة) هي μB≤μA - Δ. إذا افترضنا أن الفعل يساوي أو يزيد عن E ، فعندئذٍ μB ≤ μA - E ≤ وهمي. الآن نرى أن تقديرنا لـ μB يتجاوز تمامًا μA - E ، والذي يدحض تمامًا الفرضية الفارغة ويسمح لنا أن نستنتج أن B ليست أدنى من A ، ولكن في الوقت نفسه ، قد تكون ≤B μ وهميًا ، ولكن هذا ليس صحيحًا ماذا نحتاج (الشكل 3).


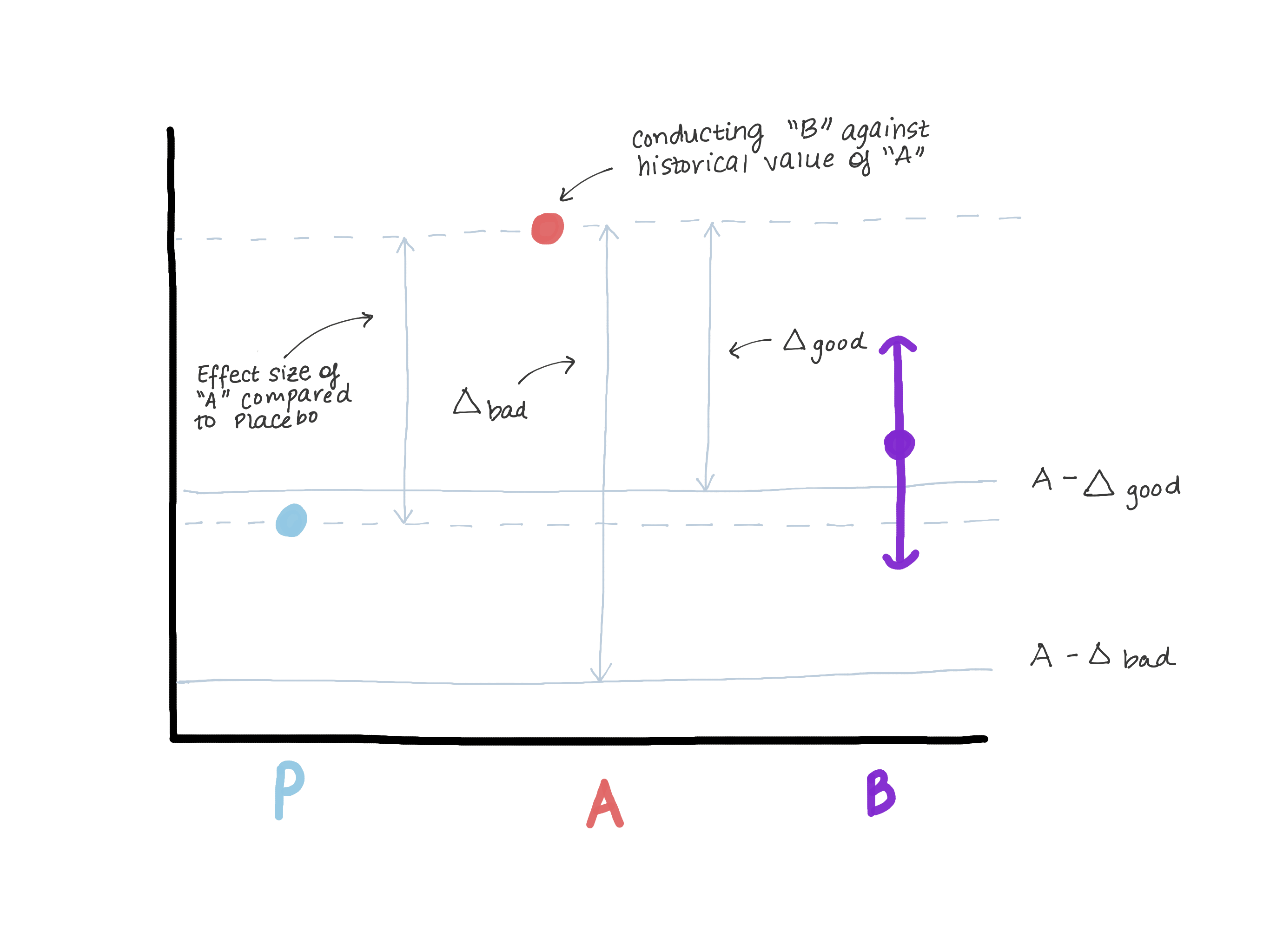الشكل 3. إظهار مخاطر اختيار حد لا يقل كفاءة. إذا كان الحد كبيرًا جدًا ، فيمكننا أن نستنتج أن B ليس أدنى من A ، ولكن في نفس الوقت لا يمكن تمييزه عن العقار الوهمي. لن نقوم بتغيير الدواء ، والذي من الواضح أنه أكثر فعالية من الدواء الوهمي (A) ، على الدواء ، الذي له نفس فعالية الدواء الوهمي.

اختيار α

نمر إلى اختيار α. يمكنك استخدام القيمة القياسية α = 0.05 ، لكن هذا ليس صادقًا تمامًا. على سبيل المثال ، عندما تشتري شيئًا ما على الإنترنت وتستخدم عدة رموز للخصم في آنٍ واحد ، على الرغم من أنه لا ينبغي تلخيصها ، فقد ارتكب المطور خطأً وتخلصت منه. وفقًا للقواعد ، يجب أن تكون قيمة α مساوية لنصف قيمة α ، والتي تُستخدم لاختبار فرضية التفوق ، أي 0.05 / 2 = 0.025.

حجم العينة

كيفية تقدير حجم العينة؟ إذا كنت تعتقد أن متوسط ​​الفرق الحقيقي بين A و B هو 0 ، فسيكون حساب حجم العينة هو نفسه عند اختبار فرضية التفوق ، باستثناء أنك تستبدل حجم التأثير بحد لا يقل كفاءة ، بشرط استخدام α لا تقل الكفاءة = 1/2 التفوق (αnon - الدونية = 1/2 متفوقة). إذا كان لديك سبب للاعتقاد بأن الخيار "ب" قد يكون أسوأ قليلاً من الخيار "أ" ، لكنك تريد أن تثبت أنه أسوأ بما لا يزيد عن Δ ، فأنت محظوظ! في الواقع ، هذا يقلل من حجم عينتك ، لأنه من الأسهل إثبات أن B أسوأ من A إذا كنت تعتقد حقًا أنها أسوأ قليلاً وغير متكافئة.

مثال الحل

افترض أنك تريد الترقية إلى الإصدار B شريطة أن يكون أسوأ من الإصدار A بما لا يزيد عن 0.1 نقطة بمقياس رضا العملاء المكون من 5 نقاط ... سنتعامل مع هذه المهمة باستخدام فرضية التفوق.

لاختبار فرضية التفوق ، قمنا بحساب حجم العينة على النحو التالي:



أي أنه إذا كان لديك 2103 ملاحظة في مجموعتك ، فيمكنك أن تتأكد بنسبة 90٪ من أنك ستجد تأثيرًا 0.10 أو أكثر. ولكن إذا كانت قيمة 0.10 كبيرة جدًا بالنسبة لك ، فربما لا يجب عليك اختبار فرضية التفوق لها. ربما ، من أجل الموثوقية ، قررت إجراء دراسة بحجم تأثير أصغر ، على سبيل المثال ، 0.05. في هذه الحالة ، ستحتاج إلى 8407 ملاحظة ، أي أن العينة ستزيد حوالي 4 مرات. لكن ماذا لو التزمنا بحجم العينة الأصلي ، لكن زدنا القدرة إلى 0.99 حتى لا نشك في حصولنا على نتيجة إيجابية؟ في هذه الحالة ، سيكون n لمجموعة واحدة 3676 ، وهو أفضل ، ولكنه يزيد من حجم العينة بأكثر من 50٪. ونتيجة لذلك ، لا يمكننا جميعًا دحض الفرضية الفارغة ، ولا نحصل على إجابة لسؤالك.

ماذا لو ، بدلا من ذلك ، نحن اختبار فرضية لا تقل فعالية؟



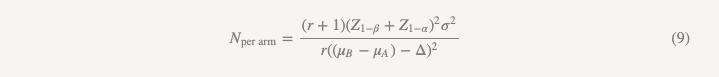
سيتم حساب حجم العينة باستخدام نفس الصيغة باستثناء المقام.
الاختلافات في الصيغة المستخدمة لاختبار فرضية التفوق هي كما يلي:

- يتم استبدال Z1 - α / 2 بـ Z1 - α ، ولكن إذا قمت بكل شيء وفقًا للقواعد ، فستستبدل α = 0.05 بـ α = 0.025 ، وهذا هو نفس الرقم (1.96)

- يظهر في المقام (μB - μA)

- يتم استبدال magn (حجم التأثير) بـ Δ (حد لا يقل الكفاءة)

إذا افترضنا أن µB = µA ، فإن (µB - µA) = 0 وحساب حجم العينة بحد أدنى لا يقل كفاءة هو بالضبط ما سوف نحصل عليه عند حساب التفوق لقيمة التأثير البالغة 0.1 ، عظيم! يمكننا إجراء دراسة على نفس المقياس بفرضيات مختلفة ونهج مختلف للاستنتاجات ، وسنحصل على إجابة للسؤال الذي نريد حقًا الإجابة عليه.

لنفترض الآن أننا لا نعتقد حقًا أن µB = µA و
نعتقد أن µB أسوأ قليلاً ، وربما 0.01 وحدة. هذا يزيد قاسمنا ، مما يقلل من حجم العينة لكل مجموعة إلى 1737.

ماذا يحدث إذا كانت النسخة B أفضل من الإصدار A؟ نحن ندحض الفرضية الفارغة بأن B أسوأ من A بأكثر من Δ ونقبل الفرضية البديلة بأن B ، إذا أسوأ ، ليست أسوأ من Δ ، ويمكن أن تكون أفضل. حاول وضع هذا الاستنتاج في عرض تقديمي متعدد الوظائف وشاهد ما يأتي منه (على محمل الجد ، جرّبه). في موقف تحتاج فيه إلى التركيز على المستقبل ، لا يريد أحد أن يوافق على "ما هو أسوأ من لا أكثر ، وربما أفضل".

في هذه الحالة ، يمكننا إجراء دراسة تسمى باختصار شديد "اختبار الفرضية القائلة بأن أحد الخيارات متفوق على الآخر أو أدنى منه". ويستخدم مجموعتين من الفرضيات:

المجموعة الأولى (كما هو الحال عند اختبار فرضية لا تقل الكفاءة):



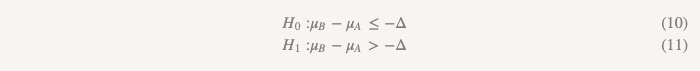
المجموعة الثانية (نفس الشيء عند اختبار فرضية التفوق):



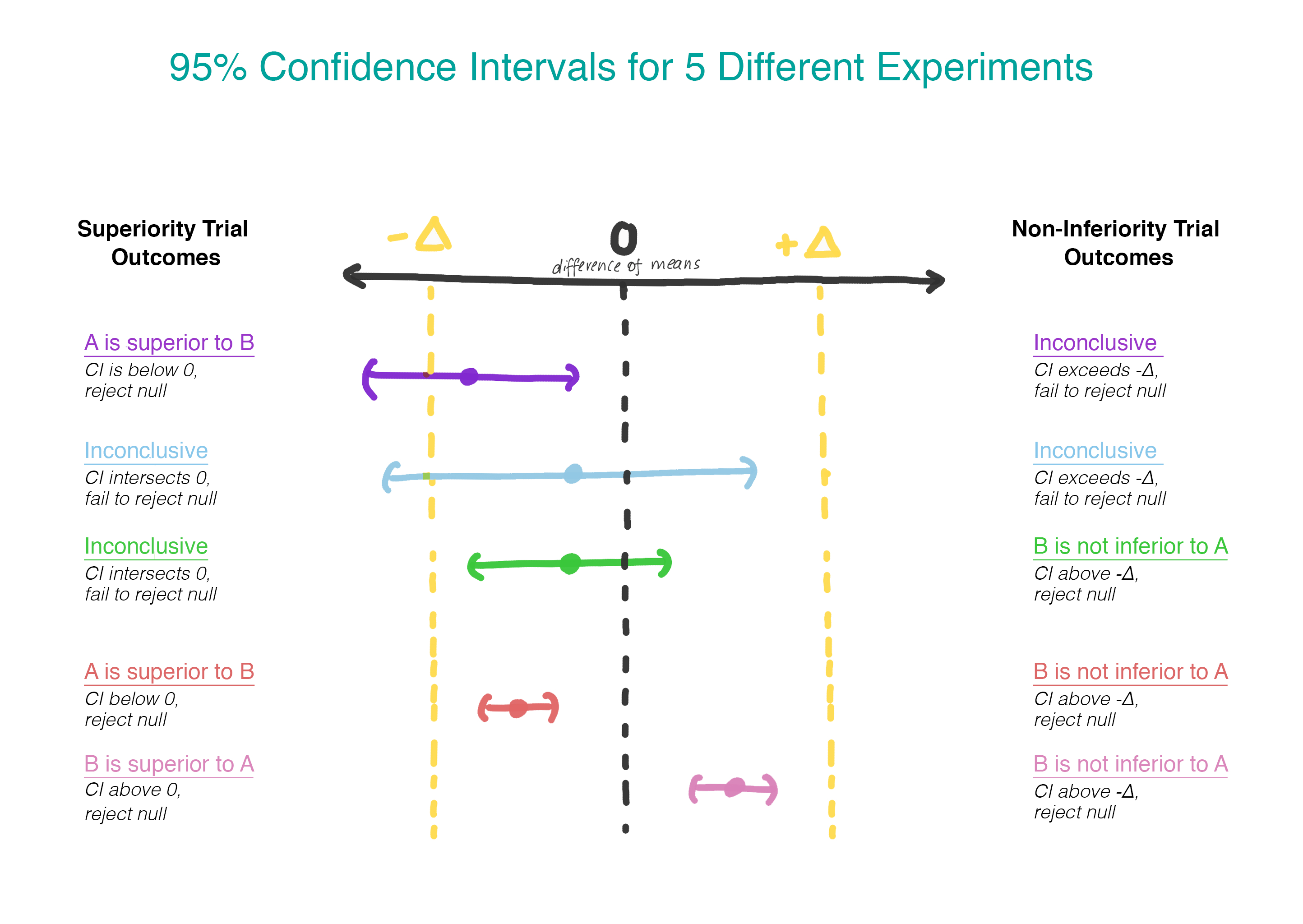
نحن نختبر الفرضية الثانية فقط إذا تم رفض الأولى. في الاختبار المتسلسل ، نحافظ على المستوى العام للأخطاء من النوع الأول (α). في الممارسة العملية ، يمكن تحقيق ذلك عن طريق إنشاء فاصل ثقة 95 ٪ للفرق بين الوسائل والتحقق لتحديد ما إذا كان الفاصل الزمني بأكمله يتجاوز -Δ. إذا لم تتجاوز الفترة الزمنية - Δ ، فلا يمكننا رفض القيمة الصفرية والتوقف. إذا كان الفاصل الزمني بأكمله يتجاوز بالفعل −Δ ، سنواصل ونرى ما إذا كان الفاصل الزمني يحتوي على 0.

هناك نوع آخر من الأبحاث لم نناقشه - دراسات التكافؤ.

يمكن استبدال الدراسات من هذا النوع بدراسات لاختبار فرضية لا تقل فاعلية والعكس صحيح ، ولكن في الواقع يوجد اختلاف مهم بينهما. يهدف اختبار لاختبار فرضية لا تقل كفاءة إلى إظهار أن الخيار B جيد على الأقل مثل A. ودراسة التكافؤ تهدف إلى إظهار أن الخيار B جيد على الأقل مثل A ، و الخيار A جيد مثل B ، وهو أكثر تعقيدًا. في جوهرها ، نحن نحاول تحديد ما إذا كان الفاصل الزمني الثقة بأكمله يكمن في الفرق بين means و Δ. مثل هذه الدراسات تتطلب حجم عينة أكبر وأقل تواترا. لذلك ، في المرة القادمة التي تجري فيها دراسة تكون مهمتك الرئيسية فيها هي التأكد من أن الإصدار الجديد ليس أسوأ ، لا تقبل "عدم القدرة على دحض الفرضية الفارغة". إذا كنت ترغب في اختبار فرضية مهمة حقًا ، ففكر في العديد من الخيارات.