كتاب "التعلم الآلي: الخوارزميات للأعمال"

مرحبا ، habrozhiteli! يشارك ماركوس لوبيز دي برادو ما يخفيه عادة - خوارزميات التعلم الآلي الأكثر ربحية التي استخدمها منذ عقدين لإدارة مجموعات كبيرة من الأموال من المستثمرين الأكثر تطلبا.

يغير التعلم الآلي تقريبًا كل جانب من جوانب حياتنا ؛ تؤدي خوارزميات MO مهامًا لم يكن يثق بها إلا خبراء موثوقون حتى وقت قريب. في المستقبل القريب ، سيهيمن التعليم الآلي على التمويل ، وسيكون سرد الثروة شيئًا من الماضي ، ولن تعد الاستثمارات مرادفة للمقامرة.

انتهز الفرصة للمشاركة في "ثورة الآلة" ، لذلك يكفي التعرف على الكتاب الأول الذي يقدم تحليلًا كاملًا ومنهجيًا لأساليب التعلم الآلي فيما يتعلق بالتمويل: البدء بهياكل البيانات المالية ، ووضع علامة على السلسلة المالية ، ووزن العينة ، والتمييز بين السلاسل الزمنية ... وتنتهي بـ الجزء كله مخصص ل backtesting الصحيح لاستراتيجيات الاستثمار.

مقتطفات. فهم استراتيجيات المخاطر

15.1. موضوعية

غالبًا ما يتم تنفيذ استراتيجيات الاستثمار من حيث المناصب التي يتم الاحتفاظ بها حتى يتم استيفاء أحد الشرطين: 1) شرط ترك المركز مع الأرباح (جني الأرباح) أو 2) شرط ترك المركز مع الخسائر (إيقاف الخسارة). حتى عندما لا تعلن الاستراتيجية صراحةً عن وقف الخسارة ، يوجد دائمًا حد وقف الخسارة الضمني الذي لم يعد بإمكان المستثمر تمويله من خلال مركزه (نداء الهامش) أو تكبده ضرر ناتج عن زيادة الخسارة غير المحققة. نظرًا لأن معظم الاستراتيجيات لها (صراحة أو ضمنيًا) هذين الشرطين للخروج ، فمن المنطقي أن تصمم توزيع النتائج من خلال عملية ذات الحدين. وهذا بدوره سيساعدنا على فهم أي مجموعات من معدلات المراهنات والمخاطر والدفعات غير اقتصادية. الغرض من هذا الفصل هو مساعدتك في تقييم متى تكون الإستراتيجية عرضة للتغييرات الصغيرة في أي من هذه الكميات.

ضع في اعتبارك استراتيجية تنتج n رهانات متوازنة وموزعة بشكل متبادل كل عام ، حيث تكون النتيجة Xi للرهان i ∈ [1، n] هي الربح π> 0 مع الاحتمال P [Xi = π] = p والخسارة –π مع الاحتمال P [Xi = –Π] = 1 - ص. يمكنك أن تتخيل p على أنها دقة المصنف الثنائي ، حيث تعني النتيجة الإيجابية إنهاء الرهان على الفرصة ، والنتيجة السلبية تعني ضياع الفرصة: يتم مكافأة البيانات الحقيقية ، ومعاقبة البيانات الخاطئة ، والنتائج السلبية (سواء أكانت صحيحة أم خاطئة) ليس لها عوائد. نظرًا لأن نتائج الرهانات {Xi} i = 1 ، ... ، n مستقلة ، فسوف نحسب اللحظات المتوقعة لكل رهان. الربح المتوقع من رهان واحد هو E [Xi] = πp + (–π) (1 - p) = π (2p - 1). 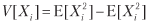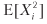الفرق هو حيث = π2p + (–π) 2 (1 - p) = π2 ، وبالتالي ، V [Xi] = π2 - π2 (2p - 1) 2 = π2 [1– (2p - 1) 2] = 4π2p (1 - p ). بالنسبة إلى n الموزعة بالتساوي ، وأسعار مستقلة عن بعضها البعض في السنة ، فإن متوسط ​​نسبة شارب السنوية (θ) هو


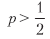
لاحظ كيف π يوازن المعادلة أعلاه لأن الدفعات متماثلة. كما هو الحال في الحالة الغوسية ، يمكن فهم θ [p، n] على أنها قيمة قابلة لإعادة القياس 1. هذا يوضح حقيقة أنه حتى بالنسبة للصغيرة يمكن جعل نسبة شارب عالية ل n كبيرة بما فيه الكفاية. يعد هذا بمثابة الأساس الاقتصادي للتداول عالي التردد ، حيث يمكن أن تكون p أعلى قليلاً من 0.5 ، ومفتاح نشاط التبادل الناجح هو زيادة في n. تعد نسبة Sharpe دالة من الدقة وليست صحيحة ، لأن فقدان فرصة (بيان سلبي) لا يتم مكافأته أو معاقبته بشكل مباشر (على الرغم من أن الكثير من العبارات السلبية يمكن أن تؤدي إلى n صغيرة ، مما يقلل من معامل Sharpe إلى صفر).

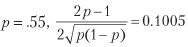
على سبيل المثال ، ل وللوصول إلى متوسط ​​معدل شارب السنوي 2 ، 396 رهانات في السنة مطلوبة. قائمة 15.1 يتحقق من هذه النتيجة تجريبيا. يوضح الشكل 15.1 نسبة Sharpe كدالة للدقة في ترددات الرهان المختلفة.

ادراج 15.1. نسبة شارب كدالة لعدد الرهانات

out,p=[],.55 for i in xrange(1000000): rnd=np.random.binomial(n=1,p=p) x=(1 if rnd==1 else -1) out.append(x) print np.mean(out),np.std(out),np.mean(out)/np.std(out) 

هذه المعادلة تعبر بوضوح تام عن المفاضلة بين الدقة (ع) والتردد (ن) لمعامل شارب معين (θ). على سبيل المثال ، من أجل إعطاء متوسط ​​نسبة شارب سنوي 2 لاستراتيجية تنتج معدلات أسبوعية فقط (ن = 52) ، ستكون هناك حاجة إلى دقة عالية إلى حد ما ع = 0.6336.

15.3. المدفوعات غير المتماثلة

فكر في استراتيجية تنتج n رهانات مستقلة بشكل متبادل موزعة بشكل متماثل في السنة ، حيث تكون النتيجة Xi للرهان i ∈ [1، n] هي π + مع الاحتمال P [Xi = π +] = p ، والنتيجة π– (π– <π + ) يحدث مع الاحتمال P [Xi = π_] = 1 - p. الربح المتوقع من رهان واحد هو E [Xi] = pπ + + (1 - p) π– = (π + - π–) p + π–. التشتت هو V [Xi] = ، حيث



أخيرًا ، يمكننا حل المعادلة السابقة لـ 0 ≤ p ≤ 1 والحصول على


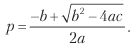
حيث:
a = (n + θ2) (π + - π–) 2؛
b = [2nπ - θ2 (π + - π -)] (π + - π–) ؛


ملاحظة: تتحقق عملية الإدراج 15.2 من هذه العمليات الرمزية باستخدام Python SymPy Live shell التي تعمل على خدمة Google App Engine السحابية: live.sympy.org .

ادراج 15.2. استخدام مكتبة SymPy للعمليات الرمزية

 >>> from sympy import * >>> init_printing(use_unicode=False,wrap_line=False,no_global=True) >>> p,u,d=symbols('pu d') >>> m2=p*u**2+(1-p)*d**2 >>> m1=p*u+(1-p)*d >>> v=m2-m1**2 >>> factor(v) 

المعادلة أعلاه تجيب على السؤال التالي: بالنسبة لقاعدة تداول معينة تتميز بالمعايير {π– ، π + ، n} ، ما درجة الدقة p اللازمة لتحقيق نسبة Sharpe تساوي θ *؟ على سبيل المثال ، من أجل الحصول على θ = 2 لـ n = 260 ، π– = –.01 ، π + = .005 ، نحتاج إلى p = .72. نظرًا للعدد الكبير من الرهانات ، أدى تغيير بسيط جدًا في p (من p = .7 إلى p = .72) إلى تعزيز نسبة Sharpe من 1.1 = 1.173 إلى θ = 2. من ناحية أخرى ، يخبرنا هذا أيضًا أن هذه الاستراتيجية عرضة للصغيرة التغييرات في ص. تطبق القائمة 15.3 اشتقاق الدقة المتوقعة. في التين. 15.2 تُظهر الدقة المفترضة كدالة لـ n و π– ، حيث π + = 0.1 و θ * = 1.5. نظرًا لأن العتبة π– تصبح أكثر سالبة بالنسبة إلى n معين ، يلزم الحصول على درجة p أعلى لتحقيق θ * لعتبة معينة π +. نظرًا لأن العدد n يصبح أصغر بالنسبة إلى عتبة معينة π– ، يلزم الحصول على درجة أعلى من p لتحقيق θ * بالنسبة إلى given +.

ادراج 15.3. حساب الدقة المقدرة

 def binHR(sl,pt,freq,tSR): ´´´ 

بالنسبة لقاعدة تداول معينة تتميز بالمعلمات {sl، pt، freq} ، ما هو الحد الأدنى من الدقة المطلوبة لتحقيق نسبة Sharpe تساوي tSR؟

1) المدخلات
sl: عتبة وقف الخسارة
نقطة: عتبة الربح
التكرار: عدد الرهانات في السنة
tSR: متوسط ​​النسبة السنوية المستهدفة لشارب
2) الخروج
p: الحد الأدنى من الدقة p المطلوبة لتحقيق tSR
'' '
a = (freq + tSR ** 2) * (pt-sl) ** 2
b = (2 * freq * sl-tSR ** 2 * (pt-sl)) * (pt-sl)
ج = التكرار * sl ** 2
p = (- b + (b ** 2-4 * a * c) **. 5) / (2. * a)
عودة ص


تسرد القائمة 15.4 θ [p، n، π–، π +] لتردد الرهان المقدر n. في التين. يوضح 15.3 التردد المقدر اعتمادًا على p و π– ، حيث π + = 0.1 و θ * = 1.5. نظرًا لأن العتبة π– تصبح أكثر سلبية بالنسبة إلى درجة معينة p ، فإن العدد الأعلى n مطلوب لتحقيق θ * لعتبة معينة π +. نظرًا لأن درجة p تصبح أصغر لعتبة معينة π– ، يلزم وجود رقم أعلى n لتحقيق θ * لعتبة معينة π +.

ادراج 15.4. حساب وتيرة الرهان المقدر

 def binFreq(sl,pt,p,tSR): ´´´ 

نظرًا لقاعدة تداول تتميز بالمتغيرات {sl، pt، freq} ، فكم عدد الرهانات المطلوبة في السنة لتحقيق معامل Sharp tSR بدرجة من الدقة؟

ملاحظة: المعادلة مع الجذور ، تحقق من حلول غريبة.

1) المدخلات
sl: عتبة وقف الخسارة
نقطة: عتبة الربح
p: درجة الدقة p
tSR: متوسط ​​النسبة السنوية المستهدفة لشارب
2) الخروج
التكرار: عدد الرهانات اللازمة سنويا
'' '
التكرار = (tSR * (pt-sl)) ** 2 * p * (1-p) / ((pt-sl) * p + sl) ** 2 # ربما دخيلة
إن لم يكن np.isclose (binSR (sl، pt، freq، p)، tSR): return
عودة التكرار



»يمكن الاطلاع على مزيد من المعلومات حول الكتاب على موقع الناشر
» المحتويات
» مقتطفات

خصم 25 ٪ على كوبون الباعة المتجولين - التعلم الآلي

عند دفع النسخة الورقية من الكتاب ، يتم إرسال نسخة إلكترونية من الكتاب عن طريق البريد الإلكتروني.