جوليا والحوسبة المتوازية

منذ إصدارها في أغسطس 2018 ، اكتسبت Julia شعبية بنشاط من خلال إدخال أفضل 10 لغات على Github وأفضل 20 مهارات احترافية شعبية وفقًا لـ Upwork . للمبتدئين ، تبدأ الدورات وتنشر الكتب . تستخدم جوليا في تخطيط المهمة الفضائية ، والدوائية ، ونمذجة المناخ .

قبل الانتقال إلى الحوسبة الموزعة في جوليا ، دعونا ننتقل إلى تجربة أولئك الذين جربوا بالفعل هذه الفرصة ل PL جديدة للمشاكل التطبيقية - من معادلة الانتشار على اثنين من النوى ، إلى الخرائط الفلكية على الكمبيوتر العملاق.

الحوسبة المتوازية والعوامل التي تؤثر على أداء الحوسبة المتوازية

تحتوي معظم أجهزة الكمبيوتر الحديثة على أكثر من معالج واحد ، ويمكن دمج العديد من أجهزة الكمبيوتر في كتلة. يتيح لك استخدام قوة المعالجات المتعددة إجراء العديد من العمليات الحسابية بشكل أسرع. يتأثر الأداء بعاملين رئيسيين: سرعة المعالجات نفسها وسرعة الوصول إلى الذاكرة الخاصة بهم. في الكتلة ، سيكون لوحدة المعالجة المركزية هذه أسرع وصول إلى ذاكرة الوصول العشوائي الموجودة على نفس الكمبيوتر أو المضيف. والأكثر إثارة للدهشة ، أن مثل هذه المشاكل وثيقة الصلة بالكمبيوتر المحمول متعدد النواة بسبب الاختلافات في سرعة الذاكرة الرئيسية وذاكرة التخزين المؤقت. لذلك ، يجب أن تسمح لك بيئة المعالجة المتعددة الجيدة بالتحكم في استخدام جزء من الذاكرة بواسطة معالج محدد.

الحوسبة المتوازية في جوليا

جوليا لديها العديد من البدائل المضمنة للحوسبة المتوازية في كل مستوى: الموجه (SIMD) ، multithreading ، والحوسبة الموزعة.

يتيح تعدد مؤشرات جوليا الخاصة للمستخدم استخدام إمكانات الكمبيوتر المحمول متعدد النواة ، بينما تتيح لك المكالمة عن بُعد والوصول عن بُعد إمكانية توزيع العمل بين العديد من العمليات في المجموعة. بالإضافة إلى هذه العناصر الأولية المدمجة ، يوفر عدد من الحزم في نظام جوليا البيئي معالجة موازية فعالة.

ناقل الحركة التلقائي في جوليا

توفر رقائق Intel الحديثة عددًا من ملحقات مجموعة الأوامر. من بينها إصدارات مختلفة من Streaming SIMD Extension (SSE) وعدة أجيال من امتدادات المتجهات (متوفرة في أحدث مجموعات المعالجات). توفر هذه الملحقات البرمجة بأسلوب البيانات المتعددة للتعليم الفردي (SIMD) ، مما يوفر تسارعًا كبيرًا للرمز الذي يفسر مثل هذا النمط من البرمجة. يمكن لمترجم جوليا القوي في LLia إنشاء رمز آلة فعال للغاية للوظائف الأساسية والمعرفة من قبل المستخدم في أي بنية ، مثل أجهزة SIMD (المدعومة من قبل LLVM ) ، والتي تتيح للمستخدم القلق بشأن كتابة كود متخصص لكل من هذه البنيات. ميزة أخرى لاستخدام المحول البرمجي لتحسين الأداء ، بدلاً من ترميز "الحلقات الساخنة" يدويًا في التجميع ، هي أنه أفضل بكثير للمستقبل. كلما ظهرت بنية مجموعة التعليمات من الجيل التالي ، يصبح رمز جوليا المخصص تلقائيًا أسرع.

خاصية تعدد

تعدد الصفحات في جوليا عادة ما يأخذ شكل حلقات متوازية. هناك أيضًا بدائل للأقفال والذرات التي تتيح للمستخدمين مزامنة التعليمات البرمجية الخاصة بهم. بدايات جوليا المتوازية بسيطة ولكنها قوية. لقد تبين أنها تتوسع إلى آلاف العقد وتعالج تيرابايت من البيانات .

الحوسبة الموزعة

على الرغم من أن بدايات Julia المضمنة كافية للنشر المتوازي على نطاق واسع ، إلا أن هناك عددًا من الحزم لمزيد من العمل المتخصص. يوفر ClusterManagers.jl واجهات لعدد من أنظمة قائمة انتظار الوظائف التي يشيع استخدامها في مجموعات الحوسبة ، مثل Sun Grid Engine و Slurm . يوفر DistributedArrays.jl واجهة ملائمة لصفائف البيانات الموزعة عبر كتلة. يجمع هذا بين موارد ذاكرة العديد من الأجهزة ، مما يجعل من الممكن استخدام صفائف كبيرة جدًا بحيث لا يمكن وضعها على جهاز واحد. تعمل كل عملية على جزء الصفيف الذي تملكه ، وتقدم إجابة جاهزة على سؤال حول كيفية تقسيم البرنامج بين الآلات.

في بعض التطبيقات القديمة ، يفضل المستخدمون عدم إعادة التفكير في نموذجهم المتوازي ويريدون الاستمرار في استخدام التزامن MPI- style. بالنسبة لهم ، يوفر MPI.jl غلافًا رقيقًا حول MPI يتيح للمستخدمين استخدام إجراءات تمرير الرسائل على نمط MPI.

جوليا في المعركة

مشروع Celeste عبارة عن تعاون بين Julia Computing و Intel Labs و JuliaLabs @ MIT و Lawrence Berkeley National Labs وجامعة كاليفورنيا في بيركلي.

يعتبر Celeste نموذجًا هرميًا عامًا بالكامل يستخدم الاستدلال الإحصائي لتحديد موقع وخصائص مصادر الضوء في السماء حسابيًا. يسمح هذا النموذج للفلكيين بتحديد المجرات الواعدة لاستهداف المخططات الطيفية ويساعد على فهم دور الطاقة المظلمة والمادة المظلمة وهندسة الكون.

مثال من مسح سلون الرقمي للسماء (SDSS)

باستخدام قدرات الحوسبة المتوازية الخاصة بجوليا ، عالج فريق أبحاث سيليست 55 تيرابايت من البيانات المرئية وصنف 188 مليون قطعة فلكية في 15 دقيقة فقط ، مما أدى إلى أول كتالوج كامل لجميع الكائنات المرئية من Sloan Digital Sky Survey . هذه واحدة من أكبر مشاكل التحسين الرياضي التي تحلها البشرية على الإطلاق.

استخدم مشروع Celeste 9،300 عقدًا من Knights Landing (KNL) على الكمبيوتر العملاق NERSC Cori Phase II لتنفيذ 1.3 مليون مؤشر ترابط على 650،000 KNL ، مما جمع قائمة التطبيقات بسرعات تفوق بيتلافلوب واحد في الثانية ، مما جعل جوليا الديناميكية الوحيدة لغة عالية المستوى حققت مثل هذا العمل الفذ. ؟؟ لكن هل مزامنة التلسكوبات ومعالجة البيانات لصورة الثقب الأسود في 10.04.19 تحطّم هذا السجل؟ يبدو أن بيثون كان يستخدم في الغالب هناك.

البرمجة المتوازية مع جوليا باستخدام MPI

ترجمة مواد من مدونة كلاوديو فيزياء البلازما 2018-09-30

جوليا موجودة منذ عام 2012 ، وبعد أكثر من ست سنوات من التطوير ، تم إصدار الإصدار 1.0 أخيرًا. هذه مرحلة مهمة ألهمتني لإنشاء وظيفة جديدة (بعد عدة أشهر من الصمت). هذه المرة سنرى كيفية القيام بالبرمجة المتوازية في جوليا باستخدام نموذج واجهة تمرير الرسائل (MPI) من خلال مكتبة Open MPI مفتوحة المصدر. سنفعل ذلك عن طريق حل مشكلة جسدية حقيقية: انتشار الحرارة عبر منطقة ثنائية الأبعاد.

الشكل 1. حاسوب سكويا العملاق في LLNL مع ما يقرب من 1.6 مليون معالجات متاحة للمحاكاة العددية للأسلحة النووية. hpc.llnl.gov

سيكون هذا أحد تطبيقات MPI المتقدمة إلى حد ما ، ويستهدف أولئك الذين لديهم بالفعل بعض الفهم للحوسبة المتوازية. لهذا السبب ، لن أذهب خطوة بخطوة ، بل سأركز على جوانب محددة ، في رأيي ، تهم (على وجه الخصوص ، استخدام خلايا الأشباح ونقل الرسائل في شبكة ثنائية الأبعاد). وفقًا لتقليد مشاركاته الأخيرة ، سيتم وضع الرمز الذي تمت مناقشته هنا جزئيًا فقط. يرافق ذلك حل كامل الميزات يمكنك العثور عليه على Github - Diffusion.jl .

دخلت الحوسبة المتوازية "العالم التجاري" خلال السنوات القليلة الماضية. هذا حل قياسي لتطبيقات ETL (Extract-Transform-Load) ، حيث تكون المشكلة قيد النظر متوازنة بشكل محرج: يتم تنفيذ كل عملية بشكل مستقل عن جميع العمليات الأخرى ، ولا يلزم أي اتصال بالشبكة (حتى تحدث خطوة "التخفيض" النهائية ، حيث يتم تجميع كل حل محلي في الحل العالمي).

في العديد من التطبيقات العلمية ، من الضروري نقل المعلومات عبر شبكة عنقودية. غالبًا ما تكون مشكلات "الضغط الموازي" هذه محاكاة رقمية: مشكلات الفيزياء الفلكية ، نمذجة الطقس ، علم الأحياء ، الأنظمة الكمومية ، إلخ. في بعض الحالات ، يتم إجراء هذه المحاكاة على العشرات وحتى ملايين المعالجات (الشكل 1) ، ويتم توزيع الذاكرة بين المعالجات المختلفة. عادةً ما تتفاعل هذه المعالجات في كمبيوتر عملاق من خلال نموذج واجهة تمرير الرسائل (MPI).

أي شخص يعمل في الحوسبة عالية الأداء يجب أن يكون على دراية MPI. لأنها تتيح استخدام بنية الكتلة على مستوى منخفض للغاية. نظريا ، يمكن للباحث تعيين كل وحدة المعالجة المركزية الخاصة به تحميل الحوسبة الخاصة. يمكن له / لها أن يقرر بالضبط متى وما هي المعلومات التي ينبغي نقلها بين المعالجات ، وما إذا كان ينبغي أن يحدث ذلك بشكل متزامن أو غير متزامن.

والآن دعنا نعود إلى محتويات هذا المنشور ، حيث سنرى كيفية كتابة حل لمعادلة نوع الانتشار باستخدام MPI. لقد ناقشنا بالفعل مخططًا صريحًا لمعادلة أحادية البعد من هذا النوع ( بالمناسبة ، ناقشنا هذا أيضًا ). ومع ذلك ، سننظر في هذا المنشور في حل ثنائي الأبعاد.

كود جوليا المقدم هنا هو في الأساس ترجمة لرمز C / Fortran موضحة في هذا المنشور الرائع لفابيان دورناك.

في هذا المنشور ، لن أحلل بالتفصيل سرعة القياس وعدد المعالجات. يرجع السبب الرئيسي في ذلك إلى امتلاك معالجين فقط يمكنني تشغيلهما في المنزل (معالج Intel Core i7 على جهاز MacBook Pro) ... ومع ذلك ، لا يزال بإمكاني القول بفخر أن رمز جوليا المقدم في هذا المنشور ، يظهر تسارع كبير عند استخدام اثنين من المعالجات ضد واحد. على أي حال: إنه أسرع من رموز Fortran و C المكافئة! (المزيد حول هذا لاحقًا)

فيما يلي المواضيع التي سنغطيها في هذا المنشور:

• جوليا: انطباعاتي الأولى
• كيفية تثبيت فتح MPI على جهاز الكمبيوتر الخاص بك
• المشكلة: الانتشار من خلال مجال ثنائي الأبعاد
• التواصل بين المعالج: الحاجة إلى خلايا الأشباح
• باستخدام MPI
• التصور الحل
• إنتاجية
• النتائج

1. الانطباعات الأولى لجوليا

في الواقع ، قابلت جوليا مؤخرًا ، لذا قررت التركيز على "الانطباعات الأولى" هنا.

السبب الرئيسي الذي جعلني مهتمًا بجوليا هو أنها تعد بأن تكون إطارًا للأغراض العامة مع أداء مشابه لأداء C و Fortran ، مع الحفاظ على المرونة وسهولة استخدام لغات البرمجة النصية مثل Matlab أو Python . في الواقع ، يجب أن تكون Julia قادرة على كتابة تطبيقات Data Science / High-Performance-Computing التي تعمل على الكمبيوتر المحلي أو في السحابة أو على أجهزة الكمبيوتر العملاقة للشركات.

أحد الجوانب التي لا أحبها هو سير العمل ، والذي يبدو أنه دون المستوى الأمثل لأولئك الذين يستخدمون IntelliJ و PyCharm يوميًا مثلي (البرنامج المساعد IntelliJ Julia سيء جدًا ). جربت أيضًا جهاز Juno IDE ، والذي ربما يكون أفضل حل في الوقت الحالي ، لكن ما زلت بحاجة إلى التعود عليه.

أحد الجوانب التي توضح كيف أن جوليا لم تصل بعد إلى "نضجها" هو مدى تعدد وتوثيق وثائق العديد من الحزم ( بالنسبة للحزم التي تم الحفاظ عليها واقفة على قدميها ، تم تجريف كل شيء منذ العام الماضي ). ما زلت لم أجد طريقة لكتابة مصفوفة من أرقام الفاصلة العائمة على القرص في شكل منسق ( أصبح من السهل الآن العثور عليه ). بالطبع ، يمكنك الكتابة إلى القرص لكل عنصر من عناصر المصفوفة في حلقة مزدوجة مقابل ، ولكن يجب توفير حلول أفضل. إنه من الصعب العثور على هذه المعلومات ، ويجب أن تكون الوثائق شاملة.

هناك جانب آخر يبرز عند استخدام جوليا لأول مرة وهو اختيار استخدام الفهرسة من أحدها للصفائف. على الرغم من أنني أجد هذا مزعجًا بعض الشيء من الناحية العملية ، إلا أنه بالتأكيد لا يخرق الاتفاقية ، نظرًا لأنه ليس فريدًا بالنسبة لجوليا (يستخدم Matlab و Fortran أيضًا الفهرسة بدءًا من واحد).

الآن ، إلى الجانب الجيد والأكثر أهمية: يمكن أن تكون جوليا سريعة جدًا حقًا. لقد تأثرت برؤية كيف يمكن لشفرة جوليا التي كتبتها لهذا المنشور أن تعمل بشكل أفضل من شفرة فورتران وجيم المكافئة ، على الرغم من أنني قمت في الأساس بترجمتها إلى جوليا. ألق نظرة على قسم الأداء إذا كنت مهتمًا.

2. تثبيت فتح MPI

Open MPI هي مكتبة واجهة مفتوحة المصدر. وتشمل المكتبات المعروفة الأخرى MPICH و MVAPICH. تعد MVAPICH ، التي طورتها جامعة ولاية أوهايو ، المكتبة الأكثر تقدماً حاليًا لأنها يمكنها أيضًا دعم مجموعات GPU - وهي مفيدة بشكل خاص لتطبيقات التعليم العميق (يوجد تعاون وثيق بين NVIDIA وفريق MVAPICH).

كل هذه المكتبات مبنية على واجهة مشتركة: واجهة برمجة تطبيقات MPI. لذلك ، لا يهم إذا كنت تستخدم مكتبة أو مكتبة أخرى: قد تظل الشفرة التي كتبتها كما هي.

مشروع MPI.jl على جيثب هو غلاف ل MPI. تحت الغطاء ، فإنه يستخدم منشآت C و Fortran MPI. إنه يعمل بشكل رائع ، على الرغم من أنه يفتقر إلى بعض الميزات المتوفرة في هذه اللغات الأخرى.

لتشغيل MPI على Julia ، ستحتاج إلى تثبيت Open MPI بشكل منفصل على جهاز الكمبيوتر الخاص بك. إذا كان لديك جهاز Mac ، فقد وجدت هذا الدليل مفيدًا للغاية. من المهم ملاحظة أنك ستحتاج أيضًا إلى تثبيت gcc (مترجم GNU) لأن Open MPI يتطلب المترجمين Fortran و C. لقد قمت بتثبيت إصدار Open MPI 3.1.1 ، والذي تم تأكيده أيضًا بواسطة mpiexec --version على جهاز طرفيه.

بعد تثبيت Open MPI على جهاز الكمبيوتر الخاص بك ، يجب عليك تثبيت cmake . مرة أخرى ، إذا كان لديك جهاز Mac ، فسيكون الأمر سهلاً كما هو الحال في الكتابة إلى brew install cmake على الجهاز الطرفي.

في الوقت الحالي ، أنت جاهز لتثبيت حزمة MPI في جوليا. افتح Julia REPL واكتب using Pkg Pkg.add («MPI») . عادةً في هذه المرحلة ، يجب أن تكون قادرًا على استيراد الحزمة باستخدام MPI للاستيراد. ومع ذلك ، كان علي أيضًا إنشاء الحزمة من خلال Pkg.build («MPI») قبل أن تعمل.

3. المشكلة: معادلة الانتشار ثنائية الأبعاد

معادلة الانتشار هي مثال لمعادلة تفاضلية جزئية مكافئية. يصف بعض الظواهر مثل انتشار الحرارة أو تركيز التركيز (قانون فيك الثاني). في بعدين مكانيين ، تتم كتابة معادلة الانتشار

قرار $$$u (x، y، t)$ يوضح كيف تتغير درجة الحرارة / التركيز (اعتمادًا على ما إذا كنا ندرس توزيع الحرارة أو انتشار المواد) في المكان والزمان. في الواقع ، تمثل المتغيرات x و y الإحداثيات المكانية ، ويتم تمثيل مكون الوقت بواسطة المتغير t . الكمية D هي "معامل الانتشار" وتحدد مدى سرعة انتشار الحرارة ، على سبيل المثال ، عبر المنطقة المادية. على غرار ما تمت مناقشته (بمزيد من التفاصيل) في منشور المدونة السابق ، يمكن تقدير المعادلة المذكورة أعلاه باستخدام ما يسمى "المخطط الصريح" للحل. لن أخوض في التفاصيل التي يمكنك العثور عليها على المدونة ، فقط اكتب حلًا رقميًا في النموذج التالي:

حيث i و k مؤشران يعملان على طول الشبكة المكانية ، j في الوقت المناسب. يتم تعبئة الطبقة الزمنية الأولى من الشروط الأولية ، ولكل طبقة لاحقة $$$u ^ {j + 1} _ {i، k}$ تحسب باستخدام قيم الطبقة السابقة. في الشكل ، تشير العقد الحمراء إلى عقد الطبقة $$$u ^ {j}$ وهي ضرورية لحساب القيمة في هذه النقطة $$$u ^ {j + 1} _ {i، k}$

المعادلة (1) هي في الحقيقة كل ما هو مطلوب من أجل إيجاد حل على المنطقة بأكملها في كل خطوة زمنية لاحقة. من السهل جدًا تنفيذ التعليمات البرمجية التي تقوم بذلك بالتتابع مع عملية واحدة على وحدة المعالجة المركزية. ومع ذلك ، نريد هنا مناقشة تطبيق مواز يستخدم عدة عمليات.

ستكون كل عملية مسؤولة عن إيجاد حل في جزء من المجال المكاني بأكمله. تتطلب مشكلات مثل نشر الحرارة ، والتي ليست مرشحة واضحة للحوسبة الموزعة ، تبادل المعلومات بين العمليات. لتوضيح هذه النقطة ، دعونا ننظر إلى الصورة

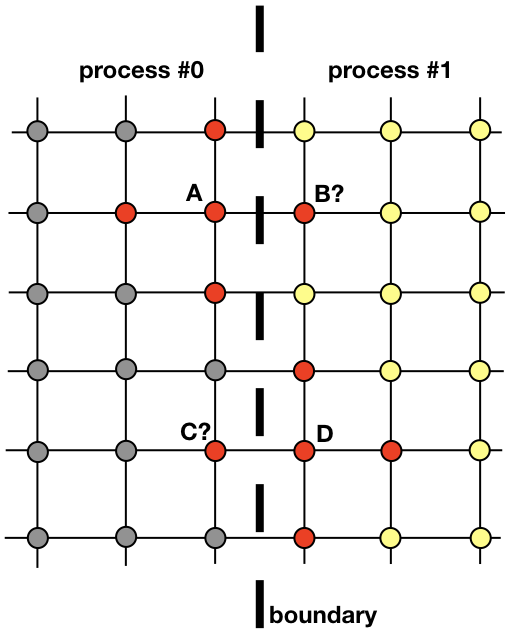
يجب أن تتفاعل عمليتان متجاورتان لإيجاد حل بالقرب من الحدود. يجب أن تعرف العملية 0 قيمة الحل في B من أجل حساب الحل عند نقطة الشبكة A. وبالمثل ، يجب أن تعرف العملية 1 القيمة عند النقطة C من أجل حساب الحل عند نقطة الشبكة D. هذه القيم غير معروفة للعمليات حتى يكون هناك اتصال بين العمليات 0 و 1 .

يوضح كيف ستحتاج العمليات 0 و 1 إلى التفاعل من أجل تقييم حل بالقرب من الحدود. هذا هو المكان الذي يدخل MPI المشهد. في القسم التالي ، سننظر في طريقة فعالة للرسائل.

4. التواصل بين العمليات: خلايا الأشباح

مفهوم مهم في ديناميات الموائع الحسابية هو مفهوم خلايا الأشباح. يكون هذا المفهوم مفيدًا عندما يتم تقسيم المجال المكاني إلى عدة نطاقات فرعية ، يتم حل كل منها من خلال عملية واحدة.

لفهم ما هي خلايا الأشباح ، دعونا ننظر إلى منطقتين متجاورتين في الصورة السابقة مرة أخرى. العملية 0 هي المسؤولة عن إيجاد الحل على الجانب الأيسر ، في حين أن العملية 1 تجدها على الجانب الأيمن من المجال المكاني. ومع ذلك ، نظرًا لشكل الاستنسل (الشكل 2) بالقرب من الحدود ، سيتعين على كلتا العمليتين تبادل البيانات مع بعضها البعض. هذه هي المشكلة: من غير الفعّال أن تتواصل العملية 0 والعملية 1 في كل مرة يحتاجون فيها إلى عقدة من عملية مجاورة: سيؤدي ذلك إلى تكاليف اتصال غير مقبولة.

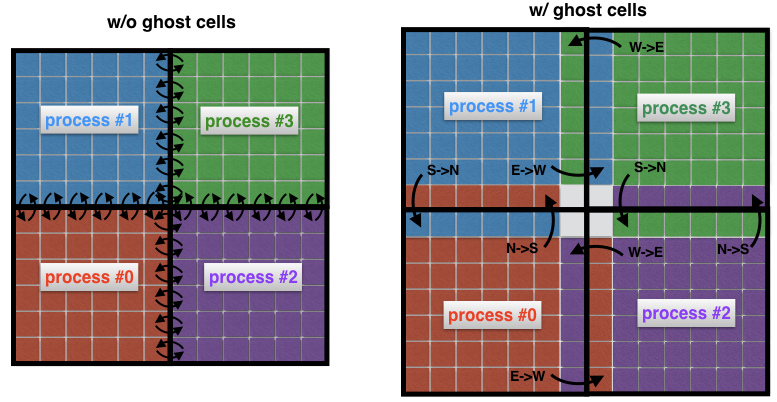
الشكل 4: الاتصال بين العمليات التي لا تحتوي على خلايا خفية (يسار). بدون خلايا وسيطة ، يجب على كل خلية على حدود المجال الفرعي إرسال رسالتها الخاصة إلى عملية مجاورة. يتيح لك استخدام الخلايا الخفية تقليل عدد الرسائل المرسلة ، حيث إن العديد من الخلايا التي تنتمي إلى حدود العملية تتبادل رسالة واحدة في كل مرة. هنا ، على سبيل المثال ، تنقل العملية 0 الحدود الشمالية بأكملها إلى العملية 1 ، والحد الشرقي بأكمله يعالج العملية 2.

بدلاً من ذلك ، من الممارسات الشائعة إحاطة النطاقات الفرعية "الحقيقية" بخلايا إضافية تسمى خلايا الأشباح ، كما هو موضح في الشكل 4 (يمين). هذه الخلايا الشبح هي نسخ من الحل على حدود المجالات الفرعية المجاورة. في كل خطوة زمنية ، يتم تمرير الحدود القديمة لكل مجال فرعي إلى الجيران. يتيح لك ذلك حساب حل جديد على حدود نطاق فرعي مع انخفاض الاتصالات بشكل ملحوظ. التأثير الصافي هو تسريع الرمز.

5. باستخدام MPI

هناك العديد من البرامج التعليمية MPI. هنا أريد فقط أن أصف الأوامر المعبر عنها بلغة MPI.jl shell لجوليا والتي اعتدت على حلها مشكلة الانتشار ثنائي الأبعاد. هذه هي بعض الأوامر الأساسية التي يتم استخدامها في كل تطبيق MPI تقريبًا.

5.1 إيجاد جيران العملية

من أجل مهمتنا ، سنحلل منطقتنا ثنائية الأبعاد إلى العديد من النطاقات الفرعية المستطيلة ، كما هو مبين في الشكل أدناه.

الشكل 5 الشكل 5. التحلل الديكارتي لمنطقة ثنائية الأبعاد مقسمة إلى 12 مجالا فرعيا. لاحظ أن صفوف MPI (معرفات العملية) تبدأ من الصفر.

لاحظ أنه يتم عكس محوري x و y بالنسبة للاستخدام العادي لربط محور x مع الصفوف ومحور y مع أعمدة مصفوفة الحل.

للتواصل بين العمليات المختلفة ، يجب أن تعرف كل عملية جيرانها. يوجد أمر MPI مفيد جدًا يقوم بذلك تلقائيًا ويسمى MPI_Cart_create . لسوء الحظ ، لا تتضمن shell Julia MPI هذا الأمر المتقدم (وإضافته لا يبدو تافهاً) ، لذلك قررت بدلاً من ذلك إنشاء وظيفة تؤدي نفس المهمة. لجعله أكثر إحكاما ، كنت في كثير من الأحيان تستخدم المشغل الثلاثي . يمكنك العثور على هذه الوظيفة أدناه.

 function neighbors(my_id::Int, nproc::Int, nx_domains::Int, ny_domains::Int) id_pos = Array{Int,2}(undef, nx_domains, ny_domains) for id = 0:nproc-1 n_row = (id+1) % nx_domains > 0 ? (id+1) % nx_domains : nx_domains n_col = ceil(Int, (id + 1) / nx_domains) if (id == my_id) global my_row = n_row global my_col = n_col end id_pos[n_row, n_col] = id end neighbor_N = my_row + 1 <= nx_domains ? my_row + 1 : -1 neighbor_S = my_row - 1 > 0 ? my_row - 1 : -1 neighbor_E = my_col + 1 <= ny_domains ? my_col + 1 : -1 neighbor_W = my_col - 1 > 0 ? my_col - 1 : -1 neighbors = Dict{String,Int}() neighbors["N"] = neighbor_N >= 0 ? id_pos[neighbor_N, my_col] : -1 neighbors["S"] = neighbor_S >= 0 ? id_pos[neighbor_S, my_col] : -1 neighbors["E"] = neighbor_E >= 0 ? id_pos[my_row, neighbor_E] : -1 neighbors["W"] = neighbor_W >= 0 ? id_pos[my_row, neighbor_W] : -1 return neighbors end 

فعلنا نفس الشيء عندما بنينا متاهات

المدخلات إلى هذه الوظيفة هي my_id ، وهي رتبة (أو معرّف) العملية ، وعدد العمليات nproc ، وعدد الأقسام في الاتجاه x nx_domains وعدد الأقسام في الاتجاه y ny_domains .

دعونا التحقق من هذه الميزة الآن. على سبيل المثال ، مرة أخرى تبحث في التين. 5 ، يمكننا التحقق من الإخراج لعملية المرتبة 4 وعملية المرتبة 11. دعنا نقود إلى REPL:

 julia> neighbors(4, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 3 "W" => 1 "N" => 5 "E" => 7 

و

 julia> neighbors(11, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 10 "W" => 8 "N" => -1 "E" => -1 

كما ترون ، أنا استخدم الاتجاهات الأساسية "N" و "S" و "E" و "W" للإشارة إلى موقع الجار. على سبيل المثال ، تحتوي العملية 4 على العملية 3 كجارة تقع جنوب موقعها. يمكنك التحقق من صحة جميع النتائج المذكورة أعلاه ، بالنظر إلى أن "-1" في المثال الثاني يعني أنه لم يتم العثور على جيران على الجانبين "الشمالي" و "الشرقي" للعملية 11.

5.2 المراسلة

كما رأينا سابقًا ، في كل تكرار ، ترسل كل عملية حدودها إلى العمليات المجاورة. في نفس الوقت ، تتلقى كل عملية بيانات من جيرانها. يتم تخزين هذه البيانات من قبل كل عملية في شكل "خلايا خفية" وتستخدم لحساب الحل بالقرب من حدود كل مجال فرعي.

يحتوي MPI على أمر MPI_Sendrecv مفيد جدًا يتيح لك إرسال واستقبال الرسائل في وقت واحد بين عمليتين. لسوء الحظ ، لا توفر MPI.jl هذه الوظيفة ، ومع ذلك لا يزال من الممكن تحقيق نفس النتيجة باستخدام MPI_Send و MPI_Receive منفصل.

إليك ما تم القيام به في وظيفة updateBound! التالية updateBound! الذي يقوم بتحديث الخلايا الشبح في كل تكرار. المدخلات إلى هذه الوظيفة هي حل عالمي ثنائي الأبعاد u ، يتضمن خلايا خفية ، وكذلك جميع المعلومات المتعلقة بعملية محددة تؤدي وظيفة (ما هي رتبتها ، وما هي إحداثيات مجالها الفرعي ، وما هي جيرانها). تقوم الوظيفة أولاً بإرسال حدودها إلى الجيران ، ثم تستقبل حدودها. يتم الانتهاء من الجزء MPI.Waitall! من خلال فريق MPI.Waitall! ، مما يضمن استلام جميع الرسائل المتوقعة قبل تحديث الخلايا الجانبية لنطاق فرعي معين.

 function updateBound!(u::Array{Float64,2}, size_total_x, size_total_y, neighbors, comm, me, xs, ys, xe, ye, xcell, ycell, nproc) mep1 = me + 1 #assume, to start with, that this process is not going to receive anything rreq = Dict{String, MPI.Request}( "N" => MPI.REQUEST_NULL, "S" => MPI.REQUEST_NULL, "E" => MPI.REQUEST_NULL, "W" => MPI.REQUEST_NULL ) recv = Dict{String, Array{Float64,1}}() ghost_boundaries = Dict{String, Any}( "N" => (xe[mep1]+1, ys[mep1]:ye[mep1]), "S" => (xs[mep1]-1, ys[mep1]:ye[mep1]), "E" => (xs[mep1]:xe[mep1], ye[mep1]+1), "W" => (xs[mep1]:xe[mep1], ys[mep1]-1) ) is_receiving = Dict{String, Bool}("N" => false, "S" => false, "E" => false, "W" => false) #send neighbors["N"] >=0 && MPI.Isend(u[xe[mep1], ys[mep1]:ye[mep1]], neighbors["N"], me + 40, comm) neighbors["S"] >=0 && MPI.Isend(u[xs[mep1], ys[mep1]:ye[mep1]], neighbors["S"], me + 50, comm) neighbors["E"] >=0 && MPI.Isend(u[xs[mep1]:xe[mep1], ye[mep1]], neighbors["E"], me + 60, comm) neighbors["W"] >=0 && MPI.Isend(u[xs[mep1]:xe[mep1], ys[mep1]], neighbors["W"], me + 70, comm) #receive if (neighbors["N"] >= 0) recv["N"] = Array{Float64,1}(undef, ycell) is_receiving["N"] = true rreq["N"] = MPI.Irecv!(recv["N"], neighbors["N"], neighbors["N"] + 50, comm) end if (neighbors["S"] >= 0) recv["S"] = Array{Float64,1}(undef, ycell) is_receiving["S"] = true rreq["S"] = MPI.Irecv!(recv["S"], neighbors["S"], neighbors["S"] + 40, comm) end if (neighbors["E"] >= 0) recv["E"] = Array{Float64,1}(undef, xcell) is_receiving["E"] = true rreq["E"] = MPI.Irecv!(recv["E"], neighbors["E"], neighbors["E"] + 70, comm) end if (neighbors["W"] >= 0) recv["W"] = Array{Float64,1}(undef, xcell) is_receiving["W"] = true rreq["W"] = MPI.Irecv!(recv["W"], neighbors["W"], neighbors["W"] + 60, comm) end MPI.Waitall!([rreq[k] for k in keys(rreq)]) for (k, v) in is_receiving if v u[ghost_boundaries[k][1], ghost_boundaries[k][2]] = recv[k] end end end 

5. التصور الحل

تتم تهيئة المجال بقيمة ثابتة u = +10 حول الحدود ، والتي يمكن تفسيرها على أنها وجود مصدر ثابت لدرجة الحرارة على الحدود. الشرط الأولي u = −10 داخل المنطقة (الشكل 6 على اليسار). بمرور الوقت ، تنتشر القيمة u = 10 عند الحدود إلى وسط المنطقة. على سبيل المثال ، في الخطوة j = 15203 يبدو الحل كما هو موضح في الشكل. 6 على اليمين.

مع زيادة الوقت t ، يصبح الحل أكثر تجانسًا ، من الناحية النظرية $$$t \ rightarrow + \ infty$ لن تصبح u = +10 جميع أنحاء المجال.

التين. 6. الشرط الأولي (يسار) والحل في الخطوة 15203 في الوقت المناسب (يمين). يتم تخزين حدود المنطقة دائمًا في u = +10. بمرور الوقت ، يصبح الحل أكثر اتساقًا ويميل إلى أن يكون أقرب وأقرب إلى القيمة u = +10 في جميع أنحاء المنطقة.

6. الأداء

لقد تأثرت بشدة عندما اختبرت أداء تطبيق Julia مقارنةً بـ Fortran و C: لقد وجدت أن تطبيق Julia هو الأسرع!

قبل الخوض في المقارنة ، دعونا نلقي نظرة على أداء MPI لرمز جوليا نفسه. يوضح الشكل 7 نسبة وقت التشغيل عند العمل مع العمليات من 1 إلى 2 (وحدة المعالجة المركزية). من الناحية المثالية ، ترغب في أن يكون هذا الرقم قريبًا من 2 ، أي يجب أن يكون العمل مع اثنين من المعالجات أسرع من معالج واحد. بدلاً من ذلك ، لوحظ أنه بالنسبة لأحجام المهام الصغيرة (شبكة تتكون من 128 × 128 خلية) ، يكون لوقت التجميع وحمول الاتصال تأثير سلبي على إجمالي وقت التنفيذ: التسارع أقل من واحد. تصبح ميزة استخدام عمليات متعددة واضحة فقط للمهام الأكبر حجمًا.

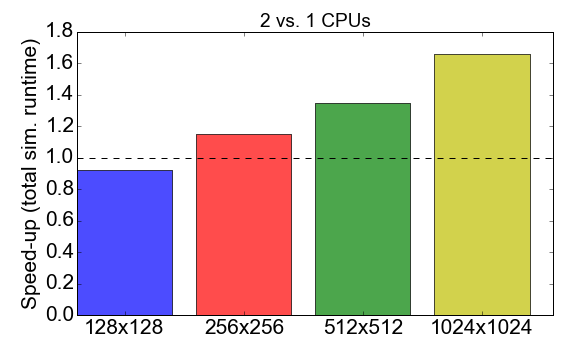
الشكل 7. تسريع تنفيذ جوليا MPI مع عمليتين مقابل عملية واحدة ، وهذا يتوقف على تعقيد المهمة (حجم الشبكة). يشير "التسريع" إلى نسبة إجمالي وقت التنفيذ باستخدام عملية واحدة إلى عمليتين.

والآن منعطفا غير متوقع: في التين. يوضح الشكل 8 أن تطبيق Julia أسرع من Fortran و C للمهام ذات الحجم 256 × 256 و 512 × 512 (فقط تلك التي اختبرتها). هنا أقيس فقط الوقت اللازم لإكمال حلقة التكرار الرئيسية. أعتقد أن هذه مقارنة عادلة ، لأن عمليات المحاكاة المطولة ستكون أكبر مساهمة في إجمالي وقت التشغيل.

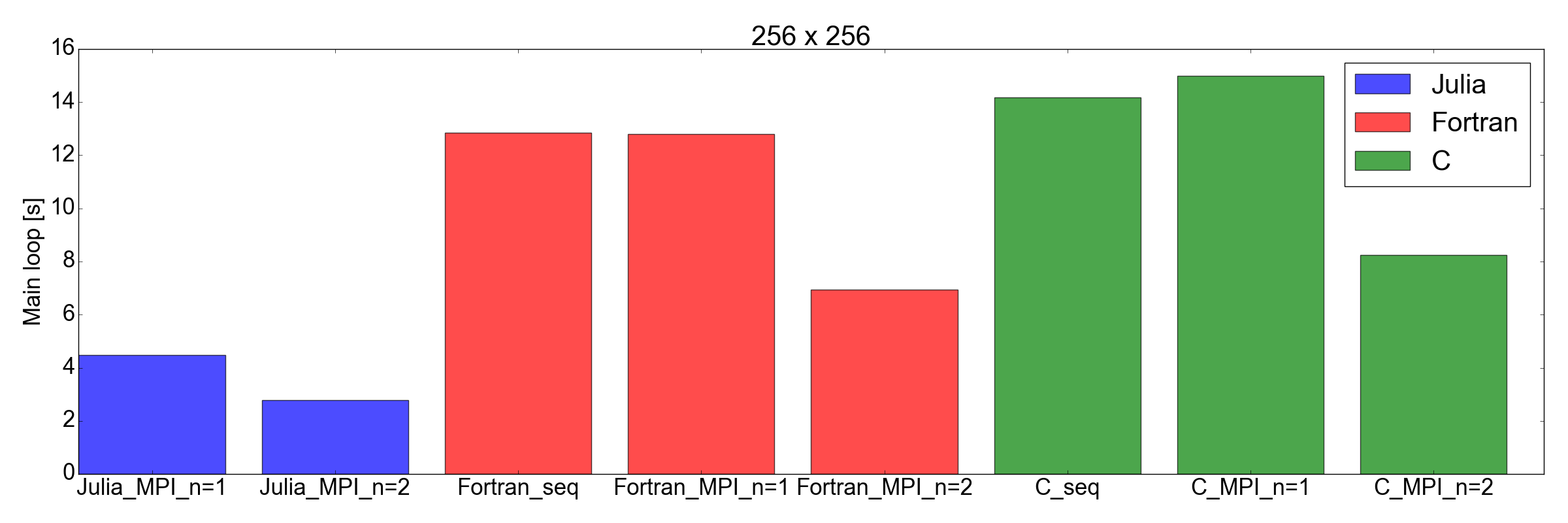
الشكل 8. أداء جوليا مقابل فورتران مقابل جيم لأحجام شبكتين: 256 × 256 (أعلى) و 512 × 512 (أسفل). هذا يدل على أن جوليا هي أفضل اللغات أداء. يتم قياس الأداء على أنه الوقت الذي يستغرقه تنفيذ عدد محدد من التكرارات في حلقة الرمز الرئيسي.

النتائج

قبل بدء هذا المنشور ، كنت متشككًا في أن جوليا يمكنها التنافس مع سرعة Fortran و C في التطبيقات العلمية. السبب الرئيسي هو أنني كنت قد قمت سابقًا بترجمة الكود الأكاديمي الذي يحتوي على حوالي 2000 سطر من فورتران إلى جوليا 0.6 ، وقد لاحظت انخفاضًا في الأداء حوالي 3 مرات.

لكن هذه المرة ... أنا معجب جدا. لقد قمت بالفعل بترجمة تطبيق MPI الحالي المكتوب في Fortran و C إلى Julia 1.0. النتائج المبينة في التين. 8 ، تحدث عن نفسها: جوليا يبدو أنها الأسرع حتى الآن. يرجى ملاحظة أنني لم تأخذ في الاعتبار وقت التجميع الطويل الذي يستغرقه برنامج التحويل البرمجي Julia ، حيث سيكون هذا عاملًا مهمًا للتطبيقات "الحقيقية" التي تتطلب ساعات لإكمالها.

يجب أن أضيف أيضًا أن اختباراتي ليست ، بالطبع ، شاملة كما يجب أن تكون للمقارنة الدقيقة. في الحقيقة ، سأشعر بالفضول لمعرفة كيفية عمل الكود مع أكثر من معالجين (أنا مقيد بجهاز الكمبيوتر المحمول الشخصي في منزلي) ومع أجهزة أخرى (انظر Diffusion.jl ).

على أي حال ، أقنعني هذا التمرين أن الأمر يستحق قضاء المزيد من الوقت في دراسة واستخدام جوليا لعلوم البيانات والتطبيقات العلمية. الذهاب إلى إنجازات جديدة!

مراجع

• الإصدار MPI du code de résolution numérique de l'équation de chaleur 2D
• الحوسبة المتوازية
• البرمجة المتوازية مع جوليا باستخدام MPI
• برنامج سيليست