أشجار البحث الثنائية المتوازنة: التنفيذ على جوليا

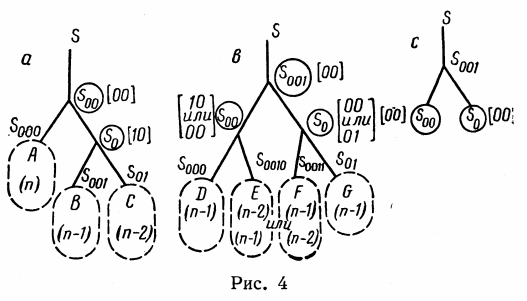
رسم توضيحي من أعمال G.M. أديلسون ولسكي وإي إم لانديس 1962

أشجار البحث هي هياكل بيانات للتخزين المنظم والبحث البسيط للعناصر. تُستخدم أشجار البحث الثنائية على نطاق واسع ، حيث يكون لكل عقدة طفلان فقط. في هذه المقالة ، نعتبر طريقتين لتنظيم أشجار البحث الثنائية: خوارزميات Adelson-Welsky و Landis (أشجار AVL) وأشجار AVL الضعيفة (أشجار WAVL).

لنبدأ بالتعاريف. تتكون الشجرة الثنائية من العقد ، تخزن كل عقدة سجلًا في شكل أزواج ذات قيمة مفتاح (أو ، في الحالة البسيطة ، قيم فقط) وليس لها أكثر من طفلين . تتميز العقد المنحدرة من اليمين واليسار ، ويتم استيفاء شرط ترتيب المفاتيح: لم يعد مفتاح الطفل الأيسر ، ولا يقل المفتاح الأيمن عن مفتاح العقدة الأصل. بالإضافة إلى ذلك ، يمكن تخزين معلومات الخدمة (وعادةً ما يتم تخزينها) في العقد - على سبيل المثال ، رابط للعقدة الأصل أو بيانات أخرى. الحالات الخاصة هي العقدة الجذرية التي تدخل منها الشجرة ، والعقدة الفارغة التي لا تخزن أي معلومات. تسمى العقد التي يكون فيها كلا من أحفادها أوراق شجرة. العقدة مع جميع أحفاد يشكل شجرة فرعية . وبالتالي ، كل عقدة هي إما جذر الشجرة الفرعية أو ورقة.

يسمح لك هذا التعريف ببناء بنية بسيطة لتخزين العقد والشجرة نفسها. نحن نفترض أن العقدة الفارغة لها قيمة خاصة nothing النوع Nothing . ثم في العقدة يكفي لتخزين المراجع إلى ذرية اليمين واليسار وإلى الوالد. تحتوي بنية تخزين الشجرة على رابط لعقدة الجذر فقط.

 # K -   # V -    mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} end mutable struct BST{K, V} root::BSTNode{K,V} end 

في هذه الحالة ، يطرح السؤال حول كيفية تمثيل شجرة فارغة. للقيام بذلك ، نستخدم النهج المتبع في كتاب "الخوارزميات: البناء والتحليل" وإدراج كنقطة دخول إلى الشجرة ليس جذرًا ، ولكن عقدة وهمية ، والتي ستكون أصلها الخاص. لإنشاء مثل هذه العقدة ، قم بإضافة المنشئات إلى وصف بنية BSTNode:

 mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} #   function BSTNode{K,V}() where {K,V} node = new{K,V}() node.parent = node node.left = node.right = nothing return node end #    - function BSTNode{K,V}(key, value) where {K, V} node = new{K,V}() node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end BSTNode() = BSTNode{Any, Any}() #     ! struct BST{K, V} entry::BSTNode{K,V} BST{K,V}() where {K,V} = new{K,V}(BSTNode{K,V}()) end BST() = BST{Any, Any}() Base.isempty(bst::BST) = bst.entry.left == nothing 

في هذه الحالة ، يمكن إجراء بنية BST دون تغيير ، لأن لن تحتاج بعد ذلك إلى تغيير رابط نقطة الدخول. علاوة على ذلك ، نفترض أن العقدة الجذرية للشجرة هي على الفور المنحدر الأيمن والأيسر لعقدة الإدخال.

العملية الرئيسية التي تحتاج إليها أشجار البحث هي ، بطبيعة الحال ، البحث عن العناصر. نظرًا لأن مفتاح الطفل الأيسر لم يعد ، والمفتاح الأيمن ليس أقل من المفتاح الأصل ، تتم كتابة إجراء البحث عن العنصر ببساطة شديدة: بدءًا من جذر الشجرة ، قارن مفتاح الإدخال بمفتاح العقدة الحالية ؛ إذا كانت المفاتيح متطابقة ، فإننا نرجع القيمة ؛ وإلا ، انتقل إلى الشجرة الفرعية اليسرى أو اليمنى ، وفقًا لترتيب المفاتيح. إذا وصلوا في الوقت نفسه إلى عقدة فارغة - لا يوجد مفتاح في الشجرة ، قم برمي استثناء.

 #   Base.getindex()    #      tree[key] function Base.getindex(bst::BST{K,V}, key) where {K,V} key = convert(K, key) node = bst.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

من الواضح أن البحث عن عنصر بالمفتاح يستغرق O ( h ) وقتًا ، حيث h هو ارتفاع الشجرة ، أي أقصى مسافة من الجذر إلى ورقة. من السهل حساب أن الشجرة الثنائية ذات الارتفاع h يمكن أن تحتوي على أكثر من ^{ساعتين + 1} -1 إذا كانت مكتظة بالسكان ، أي جميع العقد ، باستثناء ، ربما ، الطبقة المتطرفة للغاية ، لديها كلا من أحفاد. بالإضافة إلى ذلك ، من الواضح أن أي تسلسل معين من المفاتيح مقدمًا يمكن أن يؤدي إلى مثل هذه الشجرة الكثيفة. هذا يعطي سلوكًا مقاربًا متفائلًا للغاية للبحث عن عنصر في شجرة مع بنائه الأمثل في الوقت O (log ₂ N ) ، حيث N هو عدد العناصر.

بطبيعة الحال ، يجب إنشاء الخوارزمية لإضافة عنصر إلى شجرة البحث بطريقة تتحقق الشرط حسب ترتيب المفاتيح. لنكتب تنفيذًا ساذجًا لإدراج عنصر حسب المفتاح:

 #   Base.setindex!()    #       tree[key] = value function Base.setindex!(bst::BST{K,V}, val::SV, key::SK) where {K, V} key, value = convert(K, key), convert(V, val) parent = bst.entry.left #   -     if parent == nothing newnode.parent = bst.entry bst.entry.left = bst.entry.right = newnode return val end key_found = false while !key_found if key < parent.key if parent.left == nothing parent.left = BSTNode{K,V}(key, value) parent.left.parent = parent key_found = true else parent = parent.left end elseif key > parent.key if parent.right == nothing parent.right = BSTNode{K,V}(key, value) newnode.parent = parent key_found = true else parent = parent.right end else key_found = true parent.value = value end end return val end 

لسوء الحظ ، فإن البناء الساذج للشجرة سوف يعطي البنية المطلوبة فقط على بيانات الإدخال العشوائية ، ولكن في الواقع غالباً ما تكون منظمة. في أسوأ الحالات ، إذا كانت المفاتيح الواردة مرتبة ترتيبًا صارمًا (على الأقل بترتيب تصاعدي ، على الأقل بترتيب تنازلي) ، فإن إنشاء الشجرة الساذجة سيرسل عناصر جديدة طوال الوقت في اتجاه واحد ، يجمع في الواقع قائمة خطية. من السهل تخمين أن إدخال العناصر ، أن البحث سوف يحدث مع مثل هذا الهيكل خلال O ( N ) ، والذي ينفي كل الجهود المبذولة لبناء بنية بيانات معقدة.

الخلاصة: يجب أن تكون شجرة البحث متوازنة أثناء البناء ، أي قم بمحاذاة ارتفاع الشجرة الفرعية اليمنى واليسرى في كل عقدة. هناك عدة طرق لتحقيق التوازن. أبسطها هو تحديد عدد معين من عمليات الإدراج أو الحذف ، وبعد ذلك سيتم إعادة توازن الشجرة. في هذه الحالة ، ستكون الشجرة في حالة "قيد التشغيل" إلى حد ما قبل الموازنة ، ولهذا السبب سيستغرق التوازن حوالي O ( N ) من الوقت في أسوأ الحالات ، ولكن سيتم تنفيذ العمليات اللاحقة حتى حد معين للإدخال / الحذف في وقت لوغاريتمي. خيار آخر هو إنشاء خوارزميات الإدراج والحذف على الفور بحيث تظل الشجرة متوازنة دائمًا ، مما يعطي التعقيد الزمني المضمون O (السجل ₂ N ) لأي عملية.

نظرًا لوجود خوارزميات يُسمح فيها للشجرة "بالانتشار" ، ولكن بعد ذلك ، يمكن تنفيذ العمليات لفترة طويلة إلى حد ما في وقت لوغاريتمي ، قبل أن تتم إعادة الشجرة إلى حالة متوازنة لفترة طويلة ، يتم تمييز وقت الإدراج / الحذف المضمون والمستهلك . بالنسبة إلى بعض عمليات تنفيذ العمليات التي تتضمن أشجار البحث الثنائية ، يتم ضمان تعقيد إدخال وحذف O (log ₂ N ) ، ويتم إطفاءه بالنسبة للبعض ، مع تدهور إلى O ( N ).

Adelson-Welsky و Landis Algorithm (AVL)

تم اقتراح التنفيذ الأول لشجرة البحث الثنائية ذاتي التوازن في عام 1962 بواسطة Adelson-Welsky و Landis. في الأدب الحديث على الحروف الأولى من الألقاب يسمى هذا الهيكل أشجار AVL . يوصف الهيكل بالخصائص التالية:

1. الترتيب: بالنسبة لأي عقدة ، يكون المفتاح في أعلى الشجرة اليسرى أقل من المفتاح في أعلى الشجرة الفرعية اليمنى (إذا لم تكن أحفاد العقد فارغة).
2. زيادة الارتفاع: ارتفاع العقدة الأصل هو واحد أكثر من الحد الأقصى لارتفاع أحفادها. يمكن اعتبار ارتفاع العقد الفارغة مساوياً للصفر.
3. توازن AVL: بالنسبة لأي عقدة ، تختلف ارتفاعات الشجرة الفرعية اليمنى واليسرى بما لا يزيد عن 1.

من هذه الخصائص ، يكون ارتفاع الشجرة بأكملها هو O (log ₂ N ) ، حيث N هو عدد السجلات المخزنة في الشجرة ، مما يعني أنه يتم البحث عن السجل في وقت لوغاريتمي. من أجل أن تبقى حالة توازن ABL بعد كل إدخال ، يكون كل إدخال مصحوبًا بعملية موازنة . من أجل التنفيذ الفعال لهذه العملية ، تحتاج كل عقدة إلى تخزين معلومات الخدمة. للبساطة ، فقط حافظ على ارتفاع العقدة هناك.

 mutable struct AVLNode{K,V} # ,       255 # (  10^38 ) height::UInt8 key::K value::V left::Union{Nothing, AVLNode{K,V}} right::Union{Nothing, AVLNode{K,V}} parent::AVLNode{K,V} #   function AVLNode{K,V}() where {K,V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing return node end #    - function AVLNode{K,V}(key::SK, value::SV) where {K, V, SK<:K, SV<:V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end avlheight(node::Union{Nothing,AVLNode}) = node == nothing ? 0 : Int(node.height) 

إدراج سجل

يتم إجراء الإدراج الأساسي وفقًا للخوارزمية القياسية - انتقل إلى أسفل الشجرة لأسفل ، وابحث عن المكان الذي يمكنك فيه إدراج عقدة جديدة وإدراجها. سنقوم بكتابة الأغلفة للحصول على العقد الفرعية واستبدالها باستخدام الفهارس -1 و 1 بدلاً من اليسار واليمين:

 function child(root::AVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function insert_child!(root::AVLNode{K,V}, newnode::Union{Nothing,AVLNode{K,V}}, side::Signed) where {K,V} newnode == nothing || (newnode.parent = root) if side == -1 root.left = newnode elseif side == 1 root.right = newnode else throw(ArgumentError("Expecting side=-1 for inserting node to the left or side=1 for inserting to the right")) end end 

بعد ذلك ، ننطلق من الشجرة ونبحث عن انتهاكات للشروط 2 و 3. بعد ذلك ، ننظر في الخيارات التي قد تظهر (في الأشكال ، يشير اللون الأخضر إلى العقدة التي غيرت الارتفاع ، والعقدة التي تتم معالجتها هي أصلها).

القضية 0
بعد الإدراج ، أصبح ارتفاع العقدة مثل ارتفاع الأخت ، وواحد أقل من الارتفاع (القديم) للعقدة الأصل.

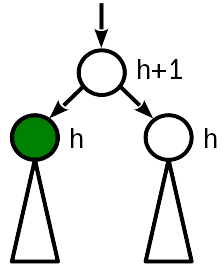
أفضل حالة ، لا تحتاج إلى لمس أي شيء آخر. أعلاه ، أيضا ، لم يعد بإمكانك المشاهدة ، لأن لن يتغير شيء هناك.

القضية 1
قبل الإدراج ، كان ارتفاع العقدة مساويًا لارتفاع عقدة الأخت. يرفع الإدراج جذر الشجرة الفرعية ، ويتم مقارنة ارتفاع العقدة بارتفاع الأصل.

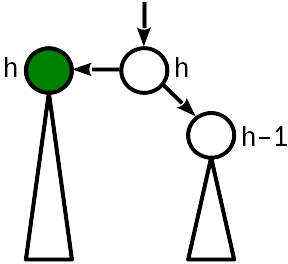
في هذه الحالة ، يكفي "رفع" العقدة الأصلية ، وزيادة طولها بمقدار 1. في الوقت نفسه ، تحتاج إلى الاستمرار في الانتقال إلى جذر الشجرة ، لأن تغيير ارتفاع العقدة الأصل قد يؤدي إلى انتهاك الشرط 2 بمستوى أعلى.

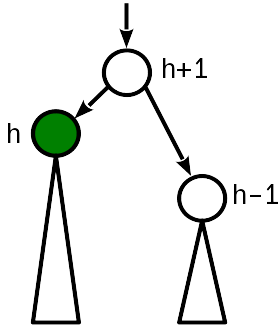
 fucntion promote!(nd::AVLNode, by::Integer=1) nd.height += by end fucntion demote!(nd::AVLNode, by::Integer=1) nd.height -= by end 

القضية 2

بعد الإدراج ، أصبح فرق الارتفاع مع الشجرة الفرعية 2 ، ثم "دفعت" الشجرة اليسرى إلى الأعلى:

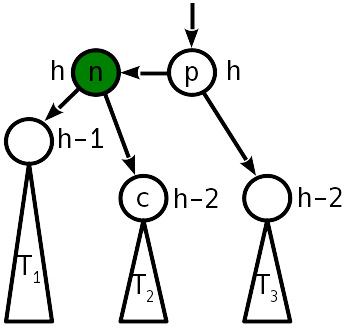
يتم التعامل مع المشكلة من خلال عملية تسمى "التناوب البسيط" التي تحول الشجرة على النحو التالي:

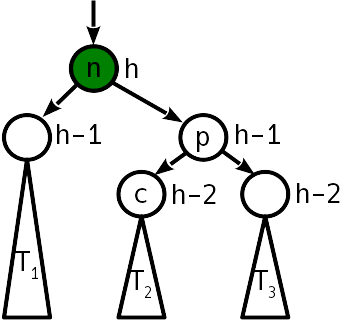
منعطف بسيط يتطلب 6 تغييرات المؤشر.

لاحظ أنه في الإسقاط على المحور الأفقي ، يظل ترتيب القمم n و p والأشجار T ₁ - T ₃ قبل وبعد الدوران كما هو. هذا هو تحقيق شرط الطلب. كما ترون ، بعد رفع الشجرة ، لم يعد التوازن مطلوبًا.

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end 

القضية 3
بعد الإدراج ، أصبح الفرق في الارتفاع مع الشجرة الفرعية 2 ، والشجرة اليمنى "دفعت" لأعلى:

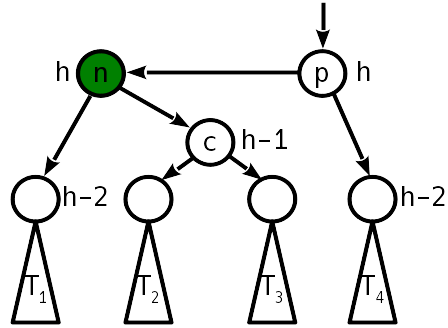
في هذه الحالة ، لن يساعد الدور المفرد البسيط ، ولكن يمكنك تشغيل منعطف بسيط لليسار حول المنحدر الأيمن ، الأمر الذي سيؤدي إلى الحالة 2 ، التي تتم معالجتها بالفعل مع انعطاف يمين بسيط.

لتقليل عدد "التفوق" في العقد ، يمكن دمج دورتين في عملية واحدة ، تسمى دورة كبيرة أو مزدوجة. بعد ذلك ، بدلاً من 12 تغييرًا من المؤشرات ، ستكون هناك حاجة إلى 10. فقط ، ونتيجة للدوران المزدوج ، تأخذ الشجرة النموذج التالي:

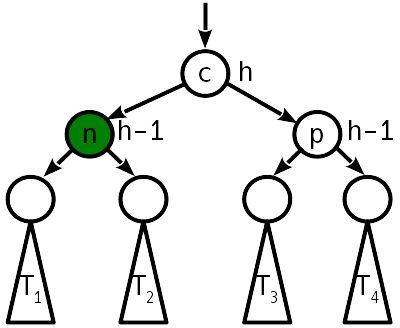
كما ترون ، بعد انعطاف مزدوج ، لا يلزم أيضًا تحقيق مزيد من التوازن للشجرة.

 # pivot       funtion double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end 

لذلك ، عند إدراج سجل في شجرة AVL ، فأنت بحاجة إلى تغييرات O (log ₂ N ) في المعلومات حول ارتفاع العقد وليس أكثر من عمليتي تدوير. الجمع بين كل شيء في وظيفة واحدة إدراج. سيختلف عن الإدراج الأساسي فقط في أنه بعد إدخال عقدة جديدة ، fix_insertion!() الدالة fix_insertion!() ، والتي تنتقل من العقدة التي تم إدراجها حديثًا إلى الجذر ، fix_insertion!() من التوازن وإذا لزم الأمر.

 function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 # true == 1, false == 0 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

تقوم fix_insertion!() بالتحقق من اختلاف الارتفاع بين عقدتين تابعتين ، بدءًا من العقدة الأصل من العقدة المدرجة. إذا كان يساوي 1 - نحن في الحالة 1 ، تحتاج إلى رفع ارتفاع العقدة والارتفاع. إذا كانت الصفر ، تكون الشجرة متوازنة. إذا كانت تساوي 2 - هذه هي الحالة 2 أو 3 ، فأنت بحاجة إلى تطبيق التدوير المناسب ، وتصل الشجرة إلى حالة متوازنة.

 #     -  , #   -  imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) #      0 - ..        while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 #       , # ..   dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end 

حذف السجل

الإزالة أصعب قليلاً من الإدخال.

للبدء ، فكر في الحذف المعتاد لإدخال من شجرة بحث ثنائية.

1. إذا كان السجل المحذوف موجودًا في الورقة ، فسيتم حذف السجل ببساطة ، كل شيء بسيط هنا.
2. إذا كان السجل المحذوف في عقدة تحتوي على سليل واحد فقط ، فسيتم وضع هذا السالب ، مع كل الشجرة الفرعية الخاصة به ، في مكان العقدة البعيدة.
3. إذا كان هناك اثنين من المتحدرين ، فسيتم البحث إما عن الحد الأقصى للعنصر في الشجرة الفرعية اليسرى أو في الحد الأدنى في الشجرة اليمنى (من خلال خاصية شجرة البحث ، تُضمن العقدة ذات العنصر الأقصى بعدم وجود سليل يمين ، مع وجود عنصر كحد أدنى لليسار ، وبالتالي يكون الحذف سهلاً) وضعت بدلا من السجل المحذوف.

ولكن بعد ذلك ، قد يكون توازن الشجرة مضطربًا ، لذا يجب عليك الصعود من أصل العقدة البعيدة ، واستعادتها. لاحظ أنه في البداية ، يُضمن أن أحد أحفاد الوالد المعني قد خفض الارتفاع بمقدار 1. ومع وضع ذلك في الاعتبار ، تحتاج إلى النظر في الخيارات (تظهر العقد التي غيرت الارتفاع باللون الأحمر ، والعقدة المعالجة هي الأصل من الأحمر):

القضية 1
صفر اختلال التوازن. لذلك ، قبل الإزالة ، كان 1 modulo ، والآن العقد التابعة هي 2 أقل من الأصل.

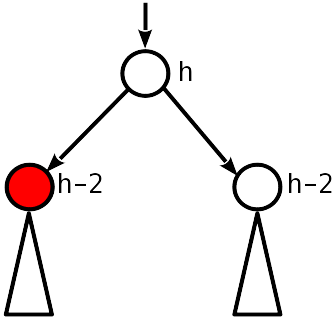
تحتاج إلى خفض العقدة الأصل بمقدار 1 ومتابعة التحرك لأعلى.

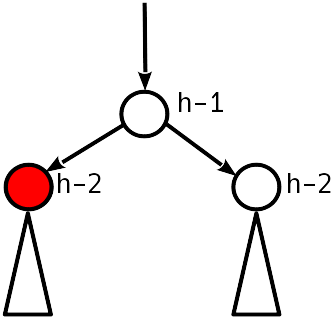
القضية 2
الخلل 1 معامل.

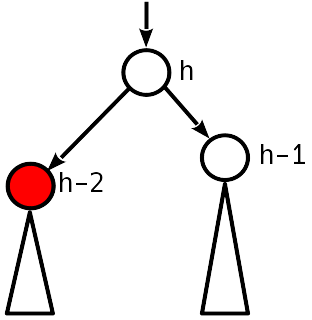
راض عن حالة AVL ، يمكنك التوقف.

القضية 3
الخلل 2 هو modulo ، العقدة الشقيقة للواحدة الهابطة لها اختلال غير صفري.

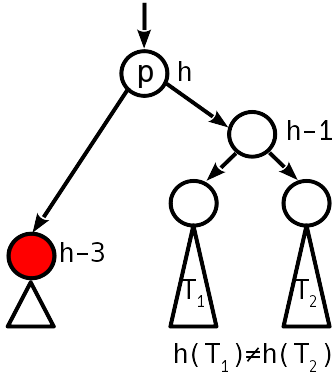
نستعيد التوازن عن طريق البساطة (إذا كان T ₁ أقل من T ₂ ) أو بالتناوب المزدوج (وإلا) ، كما حدث أثناء الإدراج. يتناقص ارتفاع الشجرة الفرعية ، أي قد يحدث انتهاك فوق الشجرة.

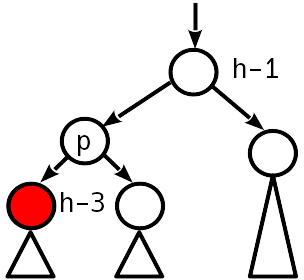
القضية 4
عدم التوازن 2 modulo ، العقدة الأخت لديه عدم توازن الصفر.

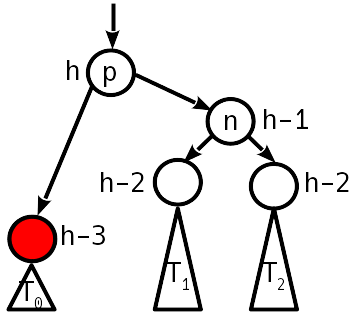
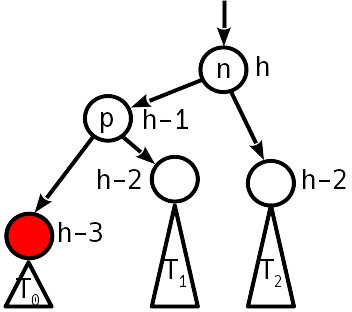
يعمل الدوران البسيط على استعادة حالة الموازنة ، بينما لا يتغير ارتفاع الشجرة الفرعية - نتوقف عن الصعود.

 function next_node(node::AVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::AVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::AVLNode) node = start skew = imbalance(node) while (node !== node.parent) && (abs(skew) != 1) if skew != 0 @assert abs(skew) == 2 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) < 2 if prev_skew == dir node = double_rotate!(child(n, dir), dir) else node = rotate!(n, dir) prev_skew != 0 || break end else node.height -= 1 end node = node.parent skew = imbalance(node) end end 

صعود وسقوط أشجار AVL

هناك ميزة ليست لطيفة للغاية من أشجار AVL الكلاسيكية هي صعوبة حذف سجل: التناوب يمكن أن "يعيد ضبط" الشجرة الفرعية بأكملها من مستوى واحد لأسفل ، ثم في أسوأ الحالات ، يتطلب الحذف تدوير شجرة O (سجل ₂ N ) - في كل مرة ترتفع فيها بمستوى واحد في fix_deletion!() .

بسبب هذا السلوك غير المقارب غير الجيد ، فإن أشجار AVL قد مهدت الطريق لأشجار حمراء سوداء ظهرت في سبعينيات القرن الماضي ولديها حالة توازن أضعف - المسار من الجذر إلى أبعد ورقة ليس أكثر من ضعف المسار من الجذر إلى أقرب ورقة. وبسبب هذا ، يكون ارتفاع الأشجار ذات اللون الأحمر الداكن في أسوأ الأحوال 2log ₂ N مقابل 1.44log ₂ N لأشجار AVL ، ولكن حذف سجل لا يتطلب أكثر من ثلاث دورات بسيطة. وبالتالي ، يُحتمل أن تفقد عمليات البحث والإدراج بسبب ارتفاع الشجرة في الأداء ، ولكن هناك ربح محتمل إذا تخللت عمليات الإدراج مع عمليات الحذف.

إضراب AVL

اتضح أن الخوارزمية "المثالية" لبناء أشجار البحث الثنائية يجب أن تضمن ارتفاعًا صغيرًا (على مستوى شجرة AVL الكلاسيكية) وعددًا ثابتًا من الدورات عند إضافة أو حذف سجل. لم يتم اختراع هذا بعد ، ولكن في عام 2015 تم نشر عمل اقترح هيكلًا يحسن خصائص كل من أشجار AVL والأحمر والأسود. تقع الفكرة بالقرب من أشجار AVL ، ولكن حالة التوازن مريحة للسماح بحذف السجلات بشكل أكثر كفاءة. يتم صياغة خصائص بنية تسمى "شجرة AVL ضعيفة" (W (eak) AVL tree) على النحو التالي:

1. الترتيب: بالنسبة لأي عقدة ، يكون المفتاح في أعلى الشجرة اليسرى أقل من المفتاح في أعلى الشجرة الفرعية اليمنى (إذا لم تكن أحفاد العقد فارغة).
2. ترتيب تصاعدي يتم تعيين كل عقدة رتبة. رتبة جميع العقد الفارغة هي صفر ، ورتبة الأوراق هي 1. رتبة العقدة الأصلية أكبر من رتبة الطفل.
3. ضعف توازن ABL: يختلف ترتيب العقدة عن رتبة العقد الفرعية بما لا يزيد عن 2.

اتضح أن مثل هذا الهيكل يشمل خصائص كل من أشجار AVL الكلاسيكية والأشجار الحمراء السوداء. على وجه الخصوص ، إذا أدخلنا الشرط المتمثل في أن العقدتين الفرعيتين لا يمكن أن تختلف عن الوالد في المرتبة بـ 2 ، فسوف نحصل على شجرة AVL منتظمة ، وسوف يتطابق الترتيب مع ارتفاع الشجرة الفرعية تمامًا.

جمال أشجار SAVL هو أن الضعف الطفيف لحالة AVL يسمح بتوازن الشجرة عند حذف سجل بما لا يزيد عن منعطفين! تقدير ارتفاع الشجرة هو h <min (1.44log ₂ M ، 2log ₂ N ) ، حيث N هو عدد الإدخالات في الشجرة ، M هو عدد الإدخالات ، مقارنة بـ h <2log ₂ N للأشجار ذات اللون الأحمر الأسود. , - , , .

- , . - .

.

-, "" "". , :

 mutable struct WAVLNode rank::UInt8 key::K value::V left::Union{Nothing, WAVLNode{K,V}} right::Union{Nothing, WAVLNode{K,V}} parent::WAVLNode{K,V} #   function WAVLNode{K,V}() where {K,V} node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing return node end #    - function WAVLNode{K,V}(key, value) where {K,V} key, value = convert(K, key), convert(V, value) node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end struct WAVLTree{K, V} entry::WAVLNode{K,V} WAVLTree{K,V}() where {K,V} = new{K,V}(WAVLNode{K,V}()) end function child(root::WAVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function Base.getindex(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) node = avlt.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

, -. : 1 , — , 0 ( ) 1 ( ). imbalance() , , .

 wavlrank(node::Union{Nothing,WAVLNode}) = node == nothing ? 0 : Int(node.rank) function imbalance(node::WAVLNode) rr, lr = wavlrank(node.right), wavlrank(node.left) skew = rr - lr diff = node.rank - max(rr, lr) skew, diff end 

, . , , , , -, - .

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end # pivot       function double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

, — -. .

0
, ..:

1. 1, 1
2. 0, 2 , .
   .

1
2 ( 0, 2 ).
1 .

2
1, 2.

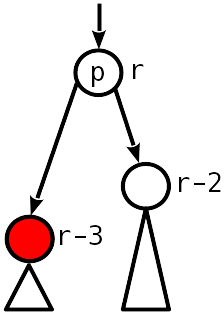
1, .

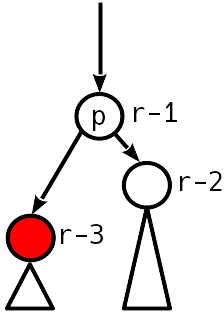
3
2 ( 1, .. ), 2 .

, . .

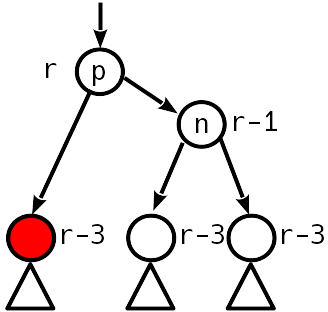
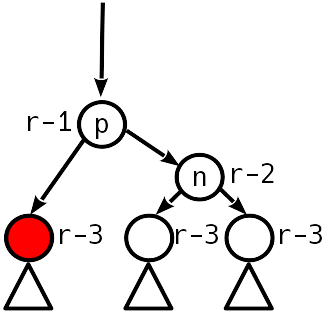
4

.

, , , .. .

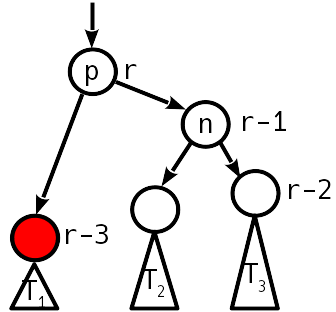
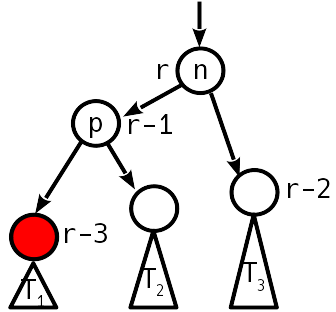
— T ₁ T ₂ , p 2, p 1.

5

.

, , .

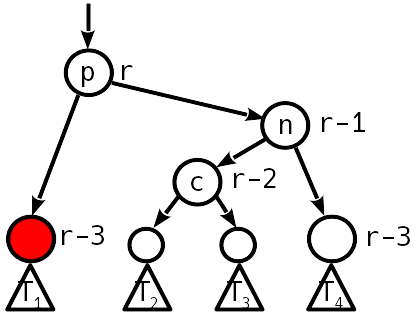
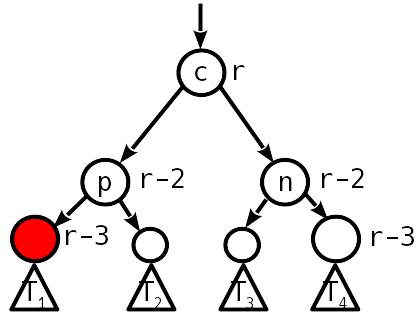
 function next_node(node::WAVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::WAVLNode) node = start skew, diff = imbalance(node) while (node !== node.parent) if skew == 0 if node.right == nothing node.rank = 1 else break end elseif abs(skew) == 1 if diff == 1 break else node.rank -= 1 end else dir = -skew ÷ 2 n = child(node, -dir) prev_skew, prev_diff = imbalance(n) if prev_diff == 2 @assert prev_skew == 0 n.rank -= 1 node.rank -= 1 elseif prev_skew == dir double_rotate!(child(n, dir), dir) break else rotate!(n, dir) break end end node = node.parent skew, diff = imbalance(node) end end 

-.

 julia> const wavl = WAVLTree{Int, Int}() julia> const avl = AVLTree{Int, Int}() julia> const dd = Dict{Int,Int}() julia> x = trues(1_000_000) #       ~  julia> for i = 1:1_000_000; dd[i] = avl[i] = wavl[i] = i * i; end julia> for i=1:500_000 k = rand(1:1_000_000) x[k] = false delete!(avl, k) delete!(wavl, k) delete!(dd, k) end # ,     julia> const y = Int[] julia> for i in eachindex(x); if x[i] push!(y, i); end; end julia> @btime let s = 0.0; for idx in y; s += dd[idx]; end; s; end 57.626 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += wavl[idx]; end; s; end 57.796 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += avl[idx]; end; s; end 53.884 ms (0 allocations: 0 bytes) 2.0238199367708794e17 

, , . , , - , -, .

— ?
— , . , , .

.

— , . n - . , , .. , .

*

— , " ", " ", " -", " ". , , -. . , .

*
** O (1), ...

, " — ". , . — ( ) , , , . .

*
** ,

استنتاج

() — , , , , , . — , .. , , .

مراجع

1. "-" nickme
2. Rank-Balanced Trees by Bernhard Haeupler, Siddhartha Sen, Robert E. Tarjan // ACM Transactions on Algorithms | June 2015, Vol 11(4) pdf
3. Goodrich MT, Tamassia R. Algorithm Design and Applications