مرحبا بالجميع! اكتشفت مؤخرا لغة الصدأ. شارك انطباعاته الأولى في مقال سابق . قررت الآن أن أعمق قليلاً ، لذلك تحتاج إلى شيء أكثر خطورة من القائمة. سقط خياري على شجرة ميركل. في هذا المقال أريد:
- نتحدث عن هذا الهيكل البيانات
- انظروا الى ما الصدأ بالفعل
- تقديم التنفيذ الخاص بك
- مقارنة الأداء
شجرة ميركل
هذا هيكل بيانات بسيط نسبيًا ، وهناك بالفعل الكثير من المعلومات حوله على الإنترنت ، لكنني أعتقد أن مقالي سيكون غير مكتمل بدون وصف للشجرة.
ما هي المشكلة
تم اختراع شجرة ميركل مرة أخرى في عام 1979 ، ولكنها اكتسبت شعبيتها بفضل blockchain. سلسلة الكتلة في الشبكة كبيرة جدًا (بالنسبة إلى عملة البيتكوين أكثر من 200 جيجابايت) ، وليس كل العقد يمكن أن تضخها. على سبيل المثال ، الهواتف أو سجلات النقد. ومع ذلك ، فهم بحاجة إلى معرفة حقيقة تضمين هذه المعاملة أو تلك في الكتلة. لهذا ، تم اختراع بروتوكول SPV - التحقق من الدفع المبسط .
كيف تعمل الشجرة؟
هذه شجرة ثنائية أوراقها تجزء من أي أشياء. لبناء المستوى التالي ، يتم أخذ تجزئة الأوراق المجاورة في أزواج ، متسلسلة ، ويتم حساب التجزئة من نتيجة التسلسل ، وهو موضح في الصورة في الرأس. وبالتالي ، فإن جذر الشجرة هو تجزئة لجميع الأوراق. إذا قمت بإزالة أو إضافة عنصر ، فسيتغير الجذر.
كيف تعمل الشجرة؟
امتلاك شجرة Merkle ، يمكنك بناء دليل على إدراج معاملة في كتلة كمسار من تجزئة المعاملة إلى الجذر. على سبيل المثال ، نحن مهتمون بالمعاملة Tx2 ، حيث سيكون الدليل هو (Hash3 ، Hash01). تستخدم هذه الآلية أيضًا في SPV. العميل فقط بتحميل رأس كتلة مع تجزئة لها. وبعد أن تم التعامل مع الفائدة ، طلب إثباتًا من عقدة تحتوي على السلسلة بأكملها. بعد ذلك يقوم بالتحقق ، بالنسبة إلى Tx2 سيكون:
hash(Hash01, hash(Hash2, Hash3)) = Root Hash
تتم مقارنة النتيجة مع جذر رأس الكتلة. هذا النهج يجعل من المستحيل تزوير الأدلة ، لأنه في هذه الحالة لا تتقارب نتيجة الاختبار مع محتويات الرأس.
التطبيقات التي توجد بالفعل
الصدأ هي لغة شابة ، ولكن العديد من إنجازات شجرة ميركل مكتوبة بالفعل عليها. إذا حكمنا من خلال Github ، في الوقت الحالي ، 56 ، هذا أكثر من C و C ++ مجتمعين. على الرغم من أن تطبيق Go يجعلهم يواجهون 80 تطبيقًا.
للمقارنة ، اخترت هذا التطبيق بعدد النجوم في المستودع.
تم بناء هذه الشجرة بالطريقة الأكثر وضوحًا ، وهي رسم بياني للكائنات. كما أشرت بالفعل ، فإن هذا النهج ليس صديقًا تمامًا للصدأ. على سبيل المثال ، لا يمكن إجراء اتصال ثنائي الاتجاه من الأطفال إلى أولياء الأمور.
بناء الأدلة يحدث من خلال البحث في العمق. إذا تم العثور على ورقة بها علامة التجزئة الصحيحة ، فإن المسار إلى ذلك سيكون النتيجة.
ما يمكن تحسينه
لم يكن من المثير للاهتمام بالنسبة لي أن أجري تنفيذًا بسيطًا (n + 1) ، لذلك فكرت في التحسين. رمز لبلدي ناقلات-ميركل شجرة على جيثب .
تخزين البيانات
أول ما يتبادر إلى الذهن هو تحويل الشجرة إلى صفيف. سيكون هذا الحل أفضل بكثير من حيث موضع البيانات: المزيد من مرات الوصول إلى ذاكرة التخزين المؤقت والتحميل المسبق بشكل أفضل. المشي حول الأشياء المنتشرة من الذاكرة يستغرق وقتًا أطول. حقيقة مريحة هي أن جميع التجزئة هي نفس الطول ، لأنه محسوبة بواسطة خوارزمية واحدة. ستبدو شجرة Merkle في المصفوفة كما يلي:

دليل
عند تهيئة الشجرة ، يمكنك إنشاء HashMap مع جميع فهارس الأوراق. وبالتالي ، عندما لا تكون هناك ورقة ، ليس من الضروري الالتفاف على الشجرة بأكملها ، وإذا وجدت ، يمكنك الذهاب إليها على الفور والارتقاء إلى الجذر ، وبناء دليل. في تنفيذي ، جعلت HashMap اختيارية.
سلسلة و هاشينج
يبدو أنه يمكن تحسين هنا؟ بعد كل شيء ، كل شيء واضح - تأخذ اثنين من التجزئة ، الغراء لهم وحساب تجزئة جديدة. ولكن الحقيقة هي أن هذه الوظيفة غير تبادلية ، أي hash (H0، H1) ≠ hash (H1، H0). لهذا السبب ، عند إنشاء الدليل ، عليك أن تتذكر أي جانب من العقدة المجاورة قيد التشغيل. هذا يجعل الخوارزمية أكثر صعوبة في التنفيذ ، ويضيف الحاجة إلى تخزين البيانات الزائدة عن الحاجة. كل شيء سهل الإصلاح ، ما عليك سوى فرز العقدتين قبل التجزئة. على سبيل المثال ، لقد استشهدت بـ Tx2 ، مع الأخذ في الاعتبار التبادلية ، سيبدو الشيك كما يلي:
hash(hash(Hash2, Hash3), Hash01) = Root Hash
عندما لا تقلق بشأن الطلب ، فإن خوارزمية التحقق تبدو كالتفاف بسيط لمجموعة:
pub fn validate(&self, proof: &Vec<&[u8]>) -> bool { proof[2..].iter() .fold( get_pair_hash(proof[0], proof[1], self.algo), |a, b| get_pair_hash(a.as_ref(), b, self.algo) ).as_ref() == self.get_root() }
العنصر صفر هو تجزئة الكائن المطلوب ، الأول هو جاره.
دعنا نذهب!
ستكون القصة غير مكتملة بدون مقارنة أداء ، الأمر الذي استغرقني عدة مرات أكثر من تنفيذ الشجرة نفسها. لهذه الأغراض ، استخدمت إطار المعيار . مصادر الاختبارات نفسها هنا . تتم جميع الاختبارات من خلال واجهة TreeWrapper ، والتي تم تنفيذها لكلا الموضوعين:
pub trait TreeWrapper<V> { fn create(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn find(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn validate(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); }
كل الأشجار تعمل مع نفس التشفير الدائري . أنا هنا لن أقارن بين المكتبات المختلفة. أخذت الأكثر شيوعا.
ككائنات تجزئة ، يتم استخدام سلاسل تم إنشاؤها عشوائيًا. تتم مقارنة الأشجار على صفائف بأطوال مختلفة: (500 ، 1000 ، 1500 ، 2000 ، 2500 3000). 2500 - 3000 هو العدد التقريبي للمعاملات في كتلة بيتكوين في الوقت الحالي.
في كل الرسوم البيانية ، يشير المحور X إلى عدد عناصر الصفيف (أو عدد المعاملات في الكتلة) ، ويمثل المحور Y متوسط الوقت لإكمال العملية في ميكروثانية. وهذا هو ، وأكثر ما هو أسوأ.
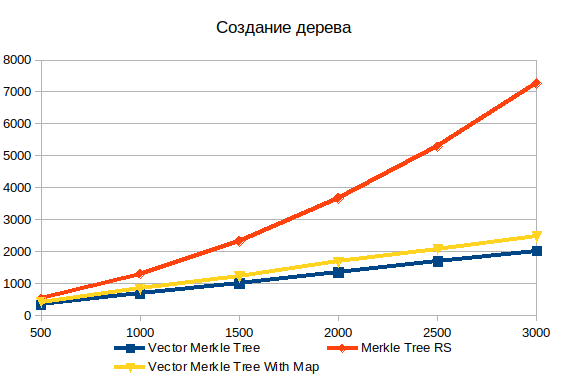
صنع شجرة
تخزين جميع البيانات شجرة في صفيف واحد يتجاوز إلى حد كبير الرسم البياني أداء الكائنات. لصفيف مع 500 عنصر ، 1.5 مرة ، و 3000 عنصر بالفعل 3.6 مرات. الطبيعة غير الخطية لاعتماد التعقيد على حجم بيانات الإدخال في التنفيذ القياسي واضحة للعيان.
أيضًا ، في المقابل ، أضفت نوعين مختلفين من شجرة المتجهات: مع وبدون HashMap . يضيف ملء بنية بيانات إضافية إلى حوالي 20٪ ، لكنه يسمح لك بالبحث عن الكائنات بشكل أسرع بكثير عند بناء الأدلة.
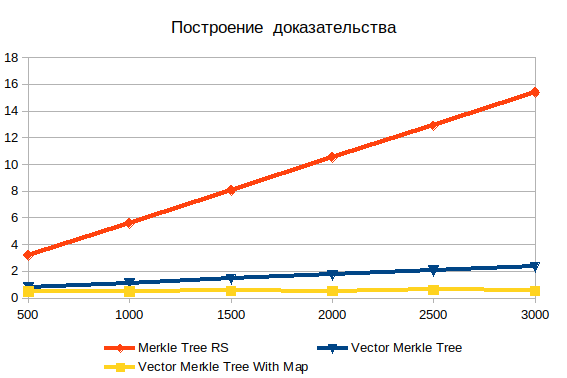
بناء الأدلة
هنا يمكنك أن ترى عدم كفاءة البحث بعمق. مع زيادة المدخلات ، يزداد الأمر سوءًا. من المهم أن نفهم أن الكائنات التي تبحث عنها عبارة عن أوراق ، لذلك لا يمكن أن يكون هناك تعقيد log (n) . إذا تم تجزئة البيانات مسبقًا ، يكون وقت التشغيل مستقلًا عمليًا عن عدد العناصر. بدون تجزئة ، ينمو التعقيد خطيًا ويتكون من بحث القوة الغاشمة.
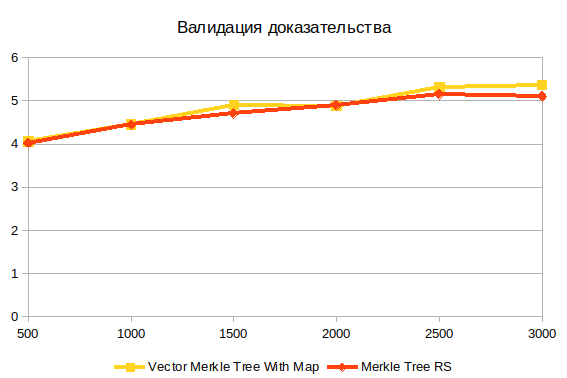
التحقق من صحة الأدلة
هذه هي العملية الأخيرة. لا يعتمد على هيكل الشجرة ، لأنه يعمل نتيجة لبناء الأدلة. أعتقد أن الصعوبة الرئيسية هنا هي حساب التجزئة.
يؤدي
- تؤثر طريقة تخزين البيانات بشكل كبير على الأداء. عندما يكون كل شيء في مجموعة واحدة أسرع بكثير. وتسلسل مثل هذا الهيكل سيكون في غاية البساطة. يتم تقليل المبلغ الإجمالي للكود أيضًا.
- يعمل تسلسل العقد مع الفرز على تبسيط التعليمات البرمجية بشكل كبير ، ولكنه لا يجعلها أسرع.
قليلا عن الصدأ
- أحب إطار المعيار . أنه يعطي نتائج واضحة مع القيم المتوسطة والانحرافات مجهزة الرسوم البيانية. قادرة على مقارنة تطبيقات مختلفة من نفس الرمز.
- قلة الميراث لا تتداخل بشكل كبير مع الحياة.
- وحدات الماكرو هي آلية قوية. لقد استخدمتها في اختبارات الشجرة الخاصة بي للمعلمات. أعتقد أنه إذا تم استخدامها بشكل سيئ ، فيمكنك فعل شيء لن تكون سعيدًا به فيما بعد.
- في بعض الأماكن ، يشعر المترجم بالملل من اختبارات الذاكرة الخاصة به. كان الافتراض المبدئي الخاص بي هو أن البدء بالكتابة في روست بكل بساطة لم ينجح.
مراجع