إذا كنت لا تكتب برنامجًا ، فلا تستخدم لغة البرمجة

Leslie Lampport هو مؤلف العمل الأساسي في الحوسبة الموزعة ، ويمكنك أيضًا معرفته بالحروف La in La TeX - "Lamport TeX". هذه هي المرة الأولى التي يقدم فيها مفهوم الاتساق الثابت مرة أخرى في عام 1979 ، وفاز مقالته "كيفية صنع حاسوب متعدد المعالجات ينفذ بشكل صحيح برامج متعددة المعالجات" بجائزة Dijkstra (وبشكل أكثر دقة ، في عام 2000 ، تم استدعاء الجائزة بالطريقة القديمة: "PODC Influential Paper Award" "). هناك مقال حول ويكيبيديا عنه حيث يمكنك الحصول على بعض الروابط الأكثر إثارة للاهتمام. إذا كنت متحمسًا لحل المشكلات قبل حدوثها أو مشاكل الجنرالات البيزنطيين (BFT) ، فعليك أن تفهم أن لامبورت وراء كل هذا.

هابراستاتيا هي ترجمة لتقرير ليزلي في منتدى هايدلبرغ الحائز على جائزة في عام 2018. سيركز الحديث على الأساليب الرسمية المستخدمة في تطوير أنظمة معقدة وحرجة مثل مسبار Rosetta space أو Amazon Amazon Services Services. يعد عرض هذا التقرير أمرًا ضروريًا لجلسة الأسئلة والأجوبة التي ستعقدها ليزلي في مؤتمر هيدرا - يمكن أن يوفر لك هاباستاتيا ساعة من الوقت لمشاهدة الفيديو. عند الانتهاء من هذه المقدمة ، ننقل الكلمة إلى المؤلف.

ذات مرة ، كتب توني هور: "كل برنامج كبير لديه برنامج صغير يحاول الخروج". أود أن أعيد صياغتها على النحو التالي: "في كل برنامج كبير ، هناك خوارزمية تحاول الخروج". ومع ذلك ، لا أعرف ما إذا كان توني سيوافق على هذا التفسير.

النظر ، على سبيل المثال ، الخوارزمية الإقليدية لإيجاد أكبر مقسوم مشترك لاثنين من الأعداد الصحيحة الموجبة $$$(م ، ن) دولا$ . في هذه الخوارزمية نسندها $$$x$ معنى $$$M$ . $$$N$ - القيمة $$$ذ$ ، ثم قم بطرح أصغر هذه القيم من الأكبر ، حتى تكون متساوية. معنى هذه $$$x$ و $$$ذ$ وسيكون أكبر عامل مشترك. ما هو الفرق الأساسي بين هذه الخوارزمية والبرنامج الذي ينفذها؟ في مثل هذا البرنامج سيكون هناك العديد من الأشياء منخفضة المستوى: $$$M$ و $$$N$ سيكون هناك نوع معين ، BigInteger أو شيء من هذا القبيل ؛ سيكون من الضروري تحديد سلوك البرنامج إذا $$$M$ و $$$N$ غير إيجابية؛ وهلم جرا وهكذا دواليك. لا يوجد فرق واضح بين الخوارزميات والبرامج ، ولكن على المستوى الحدسي نشعر بالفرق - الخوارزميات أكثر تجريدية ، ومستوى أعلى. وكما قلت ، داخل كل برنامج يعيش خوارزمية تحاول الخروج. عادة ما تكون هذه ليست الخوارزميات التي قيل لنا عنها في دورة الخوارزميات. كقاعدة عامة ، هذه خوارزمية مفيدة فقط لهذا البرنامج المحدد. في أغلب الأحيان ، سيكون الأمر أكثر تعقيدًا من تلك الموصوفة في الكتب. وغالبا ما تسمى هذه الخوارزميات المواصفات. وفي معظم الحالات ، تفشل هذه الخوارزمية ، لأن المبرمج لا يشك في وجودها. الحقيقة هي أنه لا يمكن رؤية هذه الخوارزمية إذا كان تفكيرك يركز على الكود ، على الأنواع ، الاستثناءات ، while الحلقات ، وأكثر من ذلك ، وليس على الخصائص الرياضية للأرقام. يصعب تصحيح البرنامج المكتوب بهذه الطريقة ، فماذا يعني تصحيح خوارزمية على مستوى التعليمات البرمجية. تم تصميم أدوات تصحيح الأخطاء للعثور على أخطاء في التعليمات البرمجية ، وليس في الخوارزمية. بالإضافة إلى ذلك ، سيكون مثل هذا البرنامج غير فعال ، لأنه ، مرة أخرى ، سوف تقوم بتحسين الخوارزمية على مستوى الرمز.

كما هو الحال في أي مجال آخر من مجالات العلوم والتكنولوجيا ، يمكن حل هذه المشكلات عن طريق وصفها رياضيا. هناك العديد من الطرق للقيام بذلك ، سننظر في أكثرها فائدة. وهو يعمل مع كل من الخوارزميات المتتابعة والمتوازية (الموزعة). تتكون هذه الطريقة في وصف تنفيذ الخوارزمية كسلسلة من الحالات ، ولكل ولاية تعيين خصائص للمتغيرات. على سبيل المثال ، توصف الخوارزمية الإقليدية كتسلسل للحالات التالية: أولاً ، يتم تعيين x القيمة M (رقم 12) ، و y هي القيمة N (رقم 18). ثم نطرح القيمة الأصغر من الأكبر ( $$$x$ من $$$ذ$ ) ، مما يؤدي بنا إلى الحالة التالية التي نتخذها بالفعل $$$ذ$ من $$$x$ ، وتنفيذ الخوارزمية يتوقف عند هذا: $$$[x \ leftarrow 12 ، \ leftarrow 18] ، [x \ leftarrow 12 ، \ leftarrow 6] ، [x \ leftarrow 6 ، \ leftarrow 6]$ .

نحن نسمي سلسلة من سلوك الدول وزوج من الحالات المتتالية خطوة. ثم يمكن وصف أي خوارزمية من خلال مجموعة متنوعة من السلوكيات التي تمثل جميع المتغيرات المحتملة للخوارزمية. لكل نموذج محدد M و N ، هناك تجسيد واحد فقط ، لذلك ، مجموعة من السلوك الواحد كافية لوصفه. الخوارزميات الأكثر تعقيدًا ، خاصة الخواص المتوازية ، لديها الكثير من السلوكيات.

يتم وصف العديد من السلوكيات ، أولاً ، عن طريق تقييم أولي للحالات (المسند مجرد دالة ذات قيمة منطقية) ؛ وثانيا ، مسند الحالة القادمة لأزواج الدول. بعض السلوك $$$s_1 ، s_2 ، s_3 ...$ يدخل في العديد من السلوكيات فقط إذا كان المسند الأولي صحيحًا $$$s_1$ و مسوحات الحالة التالية صحيحة لكل خطوة $$$(s_i، s_ {i + 1})$ . دعونا نحاول وصف الخوارزمية الإقليدية بهذه الطريقة. المسند الأولي هنا هو: $$$(x = M) \ land (y = N)$ . ويتم وصف مسند الحالة التالية لأزواج الحالات بالصيغة التالية:

من فضلك لا تشعر بالقلق - فهناك ستة سطور فقط ؛ من السهل للغاية معرفة ما إذا كنت تفعل ذلك بالترتيب. في هذه الصيغة ، تشير المتغيرات بدون حدود إلى الحالة الأولى ، والمتغيرات ذات الحدود هي نفس المتغيرات في الحالة الثانية.

كما ترى ، يشير السطر الأول إلى أن x في الحالة الأولى أكبر من y في الحالة الأولى. بعد AND المنطقي ، يُذكر أن قيمة x في الحالة الثانية تساوي قيمة x في الحالة الأولى مطروحًا منها قيمة y في الحالة الأولى. بعد منطقية AND أخرى ، يتم ذكر أن قيمة y في الحالة الثانية تساوي قيمة y في الحالة الأولى. كل هذا يعني أنه في حالة أكبر من x على y ، سيقوم البرنامج بطرح y من x وترك y بدون تغيير. تصف الأسطر الثلاثة الأخيرة الحالة عندما تكون y أكبر من x. لاحظ أن هذه الصيغة خاطئة إذا كانت x تساوي y. في هذه الحالة ، لا توجد الحالة التالية ، ويتوقف السلوك.

لذلك ، لقد وصفنا للتو الخوارزمية الإقليدية في صيغتين رياضيتين - ولم يكن علينا أن نعبث بأي لغة برمجة. ماذا يمكن أن يكون أكثر جمالا من هاتين الصيغتين؟ استبدالها مع صيغة واحدة. سلوك $$$s_1 ، s_2 ، s_3 ...$ هو تنفيذ الخوارزمية الإقليدية فقط إذا:

• $$$Init_E$ صحيح ل $$$s_1$ .
• $$$Next_E$ صحيح لكل خطوة $$$(s_i، s_ {i + 1})$ .

يمكن كتابة هذا كمسند للسلوكيات (سوف نسميها خاصية) على النحو التالي. يمكن التعبير عن الشرط الأول ببساطة $$$Init_E$ . هذا يعني أننا نفسر حالة المسند على أنه صحيح بالنسبة للسلوك فقط إذا كان صحيحًا بالنسبة إلى الحالة الأولى. الشرط الثاني هو مكتوب على النحو التالي: $$$\ square Next_E$ . مربع يعني المراسلات بين مسند أزواج الدولة ومسندات السلوك ، أي $$$Next_E$ صحيح لكل خطوة في السلوك. نتيجة لذلك ، تبدو الصيغة كما يلي: $$$Init_E \ land \ square Next_E$ .

لذلك ، كتبنا الخوارزمية الإقليدية رياضيا. في جوهرها ، هذه ببساطة تعاريف أو اختصارات لـ $$$Init_E$ و $$$Next_E$ . هذه الصيغة كاملة ستبدو كما يلي:

ليست هي جميلة؟ لسوء الحظ ، بالنسبة للعلم والتكنولوجيا ، ليس الجمال معيارًا محددًا ، لكن هذا يعني أننا نسير على الطريق الصحيح.

الخاصية التي قمنا بتدوينها صحيحة بالنسبة لبعض السلوكيات فقط في حالة استيفاء الشرطين اللذين وصفناهما للتو. في $$$M = 12 دولا$ و $$$N = 18 دولا$ أنها صحيحة للسلوك التالي: $$$[x \ leftarrow 12 ، \ leftarrow 18] ، [x \ leftarrow 12 ، \ leftarrow 6] ، [x \ leftarrow 6 ، \ leftarrow 6]$ . لكن هذه الشروط مستوفاة أيضًا للإصدارات الأقصر من نفس السلوك: $$$[x \ leftarrow 12 ، \ leftarrow 18] ، [x \ leftarrow 12 ، \ leftarrow 6]$ . ويجب ألا نأخذها في الاعتبار ، حيث إنها مجرد خطوات منفصلة للسلوك الذي أخذناه بالفعل في الاعتبار. هناك طريقة واضحة للتخلص منها: ببساطة تجاهل السلوكيات التي تنتهي في حالة تكون فيها الخطوة التالية واحدة على الأقل ممكنة. ولكن هذا ليس هو النهج الصحيح ، نحن بحاجة إلى حل أكثر عمومية. بالإضافة إلى ذلك ، هذا الشرط لا يعمل دائما.

مناقشة هذه المشكلة تقودنا إلى مفاهيم الأمن والنشاط. تشير خاصية الأمان إلى الأحداث التي تكون صالحة. على سبيل المثال ، يُسمح للخوارزمية بإرجاع القيمة الصحيحة. تشير خاصية النشاط إلى الأحداث التي يجب أن تحدث عاجلاً أم آجلاً. على سبيل المثال ، يجب أن ترجع الخوارزمية بعض القيمة عاجلاً أم آجلاً. بالنسبة إلى خوارزمية الإقليدية ، تكون خاصية الأمان كما يلي: $$$Init_E \ land \ square Next_E$ . يجب إضافة خاصية نشاط إلى هذا لمنع الإيقاف المبكر: $$$Init_E \ land \ square Next_E \ land L$ . في لغات البرمجة ، في أفضل الأحوال ، هناك بعض التعريف البدائي للنشاط. في معظم الأحيان ، لم يتم ذكر النشاط حتى ، إنه يعني ضمنيًا أن الخطوة التالية في البرنامج يجب أن تحدث. ولإضافة هذه الخاصية ، تحتاج إلى رمز معقد إلى حد ما. من الناحية الرياضية ، من السهل جدًا التعبير عن النشاط (هناك حاجة إلى ذلك المربع فقط لهذا الغرض) ، لكن لسوء الحظ ، ليس لدي وقت لذلك - سيتعين علينا أن نقصر مناقشتنا على الأمن.

استطراد صغير فقط لعلماء الرياضيات: كل خاصية هي مجموعة من السلوكيات التي تكون هذه الخاصية صحيحة. لكل مجموعة من التسلسلات ، هناك طوبولوجيا طبيعية تنشئها وظيفة المسافة التالية:

$$$s = 17 ، \ sqrt {2} ، -2 ، \ pi ، 10 ، 1/2 \\ t = 17 ، \ sqrt {2} ، -2 ، e ، 10 ، 1/$

المسافة بين هاتين الوظيفتين هي ¼ ، لأن الفرق الأول بينهما في العنصر الرابع. وفقًا لذلك ، كلما كان الجزء الذي تتطابق فيه هذه التسلسلات أطول ، كلما كان أقرب إلى بعضها البعض. هذه الوظيفة في حد ذاتها ليست مثيرة للاهتمام للغاية ، ولكنها تخلق طوبولوجيا مثيرة جدًا للاهتمام. في هذا الهيكل ، خصائص الأمان عبارة عن مجموعات مغلقة ، وخصائص النشاط عبارة عن مجموعات كثيفة. في الطوبولوجيا ، تنص إحدى النظريات الأساسية على أن كل مجموعة هي تقاطع مجموعة مغلقة ومجموعة كثيفة. إذا تذكرنا أن الخصائص عبارة عن مجموعات من السلوكيات ، فسيتبع من هذه النظرية أن كل خاصية هي عبارة عن تزامن بين خاصية أمان وخاصية نشاط. هذا هو الاستنتاج الذي سيكون مثيرا للاهتمام للمبرمجين كذلك.

يعني التصحيح الجزئي أنه لا يمكن إيقاف البرنامج إلا إذا أعطى الإجابة الصحيحة. تقول الدقة الجزئية للخوارزمية الإقليدية إنها إذا أكملت التنفيذ ، إذن $$$x = GCD (M، N)$ . ولدينا الخوارزمية يكمل تنفيذ إذا $$$x = y$ . وبعبارة أخرى ، $$$(x = y) \ Rightarrow (x = GCD (M، N))$ . تعني الصحة الجزئية لهذه الخوارزمية أن هذه الصيغة صحيحة لجميع حالات السلوك. أضف رمزًا إلى بدايته $$$\ مربع$ مما يعني "لجميع الخطوات". كما ترون ، لا توجد متغيرات ذات حد في الصيغة ، لذلك تعتمد حقيقتها على الحالة الأولى في كل خطوة. وإذا كان هناك شيء صحيح بالنسبة للحالة الأولى من كل خطوة ، فسيكون هذا البيان صحيحًا لجميع الحالات. يتم الإرضاء الجزئي للخوارزمية الإقليدية بأي سلوك مقبول للخوارزمية. كما رأينا ، فإن السلوك مسموح به إذا كانت الصيغة المقدمة للتو صحيحة. عندما نقول أن العقار راضٍ ، فهذا يعني ببساطة أن هذه الخاصية تتبع بعض الصيغة. أليس هذا رائعا؟ ومن هنا:

$$$Init_E \ land \ square Next_E \ Rightarrow \ square ((x = y) \ Rightarrow (x = GCD (M، N)))$

ننتقل إلى الثبات. المربع ذو الأقواس بعد تسميته خاصية الثبات :

$$$Init_E \ land \ square Next_E \ Rightarrow \ colour {red} {\ square ((x = y) \ Rightarrow (x = GCD (M، N)))}$

تسمى القيمة الموجودة بين قوسين بعد المربع المربع الثابت :

$$$Init_E \ land \ square Next_E \ Rightarrow \ square (\ color {red} {(x = y) \ Rightarrow (x = GCD (M، N))})$

كيف تثبت الثبات؟ لإثبات $$$Init_E \ land \ square Next_E \ Rightarrow \ square I_E$ ، تحتاج إلى إثبات ذلك لأي سلوك $$$s_1 ، s_2 ، s_3 ...$ النتيجة $$$Init_E \ land \ square Next_E$ هي الحقيقة $$$I_e$ لأي شرط $$$s_j$ . يمكننا إثبات ذلك عن طريق الاستقراء ، لذلك نحتاج إلى إثبات ما يلي:

1. من $$$Init_E \ land \ square Next_E$ يتبع ذلك $$$I_e$ صحيح بالنسبة للدولة $$$s_1$ .
2. من $$$Init_E \ land \ square Next_E$ يتبع ذلك إذا $$$I_e$ صحيح بالنسبة للدولة $$$s_j$ بعد ذلك أيضا
   صحيح بالنسبة للدولة $$$s_ {j + 1}$ .

أولا نحن بحاجة لإثبات ذلك $$$Init_E$ الوسائل $$$I_e$ . لأن الصيغة تدعي ذلك $$$Init_E$ صحيح بالنسبة للدولة الأولى ، وهذا يعني ذلك $$$I_e$ صحيح بالنسبة للدولة الأولى. كذلك ، متى $$$Next_E$ صحيح لأي خطوة ، و $$$I_e$ وفيا ل $$$s_j$ . $$$I_e$ صحيح ل $$$s_ {j + 1}$ لأن $$$\ square Next_E$ يعني ذلك $$$Next_E$ صحيح لأي زوج من الدول. هذا مكتوب مثل هذا: $$$Next_E \ land I_E \ Rightarrow I_E$ حيث $$ هل هذا $$$I_e$ لجميع المتغيرات مع السكتة الدماغية.

يسمى الثابت الذي يفي بالشرطين اللذين أثبتناهما للتو بأنه ثابت حثي . صحة جزئية ليست حثي. لإثبات ثباتها ، تحتاج إلى العثور على الثابت الاستقرائي الذي يعني ذلك. في حالتنا ، فإن الثابت الاستقرائي سيكون على النحو التالي: $$ .

يعتمد كل إجراء لاحق من الخوارزمية على حالته الحالية ، وليس على الإجراءات السابقة. تفي الخوارزمية بخاصية الأمان ، حيث يتم الاحتفاظ بالثابت الاستقرائي فيها. تستطيع خوارزمية إقليديا حساب أكبر قاسم مشترك (بمعنى أنه لا يتوقف حتى يتم الوصول إليه) نظرًا لحقيقة أنه يحتوي على ثابت $$ . لفهم الخوارزمية ، تحتاج إلى معرفة ثابت الاستقرائي. إذا درست التحقق من البرنامج ، فأنت تعلم أن دليل المتغير الذي تم تقديمه للتو ليس أكثر من وسيلة لإثبات صحة جزئية لبرامج Floyd-Hoare المتسلسلة. قد تكون سمعت أيضًا عن طريقة Hoviki - Gris ، وهي امتداد لأسلوب Floyd-Hoar للبرامج الموازية. في كلتا الحالتين ، يتم كتابة الثابت الاستقرائي باستخدام شرح البرنامج. وإذا قمت بذلك بمساعدة الرياضيات ، وليس باستخدام لغة برمجة ، يتم ذلك بكل بساطة. هذا هو ما يكمن في صميم طريقة Hoviki Gris. تجعل الرياضيات الظواهر المعقدة سهلة الوصول إلى فهم ، على الرغم من أن الظواهر نفسها ، بالطبع ، لن تصبح أكثر بساطة.

نلقي نظرة فاحصة على الصيغ. إذا في الرياضيات كتبنا صيغة مع المتغيرات $$$x$ و $$$ذ$ ، هذا لا يعني أن المتغيرات الأخرى غير موجودة. يمكنك إضافة معادلة أخرى فيها $$$ذ$ وضعت فيما يتعلق $$$z$ ، لن يغير شيئا. فقط الصيغة لا تقول شيئًا عن أي متغيرات أخرى. لقد قلت بالفعل أن الحالة عبارة عن تخصيص للقيم للمتغيرات ، والآن يمكنك إضافتها إلى هذا: مع كل المتغيرات المحتملة ، تبدأ $$$x$ و $$$ذ$ وتنتهي مع سكان إيران. يجب أن أعترف: عندما قلت أن الصيغة $$$Init_E \ land \ square Next_E$ يصف الخوارزمية الإقليدية ، لقد كذبت. في الواقع يصف الكون الذي المعاني $$$x$ و $$$ذ$ تمثل تنفيذ الخوارزمية الإقليدية. الجزء الثاني من الصيغة ( $$$\ square Next_E$ ) يدعي أن كل خطوة تتغير $$$x$ أو $$$ذ$ . بعبارة أخرى ، يصف الكون الذي لا يستطيع سكان إيران تغييره إلا إذا تغير المعنى $$$x$ أو $$$ذ$ . ويترتب على ذلك أنه لا يمكن أن يولد أحد في إيران بعد إتمام خوارزمية إقليدس. من الواضح ، هذا ليس كذلك. يمكن تصحيح هذا الخطأ إذا كان لدينا خطوات صالحة من أجلها $$$x$ و $$$ذ$ تبقى دون تغيير. لذلك ، نحتاج إلى إضافة جزء آخر إلى صيغتنا: $$$Init_E \ land \ square (Next_E \ lor (x '= x) \ land (y' = y))$ . للإيجاز ، نكتبها هكذا: $$$Init_E \ land \ square [Next_E] _ {<x، y>}$ . هذه الصيغة تصف الكون الذي يحتوي على خوارزمية الإقليدية. يجب إجراء نفس التغييرات في دليل المتغير:

• نثبت: $$$Init_E \ land \ colour {red} {\ square [Next_E] _ {<x، y>}} \ Rightarrow \ square I_E$
• بمساعدة:
  
  1. $$$Init_E \ Rightarrow I_E$
  2. $$$\ colour {red} {\ square [Next_E] _ {<x، y>}} \ land I_E \ Rightarrow I'_E$

هذا التغيير مسؤول عن أمان الخوارزمية الإقليدية ، نظرًا لأن السلوكيات أصبحت ممكنة في الوقت الحالي $$$x$ و $$$ذ$ لا تتغير. يجب التخلص من هذه السلوكيات باستخدام خاصية النشاط. هذا بسيط للغاية ، لكنني لم أتحدث عنه الآن.

التحدث عن التنفيذ. لنفترض أن لدينا نوعًا من الآلات التي تنفذ الخوارزمية الإقليدية مثل الكمبيوتر. يمثل الأرقام صفائف من الكلمات 32 بت. لعمليات بسيطة من الجمع والطرح ، تحتاج إلى العديد من الخطوات ، مثل الكمبيوتر. إذا لم تلمس النشاط بعد ، فيمكننا أيضًا تخيل مثل هذه الآلة من خلال الصيغة $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ . ماذا نعني عندما نقول أن الآلة الإقليدية تنفذ الخوارزمية الإقليدية؟ هذا يعني أن الصيغة التالية صحيحة:

لا تشعر بالذعر ، سنقوم الآن بفحصه بالترتيب. تقول أن الجهاز يلبي بعض الممتلكات ( $$$\ Rightarrow$ ). هذه الخاصية هي الصيغة الإقليدية. $$$(Init_E \ land \ square [Next_E] _ {<x، y>}$ ، النقاط هي التعبيرات التي تحتوي على متغيرات الجهاز Euclidean ، و $$$مع$ هو بديل. بمعنى آخر ، السطر الثاني هو الصيغة الإقليدية التي فيها $$$x$ و $$$ذ$ استبدال النقاط. في الرياضيات ، لا يوجد رمز مقبول عالميًا للاستبدال ، لذلك كان علي أن أتوصل إليه بنفسي. في الأساس ، الصيغة الإقليدية ( $$$Init_E \ land \ square [Next_E] _ {<x، y>}$ ) هو اختصار للصيغة:

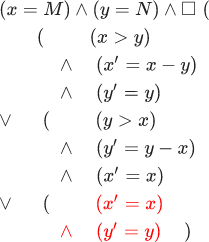
الضوء الأحمر جزء من الصيغة ، والسماح $$$x$ و $$$ذ$ في $$$(Init_E \ land \ square [Next_E] _ {\ color {red} {<x، y>}}$ ابقى كما هو

لا يوضح التعبير الموصوف أن الجهاز يقوم بتنفيذ الخوارزمية الإقليدية فحسب ، بل إنه أيضًا يقوم بذلك مع مراعاة البدائل المحددة. إذا كنت تأخذ اثنين فقط من البرامج وتقول إن متغيرات هذه البرامج مرتبطة بها $$$x$ و $$$ذ$ - ليس من المنطقي القول إن كل هذا "ينفذ الخوارزمية الإقليدية". من الضروري الإشارة بدقة إلى كيفية تنفيذ الخوارزمية ولماذا تصبح الصيغة صحيحة بعد كل التباديل. الآن ليس لدي وقت لإظهار أن التعريف الموضح أعلاه صحيح ، يجب أن تأخذ كلامي من أجله. لكنك ، كما أعتقد ، قدرت بالفعل مدى بساطتها وأنيقتها. الرياضيات جميلة حقًا - باستخدامها تمكنا من تحديد معنى أن خوارزمية تنفذ أخرى.

لإثبات ذلك ، من الضروري إيجاد ثابت مناسب $$$I_ {ME}$ السيارات الإقليدية. للقيام بذلك ، يجب أن تتحقق الشروط التالية:

1. $$$Init_ {ME} \ Rightarrow (Init_E ، WITH \ thinspace x \ leftarrow ... ، y \ leftarrow ...)$
2. $$$I_ {ME} \ land [Next_ {ME}] _ {<...>} \ Rightarrow ([Next_E] _ {<x، y>}، WITH \ thinspace x \ leftarrow ...، y \ leftarrow. ..)$

لن نتطرق إليها الآن ، فقط انتبه إلى حقيقة أن هذه الصيغ الرياضية العادية ، وإن لم تكن أبسطها. ثابتة $$$I_ {ME}$ يشرح لماذا تنفذ الآلة الإقليدية الخوارزمية الإقليدية. التنفيذ يعني استبدال التعبيرات للمتغيرات. هذه عملية رياضية شائعة جدًا. ولكن في البرنامج ، لا يمكن إجراء مثل هذا الاستبدال. لا يمكنك استبدال a + b بدلاً من x في تعبير المهمة x = … ، فلن يكون لهذا السجل معنى. ثم كيف لتحديد أن أحد البرامج ينفذ آخر؟ إذا كنت تعتقد فقط من حيث البرمجة ، فإن هذا غير ممكن. في أفضل الأحوال ، يمكنك العثور على تعريف صعب ، ولكن هناك طريقة أفضل بكثير تتمثل في ترجمة البرامج إلى صيغ رياضية واستخدام التعريف الذي قدمته أعلاه. ترجمة البرنامج إلى صيغة رياضية تعني إعطاء دلالات البرنامج. إذا كان الجهاز الإقليدي هو برنامج ، و $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ - تدوينها الرياضي ، إذن $$$(Init_E \ land \ square [Next_E] _ {<x، y>} ، مع \ thinspace x \ leftarrow ... ، y \ leftarrow ...)$ يوضح لنا أن هذا يعني أن "البرنامج ينفذ الخوارزمية الإقليدية." لغات البرمجة معقدة للغاية ، لذا فإن ترجمة البرنامج إلى لغة رياضيات معقدة أيضًا ، لذا فنحن في الواقع لا نفعل ذلك. ببساطة ، لغات البرمجة ليست مصممة لكتابة الخوارزميات عليها. , , , : , x y , . , , , .

- : , , , . , . — . . , . , — , . :

. $$$DecrementX$ :

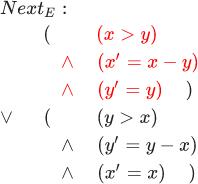
— $$$DecrementY$ :

, :

.

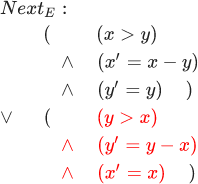
. Rosetta — , . Virtuoso. . TLA+, . , , . , (Eric Verhulst), . , TLA+, : « TLA+ . - C. TLA+ Virtuoso». . . , , , . . TLA+. , .

. Communications of the ACM ] , - Amazon . Amazon Web Services — , Amazon. , — TLA+. . -, , . , , . -, , . , — , , . -, , Amazon , . , 10% TLA+.

— Microsoft. TLA+ 2004 . 2015 TLA+, . . Amazon Web Services. Microsoft , , . : « , ». , Microsoft - . : « ». 2016-17 . TLA+, 150 , Azure ( Microsoft). Azure 2018 , , . : « , . , ». , , . - : , . , , .

, TLA+ . , TLA+, TLA+ Azure, , TLA+. , . , TLA+ , . Microsoft Cosmos DB, , . , . TLA+, , , TLA+.

TLA+ — . . TLA+ . , , . TLA+ , . : TLA+ , .

, . , , . , . Amazon Microsoft , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .