ليس سراً أن أحد التساليات المفضلة لمطور البرامج هو إجراء مقابلات مع أصحاب العمل. نحن جميعا نفعل هذا من وقت لآخر ولأسباب مختلفة تماما. والأكثر وضوحا منهم - البحث عن وظيفة - أعتقد ، ليست هي الأكثر شيوعا. تعد حضور مقابلة طريقة جيدة للحفاظ على لياقتك البدنية وتكرار الأساسيات المنسية وتعلم شيء جديد. وإذا نجحت ، قم أيضًا بزيادة الثقة بالنفس. لقد شعرنا بالملل ، وضعنا أنفسنا في حالة "مفتوحة للعروض" في نوع من الشبكات الاجتماعية "التجارية" مثل
"LinkedIn" - ويقوم جيش مديري الموارد البشرية بمهاجمة صناديق البريد الوارد لدينا بالفعل للرسائل الواردة.

في هذه العملية ، وبينما يجري كل هذا السرير ، نواجه العديد من الأسئلة التي ، كما يقولون على الجانب الآخر من الستارة المنهارة ضمنيًا ، "تطوق الجرس" ، وتفاصيلها مخبأة وراء
ضباب الحرب . غالبًا ما يتم استرجاعها فقط في الاختبارات التي تجريها الخوارزميات وهياكل البيانات (شخصيًا ، لم يكن لدي مثل هذه البيانات على الإطلاق) وفي الواقع مقابلات.
واحدة من الأسئلة الأكثر شيوعا في مقابلة لمبرمج من أي تخصص هي القوائم. على سبيل المثال ، قوائم مرتبطة منفردة. والخوارزميات الأساسية ذات الصلة. على سبيل المثال ، منعطف. وعادة ما يحدث هذا بطريقة ما مثل هذا: "جيد ، ولكن كيف يمكنك توسيع قائمة مرتبطة منفردة؟" الشيء الرئيسي هو اللحاق مقدم الطلب على حين غرة بهذا السؤال.
في الواقع ، كل هذا دفعني إلى كتابة هذا الاستعراض القصير للتذكير المستمر والتنوير. لذلك ، النكات جانبا ، ها!
قائمة مرتبطة منفردة
قائمة مرتبطة هي واحدة من
هياكل البيانات الأساسية. يتكون كل عنصر (أو عقدة) منه ، في الواقع ، من البيانات المخزنة والروابط إلى العناصر المجاورة. تقوم القائمة المرتبطة منفردة بتخزين الرابط للعنصر التالي في البنية فقط ، بينما تحتفظ القائمة
ذات الارتباط المزدوج بالعنصر التالي والسابق. يسمح هذا التنظيم للبيانات بتحديد موقعه في أي منطقة ذاكرة (على سبيل المثال ،
صفيف ، يجب أن تكون جميع عناصره موجودة في الذاكرة واحدة تلو الأخرى).
هناك الكثير مما يمكن قوله حول القوائم ، بالطبع: يمكن أن تكون دائرية (أي العنصر الأخير يخزن رابطًا للعنصر الأول) أو لا (أي لا يوجد رابط للعنصر الأخير). يمكن كتابة القوائم ، أي تحتوي على بيانات من نفس النوع أم لا. وهلم جرا وهكذا دواليك.
أفضل محاولة كتابة بعض التعليمات البرمجية. على سبيل المثال ، بطريقة ما يمكنك تخيل عقدة قائمة:
final class Node<T> { let payload: T var nextNode: Node? init(payload: T, nextNode: Node? = nil) { self.payload = payload self.nextNode = nextNode } }
"عام" هو نوع قادر على تخزين الحمولات
payload من أي نوع في حقل
payload .
يتم تعريف القائمة نفسها بشكل شامل بواسطة العقدة الأولى:
final class SinglyLinkedList<T> { var firstNode: Node<T>? init(firstNode: Node<T>? = nil) { self.firstNode = firstNode } }
تم إعلان العقدة الأولى اختيارية ، لأن القائمة قد تكون فارغة.
من الناحية النظرية ، بالطبع ، في الفصل الدراسي ، تحتاج إلى تنفيذ جميع الطرق اللازمة - إدراج ، حذف ، الوصول إلى العقد ، وما إلى ذلك ، لكننا سنفعل ذلك في وقت آخر. في الوقت نفسه ، سوف نتحقق مما إذا كان استخدام struct (التي تشجعنا عليها Apple بنشاط من خلال مثالنا) هو الخيار الأفضل ، وربما نتذكر نهج "النسخ عند الكتابة" .انتشار قائمة واحدة مرتبطة
الطريقة الأولى دورة
لقد حان الوقت للانضمام إلى العمل الذي نحن هنا اليوم! والطريقة الأكثر فعالية للتعامل معها هي طريقتان. الأول هو حلقة بسيطة ، من الأولى إلى العقدة الأخيرة.
تعمل الدورة مع ثلاثة متغيرات يتم تعيين قيمة للعقدة السابقة والحالية والتالية قبل البداية. (في هذه اللحظة ، تكون قيمة العقدة السابقة فارغة بشكل طبيعي.) تبدأ الدورة بالتحقق من أن العقدة التالية ليست فارغة ، وإذا كان الأمر كذلك ، فسيتم تنفيذ نص الدورة. لا يحدث أي سحر في الحلقة: في العقدة الحالية ، يتم تعيين ارتباط للحقل السابق على الحقل الذي يشير إلى العنصر التالي (في التكرار الأول ، تتم إعادة تعيين قيمة الارتباط ، على التوالي ، والتي تتوافق مع حالة الشؤون في العقدة الأخيرة). إضافة إلى ذلك ، يتم تعيين قيم جديدة للمتغيرات المقابلة للعقدة السابقة والحالية والتالية. بعد الخروج من الحلقة ، يتم تعيين العقدة الحالية (أي آخر يمكن تكراره بشكل عام) قيمة ارتباط جديدة للعقدة التالية ، لأن يحدث الخروج من الحلقة في الوقت الحالي عندما تصبح العقدة الأخيرة في القائمة حالية.
بكلمات ، بالطبع ، يبدو كل هذا غريبًا وغير مفهوم ، لذلك من الأفضل النظر إلى الكود:
extension SinglyLinkedList { func reverse() { var previousNode: Node<T>? = nil var currentNode = firstNode var nextNode = firstNode?.nextNode while nextNode != nil { currentNode?.nextNode = previousNode previousNode = currentNode currentNode = nextNode nextNode = currentNode?.nextNode } currentNode?.nextNode = previousNode firstNode = currentNode } }
للتحقق ، نستخدم قائمة العقد التي حمولاتها هي معرفات
عدد صحيح بسيط. إنشاء قائمة من عشرة عناصر:
let node = Node(payload: 0)
يبدو أن كل شيء على ما يرام ، لكننا أشخاص ، وليسوا أجهزة كمبيوتر ، وسيكون من الجميل لنا الحصول على دليل مرئي على صحة القائمة التي تم إنشاؤها والخوارزمية الموضحة أعلاه. ربما ستكون طباعة بسيطة كافية. لجعل الإخراج قابلاً للقراءة ، أضف تطبيق بروتوكول
CustomStringConvertible العقدة باستخدام معرف عدد صحيح:
extension Node: CustomStringConvertible where T == Int { var description: String { let firstPart = """ Node \(Unmanaged.passUnretained(self).toOpaque()) has id \(payload) and """ if let nextNode = nextNode { return firstPart + " next node \(nextNode.payload)." } else { return firstPart + " no next node." } } }
... والقائمة المقابلة لعرض جميع العقد بالترتيب:
extension SinglyLinkedList: CustomStringConvertible where T == Int { var description: String { var description = """ List \(Unmanaged.passUnretained(self).toOpaque()) """ if firstNode != nil { description += " has nodes:\n" var node = firstNode while node != nil { description += (node!.description + "\n") node = node!.nextNode } return description } else { return description + " has no nodes." } } }
سيحتوي تمثيل سلسلة أنواعنا على عنوان في الذاكرة ومعرف صحيح. باستخدامها ، نقوم بتنظيم طباعة القائمة التي تم إنشاؤها من عشرة عقد:
print(String(describing: list))
قم بتوسيع هذه القائمة وطباعتها مرة أخرى:
list.reverse() print(String(describing: list))
قد تلاحظ أن العناوين الموجودة في ذاكرة القائمة والعقد لم تتغير ، ويتم طباعة العقد بالترتيب العكسي. تشير الإشارات إلى العنصر التالي من العقدة الآن إلى العنصر السابق (على سبيل المثال ، العنصر التالي من العقدة "5" ليس الآن "6" ، ولكن "4"). وهذا يعني أننا فعلنا ذلك!
الطريقة الثانية. العودية
تعتمد الطريقة الثانية المعروفة للقيام بدورها على
التكرار . لتنفيذه ، سنعلن عن وظيفة تأخذ العقدة الأولى من القائمة ، وتُرجع العقدة الأولى "الجديدة" (التي كانت الأخيرة من قبل).
المعلمة وقيمة الإرجاع اختيارية ، لأنه داخل هذه الوظيفة يتم استدعاؤها مرارًا وتكرارًا على كل عقدة لاحقة حتى تكون فارغة (أي حتى الوصول إلى نهاية القائمة). وفقًا لذلك ، في نص الوظيفة ، من الضروري التحقق مما إذا كانت العقدة التي تسمى الوظيفة فارغة وما إذا كانت هذه العقدة تحتوي على ما يلي. إذا لم يكن كذلك ، فستقوم الدالة بإرجاع ما تم تمريره إلى الوسيطة.
في الواقع ، حاولت بصراحة وصف الخوارزمية الكاملة بالكلمات ، لكن في النهاية قمت بمسح كل شيء تقريبًا ، لأن النتيجة ستكون مستحيلة الفهم. لرسم مخططات انسيابية ووصف خطوات الخوارزمية رسميًا - أيضًا ، في هذه الحالة ، أعتقد أن هذا غير منطقي ، لأنه سيكون أكثر ملاءمة لك وللي للقراءة فقط ومحاولة فهم كود
Swift :
extension SinglyLinkedList { func reverseRecursively() { func reverse(_ node: Node<T>?) -> Node<T>? { guard let head = node else { return node } if head.nextNode == nil { return head } let reversedHead = reverse(head.nextNode) head.nextNode?.nextNode = head head.nextNode = nil return reversedHead } firstNode = reverse(firstNode) } }
يتم "التفاف" الخوارزمية نفسها بطريقة من نوع القائمة الفعلية ، لراحة الاتصال.
يبدو أقصر ، ولكن ، في رأيي ، يصعب فهمه.
نطلق على هذه الطريقة نتيجة الحيز السابق ونطبع نتيجة جديدة:
list.reverseRecursively() print(String(describing: list))
يمكن أن نرى من الإخراج أن جميع العناوين في الذاكرة لم تتغير مرة أخرى ، والعقد تتبع الآن بالترتيب الأصلي (أي ، "تم نشرها" مرة أخرى). وهذا يعني أننا حصلنا على حق مرة أخرى!
النتائج
إذا نظرت إلى أساليب الانعكاس بعناية (أو أجريت تجربة مع حساب المكالمات) ، ستلاحظ أن الحلقة في الحالة الأولى والطريقة الداخلية (العودية) في الحالة الثانية تحدث مرة واحدة أقل من عدد العقد في القائمة (في حالتنا ، تسعة الوقت). يمكنك أيضًا الانتباه إلى ما يحدث حول الحلقة في الحالة الأولى - نفس تسلسل المهام - ونداء الطريقة الأولى غير التكرارية في الحالة الثانية. اتضح أنه في كلتا الحالتين يتم تكرار "الدائرة" عشر مرات بالضبط للحصول على قائمة من عشر عقد. وبالتالي ، لدينا
تعقيد خطي لكلتا الخوارزميات -
O (n) .
بشكل عام ، تعتبر الخوارزميات الموصوفة الأكثر فاعلية لحل هذه المشكلة. بالنسبة للتعقيد الحسابي ، لا يمكن الخروج بخوارزمية ذات قيمة أقل: بطريقة أو بأخرى ، تحتاج إلى "زيارة" كل عقدة لتعيين قيمة جديدة للقيمة المخزنة داخل الرابط.
ميزة أخرى تجدر الإشارة إليها هي "تعقيد الذاكرة المخصصة". كلا الخوارزميات المقترحة تنشئ عددًا ثابتًا من المتغيرات الجديدة (ثلاثة في الحالة الأولى وواحدة في الثانية). هذا يعني أن مقدار الذاكرة المخصصة لا يعتمد على الخصائص الكمية لبيانات الإدخال ويتم وصفها بوظيفة ثابتة - O (1).
ولكن ، في الواقع ، في الحالة الثانية هذا ليس كذلك. خطر العودية هو أن يتم تخصيص ذاكرة إضافية لكل مكالمة متكررة على
المكدس . في حالتنا ، فإن عمق العودية يتوافق مع كمية البيانات المدخلة.
وأخيراً ، قررت أن أجرب أكثر من ذلك بقليل: بطريقة بسيطة وبدائية قمت بقياس وقت التنفيذ المطلق لطريقتين لكمية مختلفة من بيانات الإدخال. مثل هذا:
let startDate = Date().timeIntervalSince1970
وهذا ما حصلت عليه (هذه هي البيانات الأولية من
الملعب ):
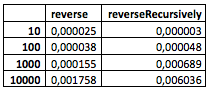
(لسوء الحظ ، لم يتقن جهاز الكمبيوتر الخاص بي القيم الأكبر.)
ما يمكن رؤيته من الجدول؟ لا شيء خاص بعد. على الرغم من أنه من الملاحظ بالفعل أن الطريقة العودية تتصرف بشكل أسوأ قليلاً مع وجود عدد صغير نسبياً من العقد ، ولكن في مكان ما بين 100 و 1000 تبدأ في الظهور بشكل أفضل.
كما جربت نفس الاختبار البسيط داخل مشروع
"Xcode" كامل. النتائج هي كما يلي:

أولاً ، تجدر الإشارة إلى أنه تم الحصول على النتائج بعد تنشيط وضع التحسين "العدواني" الذي يهدف إلى سرعة التنفيذ (
-Ofast ) ، وهذا جزئيًا ما يجعل الأرقام صغيرة جدًا. ومن المثير للاهتمام أيضًا أن الطريقة العودية أظهرت في هذه الحالة نفسها أفضل قليلاً ، على العكس ، وفقط في أحجام صغيرة جدًا من بيانات الإدخال ، وفقدت الطريقة بالفعل على قائمة من 100 عقدة. من بين 100000 ، قام بإنهاء البرنامج بشكل غير طبيعي.
استنتاج
لقد حاولت تغطية موضوع كلاسيكي إلى حد ما من وجهة نظر لغتي البرمجة المفضلة في الوقت الحالي ، وآمل أن تكون فضولي لمتابعة التقدم وكذلك أنا. وأنا سعيد جدًا إذا تمكنت من تعلم شيء جديد أيضًا - ثم ضيعت وقتي بالتأكيد في هذا المقال (بدلاً من الجلوس ومشاهدة
البرامج التلفزيونية ).
إذا كانت لدى شخص ما رغبة في تتبع نشاطي الاجتماعي ، فإليك رابطًا إلى "Twitter" ، حيث يوجد أولاً روابط إلى مشاركاتي الجديدة وأكثر من ذلك بقليل.