إذا كان من المرجح أن يتم نشر المقال السابق ، فقد حان الوقت لاختبار قدرات التوازي لجوليا على جهازها.
متعدد النواة أو المعالجة الموزعة
يتم توفير تطبيق الحوسبة المتوازية مع الذاكرة الموزعة بواسطة الوحدة النمطية Distributed كجزء من المكتبة القياسية المتوفرة مع جوليا. تحتوي معظم أجهزة الكمبيوتر الحديثة على أكثر من معالج واحد ، ويمكن تجميع العديد من أجهزة الكمبيوتر. يتيح لك استخدام قوة هذه المعالجات المتعددة إجراء العديد من العمليات الحسابية بشكل أسرع. يتأثر الأداء بعاملين رئيسيين: سرعة المعالجات نفسها وسرعة الوصول إلى الذاكرة الخاصة بهم. في المجموعة ، من الواضح أن وحدة المعالجة المركزية هذه سيكون لها الوصول الأسرع إلى ذاكرة الوصول العشوائي على نفس الكمبيوتر (العقدة). ولعل الأمر الأكثر إثارة للدهشة هو أن هذه المشكلات وثيقة الصلة بالكمبيوتر المحمول النموذجي متعدد النواة بسبب الاختلافات في سرعة الذاكرة الرئيسية وذاكرة التخزين المؤقت. لذلك ، يجب أن تسمح لك بيئة المعالجة المتعددة الجيدة بالتحكم في "ملكية" جزء من الذاكرة بواسطة معالج محدد. توفر Julia بيئة متعددة المعالجات تعتمد على المراسلة والتي تسمح للبرامج بالعمل في وقت واحد على عمليات متعددة في مجالات ذاكرة مختلفة.
يختلف تطبيق المراسلة في جوليا عن البيئات الأخرى ، مثل MPI [1] . عادة ما يكون التواصل في جوليا "أحادي الاتجاه" ، مما يعني أن المبرمج يحتاج إلى التحكم صراحة في عملية واحدة فقط في عملية ثنائية العملية. بالإضافة إلى ذلك ، لا تبدو هذه العمليات عادةً "إرسال رسالة" و "تلقي رسالة" ، ولكنها تشبه عمليات المستوى الأعلى ، مثل المكالمات إلى الوظائف المعرفة من قبل المستخدم.
البرمجة الموزعة في جوليا مبنية على أساسين: الروابط عن بعد والمكالمات عن بُعد . الارتباط البعيد هو كائن يمكن استخدامه من أي عملية للإشارة إلى كائن مخزّن في عملية معينة. المكالمة عن بُعد هي طلب لعملية واحدة لاستدعاء وظيفة معينة وفقًا لوسيطات معينة لعملية أخرى (ربما تكون هي نفسها).
الروابط البعيدة تأتي في شكلين: Future و RemoteChannel .
مكالمة عن بعد بإرجاع Future ويقوم بذلك على الفور ؛ تستمر العملية التي أجرت المكالمة في التشغيل التالي ، بينما تتم المكالمة عن بُعد في مكان آخر. يمكنك الانتظار حتى تكتمل المكالمة عن بعد باستخدام أمر الانتظار Future المرتجع ، ويمكنك أيضًا الحصول على القيمة الكاملة للنتيجة باستخدام الجلب .
من ناحية أخرى ، لدينا RemoteChannels التي يتم إعادة كتابتها. على سبيل المثال ، يمكن أن تنسق العديد من العمليات معالجتها ، مع الإشارة إلى نفس القناة البعيدة. كل عملية لها معرف المرتبطة. تحتوي العملية التي توفر مطالبة جوليا التفاعلية دائمًا على معرف 1. العمليات التي يتم استخدامها افتراضيًا للعمليات المتزامنة تسمى "العمال". عند وجود عملية واحدة فقط ، تعتبر العملية 1 عملية. خلاف ذلك ، فإن جميع العمليات بخلاف العملية 1 تعتبر عمال.

دعنا ننكب على ذلك. julia -pn مع julia -pn بوستسكريبت يوفر سير العمل n على الكمبيوتر المحلي. عادة ما يكون من المنطقي أن n تساوي عدد مؤشرات ترابط وحدة المعالجة المركزية (النوى المنطقية) على الجهاز. لاحظ أن الوسيطة -p تقوم ضمنيًا بتحميل الوحدة النمطية الموزعة.
كيف تبدأ الحاشية؟يجب أن تكون عمليات وحدة التحكم واضحة لمستخدمي Linux ، بما في ذلك. هذا البرنامج التعليمي مخصص لمستخدمي Windows عديمي الخبرة.
يوفر Julia Terminal (REPL) القدرة على استخدام أوامر النظام:
julia> pwd() # "C:\\Users\\User\\AppData\\Local\\Julia-1.1.0" julia> cd("C:/Users/User/Desktop") # julia> run(`calc`) # # Windows. # Process(`calc`, ProcessExited(0))
باستخدام هذه الأوامر ، يمكنك بدء جوليا من جوليا ، لكن من الأفضل عدم الانطلاق
سيكون من الأصح تشغيل cmd من julia / bin / وتشغيل الأمر julia -p 2 هناك أو خيار لعشاق التشغيل من اختصار: على سطح المكتب ، قم بإنشاء مستند المفكرة بالمحتويات التالية C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 ( حدد العنوان وعدد العمليات ) وحفظه كمستند نصي يحمل الاسم run.bat . هنا ، يوجد الآن على سطح مكتبك ملف نظام إطلاق Julia لـ 4 مراكز.
يمكنك استخدام طريقة أخرى (خاصة ذات صلة بـ Jupyter ):
using Distributed addprocs(2)
$ ./julia -p 2 julia> r = remotecall(rand, 2, 2, 2) Future(2, 1, 4, nothing) julia> s = @spawnat 2 1 .+ fetch(r) Future(2, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.18526 1.50912 1.16296 1.60607
الوسيطة الأولى إلى remotecall هي الوظيفة المدعوة.
لا تشير معظم البرامج المتزامنة في جوليا إلى عمليات محددة أو عدد العمليات المتاحة ، لكن الاتصال عن بعد يعتبر واجهة منخفضة المستوى توفر تحكمًا أكثر دقة.
الوسيطة الثانية إلى remotecall هي معرف العملية التي ستقوم بالعمل ، وسيتم تمرير الوسائط المتبقية إلى الوظيفة المطلوبة. كما ترون ، في الصف الأول ، طلبنا من العملية 2 بناء مصفوفة عشوائية 2 × 2 ، وفي الصف الثاني طلبنا إضافة 1 إليها. تتوفر نتيجة كلا الحسابين في مستقبلين ، r و s. الماكرو spawnat بتقييم التعبير في الوسيطة الثانية للعملية المحددة في الوسيطة الأولى. في بعض الأحيان قد تحتاج إلى قيمة محسوبة عن بعد. يحدث هذا عادة عندما تقرأ من كائن بعيد للحصول على البيانات اللازمة للعملية المحلية التالية. هناك وظيفة remotecall_fetch لهذا remotecall_fetch . هذا يعادل fetch (remotecall (...)) ، ولكن أكثر كفاءة.
تذكر أن getindex(r, 1,1) يعادل r[1,1] ، لذلك تستدعي هذه المكالمة العنصر الأول من المستقبل r .
remotecall المكالمة عن بُعد remotecall مناسب بشكل خاص. الماكرو @spawn يجعل @spawn أسهل. تعمل مع تعبير وليس وظيفة ، وتختار مكان إجراء العملية لك:
julia> r = @spawn rand(2,2) Future(2, 1, 4, nothing) julia> s = @spawn 1 .+ fetch(r) Future(3, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.38854 1.9098 1.20939 1.57158
لاحظ أننا استخدمنا 1 .+ Fetch(r) بدلاً من 1 .+ r هذا لأننا لا نعرف مكان تنفيذ الشفرة ، لذلك في الحالة العامة قد يكون من الضروري إحضار الانتقال r إلى عملية الإضافة. في هذه الحالة ، يكون @ spawn ذكيًا بما يكفي لإجراء العمليات الحسابية للعملية التي تمتلك r ، لذلك لن يكون الجلب جاهزًا للعمل (لم يتم تنفيذ أي عمل). (تجدر الإشارة إلى أن التفرخ ليس مدمجًا ، ولكن يتم تعريفه في جوليا على أنه ماكرو. يمكنك تحديد مثل هذه التراكيب الخاصة بك.)
من المهم أن تتذكر أنه بعد الاستخراج ، سوف تقوم Future بتخزين قيمته مؤقتًا محليًا. لا تستلزم المكالمات الإضافية التي يتم جلبها حدوث قفزة في الشبكة. بعد أن يتم تحديد كل العقود المستقبلية للإحالة ، يتم حذف القيمة المخزنة المحذوفة.
يشبه @spawn ، لكنه يدير المهام فقط في العملية المحلية. نستخدمها لإنشاء مهمة "تغذية" لكل عملية. تحدد كل مهمة الفهرس التالي ، الذي يجب حسابه ، ثم تنتظر إكمال العملية وتتكرر حتى نفاد الفهارس.
لاحظ أن مهام وحدة التغذية لا تبدأ حتى تصل المهمة الرئيسية إلى نهاية كتلة @ sync ، وبعد ذلك تمر بالتحكم وتنتظر استكمال جميع المهام المحلية قبل العودة من الوظيفة.
بالنسبة إلى الإصدار v0.7 والإصدارات الأحدث ، يمكن لمهام التغذية مشاركة الحالة من خلال nextidx ، لأن كل هذه المهام يتم تنفيذها في نفس العملية. حتى إذا تم التخطيط للمهام معًا ، فقد يكون الحظر مطلوبًا في بعض السياقات ، مثل I / O غير المتزامن. هذا يعني أن تبديل السياق يحدث فقط في نقاط محددة جيدًا: في هذه الحالة ، عندما يتم remotecall_fetch . هذا هو الوضع الحالي للتنفيذ ، وقد يتغير في الإصدارات المستقبلية من Julia ، حيث إنه مصمم ليكون قادرًا على إكمال حتى N مهام في عمليات M أو M: N Threading . نحتاج بعد ذلك إلى نموذج للحصول على / تحرير الأقفال لـ nextidx ، لأنه من غير الآمن السماح لعدة عمليات بقراءة وكتابة الموارد في نفس الوقت.
يجب أن يكون الرمز متاحًا لأي عملية تقوم بتشغيله. على سبيل المثال ، في موجه Julia ، اكتب ما يلي:
julia> function rand2(dims...) return 2*rand(dims...) end julia> rand2(2,2) 2×2 Array{Float64,2}: 0.153756 0.368514 1.15119 0.918912 julia> fetch(@spawn rand2(2,2)) ERROR: RemoteException(2, CapturedException(UndefVarError(Symbol("#rand2")) Stacktrace: [...]
عرفت العملية 1 الوظيفة rand2 ، لكن العملية 2 لم تعرف. في معظم الأحيان ، سوف تقوم بتنزيل الكود من الملفات أو الحزم ، وسيكون لديك مرونة كبيرة في التحكم في العمليات التي تقوم بتحميل الكود. خذ بعين الاعتبار ملف DummyModule.jl يحتوي على التعليمات البرمجية التالية:
module DummyModule export MyType, f mutable struct MyType a::Int end f(x) = x^2+1 println("loaded") end
للإشارة إلى MyType في جميع العمليات ، يجب تحميل DummyModule.jl في كل عملية. استدعاء include ('DummyModule.jl') لعملية واحدة فقط. لتحميله في كل عملية ، استخدم الماكرو @everywhere (قم بتشغيل Julia مع julia -p 2):
julia> @everywhere include("DummyModule.jl") loaded From worker 3: loaded From worker 2: loaded
كالمعتاد ، هذا لا يجعل DummyModule متاحًا لأي عملية تتطلب الاستخدام أو الاستيراد. علاوة على ذلك ، عندما يتم تضمين DummyModule في نطاق عملية واحدة ، لا يتم تضمينه في أي عملية أخرى:
julia> using .DummyModule julia> MyType(7) MyType(7) julia> fetch(@spawnat 2 MyType(7)) ERROR: On worker 2: UndefVarError: MyType not defined ⋮ julia> fetch(@spawnat 2 DummyModule.MyType(7)) MyType(7)
ومع ذلك ، لا يزال من الممكن ، على سبيل المثال ، إرسال MyType إلى العملية التي قامت بتحميل DummyModule ، حتى لو لم يكن في النطاق:
julia> put!(RemoteChannel(2), MyType(7)) RemoteChannel{Channel{Any}}(2, 1, 13)
يمكن أيضًا تحميل الملف مسبقًا في العديد من العمليات عند بدء التشغيل باستخدام علامة -L ، ويمكن استخدام البرنامج النصي للتحكم في العمليات الحسابية:
julia -p <n> -L file1.jl -L file2.jl driver.jl
تحتوي عملية Julia التي تقوم بتشغيل برنامج التشغيل في المثال أعلاه على معرف 1 ، تمامًا مثل العملية التي توفر الموجه التفاعلي. أخيرًا ، إذا لم يكن DummyModule.jl ملفًا منفصلاً ، ولكن حزمة ، فسيؤدي استخدام DummyModule إلى تحميل DummyModule.jl في جميع العمليات ، ولكن نقله فقط إلى نطاق العملية التي تم استدعاء الاستخدام.
إطلاق وإدارة سير العمل
يحتوي تثبيت Julia الأساسي على دعم مدمج لنوعين من المجموعات:
- الكتلة المحلية المحددة مع الخيار -p ، كما هو موضح أعلاه.
- آلات الكتلة باستخدام خيار ملف - آلة. يستخدم هذا تسجيل الدخول ssh بدون كلمة مرور لبدء سير عمل Julia (على نفس المسار مثل المضيف الحالي) على الأجهزة المحددة.

تتوفر الوظائف الإضافية ، و rmprocs ، والعامل ، وغيرها كأداة برمجية لإضافة العمليات وإزالتها والاستعلام عنها في مجموعة.
julia> using Distributed julia> addprocs(2) 2-element Array{Int64,1}: 2 3
يجب أن يتم تحميل الوحدة النمطية Distributed بشكل صريح في العملية الرئيسية قبل استدعاء addprocs . يصبح تلقائيًا متاحًا لسير العمل. لاحظ أن العمال لا يقومون بتشغيل البرنامج النصي لبدء التشغيل ~/.julia/config/startup.jl ولا يقومون بمزامنة حالتهم العالمية (مثل المتغيرات العالمية وتعريفات الطرق الجديدة والوحدات النمطية المحمّلة) مع أي من العمليات الأخرى قيد التشغيل. يمكن دعم أنواع أخرى من المجموعات عن طريق كتابة ClusterManager الخاصة بك ، كما هو موضح أدناه في قسم ClusterManager .
إجراءات البيانات
يشكل إرسال الرسائل والبيانات المنقولة معظم النفقات العامة في برنامج موزع. يعد تقليل عدد الرسائل ومقدار البيانات المرسلة أمرًا بالغ الأهمية لتحقيق الأداء وقابلية التوسع. لهذا ، من المهم أن نفهم حركة البيانات التي تقوم بها مختلف بنى جوليا البرمجة الموزعة.
يمكن اعتبار عملية fetch عملية واضحة لنقل البيانات ، حيث إنها تطلب مباشرة نقل كائن إلى الجهاز المحلي. @spawn (والعديد من التركيبات ذات الصلة) بنقل البيانات أيضًا ، ولكن هذا ليس واضحًا جدًا ، لذلك يمكن أن يطلق عليه عملية نقل البيانات الضمنية. فكر في هذين النهجين لإنشاء مصفوفة عشوائية وتربيعها:
مرات الطريق:
julia> A = rand(1000,1000); julia> Bref = @spawn A^2; [...] julia> fetch(Bref);
الطريقة الثانية:
julia> Bref = @spawn rand(1000,1000)^2; [...] julia> fetch(Bref);
الفرق يبدو تافهاً ، لكنه في الحقيقة مهم للغاية بسبب سلوك @spawn . في الطريقة الأولى ، يتم بناء مصفوفة عشوائية محليًا ، ثم يتم إرسالها إلى عملية أخرى ، حيث يتم تربيعها. في الطريقة الثانية ، يتم بناء مصفوفة عشوائية وتربيعها في عملية أخرى. لذلك ، الأسلوب الثاني يرسل بيانات أقل بكثير من الأولى. في مثال اللعب هذا ، من السهل التمييز بين الطريقتين واختيارهما. ومع ذلك ، في برنامج حقيقي ، يمكن أن يكون تصميم حركة البيانات مكلفًا للغاية وربما بعض القياس.
على سبيل المثال ، إذا كانت العملية الأولى تحتاج إلى مصفوفة A ، فقد تكون الطريقة الأولى أفضل. أو ، إذا كانت الحوسبة A مكلفة وتستخدم العملية الحالية فقط ، فقد يكون نقلها إلى عملية أخرى أمرًا لا مفر منه. أو ، إذا كانت العملية الحالية لديها القليل جدًا من القواسم المشتركة بين fetch(Bref) ، فقد يكون من الأفضل التخلص من التزامن تمامًا. أو تخيل أن rand(1000, 1000) استبداله بعملية أكثر تكلفة. بعد ذلك ، قد يكون من المنطقي إضافة بيان spawn آخر لهذه الخطوة فقط.
المتغيرات العالمية
يمكن أن تشير التعبيرات المنفذة عن بعد من خلال التفرخ ، أو عمليات الإغلاق المحددة للتنفيذ عن بعد باستخدام remotecall ، إلى المتغيرات العامة. تتم معالجة الارتباطات العالمية في الوحدة النمطية Main بشكل مختلف قليلاً عن الارتباطات العالمية في الوحدات النمطية الأخرى. النظر في مقتطف الشفرة التالي:
A = rand(10,10) remotecall_fetch(()->sum(A), 2)
في هذه الحالة ، يجب تحديد sum في العملية عن بعد. لاحظ أن A هو متغير عمومي محدد في مساحة العمل المحلية. لا يحتوي العامل 2 على متغير باسم A في القسم Main . إرسال وظيفة الإغلاق () -> sum(A) للعامل 2 يؤدي Main.A تعريف Main.A 2. Main.A يستمر في الوجود على العامل 2 حتى بعد إرجاع استدعاء remotecall_fetch .

المكالمات عن بعد مع المراجع العالمية المدمجة (في الوحدة الرئيسية فقط) تدير المتغيرات العالمية على النحو التالي:
- يتم إنشاء روابط عمومية جديدة في محطات العمل الوجهة إذا تمت الإشارة إليها كجزء من مكالمة عن بعد.
- يتم الإعلان عن الثوابت العمومية ثوابت على العقد البعيدة أيضًا.
- يتم إعادة إرسال Globals إلى الموظف المستهدف فقط في سياق مكالمة عن بعد وفقط إذا تغيرت قيمتها. بالإضافة إلى ذلك ، لا يقوم النظام بمزامنة الارتباطات العالمية بين العقد. على سبيل المثال:
A = rand(10,10) remotecall_fetch(()->sum(A), 2)
يؤدي تنفيذ الجزء أعلاه إلى حقيقة أن Main.A على الموظف 2 لها قيمة مختلفة عن Main.A على الموظف 3 ، في حين أن قيمة Main.A على العقدة 1 هي صفر.
كما قد تفهم ، على الرغم من أنه يمكن جمع الذاكرة المرتبطة بالمتغيرات العامة عند إعادة تعيينها على الجهاز الرئيسي ، إلا أن مثل هذه الإجراءات لا تُتخذ للعاملين ، لأن الروابط لا تزال تعمل. واضح! يمكن استخدامها لإعادة تعيين متغيرات عمومية معينة يدويًا إلى nothing إذا لم تعد هناك حاجة إليها. سيؤدي ذلك إلى تحرير أي ذاكرة مرتبطة بها كجزء من دورة تجميع البيانات المهملة العادية. لذلك ، يجب أن تكون البرامج حذرة عند الوصول إلى المتغيرات العامة في المكالمات البعيدة. في الواقع ، كلما كان ذلك ممكنا ، من الأفضل تجنبها على الإطلاق. إذا كان يجب عليك الرجوع إلى المتغيرات العامة ، ففكر في استخدام كتل let لتوطين المتغيرات العامة. على سبيل المثال:
julia> A = rand(10,10); julia> remotecall_fetch(()->A, 2); julia> B = rand(10,10); julia> let B = B remotecall_fetch(()->B, 2) end; julia> @fetchfrom 2 InteractiveUtils.varinfo() name size summary ––––––––– ––––––––– –––––––––––––––––––––– A 800 bytes 10×10 Array{Float64,2} Base Module Core Module Main Module
من السهل معرفة أن المتغير العام A تعريفه على العامل 2 ، ولكن B مكتوب كمتغير محلي ، وبالتالي فإن الربط لـ B غير موجود على العامل 2.
حلقات موازية

لحسن الحظ ، لا تتطلب العديد من حسابات التزامن المفيدة حركة البيانات. مثال نموذجي هو محاكاة مونت كارلو ، حيث يمكن لعدة عمليات معالجة اختبارات المحاكاة المستقلة في وقت واحد. يمكننا استخدام @spawn لقلب العملات المعدنية إلى عمليتين. أولاً ، اكتب الوظيفة التالية في count_heads.jl :
function count_heads(n) c::Int = 0 for i = 1:n c += rand(Bool) end c end
تضيف الدالة count_heads ببساطة بتات عشوائية n. إليك كيفية إجراء بعض الاختبارات على جهازين وإضافة النتائج:
julia> @everywhere include_string(Main, $(read("count_heads.jl", String)), "count_heads.jl") julia> a = @spawn count_heads(100000000) Future(2, 1, 6, nothing) julia> b = @spawn count_heads(100000000) Future(3, 1, 7, nothing) julia> fetch(a)+fetch(b) 100001564
يوضح هذا المثال نمط برمجة متوازي قوي وشائع الاستخدام. يتم إجراء العديد من التكرار بشكل مستقل في العديد من العمليات ، ثم يتم دمج نتائجها باستخدام بعض الوظائف. تدعى عملية الاتحاد بالتقليل ، لأنها عادة ما تقلل من رتبة الموتر: يتم تقليل متجه الأرقام إلى رقم واحد ، أو يتم تقليل المصفوفة إلى صف واحد أو عمود ، إلخ. في التعليمات البرمجية ، يبدو هذا عادةً كما يلي: النموذج x = f(x, v [i]) ، حيث x هي البطارية ، f هي وظيفة التخفيض ، و v[i] هي العناصر التي يجب تقليلها.
من المستحسن أن تكون f مرتبطة ببعضها البعض حتى لا يهم ترتيب إجراء العمليات. يرجى ملاحظة أنه قد يتم تعميم count_heads لهذا القالب مع count_heads . استخدمنا بيانين spawn صريحين ، مما يحد من التزامن إلى عمليتين. للتشغيل على أي عدد من العمليات ، يمكننا استخدام متوازي للحلقة العاملة في الذاكرة الموزعة ، والتي يمكن كتابتها إلى جوليا باستخدام الموزعة ، على سبيل المثال:
nheads = @distributed (+) for i = 1:200000000 Int(rand(Bool)) end
( (+) ). . .
, for , . , , , . , , . , :
a = zeros(100000) @distributed for i = 1:100000 a[i] = i end
, . , . , Shared Arrays , , :
using SharedArrays a = SharedArray{Float64}(10) @distributed for i = 1:10 a[i] = i end
«» , :
a = randn(1000) @distributed (+) for i = 1:100000 f(a[rand(1:end)]) end
f , . , , . , Future , . Future , fetch , , @sync , @sync distributed for .
, (, , ). , , Julia pmap . , :
julia> M = Matrix{Float64}[rand(1000,1000) for i = 1:10]; julia> pmap(svdvals, M);
pmap , . , distributed for , , , . pmap , distributed . distributed for .
(Shared Arrays)

Shared Arrays . DArray , SharedArray . DArray , ; , SharedArray .
SharedArray — , , . Shared Array SharedArrays , . SharedArray ( ) , , . SharedArray , . , Array , SharedArray , sdata . AbstractArray sdata , sdata Array . :
SharedArray{T,N}(dims::NTuple; init=false, pids=Int[])
N - T dims , pids . , , pids ( , ).
init initfn(S :: SharedArray) , . , init , .
:
julia> using Distributed julia> addprocs(3) 3-element Array{Int64,1}: 2 3 4 julia> @everywhere using SharedArrays julia> S = SharedArray{Int,2}((3,4), init = S -> S[localindices(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 3 4 4 julia> S[3,2] = 7 7 julia> S 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 7 4 4
SharedArrays.localindices . , , :
julia> S = SharedArray{Int,2}((3,4), init = S -> S[indexpids(S):length(procs(S)):length(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 2 2 3 3 3 3 4 4 4 4
, , . على سبيل المثال:
@sync begin for p in procs(S) @async begin remotecall_wait(fill!, p, S, p) end end end
. pid , , ( S ), pid .
«»:
q[i,j,t+1] = q[i,j,t] + u[i,j,t]
, , , , , : q [i,j,t] , q[i,j,t+1] , , , q[i,j,t] , q[i,j,t+1] . . . , (irange, jrange) , :
julia> @everywhere function myrange(q::SharedArray) idx = indexpids(q) if idx == 0
:
julia> @everywhere function advection_chunk!(q, u, irange, jrange, trange) @show (irange, jrange, trange)
SharedArray
julia> @everywhere advection_shared_chunk!(q, u) = advection_chunk!(q, u, myrange(q)..., 1:size(q,3)-1)
, :
julia> advection_serial!(q, u) = advection_chunk!(q, u, 1:size(q,1), 1:size(q,2), 1:size(q,3)-1);
@distributed :
julia> function advection_parallel!(q, u) for t = 1:size(q,3)-1 @sync @distributed for j = 1:size(q,2) for i = 1:size(q,1) q[i,j,t+1]= q[i,j,t] + u[i,j,t] end end end q end;
, :
julia> function advection_shared!(q, u) @sync begin for p in procs(q) @async remotecall_wait(advection_shared_chunk!, p, q, u) end end q end;
SharedArray , ( julia -p 4 ):
julia> q = SharedArray{Float64,3}((500,500,500)); julia> u = SharedArray{Float64,3}((500,500,500));
JIT- @time :
julia> @time advection_serial!(q, u); (irange,jrange,trange) = (1:500,1:500,1:499) 830.220 milliseconds (216 allocations: 13820 bytes) julia> @time advection_parallel!(q, u); 2.495 seconds (3999 k allocations: 289 MB, 2.09% gc time) julia> @time advection_shared!(q,u); From worker 2: (irange,jrange,trange) = (1:500,1:125,1:499) From worker 4: (irange,jrange,trange) = (1:500,251:375,1:499) From worker 3: (irange,jrange,trange) = (1:500,126:250,1:499) From worker 5: (irange,jrange,trange) = (1:500,376:500,1:499) 238.119 milliseconds (2264 allocations: 169 KB)
advection_shared! , , .
, . , , .
, , , .
- Julia
, , , .
, , -. , حيث — . - , .. , .
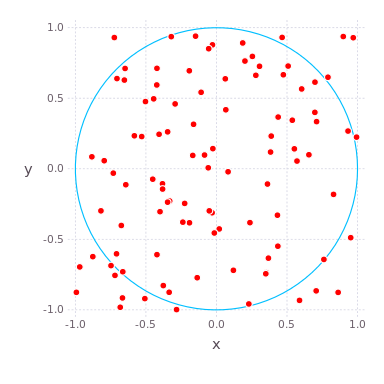
( , ) ( ) , , , . , , . compute_pi (N) , , .
function compute_pi(N::Int)
, , . : , , 25 .
Julia Pi.jl ( Sublime Text , ):
C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 julia> include("C:/Users/User/Desktop/Pi.jl")
using Distributed addprocs(4)
Jupyter
Pi.jl @everywhere function compute_pi(N::Int) n_landed_in_circle = 0
, :
julia> @time parallel_pi_computation(1000000000, ncores = 1) 6.818123 seconds (1.96 M allocations: 99.838 MiB, 0.42% gc time) 3.141562892 julia> @time parallel_pi_computation(1000000000, ncores = 1) 5.081638 seconds (1.12 k allocations: 62.953 KiB) 3.141657252 julia> @time parallel_pi_computation(1000000000, ncores = 2) 3.504871 seconds (1.84 k allocations: 109.382 KiB) 3.1415942599999997 julia> @time parallel_pi_computation(1000000000, ncores = 4) 3.093918 seconds (1.12 k allocations: 71.938 KiB) 3.1416889400000003 julia> pi ? = 3.1415926535897...
JIT - — . , Julia . , ( Multi-Threading, Atomic Operations, Channels Coroutines).
, , . MPI.jl MPI ,
DistributedArrays.jl .
GPU, :
- ( C) OpenCL.jl CUDAdrv.jl OpenCL CUDA.
- ( Julia) CUDAnative.jl CUDA .
- , , CuArrays.jl CLArrays.jl
- , ArrayFire.jl GPUArrays.jl
- -
- Kynseed
, , . !