ربط الأوتوماتيكية الخلوية مع الخوارزمية الجينية ومعرفة ما يحدث.
المقالة تحتوي على GIF (حركة المرور!) والصور المتناقضة. قد يكون الصرع نوبة صرع.قواعد لأتمتة الخلوية
إن أبسط الإضافات الخلوية هي إتمتة خلوية أحادية البعد (هناك أيضًا أبسط أبعاد صفرية - سنتحدث عنها أدناه). في نموذج تلقائي أحادي البعد ، لدينا صفيف أحادي البعد ، يمكن للخلايا (الخلايا) أن تأخذ واحدة من حالتين (1/0 ، صواب / خطأ ، أبيض / أسود ، حي / ميت). يتم تحديد الحالة التالية للخلية في المصفوفة حسب الحالة الحالية للخلية وحالة خليتين مجاورتين ، وفقًا لبعض القواعد.
المجموع موجود
23=8 مجموعات من حالات الخلايا وخليتين مجاورتين:

بعد ذلك ، لكل مجموعة من المجموعات ، نكتب حالة الخلية للتكرار التالي (للحالة التالية من الأوتوماتون):
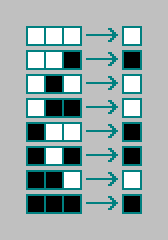
حصلت على قاعدة لآلية الخلوية. يتم ترميز قواعد الأوتوماتيكية الخلوية أحادية البعد بثمانية بتات ("رمز التنغستن"). المجموع موجود
28=256دولا الأوتوماتيكية الخلوية الابتدائية:
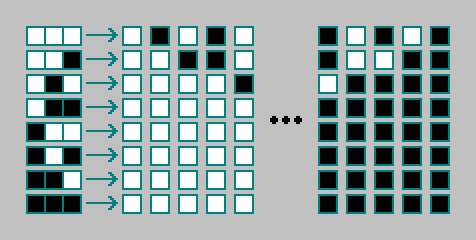
يمكن فرز 256 جهازًا يدويًا. لن نتطرق إليهم. نحن نحسب عدد القواعد الحالية لآلات الخلوية ثنائية الأبعاد.
يستخدم الإكمال التلقائي الخلوي ثنائي الأبعاد صفيف ثنائي الأبعاد. يوجد في كل خلية 8 جوار بالقرب من مور (يوجد أيضًا حي فون نيومان لا تؤخذ فيه الخلايا القطرية بعين الاعتبار. لن نأخذها بعين الاعتبار في المقال):

للراحة ، نكتب الخلايا في سطر (سنستخدم الترتيب المحدد لاحقًا في المقالة):
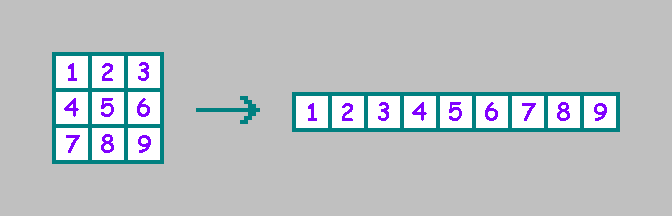
لأوتوماتون الخلوية ثنائي الأبعاد هناك
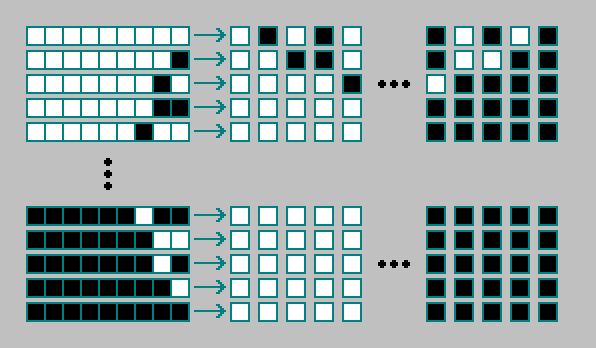
29=512 مجموعات من حالات الخلايا و 8 خلايا مجاورة:

يتم ترميز القاعدة الخاصة بأتمتة خلوية ثنائية الأبعاد بتردد 512 بت. المجموع موجود
2512 ثنائي الأبعاد الآلي الخلوية:
عدد:
2512 approx1.340781 times10154
المزيد من
الذرات في الكون المرئي (
1080 ).
يدويا لا يمكن فرز هذا العدد من الآلات. إذا نظرنا إلى آلية واحدة كل ثانية - أثناء وجود الكون ، لكنا تمكنا من إلقاء نظرة على كل شيء
approx4.35 times1017 آلات أوتوماتيكية.
لا يعمل التعداد البسيط ، ولكن بمساعدة خوارزمية جينية ، يمكننا أن نجد الآلي الذي يناسب معايير محددة سلفًا بشكل أفضل.
سنقوم البرنامج في جافا سكريبت. يتم إخفاء كل أجزاء الشفرة تحت المفسدين حتى لا تخلط بين القراء الذين ليسوا على دراية بلغات البرمجة.
ثنائي الأبعاد التلقائي الخلوية
نكتب التلقائي الخلوية ثنائي الأبعاد مع قاعدة عشوائية. سنخزن القاعدة في مصفوفة القاعدة ، وطول المدة التي يحددها = 512:
ملء مجموعة القاعدةvar rulesize=512; var rule=[]; for(var i=0;i<rulesize;i++) rule[i]=Math.round(Math.random());
بعد ذلك ، املأ الحالة الأولية للجهاز بمنزل عشوائي:
نحن نملأ الحالة الأولية للجهاز var sizex=89; var sizey=89; var size=2; var a=[]; for(var x=0;x<sizex;x++){ a[x]=[] for(var y=0;y<sizey;y++){ a[x][y]=Math.round(Math.random()); if(a[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } }
(هنا وبعد ذلك في المقالة ، مثل عرض وارتفاع الآلة ، يتم أخذ رقم عشوائي - ليس كبيرًا جدًا ولا صغير جدًا رقم 89)تبدو الوظيفة التي تحسب الحالة التالية للأوتوماتون كالتالي (لكي لا تتناثر ، فقد أزالت تهيئة اللوحة القماشية):
نحن نعتبر الحالة التالية للأوتوماتون function countpoints(){ var temp=[]; var xm, xp, ym, yp, q; for(var x=0;x<sizex;x++){ xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0; temp[x]=[]; for(var y=0;y<sizey;y++){ ym=y-1; if(ym==-1) ym=sizey-1; yp=y+1; if(yp==sizey) yp=0; q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q]; if(temp[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } } a=temp; }
تقوم المتغيرات xm و xp بتخزين إحداثيات X للجار على اليسار والجار على اليمين (x ناقص و x plus). تقوم المتغيرات ym و yp بتخزين إحداثيات Y المقابلة.
هنا:
يتم تدوير مجال الآلة في الخبز xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0;
نحدد شروط الحدود الدورية (مجال الأوتوماتون هو سطح التوروس).
التالي:
... كذلك q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q];
بالترتيب أعلاه ، اكتب محتويات الخلايا في سلسلة. نحن نترجم السلسلة إلى رقم عشري. بالنسبة لهذه المجموعة ، نجد في صفيف القاعدة الحالة التي يجب أن تأخذها الخلية بإحداثي x و y.
الخيار الأمثل q=a[xm][ym]; q=(q<<1)+a[x][ym]; q=(q<<1)+a[xp][ym]; q=(q<<1)+a[xm][y]; q=(q<<1)+a[x][y]; q=(q<<1)+a[xp][y]; q=(q<<1)+a[xm][yp]; q=(q<<1)+a[x][yp]; q=(q<<1)+a[xp][yp]; temp[x][y]=rule[q];
بعد كل التكرارات ، استبدل الحالة السابقة للأوتوماتون بحالة جديدة:
استبدل الحالة السابقة بحالة جديدة نرسم آلية باستخدام وظيفة setInterval:
setInterval timerId = setInterval(function() { countpoints(); }, 1);
تشغيل في المتصفحأوصي ببدء تشغيل الجهاز بقواعد عشوائية 10-20 مرة قبل متابعة قراءة المقال.
يمكننا تشغيل الجهاز لفترة طويلة جدا مع قواعد عشوائية مختلفة. الصورة التي نحصل عليها لن تختلف عن الصورة على شاشة التلفزيون في حالة عدم وجود إشارة:

بعد ذلك ، دعنا ننتقل إلى إعداد "تلفزيوننا" باستخدام الخوارزمية الجينية.
الخوارزمية الجينية
حجم السكان الأولي هو 200 آلة (أفراد). بالنسبة للقواعد ، بدلاً من مجموعة أحادية البعد من القواعد ، سنستخدم مجموعة ثنائية الأبعاد من السكان. المؤشر الأول (ن) هو عدد الأفراد في السكان.
خلق السكان var PopulationSize=200; var rulesize=512; var population=[]; var fitness=[]; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
يحتوي صفيف اللياقة البدنية على معاملات اللياقة البدنية لكل فرد. يتم ملء هذا الصفيف في عملية الاختيار. بعد الاختيار ، نبدأ العملية التطورية.
عملية تطورية
من سكاننا نأخذ نصف الأفراد الأكثر تكيفًا (وفقًا لمعامل اللياقة). تم تدمير النصف المتبقي. بعد ذلك ، نأخذ شخصين على قيد الحياة ونعبرهما.

للعبور ، حدد موقعًا عشوائيًا في الأنماط الجينية لأسلاف. قبل هذا الموقف ، نأخذ جينات من سلف واحد ، وبعد هذا الموقف - من آخر. نضع الجينات المحددة في التركيب الوراثي على سليل واحد. الجينات المتبقية هي لآخر. نحن نضع اثنين من الأسلاف ونسلين في عدد سكان جديد. في الوقت نفسه ، يشارك كل فرد في المعبر مرة واحدة.
الطفرات. مع وجود احتمال بنسبة 5٪ ، يتحول جين واحد تم اختياره عشوائيًا (ينقلب) في كل فرد. إذا قمت بزيادة احتمال حدوث طفرات ، سيكون هناك المزيد من الطفرات الناجحة ، ولكن في نفس الوقت ، قد لا يكون للطفرات الناجحة الوقت لترك ذرية ناجحة قبل أن يتغير مرة أخرى دون جدوى. سوف نعود إلى هذه المشكلة لاحقًا.
وظيفة تتطور () ؛ function evolute(){ var sizehalf=PopulationSize/2; var sizequarter=sizehalf/2; var arrayt=[]; for(var n=0; n<PopulationSize; n++) arrayt[n]=[population[n], fitness[n]]; arrayt.sort(sortf); arrayt.length=sizehalf; population=[]; fitness=[]; for(var i=0; i<sizequarter; i++){ var i0=i*4; var i1=i*4+1; var i2=i*4+2; var i3=i*4+3; var removed1=Math.floor(Math.random()*(arrayt.length)); var parent1f = arrayt.splice(removed1,1); var parent1=parent1f[0][0]; var removed2=Math.floor(Math.random()*(arrayt.length)); var parent2f = arrayt.splice(removed2,1); var parent2=parent2f[0][0]; var child1=[]; var child2=[]; var qen=Math.floor(Math.random()*rulesize); var temp0=parent1; var temp1=parent2; var temp2=temp0.splice(qen,rulesize); var temp3=temp1.splice(qen,rulesize); var parent1=temp0.concat(temp2); var parent2=temp1.concat(temp3); var child1=temp1.concat(temp2); var child2=temp0.concat(temp3); population[i0]=parent1; population[i1]=parent2; population[i2]=child1; population[i3]=child2; fitness[i0]=0; fitness[i1]=0; fitness[i2]=0; fitness[i3]=0; } var mutation=document.getElementById("mutatepercent").value*1; var m=100/mutation; var m2=0;
الانتقاء الطبيعي
قبل البدء في العملية التطورية ، يجب أن يتم الاختيار. يمكن أن يكون الاختيار طبيعيًا ومصطنعًا. يتم اختيار الاصطناعي يدويا - حول هذا الموضوع في وقت لاحق قليلا. للانتقاء الطبيعي ، سنضع بعض المعايير ونختار الآلات التي تتوافق بشكل أفضل مع المعايير المحددة.
ما هي المعايير التي يمكن تحديدها مقدما؟ خذ أسهل واحد. لدينا "TV" وامض أكثر من اللازم. نحن ننقذ حالتين من الأوتوماتون الخلوي - في 99 وفي 100 تكرار. حساب عدد الخلايا التي لم تتغير. سيتم استخدام الرقم الناتج باعتباره معامل اللياقة. من الواضح ، معيار واحد لا يكفي بالنسبة لنا. من السهل تحديد الأوتوماتون الذي يلبي المعيار المحدد: الأوتوماتون [0،0،0، ...، 0] والأوتوماتون [1،1،1، ...، 1]. في التكرار الأول ، تمتلئ هاتان الأوتوماتيتان بالأصفار أو تلك وتتوقفان عن تغيير حالتهما. نحدد المعيار الثاني: لا يتجاوز الفرق بين عدد 0 و 1 (خلايا) في الجهاز 100 (يتم أخذ الرقم "من الجرافة").
array1 - حالة الأوتوماتون في التكرار 99. array2 - في التكرار المائة:
نحن نعتبر ذلك function countfitness(array1, array2){ var sum=0; var a0=0; var a1=0; for(var x=0;x<sizex;x++){ for(var y=0;y<sizey;y++){ if(array1[x][y]==array2[x][y]) sum++; if(array1[x][y]==0){ a0++; }else{ a1++; } } } if(Math.abs(a0-a1)<100) return sum; return 0; }
نبدأ. تم العثور على الحل الأمثل في دورة التطور 421. على الرسم البياني يمكنك رؤية التقدم:
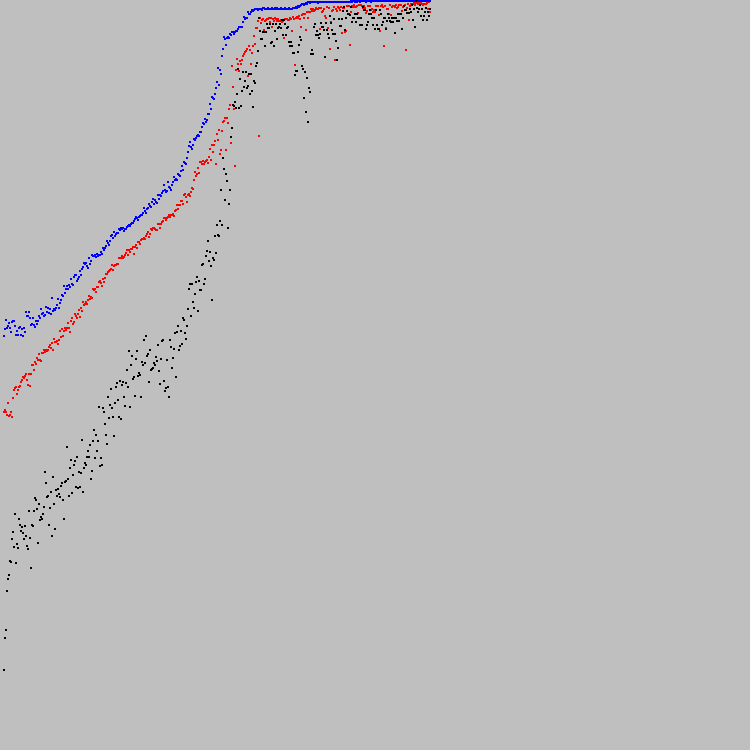
يتم قياس الرسم البياني على طول المحور ص. والنقطة الأدنى هي 0 ، وأعلى نقطة هي 7921. ومن الواضح أن 7921 هو الحل الأمثل (جميع الخلايا في جهاز 89x89 تلبي المعيار المحدد). بعد 100 تكرار ، لا توجد خلية تغير حالتها.
النقاط الزرقاء على الرسم البياني هي أفضل فرد في السكان. ريدز هي الأسوأ (فقط الأفراد الذين يستوفون المعيار الثاني يؤخذون في الاعتبار). النقاط السوداء - متوسط معامل اللياقة لجميع السكان (مع مراعاة الأفراد الذين لا يستوفون المعيار الثاني). المعيار الثاني (التوازن بين الأبيض والأسود) صعب للغاية. لا تلبي بعض الأوتماتة المعيار الثاني حتى بعد 421 دورة تطور. لذلك ، النقاط السوداء هي أقل من الأحمر.
مجموعة الجينات من السكان (الأفراد على طول المحور Y ، الجينات على طول المحور X):

دعونا نرى القناة التي اشتعلت فيها "تلفزيوننا":

الحل الموجود ليس هو الحل الأمثل الوحيد. إذا أعدنا تشغيل التطور (باستخدام أنماط وراثية أولية عشوائية) ، فسنجد الحلول المثلى الأخرى. واحد منهم:

تغيير معايير الاختيار.
سننظر في عدد الخلايا التي يظهر لها نمط في جوار Moore of order 2. لنأخذ أبسط نمط:
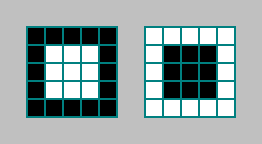
هذا المعيار مثير للاهتمام حيث أننا نتحقق من 25 خلية ، بينما يحسب الأوتوماتون حالة الخلية بناءً على حالات 9 خلايا.
المعيار صارم جدا. إذا أخذنا آليًا عشوائيًا ، فبعد 100 تكرار يبدو كما يلي:

لا توجد خلية واحدة في مثل هذا الإيفون تفي بالمعيار المحدد. لذلك ، نخفف المعيار قليلاً:
- لنرتكب خطأً واحدًا في النموذج.
- لن نبحث عن النموذج في التكرار الأخير ، ولكن في التكرارات الخمسين الأخيرة.
تتم إزالة المعيار الثاني (التوازن بين الأبيض والأسود).
نبدأ. الجدول الزمني:
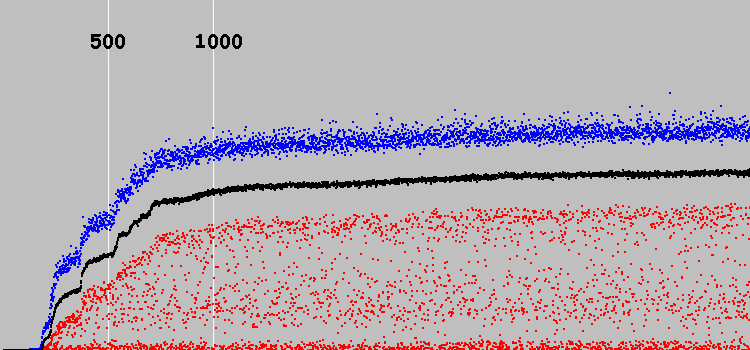
محور ذ تعسفي. (في الجهاز السابق ، الحل الأمثل هو 7921. في هذا الجهاز ، حوالي 30.)
المحور السيني - 3569 دورة تطور. يمثل خطان رأسيان أبيضان 500 و 1000 دورة من التطور.
النقاط الزرقاء - أفضل فرد في السكان ، أحمر - الأسوأ ، أسود - متوسط النسبة لجميع السكان.
تم العثور على الحل في أول 500 دورة من التطور. ال 500 دورة المقبلة ، والحل يتحسن. ثم يتوقف النظام عمليا عن التطور.
في الصور الثلاث أدناه: 500 دورة ، 1000 دورة و 3569 دورة تطور:



تجمع الجينات (3569):

في الديناميات:

في الصورة أدناه ، يمكنك رؤية كيفية تشكيل مذبذب (طائرة شراعية) في هذا الجهاز:

يمكننا بدء تشغيل الجهاز بالحالة الأولية التي يتم فيها ملء خلية واحدة. بعد ذلك ، قم بإصلاح جميع مجموعات الخلايا الموجودة في التكرارات التالية من الأوتوماتون. مجموعة من الجينات (النمط الوراثي لآلية) هي مجموعة من جميع المجموعات الممكنة. بعد عزل المجموعات التي تحدث فقط ، يمكننا بسهولة ملاحظة جميع الجينات التي تشارك في تكوين المذبذب. الأشرطة الرمادية هي جينات لا تشارك في تكوين المذبذب:

الطفرات في هذه الجينات لا تتجذر بسبب حقيقة أنها تعطل تشكيل النمط.
في آلة لدينا ، يتم تشكيل نمط (مربع) حول خلية سوداء فقط. دعونا نحاول بدء العملية التطورية مع المعيار الثاني: الفرق بين عدد الخلايا البيضاء والسوداء لا يتجاوز 400.
نبدأ 3569 دورات التطور. الجدول الزمني:
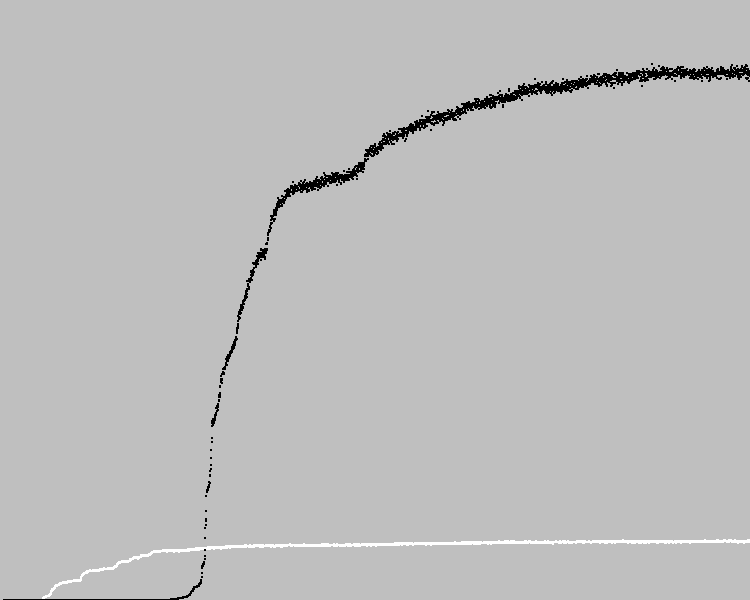
النقاط السوداء على الرسم البياني هي متوسط معامل اللياقة في عدد السكان. النقاط البيضاء - متوسط معامل اللياقة للجهاز السابق. العثور على حل مع خطأ واحد في النمط.
تجمع الجينات:

100 التكرار الأول:

(100) التكرار الأخير:

قليلا ليس النتيجة التي توقعناها. هناك المربعات السوداء والأبيض - لا. تشديد المعيار الثاني: الفرق بين عدد الخلايا البيضاء والسوداء لا يتجاوز 100.
نبدأ 14865 دورات التطور.
الرسم البياني يقارن متوسط معاملات اللياقة البدنية للسكان. النقاط الزرقاء هي مدفع رشاش. الأبيض والأسود هي الآلات السابقة.

تتطور الأوتوماتون بقوة بحيث يبدو أنها لا تتطور على الإطلاق. يتم قياس الرسم البياني الثاني على طول المحور ص.خطان أبيضان - 500 و 1000 دورة.
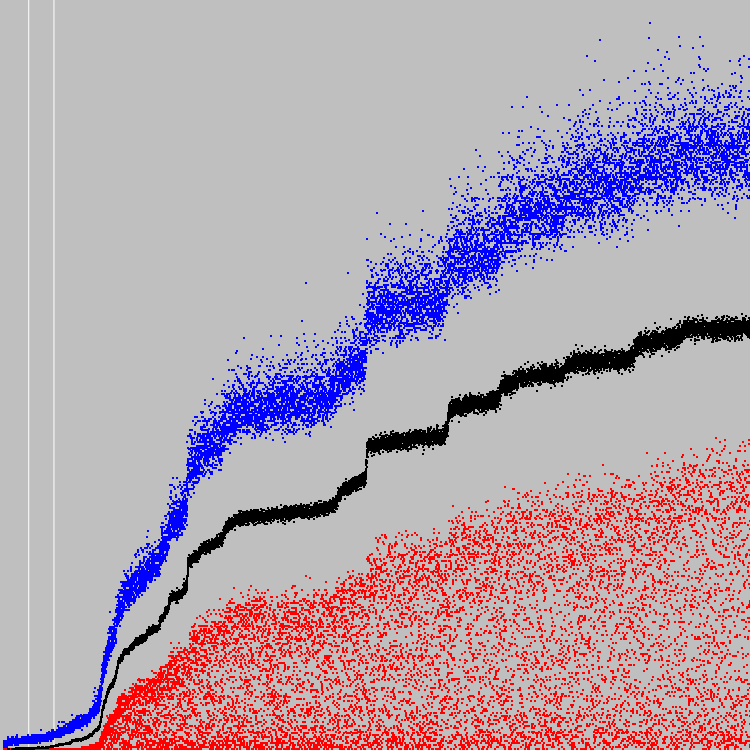
في أفضل فرد ، في المتوسط ، 6 خلايا تتوافق مع معيار معين.
دعونا نلقي نظرة على آلة عشوائية من السكان.
50 تكرار:

آخر (50) تكرار:

لم يتم العثور على نتيجة مقبولة. المعيار الثاني يعقد عملية البحث ، لذلك سنرفضه (لن نستخدمه لاحقًا في المقالة). دعنا نترك هذا النمط وابحث عن بعض الأنماط الأخرى.
نمط:

نبدأ. 3000 دورة من التطور. الجدول الزمني:
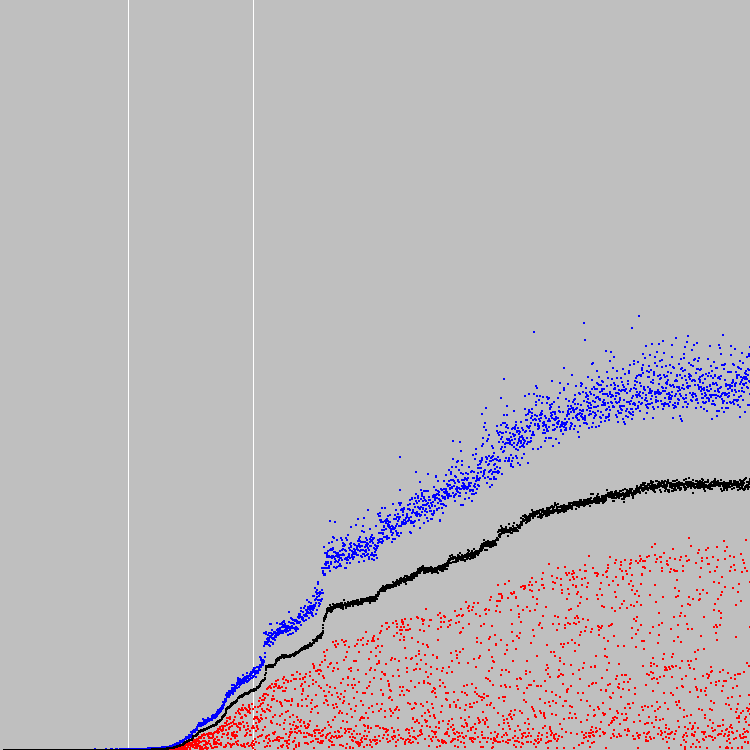
تجمع الجينات:

في الديناميات (100 تكرار):

(100) التكرار الأخير:

نمط:

في الأجهزة السابقة ، سمحنا لارتكاب خطأ واحد في النمط. هذه المرة ، دعونا نبحث عن النمط الدقيق.
نبدأ 4549 دورات التطور. الجدول الزمني:
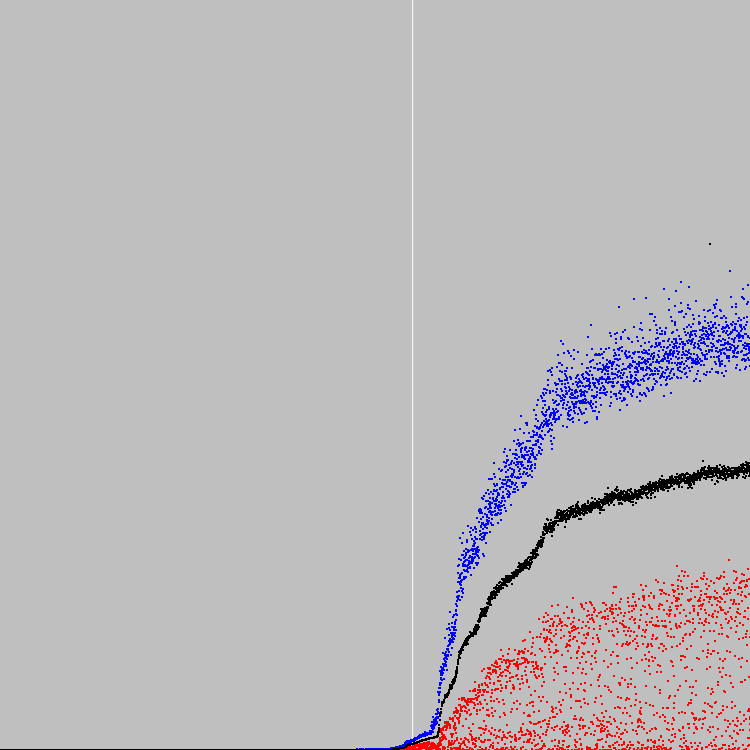
الخط العمودي الأبيض - 2500 دورة من التطور. في هذه المرحلة (قبل ذلك بقليل) ، بدأت اللياقة البدنية للسكان تنمو بسرعة. أنقذ السكان للنظر في حل مؤقت. تبين أن الحل الوسيط أكثر إثارة للاهتمام من الحل في دورة التطور 4549.
الحل الموجود في دورة التطور 4549:

هناك 100 تكرار على GIF. بعد عدد معين من التكرارات (حوالي 500-2000) ، يتم ترتيب حالة الأوتوماتون بالكامل تقريبًا (يتم اختيار ارتفاع وعرض الأوتوماتون خصيصًا بالأرقام الفردية بحيث لا يمكن طلب الإكمال التلقائي بالكامل):

يتخذ الإكمال التلقائي ذي الأحجام المتساوية من الجوانب ، بعد عدد معين من التكرارات ، حالة مرتبة بالكامل. 90 × 90 تلقائيًا ، حوالي 1200 تكرار:

حل وسيط (موجود في دورة التطور 2500):

يعرف هذا الإضافات الآلية أيضًا كيفية معالجة حالة فوضى مبدئية معينة إلى حالة محددة محددة (الحالة النهائية المطلوبة هي تحول النمط على طول المحور X إلى خلايا خلايا المذبذب اليسرى).
تم فرز الجهاز 16 × 16 في حوالي 100 تكرار:

32 × 32 - حوالي 1000 تكرار:

64 × 64 - حوالي 6000 تكرار:

90 × 90 - حوالي 370000 تكرار:

11 × 11 (الأبعاد الفردية لحقل التشغيل التلقائي) - حوالي 178700 تكرار:

لم بندقية الهجوم 13x13 لم تأمر في كمية مقبولة من الوقت.
في الصورة أدناه ، الجهاز على الحقل 256 × 256 في التكرار 100000:

أوصي بالنظر إلى هذا الإضافات التلقائية في ديناميكيات حقل كبير - من المثير للاهتمام ملاحظة عملية التنظيم الذاتي للفوضى في هذا الإوتون:
تشغيل في متصفحتجمع الجينات من السكان المتوسطة:

تسمح لك إعادة تشغيل العملية التطورية بالعثور على حلول أخرى. واحد منهم:


نمط آخر:
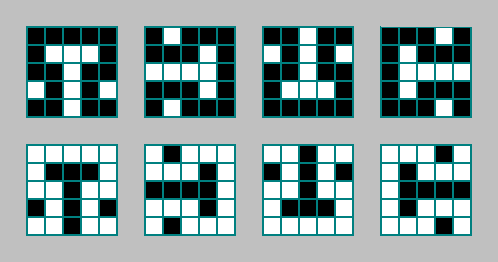
عند البحث عن نمط ، دعنا نخطئ مرة أخرى (بدون أخطاء ، لن يتطور النظام ذي النمط المحدد).
نبدأ. 5788 دورات التطور. الجدول الزمني:
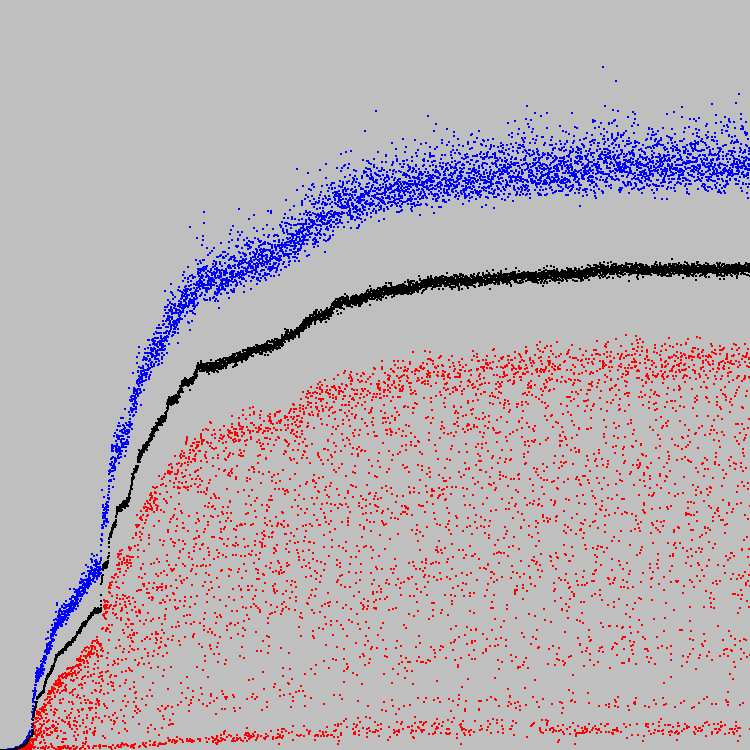
المقياس تعسفي.
تجمع الجينات:

في الديناميات:

حالة الترتيب التلقائي (تحول النمط لأعلى على طول المحور ص + عدة خلايا مذبذب):

إنه أكثر إثارة للاهتمام أن نلاحظ ليس الجهاز نفسه ، ولكن المسوخ الذي يظهر في هذه الفئة من السكان:
على Gif ، يكون الجهاز 256 × 256. 200 التكرار. يمكن
الاطلاع على التكرارات المتبقية
في المتصفح .
يمكن للمرء أن ينتهي مع الانتقاء الطبيعي والانتقال إلى مصطنع ، لكنني أريد أن أوضح كم
2512 عدد ضخم. من بين هذا العدد من الأوتوماتة ، يمكننا العثور على إنسان آلي يرسم أي نمط معين (مع بعض الدقة للأنماط الأكثر تعقيدًا).
النمط التالي:

في التجارب السابقة ، قمنا بحساب مجموع الخلايا التي يتم تشكيل النموذج حولها (إذا حدث خطأ واحد ، فأضف 1 إلى المجموع ، وإذا لم يكن هناك أخطاء ، أضف 2). تم استخدام المبلغ الناتج كعامل لياقة للخوارزمية الجينية.
بالنسبة لنمط أكثر تعقيدًا ، لا تعمل هذه الطريقة. إن الأوتوماتون الذي يتطابق فيه عدد أصغر من الخلايا مع معيار معين (عدد الخلايا المطابقة لنمط في المنطقة المجاورة للخلية) سيخسر في كل مرة لإكمال تلقائي يتطابق فيه عدد أكبر من الخلايا مع معيار معيّن بدقة أكبر. كما في المثال مع المربعات أعلاه:

بالنسبة للنمط المرغوب ، عند التكرار رقم 100 لكل آلية في المجتمع ، محاطة بكل خلية ، سننظر في عدد الخلايا المطابقة للنمط. سنتخذ فقط أفضل نتيجة لكل جهاز. سيتم استخدام عدد الخلايا المطابقة للنمط كعامل لياقة. يتكون النموذج من 7x17 = 119 خلية. سيتم اعتبار هذا الرقم الحل الأمثل. سمحت لنا 6000 دورة من التطور بالعثور على نموذج آلي يرسم نمطًا به 5 أخطاء (تتزامن 114 خلية مع النمط).
الرسم البياني على نطاق التعسفي:
زيادة في نسبة الطفرات لم تضعف من اللياقة البدنية للسكان.
هناك العديد من الطفرات في مجموعة الجينات من السكان:

التشغيل التلقائي العشوائي من مجتمع في الديناميات:

أفضل آلة في التكرار المائة:

بحثت وجدت أنماط:

بعد أن لعبت مع معايير الاختيار ، وحجم مجال التشغيل الآلي والنسبة المئوية للطفرات ، اتضح أن تحسين السكان والعثور على آلية تجعل 3 أخطاء فقط في النموذج.
تجمع الجينات:

الجهاز في التكرار 100:

بحثت وجدت أنماط:

2 أخطاءفي عملية كتابة المقال ، استمر تطور النظام. لإجراء بحث أكثر دقة ، تمت زيادة حجم حقل الجهاز إلى 513 × 513. تم العثور على إنسان آلي يصنع خطأين فقط في النموذج:

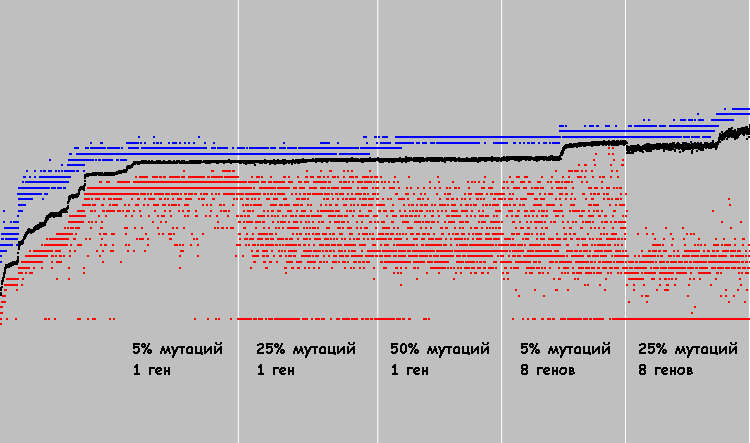
في أربعة رسوم بيانية ، يمكنك أن ترى كيف يتطور النظام مع احتمالات طفرة مختلفة (طفرة جين واحد):
النقاط الحمراء هي متوسط معامل اللياقة لدى السكان. النقاط السوداء هي معامل اللياقة البدنية لكل فرد. 3000 دورة تطور لكل نظام.
تجمعات الجينات من السكان (بنفس الترتيب):




Automata في التكرار المائة:




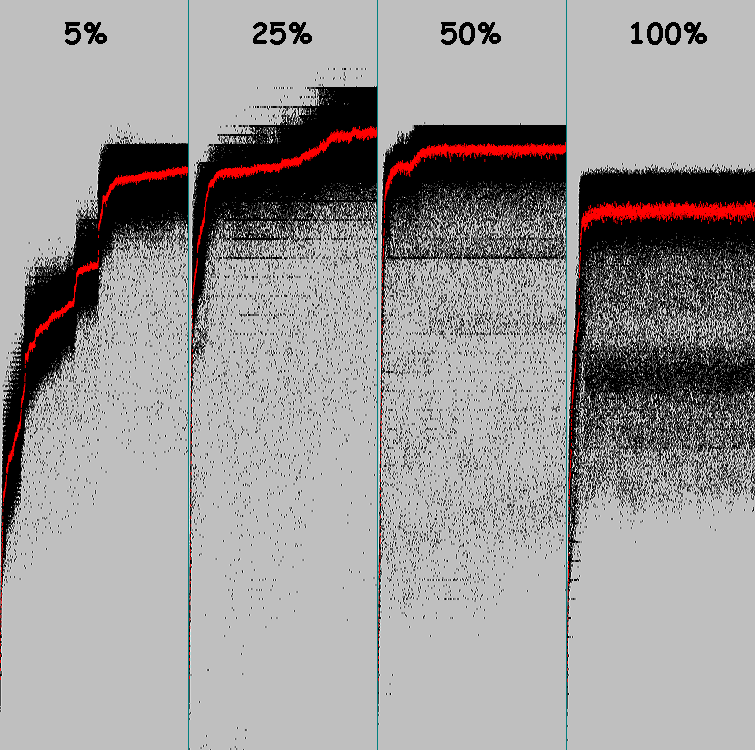
دعونا نفعل تجربة أخرى. النمط هو نفسه. تمتلئ الأنماط الجينية الأولية مع الجينات العشوائية. احتمال حدوث طفرات 5٪. من 1 إلى 8 جينات متحولة (يتم أخذ عدد عشوائي من الجينات المتحولة لكل فرد). 100 دورة من التطور.

الرسم البياني هو خريطة الحرارة. حجم النقطة على المخطط هو 5 بكسل. الأصل هو الزاوية اليسرى العليا.
على المحور ص (من 0 إلى 100) - دورات التطور. على المحور X (من 0 إلى 119) - عدد الخلايا المتزامنة مع النموذج (لكل فرد في المجتمع نأخذ أفضل نتيجة). سطوع النقطة هي عدد الأفراد الذين لديهم النتيجة المحددة (إحداثي X).
قم بتشغيل الخوارزمية الجينية 4 مرات بنفس المعلمات (100 دورة ، 5٪ طفرات ، ما يصل إلى 8 جينات متحولة). على الرسم البياني ، يبدأ كل 5:

يبدأ الـ 5 التالية: 25٪ طفرات ، حتى 8 جينات متحولة:

العينة صغيرة ، ولكن يمكننا استخلاص استنتاجات حول فعالية زيادة نسبة الطفرات.
بعد ذلك ، سأظهر عدم كفاءة طريقة العبور المستخدمة في المقالة.
الطريقة المستخدمة سابقا:

بدلاً من تقسيم النمط الوراثي إلى جزأين ، سيرث المتحدرون جينات أجداد عشوائية:
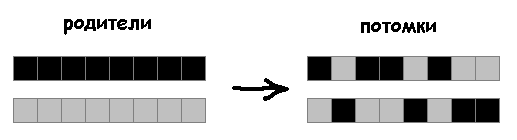
طفرات 5 ٪:

25٪:

التالي سوف نستخدم هذه الطريقة من الصلبان.
على هذا مع الانتهاء من الانتقاء الطبيعي. إذا كان لدى شخص ما أفكار مثيرة للاهتمام حول معايير الانتقاء الطبيعي - يرجى التعبير عنها في التعليقات.
لاختيار اصطناعي سوف نستخدم
أوتوماتا الخلوية من الدرجة الثانية .
النظام الآلي الخلوية من الدرجة الثانية
خذ بعين الاعتبار التشغيل التلقائي الخلوي الصفري من الدرجة الأولى (جميع أوتوماتات الخلوية التي اعتبرناها أعلاه من الدرجة الأولى). يتكون الإكمال التلقائي الخلوي ذو الأبعاد الصفرية من خلية واحدة. يمكن أن تكون الخلية في واحدة من حالتين. يتم تحديد الحالة التالية للخلية (t) حسب الحالة الحالية للخلية (t-1). في المجموع ، هناك 4 أوتوماتات خلوية ذات أبعاد صفرية (من بينها مذبذب واحد):
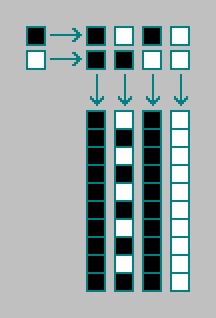
في التشغيل التلقائي الخلوي من الدرجة الثانية ، يتم تحديد الحالة التالية للخلية (t) حسب الحالة الحالية (t-1) والحالة السابقة للخلية (t-2). في المجموع ، هناك 4 مجموعات من دولتين من الخلايا.
24=16دولارً - عدد الأوتوماتة الخلوية ذات الأبعاد الصفرية من الدرجة الثانية:

مثل هذه الأوتوماتيكية الخلوية تظهر مؤشرات التذبذب أكثر تعقيدًا.
28=256دولا الآلي الخلوية من الدرجة الثالثة:
 216=65536
216=65536 لا يمكن إظهار الأوتوماتة الخلوية من الدرجة الرابعة في صورة واحدة.
البحث التلقائي للخلية ن -الترتيب مع فترة التذبذب تساوي ن - المهمة غير تافهة ومثيرة للاهتمام للغاية. هذا الموضوع يستحق مقالة منفصلة.في الأوتوماتيكية الخلوية أحادية البعد ثنائية الأبعاد ، يتم تحديد الحالة التالية للخلية بواسطة الحالة الحالية لثلاث خلايا والحالة السابقة لخلية واحدة:
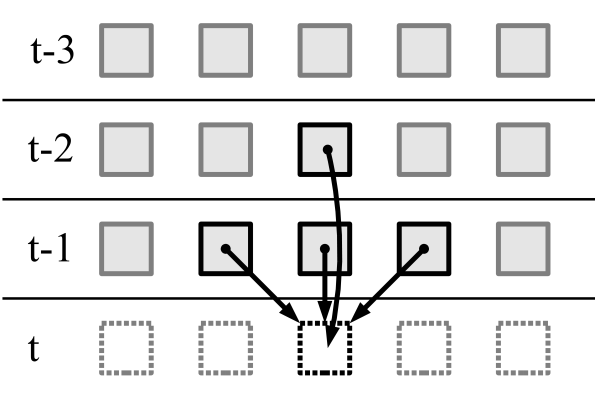
هناك
216=65536 أبسط الأبعاد الخلوية من الدرجة الثانية.
كود:
var rule=[]; for(var i=0;i<16;i++) rule[i]=Math.round(Math.random()); var a=[]; var b=[]; var temp; for(var x=0;x<sizex;x++){ a[x]=0; b[x]=0; } b[63]=1; var xm, xp, q; for(var y=2;y<sizey;y++){ temp=[]; for(var x=0;x<sizex;x++){ xm=x-1; if(xm<0) xm=sizex+xm; xp=x+1; if(xp>=sizex) xp=xp-sizex; q=b[xm]; q=(q<<1)+b[x]; q=(q<<1)+b[xp]; q=(q<<1)+a[x]; temp[x]=rule[q]; if(temp[x]) context.fillRect(x*size, y*size, size, size); } a=b; b=temp; }
 0101101110011110:
0101101110011110: 0110000110010010:
0110000110010010: 0110011010010110:
0110011010010110: 1110011010010110:
1110011010010110: 0110111010000101:
0110111010000101: 1111101001110110:
1111101001110110: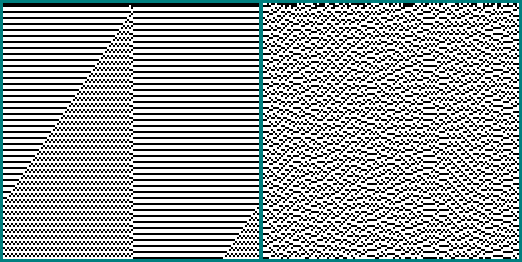 1001010001100000:
1001010001100000: الجهاز نفسه هو 256x256:
الجهاز نفسه هو 256x256: 512x512
512x512 يمكن العثور على الأجهزة الأخرى هنا:الجهاز الخلوي ثنائي الترتيب ثنائي الأبعاد.إنسان الخلوية الخلوية أحادية البعد من الدرجة الثالثة.يمكن العثور على الأوتوماتة الخلوية أحادية البعد من الدرجة الثانية في كتاب Wolfram's A New Kind of Science.
يمكن العثور على الأجهزة الأخرى هنا:الجهاز الخلوي ثنائي الترتيب ثنائي الأبعاد.إنسان الخلوية الخلوية أحادية البعد من الدرجة الثالثة.يمكن العثور على الأوتوماتة الخلوية أحادية البعد من الدرجة الثانية في كتاب Wolfram's A New Kind of Science.اختيار مصطنع
مثل الأوتوماتون الخلوي أحادي البعد من الدرجة الثانية ، في الأوتوماتون الخلوي ثنائي الأبعاد من الدرجة الثانية ، سنستخدم خلية إضافية من الحالة السابقة (t-2) للأوتوماتون.للراحة ، نضع هذه الخلية في بداية السطر الثنائي: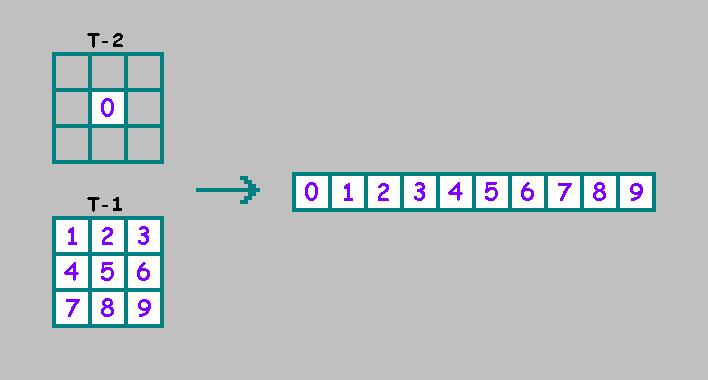 تكمن الراحة في حقيقة أنه عندما يتزامن النصف الأول والثاني من النمط الوراثي ، يمكن اعتبار الأوتوماتون كآلية ذاتية من الدرجة الأولى:
تكمن الراحة في حقيقة أنه عندما يتزامن النصف الأول والثاني من النمط الوراثي ، يمكن اعتبار الأوتوماتون كآلية ذاتية من الدرجة الأولى: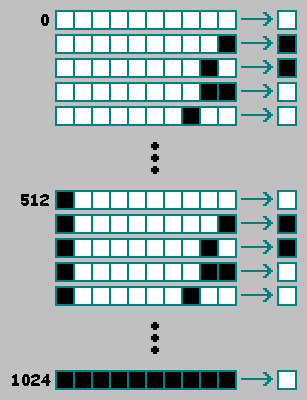 بإضافة خلية واحدة ، قمنا بزيادة عدد الأوتوماتا الموجودة في2 512 مرة.2 512 × 2 512 = 2 1024 - عدد الأوتوماتا ثنائية الأبعاد الموجودة من الدرجة الثانية. للانتقاء الطبيعي ، حددنا بعض المعايير وقارنا الأوتوماتة بهذا المعيار. في عملية الاختيار الاصطناعي ، نختار الآلات يدويًا باستخدام مبدأ غير واضح: "هذا الجهاز مثير للاهتمام ، لكن هذا ليس جيدًا للغاية." لا يسمح لك هذا المبدأ باختيار أفضل آلة بين الأجهزة العشوائية:هناك عدة طرق لحل هذه المشكلة. أقترح النظر في أربع طرق.
بإضافة خلية واحدة ، قمنا بزيادة عدد الأوتوماتا الموجودة في2 512 مرة.2 512 × 2 512 = 2 1024 - عدد الأوتوماتا ثنائية الأبعاد الموجودة من الدرجة الثانية. للانتقاء الطبيعي ، حددنا بعض المعايير وقارنا الأوتوماتة بهذا المعيار. في عملية الاختيار الاصطناعي ، نختار الآلات يدويًا باستخدام مبدأ غير واضح: "هذا الجهاز مثير للاهتمام ، لكن هذا ليس جيدًا للغاية." لا يسمح لك هذا المبدأ باختيار أفضل آلة بين الأجهزة العشوائية:هناك عدة طرق لحل هذه المشكلة. أقترح النظر في أربع طرق.





1. في الحالة الأولية للجهاز ، يتم ملء خلية واحدة
طريقة واحدة هي مراقبة تطور الأوتوماتيكية الخلوية ، في الحالة الأولية التي يتم فيها ملء خلية واحدة.نحن نملأ السكان الأولي مع آلات عشوائية. العديد من الآلات من السكان الأولي (30 تكرار لكل منها):

 هناك عدد صغير من الأوتوماتا التي تظهر سلوكًا أقل فوضوية في السكان. سنختارها للعبور:
هناك عدد صغير من الأوتوماتا التي تظهر سلوكًا أقل فوضوية في السكان. سنختارها للعبور:




 20 آلة عشوائية من المجموعة الأولية (حالة الآلات في التكرار الثلاثين):
20 آلة عشوائية من المجموعة الأولية (حالة الآلات في التكرار الثلاثين): بعد ثلاث دورات من التطور:
بعد ثلاث دورات من التطور: بعد ثماني دورات من التطور: كانت
بعد ثماني دورات من التطور: كانت ثماني دورات من التطور كافية لملء كل السكان بآلة مع سمة معينة (آلة ترسم مثلثات) .
ثماني دورات من التطور كافية لملء كل السكان بآلة مع سمة معينة (آلة ترسم مثلثات) .2. يتم ملء النمط الوراثي جزئيا
في حالة انتهاك نسبة الوحدات والأصفار في النمط الوراثي ، يتم انتهاك نسبة الوحدات والأصفار في النمط الظاهري.في النمط الوراثي (القاعدة) من الأوتوماتون ، يتم تسجيل شروط الخلية التالية لجميع التوليفات الممكنة للخلية والخلايا المجاورة. إذا كان هناك المزيد من الأصفار (أو تلك) في التركيب الوراثي ، فإن الأصفار (أو تلك) تتراكم في الحالات التالية للأوتوماتون. من المثير للاهتمام أن ننظر إلى العلاقة بين نسبة الأصفار والأصفار في التركيب الوراثي ونسبة الأصفار والأصفار في النمط الظاهري.بناء الرسم البياني.خلق عدد سكانها 200 آلة. نحن نملأ الأنماط الجينية بالأصفار (1024 جينًا في التركيب الوراثي لآلية تلقائية من الدرجة الثانية ثنائية الأبعاد). إضافين الجينات ملء وحدة. لأول السكانن = 0 ، للسكان 513ن = 512 .
على طول المحور x هو عدد السكان. على طول المحورص علامة (مع النقاط البيضاء) نسبة تلك والأصفار في تجمع الجينات من السكان. حصلناعلى مجموعة كبيرة من القطعالزائدة:بالنسبة لكل آلية تلقائية (بحجم حقل 89x89) ، فإننا نعتبر 100 تكرار. في التكرار المائة ، نحسب عدد الأصفار والأصفار في الحالة (النمط الظاهري) لكل إنسان آلي. نحتفل على الرسم البياني نسبة الوحدات والأصفار (إجمالي عدد جميع الوحدات مقسومًا على العدد الإجمالي لجميع الأصفار). حصلنا على منحنى:بدلاً من النسبة الإجمالية للأصفار والأصفار في جميع الأنماط الظاهرية ، يمكنك إلقاء نظرة على نسبة الأصفار والأصفار في كل نمط ظاهري:على الجانب الأيسر من الرسم البياني ، توجد نقاط ذات انحراف كبير عن متوسط القيمة. يمكن افتراض أن هذه هي أوتوماتيا في الأنماط الجينية التي يساوي فيها الجين الصفري الوحدة. من المفترض - فحص. وضعنا الجين صفر يساوي دائما الصفر. نرسم مخطط جديد: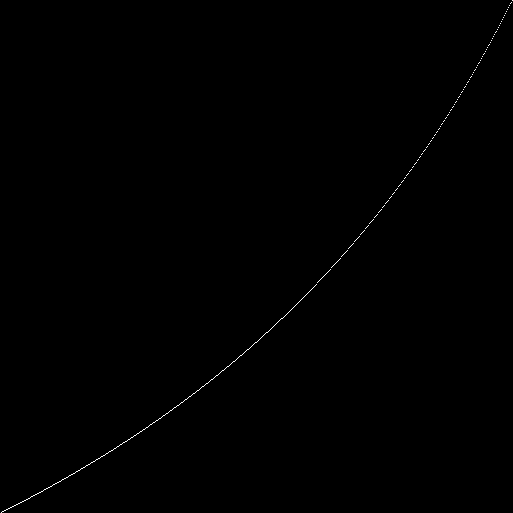
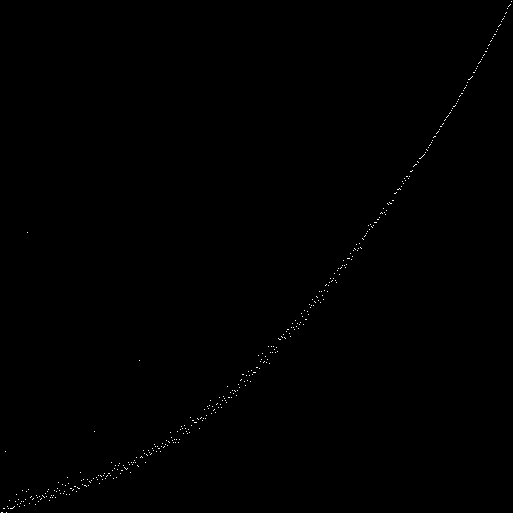

 قارن مع الآلات التي يساوي فيها دائمًا الجين الصفري واحدًا:
قارن مع الآلات التي يساوي فيها دائمًا الجين الصفري واحدًا: في الآلات من الدرجة الثانية ، يوجد جين آخر "صفر" - الجين 512. دعونا نرى كيف يؤثر هذا الجين على النمط الظاهري.دائمًا ما يكون الجين 0 و 512 صفرًا:
في الآلات من الدرجة الثانية ، يوجد جين آخر "صفر" - الجين 512. دعونا نرى كيف يؤثر هذا الجين على النمط الظاهري.دائمًا ما يكون الجين 0 و 512 صفرًا: دائمًا ما يكون الجين صفر. الجين 512 يساوي دائمًا واحدًا:
دائمًا ما يكون الجين صفر. الجين 512 يساوي دائمًا واحدًا: حتى لا يسخر من الصرع المحترم مرة أخرى ، سيتم ملء الجين 0 و 512 بالأصفار في المجموعة الأولية للخوارزمية الجينية.دعونا نلقي نظرة على الآلات التي تخلصنا منها بوضع أصفار على الجينات 0 و 512.الحالات الثماني الأولى من الأوتوماتون التي يتم فيها ملء الجين فقط 0 (الجين الصفري واحد ، والباقي هو الأصفار):
حتى لا يسخر من الصرع المحترم مرة أخرى ، سيتم ملء الجين 0 و 512 بالأصفار في المجموعة الأولية للخوارزمية الجينية.دعونا نلقي نظرة على الآلات التي تخلصنا منها بوضع أصفار على الجينات 0 و 512.الحالات الثماني الأولى من الأوتوماتون التي يتم فيها ملء الجين فقط 0 (الجين الصفري واحد ، والباقي هو الأصفار): الأوتوماتون الذي
الأوتوماتون الذي يتم فيه ملء الجين 512 فقط: هو الأوتوماتون الذي تملأ فيه الجينات 0 و 512 فقط:
يتم فيه ملء الجين 512 فقط: هو الأوتوماتون الذي تملأ فيه الجينات 0 و 512 فقط: لنفرد مكانًا على الرسم البياني حيث يبدأ السكان في التقسيم إلى مجموعات:
لنفرد مكانًا على الرسم البياني حيث يبدأ السكان في التقسيم إلى مجموعات: في هذا المكان ، تمتلئ الأنماط الجينية بنسبة 25٪.قارن بين اثنين من السكان.أول السكان. 30 آلة عشوائية على التكرار 1000. الأنماط الجينية 50٪ كاملة (512 وحدة و 512 أصفار):
في هذا المكان ، تمتلئ الأنماط الجينية بنسبة 25٪.قارن بين اثنين من السكان.أول السكان. 30 آلة عشوائية على التكرار 1000. الأنماط الجينية 50٪ كاملة (512 وحدة و 512 أصفار): المجموعة الثانية. 30 آلة عشوائية على التكرار 1000. الأنماط الوراثية ممتلئة بنسبة 25٪ (256 وحدة و 768 أصفار):
المجموعة الثانية. 30 آلة عشوائية على التكرار 1000. الأنماط الوراثية ممتلئة بنسبة 25٪ (256 وحدة و 768 أصفار): المجموعة الثانية مناسبة للاختيار الاصطناعي. يمكننا بسهولة تسليط الضوء على بعض العلامات في هذه الآلات. على سبيل المثال: "أغمق" ، "أقل فوضى" (الأوتوماتا التي يتم فيها تجميع الخلايا البيضاء) ، إلخ.نختار "أغمق". احتمال حدوث طفرات هو 10 ٪ ، وحتى 4 جينات متحولة. بعد الاختيار الأول:
المجموعة الثانية مناسبة للاختيار الاصطناعي. يمكننا بسهولة تسليط الضوء على بعض العلامات في هذه الآلات. على سبيل المثال: "أغمق" ، "أقل فوضى" (الأوتوماتا التي يتم فيها تجميع الخلايا البيضاء) ، إلخ.نختار "أغمق". احتمال حدوث طفرات هو 10 ٪ ، وحتى 4 جينات متحولة. بعد الاختيار الأول: بعد الاختيار الثاني:
بعد الاختيار الثاني: ظهر ملف آلي مثير للاهتمام في السكان.256 × 256 ، حالة الجهاز في التكرار رقم 1000:
ظهر ملف آلي مثير للاهتمام في السكان.256 × 256 ، حالة الجهاز في التكرار رقم 1000: تملأ الماكينة تدريجيًا السكان.بعد الاختيار الثامن:
تملأ الماكينة تدريجيًا السكان.بعد الاختيار الثامن: ظهرت آلة أخرى مثيرة للاهتمام.256 × 256 ، حالة التشغيل التلقائي في التكرار رقم 1000:
ظهرت آلة أخرى مثيرة للاهتمام.256 × 256 ، حالة التشغيل التلقائي في التكرار رقم 1000: السكان بعد ثلاثة عشر تحديدًا:
السكان بعد ثلاثة عشر تحديدًا: العديد من الصور التلقائية من هذه الفئة. 256 × 256 ، التكرار 1000 للجميع. يوجد أسفل الصورة رابط ، يمكنك النقر فوقه ، ويمكنك إلقاء نظرة على الجهاز في الديناميات:
العديد من الصور التلقائية من هذه الفئة. 256 × 256 ، التكرار 1000 للجميع. يوجد أسفل الصورة رابط ، يمكنك النقر فوقه ، ويمكنك إلقاء نظرة على الجهاز في الديناميات: عرض في الديناميات.
عرض في الديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات. عرض في ديناميات.
عرض في ديناميات.3. كونواي آلة أوتوماتيكية وما شابه ذلك
أشهر لعبة أوتوماتيكية خلوية ثنائية الأبعاد من الدرجة الأولى هي لعبة Conway automaton Game "Life" .تتم كتابة القواعد الخاصة بـ Conway automaton على النحو التالي:إذا كانت هناك 3 خلايا حية حول خلية ميتة ، فإن الخلية تعود إلى الحياة (وإلا تبقى ميتة).إذا كانت هناك خليتان أو ثلاث خلايا حية حول خلية حية ، فستبقى الخلية حية (وإلا تموت).الخلية الميتة هي 0 ، والخلية الحية هي 1.حول الخلية يمكن أن تكون من 0 إلى 8 خلايا حية. وفقا ل 9 خيارات حول الحي وحول الخلية الميتة. نكتب كل الخيارات لمجموعة r:مجموعة ص r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ];
النصف الأول من الصفيف مخصص لخلية ميتة ، والثاني لخلية حية.يمكننا وصف قاعدة كونوتون الآلي لجميع المجموعات (512) الممكنة للخلية و 8 خلايا مجاورة:رسم القاعدة r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; var q1, q2; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[1]+1*ii[2]+1*ii[3]+1*ii[5]+1*ii[6]+1*ii[7]+1*ii[8]; if(q1==0) rule[i]=r[q2]; else rule[i]=r[q2+9]; }
الخيار الأمثل r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; for(var i=0;i<512;i++){ var q=((i>>4)&1)*8; for(var j=0;j<9;j++){ q+=(i>>j)&1; } rule[i]=r[q]; }
لأتمتة الطلب الثاني ، انسخ النصف الثاني من صفيف القاعدة من الأول:نسخة for(var i=0;i<512;i++){ if(rule[i]==0) rule[i+512]=0; else rule[i+512]=1; }
نبدأ الجهاز مع القاعدة المحددة. نرى الطائرات الشراعية والمذبذبات المميزة. عدة تكرارات لهذا الأوتوماتون: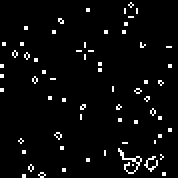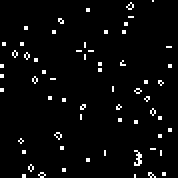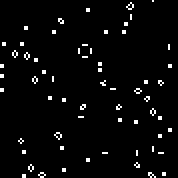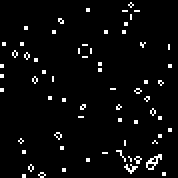 يتكون Array r من 18 خلية. هناك2 18 = 262144 آليًا مشابهًا لأوتوماتية Conway (التي يمكن كتابتها بنفس القواعد: عدد الخلايا الحية المحاطة بالأموات ، والتي تظهر فيها الخلية وعدد الخلايا الحية في البيئة الحية ، والتي تموت فيها الخلية).يمكنك الاطلاع عليهاهنا(افتراضيًا ، يبدأ تشغيل Conway automaton ، يملأ زر "تغيير القاعدة" صفيف r عشوائيًا).هناك عدد قليل من آلات عشوائية (رمز ثنائي - مجموعة ص):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111
يتكون Array r من 18 خلية. هناك2 18 = 262144 آليًا مشابهًا لأوتوماتية Conway (التي يمكن كتابتها بنفس القواعد: عدد الخلايا الحية المحاطة بالأموات ، والتي تظهر فيها الخلية وعدد الخلايا الحية في البيئة الحية ، والتي تموت فيها الخلية).يمكنك الاطلاع عليهاهنا(افتراضيًا ، يبدأ تشغيل Conway automaton ، يملأ زر "تغيير القاعدة" صفيف r عشوائيًا).هناك عدد قليل من آلات عشوائية (رمز ثنائي - مجموعة ص):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111





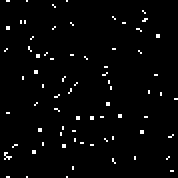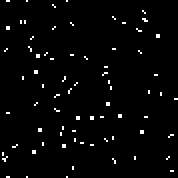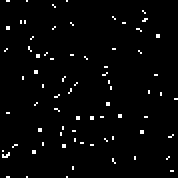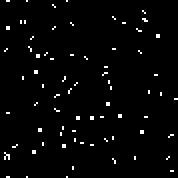

 بالنسبة للخوارزمية الجينية ، كنوع جيني ، يمكنك استخدامها ، كصفيف ص ( 2 18 مجموعات) ، ومجموعة القاعدة (2 512 مجموعات من الدرجة الأولى للإنسان الخلوية و2 1024 - لآلية الخلوية من الدرجة الثانية).2 18 هو عدد صغير نسبيا. يسمح لك هذا الرقم بتحديد القاعدة الخاصة بالجهاز يدويًا ، دون استخدام خوارزمية جينية (في الواقع ، وهو ما فعله كونواي). إذا قمت بملء مصفوفة القواعد بأجهزة عشوائية من هذا النوع واستخدمت هذه المصفوفة كنمط جيني ، فيمكن اعتبار التجربة غير ناجحة ، إلى حد ما (بما يكفي لعدم إظهار نتائج هذه التجربة في المقالة). في قواعد الأتمتة الخلوية من هذا النوع ، هناك تناظر. على سبيل المثال ، لمجموعات الخلايا التالية:
بالنسبة للخوارزمية الجينية ، كنوع جيني ، يمكنك استخدامها ، كصفيف ص ( 2 18 مجموعات) ، ومجموعة القاعدة (2 512 مجموعات من الدرجة الأولى للإنسان الخلوية و2 1024 - لآلية الخلوية من الدرجة الثانية).2 18 هو عدد صغير نسبيا. يسمح لك هذا الرقم بتحديد القاعدة الخاصة بالجهاز يدويًا ، دون استخدام خوارزمية جينية (في الواقع ، وهو ما فعله كونواي). إذا قمت بملء مصفوفة القواعد بأجهزة عشوائية من هذا النوع واستخدمت هذه المصفوفة كنمط جيني ، فيمكن اعتبار التجربة غير ناجحة ، إلى حد ما (بما يكفي لعدم إظهار نتائج هذه التجربة في المقالة). في قواعد الأتمتة الخلوية من هذا النوع ، هناك تناظر. على سبيل المثال ، لمجموعات الخلايا التالية: حالة الخلية في التكرار التالي هي نفسها. بعد المعبر الأول ، يتم كسر التماثل في قواعد الأفراد المنحدرين. الأفراد الأجداد تتراكم الطفرات التي تدمر أيضا التماثل. انتهاك التماثل في النمط الوراثي يؤدي إلى انتهاك التماثل في النمط الظاهري.يمكن للمرء أن يرى مظهر من مظاهر هذا التناظر في النمط الظاهري إذا تم ملء خلية واحدة في الحالة الأولية للأوتوماتون.دعونا نفعل تجربة. للحفاظ على التناظر ، سوف نستخدم صفيف r كنمط جيني. طفرات 5 ٪ ، 1 طفرات الجينات. في الحالة الأولية ، يتم ملء خلية واحدة.30 آلات عشوائية من السكان الأولي. حالة الأتمتة في التكرار الثلاثين:
حالة الخلية في التكرار التالي هي نفسها. بعد المعبر الأول ، يتم كسر التماثل في قواعد الأفراد المنحدرين. الأفراد الأجداد تتراكم الطفرات التي تدمر أيضا التماثل. انتهاك التماثل في النمط الوراثي يؤدي إلى انتهاك التماثل في النمط الظاهري.يمكن للمرء أن يرى مظهر من مظاهر هذا التناظر في النمط الظاهري إذا تم ملء خلية واحدة في الحالة الأولية للأوتوماتون.دعونا نفعل تجربة. للحفاظ على التناظر ، سوف نستخدم صفيف r كنمط جيني. طفرات 5 ٪ ، 1 طفرات الجينات. في الحالة الأولية ، يتم ملء خلية واحدة.30 آلات عشوائية من السكان الأولي. حالة الأتمتة في التكرار الثلاثين: دعونا نحاول عزل الأوتوماتة التي تنمو ببطء (تنمو) من خلية واحدة.
دعونا نحاول عزل الأوتوماتة التي تنمو ببطء (تنمو) من خلية واحدة.



 بعد الاختيار الأول ، تخلصوا من الأوتماتة التي لا تتطور:
بعد الاختيار الأول ، تخلصوا من الأوتماتة التي لا تتطور: في السكان الجدد هناك العديد من الأوتوماتة (التي لا تتطور) - هذه هي أحفاد وطفرات غير ناجحة.بعد ذلك ، سنختار الآلات بشكل رئيسي ذات خلفية بيضاء (خلايا لم يطورها الجهاز).
في السكان الجدد هناك العديد من الأوتوماتة (التي لا تتطور) - هذه هي أحفاد وطفرات غير ناجحة.بعد ذلك ، سنختار الآلات بشكل رئيسي ذات خلفية بيضاء (خلايا لم يطورها الجهاز).آلات بيع سوداء وميض.( — ) — . ( ) ( ). . — () . ( — , — ). 30- , — . ( 30- ) — ( ).
السكان بعد الاختيار الثاني: 3 اختيارات:
3 اختيارات: 5 اختيارات:
5 اختيارات: 8 اختيارات:
8 اختيارات: 13 تحديدات:
13 تحديدات: نفس الآلات في التكرار الستين:
نفس الآلات في التكرار الستين: 21 تحديدًا. حالة automata في التكرار 30:
21 تحديدًا. حالة automata في التكرار 30: حالة automata في التكرار 60:
حالة automata في التكرار 60: 34 التحديدات. حالة الأتمتة في التكرار الثلاثين:
34 التحديدات. حالة الأتمتة في التكرار الثلاثين: حالة الأتمتة في التكرار الستين:
حالة الأتمتة في التكرار الستين: علاوة على ذلك ، لا يتطور النظام. ثلاث أوتوماتات من هذه المجموعة (100 تكرارلكل منها ):
علاوة على ذلك ، لا يتطور النظام. ثلاث أوتوماتات من هذه المجموعة (100 تكرارلكل منها ): [1 ، 1 ، 1 ، 1 ، 1 ، 0 ، 1 ، 0 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ] [1 ، 0،1،1،1،0،0،1،0،0،0،0،0،0،0،0،1،1،1]
[1 ، 1 ، 1 ، 1 ، 1 ، 0 ، 1 ، 0 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ] [1 ، 0،1،1،1،0،0،1،0،0،0،0،0،0،0،0،1،1،1] [1،0،0،1،1،0،0 ] ، 1،1،1،1،0،1،1،0،1،1،1]
[1،0،0،1،1،0،0 ] ، 1،1،1،1،0،1،1،0،1،1،1] للمقارنة ، آلة عشوائية:[1،0،1،1،1،1،0،1،1،0 ، 0،1،1،0،0،0،1]
للمقارنة ، آلة عشوائية:[1،0،1،1،1،1،0،1،1،0 ، 0،1،1،0،0،0،1]
4. كونواي الأوتوماتون وما شابه ذلك (2)
في الآلات التي لها قواعد من نوع Conway ، نحسب عدد الكائنات الحية (الوحدات) من الخلايا بالقرب من مور. يمكن تقسيم هذا الحي إلى 4 أزواج وحساب عدد الخلايا الحية في هذه الأزواج: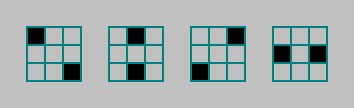 وبالتالي ، فإننا نزيد عدد الأوتوماتة ، ولكن نحافظ على التماثل في النمط الظاهري.يمكن أن يكون لكل زوج من 0 إلى 2 خلايا حية. الاسمية 4. عدد المجموعات3 4 = 81
وبالتالي ، فإننا نزيد عدد الأوتوماتة ، ولكن نحافظ على التماثل في النمط الظاهري.يمكن أن يكون لكل زوج من 0 إلى 2 خلايا حية. الاسمية 4. عدد المجموعات3 4 = 81 .
وفقا لمجموعة 81 حول الحي وحول الخلية الميتة. المجموع موجود2 162 آلات أوتوماتيكية من هذا النوع. عدد:2 162 ≈ 5.846 × 10 48
إنه فلكي تمامًا وسيكون مناسبًا للخوارزمية الجينية.حجم التركيب الوراثي لكل فرد هو 162 جين:ملء السكان مع آلات عشوائية var rulesize=162; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
بعد ذلك ، نرسم هذه القاعدة لجميع المجموعات الممكنة للخلية وثماني خلايا مجاورة:وظيفة fillrule () ؛ function fillrule(){ var r; for(var n=0;n<PopulationSize;n++){ rule[n]=[]; r=population[n]; var q1, q2, q3, q4, q5; var q; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[8]; q3=1*ii[1]+1*ii[7]; q4=1*ii[2]+1*ii[6]; q5=1*ii[3]+1*ii[5]; q=parseInt(''+q2+q3+q4+q5,3); if(q1==0) rule[n][i]=r[q]; else rule[n][i]=r[q+81]; } } }
سنستخدم مجموعة القواعد عند حساب الحالة التالية للأوتوماتون. نحن ندعو وظيفة fillrule () بعد تحميل الصفحة وبعد استدعاء دالة developute ().السكان الأولي يبدو الفوضى. 30 آلة عشوائية ، التكرار رقم 1000: تختلف هذه الفوضى قليلاً في الديناميات والآلات مناسبة تمامًا للاختيار ، لكن لنجعل الأمر أكثر سهولة - سنختار "الأحلك".السكان بعد خمسة اختيارات:
تختلف هذه الفوضى قليلاً في الديناميات والآلات مناسبة تمامًا للاختيار ، لكن لنجعل الأمر أكثر سهولة - سنختار "الأحلك".السكان بعد خمسة اختيارات: بعد ذلك ، يمكنك البحث عن الآلات التي تحتوي على أكثر مؤشرات التذبذب تعقيدًا. العملية برمتها من وضع لا طائل منه. فيما يلي بعض من الأتمتة الأكثر إثارة للاهتمام التي تم العثور عليها باستخدام الخوارزمية الجينية.256 × 256 ، التكرار 10000 للجميع. يوجد أسفل الصورة رابط ، يمكنك النقر فوقه ، ويمكنك إلقاء نظرة على الجهاز في الديناميات:
بعد ذلك ، يمكنك البحث عن الآلات التي تحتوي على أكثر مؤشرات التذبذب تعقيدًا. العملية برمتها من وضع لا طائل منه. فيما يلي بعض من الأتمتة الأكثر إثارة للاهتمام التي تم العثور عليها باستخدام الخوارزمية الجينية.256 × 256 ، التكرار 10000 للجميع. يوجد أسفل الصورة رابط ، يمكنك النقر فوقه ، ويمكنك إلقاء نظرة على الجهاز في الديناميات: عرض في الديناميات.
عرض في الديناميات. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.?
ويمكنك أن تلعب هنا: لعبةأوتوماتيكية ثنائية الأبعاد من الدرجة الثانية.واجهة: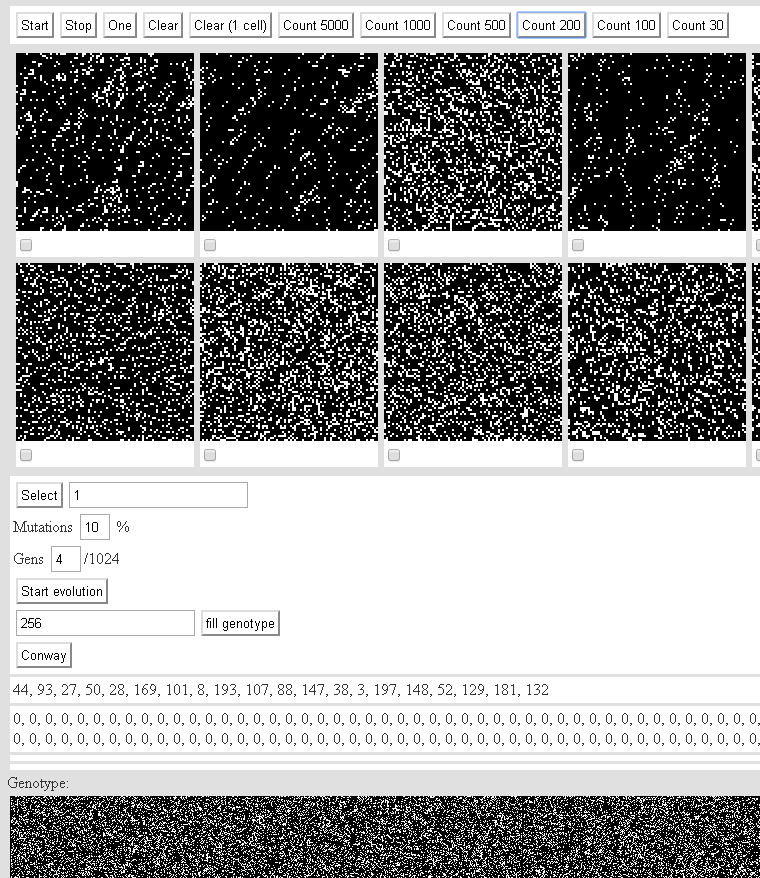 زر ابدأ يبدأ الآلات.توقف - توقف.واحد هو التكرار واحد.مسح - يوقف الجهاز ويملأ الحالة الأولية بعشوائية.مسح (خلية واحدة) - يوقف الجهاز ويملأ خلية واحدة في الحالة الأولية.تحسب الأزرار المتبقية على هذا الخط العدد المحدد من التكرارات لكل آلية.تقديم أداء آلي على القماش يستوعب كل الأداء. إذا كنت بحاجة إلى حساب 200 تكرار سريعًا - انقر فوق Count 200. لا نقر فوق الزر Count 5000 - يمكن للمتصفح تعليقه.أقل من 20 آلة عشوائية (حجم السكان - 200 آلات). تحت خانات البيع آلات البيع. نحتفل الأكثر إثارة للاهتمام. اضغط على "تحديد" - ستزداد ملاءمة الماكينة عن طريق الرقم المحدد على اليمين.الطفرات - احتمال حدوث طفرات.جين هو عدد الجينات المتحورة.بدء التطور - تطلق آلية الصلبان والطفرات.تعبئة النمط الوراثي - يملأ العدد المحدد من الجينات في التركيب الوراثي لكل آلية.كونواي - تملأ السكان باستخدام آلات نوع Konveevsky.فيما يلي سطرين:أرقام الآلات المعروضة.محتويات الصفيف fenotype.مجموعة الجينات من السكان أقل.يتم تخزين كل التقدم في التخزين المحلي.يمكنك أن تلعب مع بنادق هجومية من نوع Konveevsky (مع تلك التي كانت تعتبر الأخيرة في المقال) هنا:4. Conway automaton وما شابه (2).
زر ابدأ يبدأ الآلات.توقف - توقف.واحد هو التكرار واحد.مسح - يوقف الجهاز ويملأ الحالة الأولية بعشوائية.مسح (خلية واحدة) - يوقف الجهاز ويملأ خلية واحدة في الحالة الأولية.تحسب الأزرار المتبقية على هذا الخط العدد المحدد من التكرارات لكل آلية.تقديم أداء آلي على القماش يستوعب كل الأداء. إذا كنت بحاجة إلى حساب 200 تكرار سريعًا - انقر فوق Count 200. لا نقر فوق الزر Count 5000 - يمكن للمتصفح تعليقه.أقل من 20 آلة عشوائية (حجم السكان - 200 آلات). تحت خانات البيع آلات البيع. نحتفل الأكثر إثارة للاهتمام. اضغط على "تحديد" - ستزداد ملاءمة الماكينة عن طريق الرقم المحدد على اليمين.الطفرات - احتمال حدوث طفرات.جين هو عدد الجينات المتحورة.بدء التطور - تطلق آلية الصلبان والطفرات.تعبئة النمط الوراثي - يملأ العدد المحدد من الجينات في التركيب الوراثي لكل آلية.كونواي - تملأ السكان باستخدام آلات نوع Konveevsky.فيما يلي سطرين:أرقام الآلات المعروضة.محتويات الصفيف fenotype.مجموعة الجينات من السكان أقل.يتم تخزين كل التقدم في التخزين المحلي.يمكنك أن تلعب مع بنادق هجومية من نوع Konveevsky (مع تلك التي كانت تعتبر الأخيرة في المقال) هنا:4. Conway automaton وما شابه (2).