كيفية حل المشاكل NP- الثابت باستخدام خوارزميات معلمة

العمل البحثي ربما يكون الجزء الأكثر إثارة للاهتمام من التدريب لدينا. الفكرة هي أن تجرب نفسك في الاتجاه المختار حتى في الجامعة. على سبيل المثال ، غالبًا ما يذهب الطلاب من مجالات هندسة البرمجيات والتعلم الآلي لإجراء الأبحاث في الشركة (لا سيما JetBrains أو Yandex ، ولكن ليس فقط).

في هذا المنشور سأتحدث عن مشروعي في علوم الكمبيوتر. كجزء من العمل ، درست ووضعت أساليب عملية لحل واحدة من أشهر المشكلات التي يصعب حلها بالبروتين NP: مشكلة تغطية الرأس .

الآن نهج مثير للاهتمام للمشاكل NP الصعب تتطور بسرعة - خوارزميات المعلمات. سأحاول أن أجعلك تصل إلى السرعة ، وأخبر بعض الخوارزميات البسيطة ذات المعلمات وأصف إحدى الطرق القوية التي ساعدتني كثيرًا. قدمت نتائجي في تحدي PACE: وفقًا لنتائج الاختبارات المفتوحة ، يكون قراري في المركز الثالث ، وستكون النتائج النهائية معروفة في 1 يوليو.

عن نفسي

اسمي فاسيلي ألفيروف ، أكمل الآن السنة الثالثة من الصحة والسلامة - سانت بطرسبرغ. لقد كنت مولعا بالخوارزميات منذ أوقات الدراسة ، عندما درست في مدرسة موسكو 179 وشاركت بنجاح في مسابقات علوم الكمبيوتر.

يذهب العدد النهائي للمتخصصين في الخوارزميات المعلمة إلى الشريط ...

مثال مأخوذ من كتاب "خوارزميات معلمة"

تخيل أنك حارس بار في بلدة صغيرة. كل يوم جمعة ، يأتي نصف المدينة إلى الحانة للاسترخاء ، مما يمنحك الكثير من المتاعب: تحتاج إلى طرد الزائرين العنيفين من الحانة لمنع المعارك. في النهاية ، تزعجك وتقرر اتخاذ تدابير وقائية.

نظرًا لأن مدينتك صغيرة ، فأنت تعرف بالتأكيد أي أزواج من الزوار من المحتمل أن يتشاجروا إذا وصلوا إلى الشريط معًا. لديك قائمة بالأشخاص الذين سيأتون إلى البار الليلة. أنت تقرر عدم السماح لأي من سكان البلدة بالدخول إلى الحانة حتى لا يحارب أحد. في الوقت نفسه ، لا يرغب رؤسائك في خسارة الأرباح ولن يكونوا سعداء إذا لم تدع أكثر من k يذهبون إلى الحانة.

لسوء الحظ ، فإن التحدي الذي تواجهه هو مهمة NP الصعب الكلاسيكية. يمكنك معرفة ذلك باسم غطاء الرأس أو مشكلة تغطية الرأس. لمثل هذه المشاكل ، في الحالة العامة ، الخوارزميات التي تعمل في وقت مقبول غير معروفة. على وجه الدقة ، تقول فرضية غير مثبتة وقوية إلى حد ما ETH (فرضية الوقت الأسي) أن هذه المشكلة لا يمكن حلها في الوقت المناسب $$$2 ^ {o (n)}$، وهذا هو ، ما هو أفضل بشكل ملحوظ من البحث الشامل لا يمكن التفكير فيه. على سبيل المثال ، دع n = 1000 شخص يخططون للحضور إلى الحانة. ثم البحث الكامل سيكون $$$2 ^ {1000}$الخيارات التي توجد تقريبا $$$10 ^ {301}$- بجنون كثيرا. لحسن الحظ ، حدد لك دليلك حدًا = 10 ، وبالتالي فإن عدد المجموعات التي تحتاج إلى تكرارها أقل من ذلك بكثير: عدد المجموعات الفرعية المكونة من عشرة عناصر هو $$ . هذا بالفعل أفضل ، لكنه لا يزال غير مهم لهذا اليوم ، حتى في مجموعة قوية.

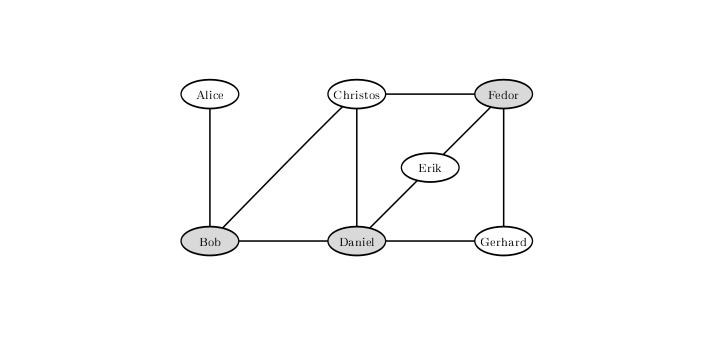
لاستبعاد احتمال حدوث قتال مع مثل هذا النوع من العلاقات المتوترة بين زوار الشريط ، يجب ألا تدع بوب ودانيال وفيدور. الحل الذي لم يتبق منه سوى اثنين فقط.

هل هذا يعني أن الوقت قد حان للاستسلام والسماح للجميع بالدخول؟ لننظر في الخيارات الأخرى. حسنًا ، على سبيل المثال ، لا يمكنك السماح فقط بدخول الأشخاص الذين يحتمل أن يقاتلوا مع عدد كبير جدًا من الأشخاص. إذا كان بإمكان شخص ما القتال على الأقل مع k + 1 من قِبل شخص آخر ، فعندئذ لا يمكنك بالتأكيد السماح له بالدخول ، وإلا فسيتعين عليك إبعاد جميع مواطني k + 1 عن الذين يمكنك القتال معهم ، مما سيؤدي بالتأكيد إلى إزعاج القيادة.

قد تطرد كل ما تستطيع وفقا لهذا المبدأ. ثم يمكن لأي شخص آخر القتال مع أكثر من ك الناس. رمي ك الناس للخروج منها ، لا يمكنك منع أكثر من $$$ك ^ 2 دولا$الصراعات. لذلك ، إذا كان كل شيء أكثر من $$$2k ^ 2$إذا كان شخص ما متورطا في نزاع واحد على الأقل ، فمن المؤكد أنك لا تستطيع منعهم جميعا. نظرًا لأنك بالطبع ستسمح للناس الذين لا ينتمون إلى صراع بالرحيل تمامًا ، فأنت بحاجة إلى فرز جميع المجموعات الفرعية بحجم عشرة من كل مائتي شخص. هناك تقريبا $$$2.24 \ cdot 10 ^ {16}$، ويمكن بالفعل فرز العديد من العمليات على الكتلة.

إذا كان من الآمن أخذ شخصيات غير متعارضة تمامًا ، فماذا عن الأشخاص المتورطين في صراع واحد فقط؟ في الواقع ، يمكن أيضًا السماح لهم بإغلاق الأبواب أمام خصمهم. في الواقع ، إذا كان أليس يتعارض فقط مع بوب ، ثم إذا تركنا اثنين منهم في أليس ، فلن نخسر: قد يكون لدى بوب صراعات أخرى ، لكن أليس بالتأكيد ليس لديهم. علاوة على ذلك ، فليس من المنطقي بالنسبة لنا ألا نسمح لكليهما. بعد هذه العمليات ، لا أكثر $$$ك ^ 2 دولا$الضيوف مع مصير لم تحل: كل ما لدينا $$$ك ^ 2 دولا$الصراعات ، في كل من مشاركين وكل مشارك في اثنين على الأقل. لذلك ، يبقى فقط للفرز $$$1.73 \ cdot 10 ^ {13}$الخيارات ، والتي قد يتم حسابها بشكل جيد لمدة نصف يوم على جهاز كمبيوتر محمول.

في الواقع ، يمكن أن يحقق المنطق البسيط ظروفًا أكثر جاذبية. لاحظ أننا نحتاج بالتأكيد إلى حل جميع النزاعات ، أي من كل زوج متضارب لاختيار شخص واحد على الأقل لن نسمح له بالدخول. ضع في اعتبارك هذه الخوارزمية: خذ أي تعارض نحذف منه أحد المشاركين ونبدأ بشكل متكرر من الباقي ، ثم احذف آخر ونبدأ أيضًا بشكل متكرر. نظرًا لأننا نرمي شخصًا ما في كل خطوة ، فإن شجرة العودية لهذه الخوارزمية هي شجرة ثنائية بعمق k ، وبالتالي ، فإن الخوارزمية تعمل بشكل عام $$$2 ^ k⋅ (n + m)$حيث n هو عدد القمم و m هو عدد الحواف. في مثالنا ، هذا هو حوالي عشرة ملايين ، والتي سيتم احتسابها في الثانية الواحدة ليس فقط على جهاز كمبيوتر محمول ، ولكن حتى على هاتف محمول.

المثال أعلاه هو مثال لخوارزمية ذات معلمات . الخوارزميات الباراميترية هي خوارزميات تعمل خلال f (k) poly (n) ، حيث p متعددة الحدود ، و f هي دالة حسابية تعسفية ، و k هي بعض المعلمات التي ، ربما تكون أصغر بكثير من حجم المشكلة.

تقدم جميع المناقشات التي سبقت هذه الخوارزمية مثالًا على kernelization ، أحد الأساليب الشائعة لإنشاء خوارزميات ذات معلمات. Kernelization هو تقليل حجم المهمة إلى قيمة محددة بواسطة دالة المعلمة. المهمة الناتجة غالبًا تسمى kernel. لذلك ، من خلال التفكير البسيط حول درجات القمم ، حصلنا على نواة تربيعية لمشكلة الغطاء Vertex ، والتي تم تحديد حجمها بحجم الإجابة. هناك معلمات أخرى يمكن اختيارها لهذه المهمة (على سبيل المثال ، Vertex Cover Above LP) ، لكننا سنناقش مثل هذه المعلمة فقط.

التحدي بيس

بدأت مسابقة PACE Challenge (الخوارزميات المعلمة وتحدي التجارب الحسابية) في عام 2015 لإقامة صلة بين الخوارزميات ذات المعلمات والنُهج المستخدمة في الممارسة العملية لحل المشكلات الحسابية. تم تخصيص المسابقات الثلاثة الأولى للعثور على عرض شجرة الرسم البياني ( Treewidth ) ، والعثور على Steiner Tree ( Steiner Tree ) وإيجاد العديد من القمم ، ودورات القطع ( Feedback Vertex Set ). في هذا العام ، كانت إحدى المشكلات التي يمكن للمرء أن يجرب فيها مواطن القوة هي مشكلة الغطاء العلوي الموصوف أعلاه.

المنافسة تكتسب شعبية كل عام. إذا كنت تعتقد أن البيانات الأولية ، فإن 24 فريقًا فقط شاركوا في المسابقة هذا العام لحل مشكلة تغطية قمة الرأس. تجدر الإشارة إلى أن المنافسة لا تدوم عدة ساعات ، ولا حتى أسبوع ، ولكن عدة أشهر. لدى الفرق فرصة لدراسة الأدب والتوصل إلى فكرتهم الأصلية ومحاولة تنفيذها. في الواقع ، هذه المسابقة هي عمل بحثي. سيتم عقد أفكار للحلول الأكثر فاعلية ومنح الفائزين بالتزامن مع مؤتمر IPEC (الندوة الدولية حول الحوسبة الدقيقة والحساب الدقيق) في أكبر اجتماع خوارزمي سنوي في أوروبا ALGO . يمكن العثور على مزيد من المعلومات حول المسابقة نفسها على الموقع الإلكتروني ، ونتائج السنوات الماضية موجودة هنا .

مخطط الحل

للتعامل مع مشكلة تغطية قمة الرأس ، حاولت تطبيق خوارزميات معلمة. تتكون عادةً من جزأين: قواعد التبسيط (التي تؤدي بشكل مثالي إلى تقنين الأحرف) وتقسيم القواعد. قواعد التبسيط هي إدخال ما قبل المعالجة في كثير الحدود. الغرض من تطبيق هذه القواعد هو تقليل المشكلة إلى مشكلة مكافئة ذات حجم أصغر. قواعد التبسيط هي أغلى جزء من الخوارزمية ، ويؤدي تطبيق هذا الجزء المعين إلى إجمالي وقت العمل $$$c ^ k⋅poly (n)$بدلا من الوقت متعدد الحدود بسيط. في حالتنا ، تستند قواعد الفصل إلى حقيقة أن كل قمة تحتاج إلى أخذ جارها أو جوابها كرد فعل.

المخطط العام هو هذا: نحن نطبق قواعد التبسيط ، ثم نختار بعض الرأس ، ونجري نداءين متكررين: في البداية نأخذها استجابة ، وفي الآخر نأخذ جميع جيرانها. هذا هو ما نسميه تقسيم (الغداء) على طول هذه الذروة.

بالضبط سيتم إضافة واحدة لهذا المخطط في الفقرة التالية.

أفكار لتقسيم القواعد

دعونا نناقش كيفية اختيار قمة الرأس التي سيحدث فيها الانقسام.
الفكرة الرئيسية جشعة جدًا بالمعنى الحسابي: فلنأخذ ذروة الدرجة القصوى ونقسمها. لماذا يبدو أفضل؟ لأنه في الفرع الثاني من المكالمة العودية ، سنقوم بإزالة العديد من القمم بهذه الطريقة. يمكنك توقع بقاء رسم بياني صغير وسنعمل عليه بسرعة.

هذا النهج ، مع التقنيات البسيطة التي تمت مناقشتها بالفعل ، ليس سيئًا ، فهو يحل بعض الاختبارات بحجم عدة آلاف من الرؤوس. ولكن ، على سبيل المثال ، لا يعمل بشكل جيد بالنسبة للرسوم البيانية المكعبة (أي الرسوم البيانية التي تكون درجة كل قمة منها ثلاثة).
هناك فكرة أخرى تستند إلى فكرة بسيطة إلى حد ما: إذا تم فصل الرسم البياني ، فيمكن حل المشكلة على المكونات المتصلة به بشكل مستقل من خلال الجمع بين الإجابات في النهاية. هذا ، بالمناسبة ، هو التعديل الموعود البسيط في المخطط ، والذي سيسرع بشكل كبير في الحل: في وقت سابق في هذه الحالة ، عملنا من أجل منتج لأوقات حساب استجابات المكونات ، والآن نحن نعمل من أجل المبلغ. ولتسريع عملية الغداء ، تحتاج إلى تحويل رسم بياني متصل إلى رسم منفصل.

كيف نفعل ذلك؟ إذا كانت هناك نقطة توضيح في الرسم البياني ، فمن الضروري أن تتجول فيها. نقطة التوضيح هي قمة الرأس ، عند إزالتها ، يفقد الرسم البياني الاتصال. ابحث في الرسم البياني عن أن جميع نقاط المفصل يمكن أن تكون خوارزمية كلاسيكية في الوقت الخطي. هذا النهج يسرع بشكل كبير الغداء.

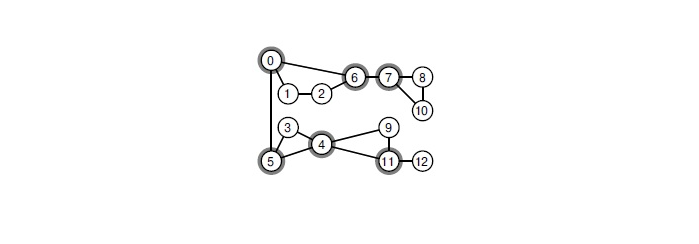
عندما تقوم بإزالة أي من الرؤوس المحددة ، فإن الرسم البياني يتحلل إلى مكونات متصلة.

سنفعل ذلك ، لكنني أريد المزيد. على سبيل المثال ، ابحث عن أقسام رأس صغيرة في الرسم البياني وانقسام على طول القمم منه. الطريقة الأكثر فعالية التي أعرفها للعثور على الحد الأدنى لقسم قمة الرأس العالمي هي استخدام شجرة Gomori-Hu ، التي بنيت في وقت مكعب. في تحدي PACE ، يبلغ حجم الرسم البياني النموذجي عدة آلاف من الرؤوس. في هذا السيناريو ، يجب إجراء مليارات العمليات في كل قمة من شجرة العودية. اتضح أنه من المستحيل ببساطة حل المشكلة في الوقت المخصص.

دعونا نحاول تحسين الحل. يمكن العثور على القسم الأدنى من قمة الرأس بين زوج من القمم بواسطة أي خوارزمية تقوم بإنشاء الحد الأقصى للتدفق. يمكنك تشغيل خوارزمية Dinitz على مثل هذه الشبكة ؛ وفي الممارسة العملية ، تعمل بسرعة كبيرة. لدي شكوك أنه من الناحية النظرية ، يمكن إثبات تقدير وقت العمل $$$مليون ^ {1/2}$هذا بالفعل مقبول تماما.

حاولت عدة مرات البحث عن قطع بين أزواج من القمم العشوائية وأخذ أكثرها توازناً منها. لسوء الحظ ، في اختبارات PACE Challenge المفتوحة ، أعطى هذا نتائج سيئة. قارنته بخوارزمية كانت متناثرة على طول القمم بأقصى درجة ، وبدأتها بفرض قيود على عمق النسب. بعد محاولة الخوارزمية العثور على القطع بهذه الطريقة ، بقيت الرسوم البيانية أكبر. هذا يرجع إلى حقيقة أن التخفيضات تبين أنها غير متوازنة للغاية: بعد إزالة 5-10 قمم ، فقط 15-20 كانت قادرة على الانقسام.

تجدر الإشارة إلى أن مقالات حول أسرع الخوارزميات من الناحية النظرية تستخدم تقنيات أكثر تطوراً لاختيار الرؤوس للتقسيم. هذه التقنيات لها تنفيذ معقد للغاية وغالبًا ما تكون درجات الوقت والذاكرة ضعيفة. لم أستطع التمييز بينها مقبولًا تمامًا للممارسة.

كيفية تطبيق قواعد التبسيط

لدينا بالفعل أفكار للنواة. دعني أذكرك:

1. إذا كان هناك قمة معزولة ، فاحذفها.
2. إذا كان هناك قمة من الدرجة 1 ، فاحذفها وأخذ جارها في الرد.
3. إذا كان هناك قمة درجة لا تقل عن K + 1 ، خذها كرد فعل.

مع أول اثنين كل شيء واضح ، والثالث هناك خدعة واحدة. إذا كان لدينا مشكلة في الشريط الهزلي حصلنا على قيود من الأعلى على k ، ثم في تحدي PACE ، ستحتاج فقط إلى العثور على غطاء رأس الحد الأدنى للحجم. هذا تحويل نموذجي لمشكلة البحث إلى مشكلة قرار ، غالبًا بين نوعين من المهام التي لا تحدث فرقًا بينهما. في الممارسة العملية ، إذا كتبنا حل مشكلة تغطية قمة الرأس ، فقد يكون هناك اختلاف. على سبيل المثال ، كما في الفقرة الثالثة.

من حيث التنفيذ ، هناك طريقتان للقيام بذلك. ويسمى النهج الأول تكراري تعميق. يتألف الأمر مما يلي: يمكننا أن نبدأ ببعض القيود المعقولة من الأسفل على الإجابة ، ثم نقوم بتشغيل الخوارزمية الخاصة بنا ، باستخدام هذا التقييد كقيد على الإجابة الواردة أعلاه ، دون النزول في تكرار أقل من هذا التقييد. إذا وجدنا بعض الإجابات ، فمن المؤكد أنها ستكون الأمثل ، وإلا يمكنك زيادة هذا الحد بواحد والبدء من جديد.

هناك طريقة أخرى تتمثل في تخزين بعض الإجابات المثلى الحالية والبحث عن إجابة أصغر ، عند العثور عليها ، قم بتغيير هذه المعلمة k لقطع فروع الزائدة في البحث أكثر.

بعد إجراء العديد من التجارب الليلية ، استقرت على مزيج من هاتين الطريقتين: أولاً ، أقوم بتشغيل خوارزمية بنوع من التقييد على عمق البحث (باختياره بحيث يستغرق وقتًا ضئيلًا مقارنةً بالحل الرئيسي) واستخدم أفضل حل تم العثور عليه كقيد من الأعلى للإجابة - وهذا هو ، لذلك ك جدا.

رؤوس الدرجة 2

برؤوس درجات 0 و 1 برزت. اتضح أنه يمكن أيضًا القيام بذلك برؤوس من الدرجة 2 ، ولكن لهذا ، سيتطلب الرسم البياني عمليات أكثر تعقيدًا.

لشرح هذا ، تحتاج إلى تحديد القمم بطريقة أو بأخرى. نحن نسمي قمة الرأس من الدرجة 2 ، قمة الرأس ، وجيرانها الرؤوس س و ص . ثم سيكون لدينا حالتين.

1. عندما x و y هي الجيران. ثم يمكنك أن تأخذ ردا x و y ، وحذف v . في الواقع ، يجب أن تؤخذ قارتان على الأقل من هذا المثلث رداً ولن نفقد بالتأكيد إذا أخذنا x و y : ربما يكون لديهم جيران أكثر ، لكن v لا.
2. عندما x و y ليسا جيران. ثم يذكر أنه يمكن لصق جميع القمم الثلاثة معا في واحد. والفكرة هي أنه في هذه الحالة ، توجد إجابة مثالية نأخذ فيها إما v أو كلاهما x و y . علاوة على ذلك ، في الحالة الأولى يتعين علينا أن نأخذ ردا على جميع الجيران x و y ، وفي الحالة الثانية ، ليس من الضروري. هذا هو الحال بالضبط عندما لا نأخذ قمة الرأس الملصقة استجابةً وعندما نأخذها. يبقى فقط أن نلاحظ أنه في كلتا الحالتين تتناقص الاستجابة من مثل هذه العملية بواحد.

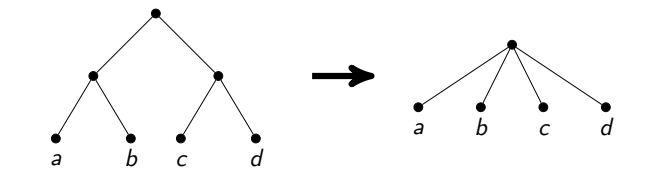
تجدر الإشارة إلى أن هذا النهج للوقت الخطي الصادق يصعب تنفيذه بدقة. رؤوس الإلتصاق هي عملية صعبة ، تحتاج إلى نسخ قوائم الجيران. إذا قمت بذلك بلا مبالاة ، فيمكنك الحصول على وقت تشغيل غير مثلى (على سبيل المثال ، إذا قمت بنسخ الكثير من الحواف بعد كل عملية لاصق). لقد استقرت على البحث عن مسارات كاملة من رؤوس الدرجة 2 وتحليل مجموعة من الحالات الخاصة ، مثل حلقات من هذه الرؤوس أو من كل هذه الرؤوس باستثناء واحدة.

بالإضافة إلى ذلك ، من الضروري أن تكون هذه العملية قابلة للعكس ، حتى نتمكن من استعادة الرسم البياني في شكله الأصلي أثناء العودة من التكرار. لضمان ذلك ، لم أقم بمسح قوائم حواف الرؤوس المدمجة ، وبعد ذلك عرفت فقط الحواف التي ينبغي توجيهها إليها. يتطلب تطبيق الرسوم البيانية هذا أيضًا دقة ، ولكنه يوفر وقتًا خطيًا صادقًا. وبالنسبة إلى الرسوم البيانية التي تحتوي على عدة عشرات الآلاف من الحواف ، يتم ملاءمتها تمامًا في ذاكرة التخزين المؤقت للمعالج ، مما يوفر ميزات سرعة فائقة.

خطي الأساسية

وأخيرا ، الجزء الأكثر إثارة للاهتمام من النواة.

أولاً ، تذكر أنه في الرسوم البيانية ثنائية الأطراف ، يمكن البحث عن الحد الأدنى من تغطية قمة الرأس $$$مليون ^ {1/2}$. للقيام بذلك ، استخدم خوارزمية Hopcroft-Karp للعثور على الحد الأقصى المطابق هناك ، ثم استخدم نظرية Koenig-Egerwari .

فكرة النواة الخطية هي كما يلي: أولاً ، نقسم الرسم البياني ، أي أننا نحصل على رأسين بدلاً من كل قمة $$$v_L$و $$$v_R$وبدلاً من كل حافة u - لدينا حافتان $$$u_L - v_R$و $$$v_L - u_R$. سوف يكون الرسم البياني الناتج ثنائي القطب. نجد فيه الحد الأدنى من تغطية قمة الرأس. بعض قمم الرسم البياني الأصلي تصل إلى هناك مرتين ، بعضها مرة واحدة فقط ، والبعض الآخر لا يحدث مرة واحدة. تنص نظرية Nemhauser-Trotter على أنه في هذه الحالة يمكن إزالة القمم التي لم يتم ضربها مرة واحدة وللرد على تلك التي ضربتها مرتين. علاوة على ذلك ، تقول إنه من بين القمم المتبقية (تلك التي ضربت مرة واحدة) ، عليك أن تأخذ نصف الظهر على الأقل.

لقد تعلمنا فقط ألا نترك أكثر من 2 كيلو رأس في الرسم البياني. في الواقع ، إذا كانت بقية الإجابة على الأقل نصف جميع القمم ، فإن إجمالي القمم لا يزيد عن 2 ك .

تمكنت هنا من اتخاذ خطوة صغيرة إلى الأمام. من الواضح أن النواة التي شيدت بهذه الطريقة تعتمد على نوع الحد الأدنى من تغطية قمة الرأس في الرسم البياني ثنائي الأطراف الذي أخذناه. أود أن أغتنم بحيث يكون عدد الرؤوس المتبقية ضئيلاً. سابقا ، كانوا يعرفون فقط كيفية القيام بذلك في الوقت المناسب. $$$مليون ^ {3/2}$. خطرت لي تنفيذ هذه الخوارزمية في الوقت المناسب $$$مليون ^ {1/2}$وبالتالي ، يمكن البحث في هذا الأساسية على الرسوم البيانية لمئات الآلاف من القمم في كل مرحلة من مراحل المتفرعة.

يؤدي

تدل الممارسة على أن الحل الخاص بي يعمل بشكل جيد على اختبارات مئات الرؤوس وعدة آلاف من الحواف. في مثل هذه الاختبارات ، يمكن توقع إيجاد حل خلال نصف ساعة. يزيد احتمال العثور على إجابة في فترة زمنية مقبولة من حيث المبدأ إذا كان للرسم البياني الكثير من القمم بدرجة كبيرة ، على سبيل المثال ، الدرجات 10 وما فوق.

للمشاركة في المسابقة ، يجب إرسال القرارات إلى optil.io . استنادا إلى اللوحة المقدمة هناك ، فإن قراري بشأن الاختبارات المفتوحة يحتل المرتبة الثالثة من بين العشرين بهامش واسع من الثانية. لكي أكون صادقًا تمامًا ، ليس من الواضح تمامًا كيف سيتم تقييم القرارات في المسابقة نفسها: على سبيل المثال ، يجتاز قراري اختبارات أقل من القرار في المركز الرابع ، لكنه يعمل بشكل أسرع بالنسبة لأولئك الذين يمرون.

سيتم الإعلان عن نتائج الاختبارات المغلقة في 1 يوليو.