مرحبًا بك في واحدة من المحاضرات في CS231n: الشبكات العصبية التلافيفية للتعرف البصري .

محتوى

• نظرة عامة على الهندسة المعمارية
• طبقات في شبكة عصبية تلافيفية
  - طبقة تلافيفية
  - الطبقة الفرعية
  - طبقة التطبيع
  - طبقة متصلة بالكامل
  - تحويل الطبقات المتصلة بالكامل إلى طبقات تلافيفية
• هندسة الشبكات العصبية التلافيفية
  - قوالب الطبقة
  - أنماط حجم الطبقة
  - دراسة حالة (LeNet و AlexNet و ZFNet و GoogLeNet و VGGNet)
  - الجوانب الحسابية
• مزيد من القراءة

الشبكات العصبية التلافيفية (CNN / ConvNets)

تتشابه الشبكات العصبية التلافيفية إلى حد كبير مع الشبكات العصبية العادية التي درسناها في الفصل الأخير (بالإشارة إلى الفصل الأخير من الدورة التدريبية CS231n): فهي تتكون من عصبونات ، والتي بدورها تحتوي على أوزان ونزوح متغير. تستقبل كل خلية عصبية بعض بيانات الإدخال ، وتحسب المنتج القياسي ، وتستخدم اختياريًا وظيفة التنشيط غير الخطية. الشبكة بأكملها ، كما كان من قبل ، هي وظيفة التقييم الوحيدة القابلة للتمييز: من المجموعة الأولية من البكسل (الصورة) في نهاية إلى التوزيع الاحتمالي للانتماء إلى فئة معينة في الطرف الآخر. لا تزال هذه الشبكات لها وظيفة فقد (على سبيل المثال ، SVM / Softmax) على آخر طبقة (متصلة بالكامل) ، وجميع النصائح والتوصيات التي قدمت في الفصل السابق فيما يتعلق بالشبكات العصبية العادية لها صلة أيضًا بالشبكات العصبية التلافيفية.

إذن ما الذي تغير؟ تتضمن بنية الشبكات العصبية التلافيفية بشكل صريح الحصول على صور عند الإدخال ، مما يسمح لنا بمراعاة بعض خصائص بيانات الإدخال في بنية الشبكة نفسها. تتيح لك هذه الخصائص تنفيذ وظيفة التوزيع المباشر بشكل أكثر كفاءة وتقليل إجمالي عدد المعلمات في الشبكة بشكل كبير.

نظرة عامة على الهندسة المعمارية

نحن نتذكر الشبكات العصبية العادية. كما رأينا في الفصل السابق ، تستقبل الشبكات العصبية بيانات الإدخال (متجه واحد) وتحولها عن طريق "الدفع" عبر سلسلة من الطبقات المخفية . تتكون كل طبقة مخفية من عدد معين من الخلايا العصبية ، يرتبط كل منها بكل الخلايا العصبية في الطبقة السابقة وحيث تكون الخلايا العصبية في كل طبقة مستقلة تمامًا عن الخلايا العصبية الأخرى في نفس المستوى. آخر طبقة متصلة بالكامل تسمى "طبقة المخرجات" وفي مشاكل التصنيف ، يتم توزيع الدرجات حسب الفصل.

الشبكات العصبية التقليدية لا تتناسب بشكل جيد مع الصور الكبيرة . في مجموعة البيانات CIFAR-10 ، الصور بحجم 32 × 32 × 3 (32 بكسل ، عرض 32 بكسل ، 3 قنوات ملونة). لمعالجة مثل هذه الصورة ، سيكون للخلايا العصبية المتصلة بالكامل في الطبقة المخفية الأولى من الشبكة العصبية العادية 32 × 32 × 3 = 3072 أوزان. لا يزال هذا المبلغ مقبولًا ، لكن يتضح أن مثل هذا الهيكل لن يعمل مع الصور الأكبر حجمًا. على سبيل المثال ، ستتسبب الصورة الأكبر - 200 × 200 × 3 ، في أن يصبح عدد الأوزان 200 × 200 × 3 = 120.000. وعلاوة على ذلك ، سنحتاج إلى أكثر من خلية من هذه الخلايا العصبية ، لذلك سيبدأ نمو إجمالي عدد الأوزان بسرعة. يصبح من الواضح أن الاتصال مفرط وأن عددًا كبيرًا من المعلمات سيقود الشبكة بسرعة إلى إعادة التدريب.

3D تمثيل الخلايا العصبية . تستخدم الشبكات العصبية التلافيفية حقيقة أن بيانات المدخلات هي صور ، لذا فهي تشكل بنية أكثر حساسية لهذا النوع من البيانات. على وجه الخصوص ، خلافًا للشبكات العصبية العادية ، ترتب الطبقات في الشبكة العصبية التلافيفية الخلايا العصبية في 3 أبعاد - العرض والطول والعمق ( ملاحظة : تشير كلمة "العمق" إلى البعد الثالث لخلايا العصبونات التنشيطية وليس عمق الشبكة العصبية نفسها المقاسة بـ عدد الطبقات). على سبيل المثال ، الصور المدخلة من مجموعة بيانات CIFAR-10 هي بيانات إدخال في تمثيل ثلاثي الأبعاد ، البعد هو 32 × 32 × 3 (العرض ، الارتفاع ، العمق). كما سنرى لاحقًا ، سيتم ربط الخلايا العصبية في طبقة واحدة بعدد صغير من الخلايا العصبية في الطبقة السابقة ، بدلاً من الاتصال بجميع الخلايا العصبية السابقة في الطبقة. علاوة على ذلك ، سيكون لطبقة إخراج الصورة من مجموعة بيانات CIFAR-10 بعد 1 × 1 × 10 ، لأنه عندما نقترب من نهاية الشبكة العصبية ، سنقلل حجم الصورة إلى متجه تقديرات الفئة الموجودة على طول العمق (البعد الثالث).

التصور:

الشبكة العصبية القياسية	الشبكة العصبية التلافيفية

الجانب الأيسر: شبكة عصبية قياسية ثلاثية الطبقات.
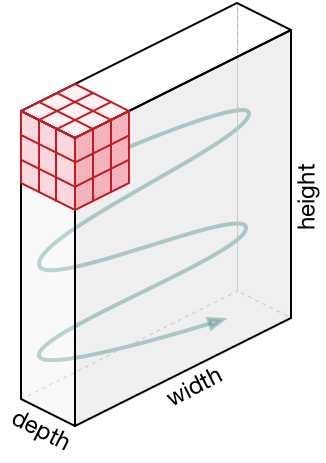
على الجانب الأيمن: تحتوي الشبكة العصبية التلافيفية على خلاياها العصبية في 3 أبعاد (العرض ، الارتفاع ، العمق) ، كما هو موضح في إحدى الطبقات. تقوم كل طبقة شبكة عصبية تلافيفية بتحويل تمثيل ثلاثي الأبعاد للمدخلات إلى تمثيل ثلاثي الأبعاد للمخرجات كخلايا تنشيط. في هذا المثال ، تحتوي طبقة الإدخال الحمراء على الصورة ، لذلك سيكون حجمها مساويًا لحجم الصورة ، وسيكون العمق 3 (ثلاث قنوات - الأحمر والأخضر والأزرق).

تتكون الشبكة العصبية التلافيفية من طبقات. كل طبقة عبارة عن واجهة برمجة تطبيقات بسيطة: تقوم بتحويل تمثيل الأبعاد الثلاثية إلى تمثيل ثلاثي الأبعاد للمخرجات لوظيفة مختلفة ، والتي قد تحتوي أو لا تحتوي على معلمات.

الطبقات المستخدمة لبناء شبكات عصبية تلافيفية

كما سبق أن ذكرنا أعلاه ، فإن الشبكة العصبية التلافيفية البسيطة عبارة عن مجموعة من الطبقات ، حيث تقوم كل طبقة بتحويل تمثيل إلى آخر باستخدام وظيفة مختلفة. نستخدم ثلاثة أنواع رئيسية من الطبقات لبناء شبكات عصبية تلافيفية: طبقة تلافيفية ، طبقة جزئية ، وطبقة متصلة بالكامل (نفس التي نستخدمها في شبكة عصبية عادية). نرتب هذه الطبقات بالتتابع للحصول على بنية SNA.

مثال العمارة: نظرة عامة. أدناه سنبحث في التفاصيل ، ولكن في الوقت الحالي ، بالنسبة لمجموعة بيانات CIFAR-10 ، قد تكون بنية شبكتنا العصبية التلافيفية [INPUT -> CONV -> RELU -> POOL -> FC] . الآن بمزيد من التفاصيل:

• سيحتوي INPUT [32x32x3] على القيم الأصلية لوحدات بكسل الصورة ، في حالتنا ، تكون الصورة بعرض 32 بكسل ، وارتفاع 32 بكسل و 3 قنوات ملونة R و G و B.
• ستنتج طبقة CONV مجموعة من الخلايا العصبية التي سيتم ربطها بالمنطقة المحلية لصورة مصدر الإدخال ؛ ستحسب كل خلية عصبية مثل هذا المنتج القياسي بين أوزانه والجزء الصغير من الصورة الأصلية الذي يرتبط به. يمكن أن تكون قيمة الإخراج عبارة عن تمثيل ثلاثي الأبعاد يبلغ 323212 ، على سبيل المثال ، إذا قررنا استخدام 12 فلترًا.
• RELU طبقة RELU وظيفة تنشيط العنصر max(0, x) . لن يغير هذا التحويل بعد البيانات - [32x32x12] .
• ستنفذ طبقة POOL عملية أخذ عينات من الصورة بعدين - الارتفاع والعرض ، مما يتيح لنا تمثيلًا ثلاثي الأبعاد جديدًا [161612] .
• FC طبقة FC (الطبقة المتصلة بالكامل) التقديرات حسب الفئات ، وسيكون البعد الناتج هو [1x1x10] ، حيث [1x1x10] كل من القيم العشرة مع درجات فئة معينة بين 10 فئات من الصور من CIFAR-10. كما هو الحال في الشبكات العصبية التقليدية ، سيتم ربط كل خلية عصبية من هذه الطبقة بجميع الخلايا العصبية في الطبقة السابقة (تمثيل ثلاثي الأبعاد).

هذه هي الطريقة التي تحول بها الشبكة العصبية التلافيفية الصورة الأصلية ، طبقة تلو الأخرى ، من قيمة البيكسل الأولية إلى تقدير الفصل النهائي. لاحظ أن بعض الطبقات تحتوي على خيارات ، وبعضها لا يحتوي على خيارات. على وجه الخصوص ، تقوم طبقات CONV/FC بتحويل ، وهي ليست وظيفة تعتمد فقط على بيانات الإدخال ، ولكنها تعتمد أيضًا على القيم الداخلية للأوزان والتشريد في الخلايا العصبية نفسها. طبقات RELU/POOL ، من ناحية أخرى ، تستخدم وظائف غير معلمة. سيتم تدريب المعلمات في طبقات CONV/FC بواسطة تدرج النسب بحيث يتلقى الإدخال تسميات الإخراج الصحيحة المقابلة.

لتلخيص:

• بنية الشبكة العصبية التلافيفية ، في أبسط تمثيل لها ، هي مجموعة مرتبة من الطبقات التي تحول تمثيل الصورة إلى تمثيل آخر ، على سبيل المثال ، تقديرات عضوية الفئة.
• هناك عدة أنواع مختلفة من الطبقات (CONV - الطبقة التلافيفية ، FC - متصلة بالكامل ، RELU - وظيفة التنشيط ، POOL - طبقة العينة الفرعية - الأكثر شيوعًا).
• تتلقى كل طبقة إدخال تمثيلًا ثلاثي الأبعاد وتحولها إلى تمثيل ثلاثي الأبعاد للمخرجات باستخدام وظيفة يمكن تمييزها.
• كل طبقة قد لا تحتوي على معلمات (CONV / FC - لها معلمات ، RELU / POOL - لا).
• كل طبقة قد لا تحتوي على معلمات مفرطة (CONV / FC / POOL - لها ، RELU - لا)

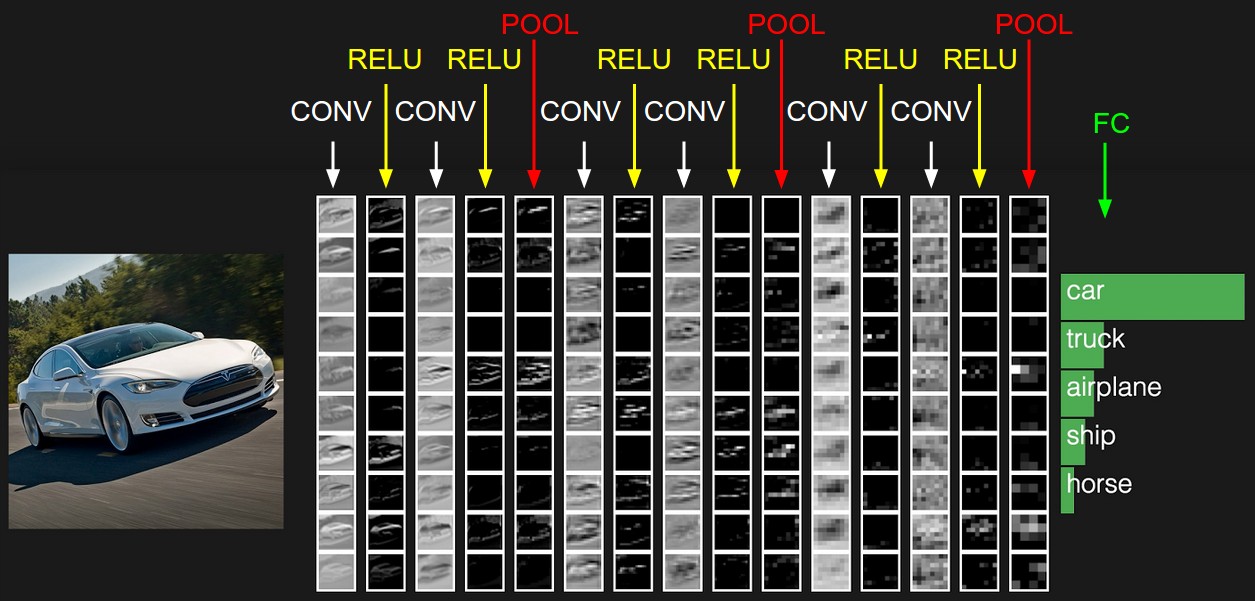
يحتوي التمثيل الأولي على قيم البكسل للصورة (على اليسار) وتقديرات للفئات التي ينتمي إليها الكائن في الصورة (على اليمين). يتم تمييز كل تحويل عرض كعمود.

طبقة تلافيفية

الطبقة التلافيفية هي الطبقة الرئيسية في بناء الشبكات العصبية التلافيفية.

نظرة عامة دون الغوص في ميزات الدماغ. دعونا نحاول أولاً معرفة ما الذي لا تزال تحسبه طبقة CONV دون الغمر واللمس في موضوع الدماغ والخلايا العصبية. تتكون معلمات الطبقة التلافيفية من مجموعة من المرشحات المدربة. كل مرشح عبارة عن شبكة صغيرة بطول العرض والارتفاع ، ولكنه يمتد عبر العمق الكامل لتمثيل الإدخال.

على سبيل المثال ، يمكن أن يكون للمرشح القياسي على الطبقة الأولى من الشبكة العصبية التلافيفية أبعاد 5 × 5 × 3 (5 بكسل - العرض والارتفاع ، 3 - عدد قنوات الألوان). أثناء تمرير مباشر ، ننتقل (على وجه الدقة - ننهار) المرشح على طول عرض وارتفاع تمثيل المدخلات وحساب المنتج القياسي بين قيم المرشح والقيم المقابلة لتمثيل المدخلات في أي نقطة. في عملية نقل المرشح على طول عرض وارتفاع تمثيل المدخلات ، نقوم بتكوين خريطة تنشيط ثنائية الأبعاد تحتوي على قيم تطبيق هذا المرشح على كل منطقة من مناطق تمثيل الإدخال. بشكل حدسي ، يصبح من الواضح أن الشبكة ستعلم المرشحات التنشيط عندما يرون علامة بصرية معينة ، على سبيل المثال ، خط مستقيم بزاوية معينة أو تمثيلات على شكل عجلة في مستويات أعلى. الآن بعد أن قمنا بتطبيق جميع عوامل التصفية لدينا على الصورة الأصلية ، على سبيل المثال ، كان هناك 12. نتيجة لتطبيق 12 مرشحًا ، تلقينا 12 بطاقة تنشيط من البعد 2. لإنتاج تمثيل إخراج ، نجمع هذه البطاقات (بالتتابع في البعد الثالث) ونحصل على تمثيل البعد [WxHx12].

لمحة عامة نربط بين الدماغ والخلايا العصبية. إذا كنت من محبي الدماغ والخلايا العصبية ، يمكنك أن تتخيل أن كل خلية عصبية "تنظر" إلى قسم كبير من تمثيل المدخلات وتنقل المعلومات حول هذا القسم إلى الخلايا العصبية المجاورة. سنناقش أدناه تفاصيل اتصال الخلايا العصبية وموقعها في الفضاء وآلية مشاركة المعلمات.

الاتصال المحلي. عندما نتعامل مع بيانات المدخلات بعدد كبير من الأبعاد ، على سبيل المثال ، كما في حالة الصور ، إذن ، كما رأينا بالفعل ، ليست هناك حاجة على الإطلاق لتوصيل الخلايا العصبية بجميع الخلايا العصبية في الطبقة السابقة. بدلاً من ذلك ، سنقوم بتوصيل الخلايا العصبية فقط بالمناطق المحلية لتمثيل المدخلات. الدرجة المكانية للاتصال هي واحدة من المعلمات المفرطة وتسمى حقل تقبلا (حقل تقبلا للخلايا العصبية هو حجم نفس مرشح / الالتواء الأساسية). درجة الاتصال على طول البعد الثالث (العمق) تساوي دائمًا عمق التمثيل الأصلي. من المهم للغاية التركيز على هذا مرة أخرى ، الانتباه إلى كيفية تعريف الأبعاد المكانية (العرض والارتفاع) والعمق: اتصالات الخلايا العصبية محلية في العرض والارتفاع ، ولكن تمتد دائمًا طوال العمق الكامل لتمثيل المدخلات.

مثال 1. تخيل أن حجم تمثيل المدخلات يبلغ 32 × 32 × 3 (RGB ، CIFAR-10). إذا كان حجم الفلتر (مجال تقبلا للخلية العصبية) هو 5 × 5 ، فإن كل خلية عصبية في الطبقة التلافيفية سيكون لها أوزان في المنطقة 5 × 5 × 3 من التمثيل الأصلي ، مما سيؤدي في النهاية إلى إنشاء روابط 5 × 5 × 3 = 75 (أوزان) + معلمة إزاحة واحدة. يرجى ملاحظة أن درجة الترابط في العمق يجب أن تساوي 3 ، لأن هذا هو بُعد التمثيل الأصلي.

مثال 2. تخيل أن حجم تمثيل المدخلات 16 × 16 × 20. باستخدام مثال على ذلك الحقل التقبيلي لخلية عصبية بحجم 3x3 ، سيكون لكل خلية عصبية طبقة تلافيفية 3x3x320 = 180 اتصال (أوزان) + معلمة إزاحة واحدة. لاحظ أن الاتصال محلي في العرض والارتفاع ، لكنه كامل في العمق (20).

# 1	# 2

من الجانب الأيسر: يتم عرض تمثيل المدخلات باللون الأحمر (على سبيل المثال ، صورة بحجم 32x332 CIFAR-10) ومثال على تمثيل الخلايا العصبية في الطبقة التلافيفية الأولى. ترتبط كل خلية عصبية في الطبقة التلافيفية فقط بالمنطقة المحلية لتمثيل المدخلات ، ولكن متعمقة تمامًا (في المثال ، على طول جميع قنوات الألوان). يرجى ملاحظة أن هناك الكثير من الخلايا العصبية في الصورة (في المثال - 5) وتقع على طول البعد الثالث (العمق) - سيتم تقديم توضيحات بشأن هذا الترتيب أدناه.
على الجانب الأيمن: لا تزال الخلايا العصبية من الشبكة العصبية دون تغيير: فهي لا تزال تحسب المنتج القياسي بين أوزانها وبيانات المدخلات ، وتطبق وظيفة التنشيط ، ولكن الاتصال بها محدود الآن بالمنطقة المحلية المكانية.

الموقع المكاني. لقد توصلنا بالفعل إلى اتصال كل خلية عصبية في الطبقة التلافيفية مع تمثيل المدخلات ، لكننا لم نناقش بعد عدد هذه الخلايا العصبية أو كيف توجد. تؤثر ثلاثة معلمات تشعبية على حجم عرض المخرجات: العمق والخطوة والمحاذاة .

1. يمثل عمق تمثيل الإخراج معلمة مفرطة: فهو يتوافق مع عدد المرشحات التي نريد تطبيقها ، ويتعلم كل منها شيئًا آخر في التمثيل الأصلي. على سبيل المثال ، إذا استقبلت الطبقة التلافيفية الأولى صورة كمدخل ، فيمكن تنشيط خلايا عصبية مختلفة على طول البعد الثالث (العمق) في وجود اتجاهات مختلفة للخطوط في منطقة معينة أو مجموعات من لون معين. مجموعة الخلايا العصبية التي "تنظر" في نفس المنطقة من تمثيل المدخلات ، وسوف نسمي العمود العميق (أو "الألياف" - الألياف).
2. نحتاج إلى تحديد الخطوة (حجم الإزاحة بالبكسل) التي سينتقل بها المرشح. إذا كانت الخطوة 1 ، فإننا نحول المرشح بمقدار 1 بكسل في تكرار واحد. إذا كانت الخطوة 2 (أو ، وهي أقل استخدامًا ، 3 أو أكثر) ، فإن الإزاحة تحدث لكل بكسلين في تكرار واحد. ينتج عن خطوة أكبر تمثيل إخراج أصغر.
3. كما سنرى قريبًا ، قد يكون من الضروري في بعض الأحيان استكمال تمثيل المدخلات على طول الحواف مع الأصفار. حجم المحاذاة (عدد الأعمدة / الصفوف المحشوة صفر) هو أيضًا معلمة مفرطة. تتمثل الميزة الرائعة لاستخدام المحاذاة في حقيقة أن المحاذاة سوف تتيح لنا التحكم في بعد تمثيل المخرجات (في أغلب الأحيان سنحتفظ بالأبعاد الأصلية للعرض - مع الحفاظ على عرض وارتفاع تمثيل المدخلات مع عرض وارتفاع تمثيل المخرجات).

يمكننا حساب البعد النهائي لتمثيل المخرجات من خلال تقديمه كدالة لحجم تمثيل المدخلات ( W ) ، وحجم الحقل الاستقبالي للخلايا العصبية من الطبقة التلافيفية ( F ) ، والخطوة ( S ) ، وحجم المحاذاة ( P ) على الحدود. يمكنك أن ترى بنفسك أن الصيغة الصحيحة لحساب عدد الخلايا العصبية في تمثيل الإخراج هي كما يلي (W - F + 2P) / S + 1 . على سبيل المثال ، للحصول على تمثيل مدخلات بحجم 7 × 7 وحجم مرشح 3 × 3 والخطوة 1 والمحاذاة 0 ، نحصل على تمثيل إخراج بحجم 5 × 5. في الخطوة 2 ، سنحصل على تمثيل إخراج 3 × 3. دعونا نلقي نظرة على مثال آخر ، هذه المرة موضحة بيانياً:

شكل توضيحي للترتيب المكاني. في هذا المثال ، لا يوجد سوى بُعد مكاني واحد (المحور السيني) ، وخلايا عصبية واحدة ذات مجال تقبلا F = 3 ، وحجم تمثيل المدخلات W = 5 والمحاذاة P = 1 . على الجانب الأيسر : يتحرك الحقل الاستقبالي للخلية العصبية بخطوة S = 1 ، والتي تعطي بالتالي حجم تمثيل المخرجات (5 - 3 + 2) / 1 + 1 = 5. على الجانب الأيمن : تستخدم الخلية العصبية حقل تقبلا للحجم S = 2 ، والذي في والنتيجة هي حجم تمثيل المخرجات (5 - 3 + 2) / 2 + 1 = 3. لاحظ أنه لا يمكن استخدام حجم الخطوة S = 3 ، لأنه مع حجم الخطوة هذا ، لن يلتقط الحقل التلقي جزءًا من الصورة. إذا استخدمنا صيغتنا ، فعندئذٍ (5 - 3 + 2) = 4 ليست مضاعفات 3. أوزان الخلايا العصبية في هذا المثال هي [1 ، 0 ، -1] (كما هو موضح في الصورة في أقصى اليمين) ، والإزاحة هي صفر. يتم مشاركة هذه الأوزان من قبل جميع الخلايا العصبية الصفراء.

باستخدام المحاذاة . انتبه إلى المثال الموجود على الجانب الأيسر ، والذي يحتوي على 5 عناصر في الإخراج و 5 عناصر في الإخراج. نجح هذا لأن حجم الحقل الاستقبالي (عامل التصفية) كان 3 واستخدمنا المحاذاة P = 1 . إذا لم يكن هناك محاذاة ، فإن حجم تمثيل المخرجات سيكون مساوياً لـ 3 ، لأنه كان بالضبط الكثير من الخلايا العصبية التي تناسب ذلك. بشكل عام ، يتيح لك ضبط حجم المحاذاة P = (F - 1) / 2 بخطوة مساوية لـ S = 1 الحصول على حجم تمثيل الإخراج المماثل لتمثيل الإدخال. غالبًا ما يتم تطبيق نهج مماثل باستخدام المحاذاة في الممارسة العملية ، وسوف نناقش الأسباب أدناه عندما نتحدث عن بنية الشبكات العصبية التلافيفية.

حدود حجم الخطوة . يرجى ملاحظة أن المعلمات المفرطة المسؤولة عن الترتيب المكاني ترتبط أيضًا بالقيود. على سبيل المثال ، إذا كان تمثيل الإدخال بحجم W = 10 ، P = 0 وحجم الحقل الاستقبالي F = 3 ، يصبح من المستحيل استخدام حجم خطوة يساوي S = 2 ، لأن (W - F + 2P) / S + 1 = (10 - 3 + 0) / 2 + 1 = 4.5 ، والذي يعطي قيمة عدد صحيح من الخلايا العصبية. وبالتالي ، فإن مثل هذا التكوين للمعلمات المفرطة يعتبر غير صالح ، وستلغي المكتبات للعمل مع الشبكات العصبية التلافيفية استثناء أو محاذاة للقوة أو حتى تقطع تمثيل المدخلات. كما سنرى في الأقسام التالية من هذا الفصل ، لا يزال تعريف المعلمات المفرطة للطبقة التلافيفية يمثل صداعًا يمكن تقليله باستخدام بعض التوصيات و "قواعد النغمة الجيدة" عند تصميم بنية الشبكات العصبية التلافيفية.

مثال الحياة الحقيقية . هندسة الشبكات العصبية التلافيفية Krizhevsky et al. ، التي فازت بمسابقة ImageNet في عام 2012 ، تلقت 227x227x3 صورة. في الطبقة التلافيفية الأولى ، استخدمت حقل تقبلا من الحجم F = 11 ، والخطوة S = 4 ، وحجم المحاذاة P = 0 . نظرًا لأن (227 - 11) / 4 + 1 = 55 ، وكانت الطبقة التلافيفية K = 96 بعمق ، كان البعد الناتج للعرض التقديمي 55x55x96. ارتبط كل من الخلايا العصبية 55x55x96 في هذا التمثيل مع منطقة بحجم 11x11x3 في تمثيل المدخلات. علاوة على ذلك ، ترتبط جميع الخلايا العصبية البالغ عددها 96 في العمود العميق بنفس منطقة 11x11x3 ، ولكن مع أوزان مختلفة. والآن قليلاً من الفكاهة - إذا قررت التعرف على المستند الأصلي (دراسة) ، فاحرص على أن المستند ينص على أن الإدخال يتلقى 224x24 صورة ، وهذا لا يمكن أن يكون صحيحًا ، لأن (224 - 11) / 4 + 1 بأي حال من الأحوال إعطاء قيمة عدد صحيح. غالبًا ما يتم الخلط بين هذا النوع من الحالات بالنسبة للأشخاص في القصص والشبكات العصبية التلافيفية. أظن أن Alex استخدم حجم المحاذاة P = 3 ، لكن نسيت أن أذكر ذلك في المستند.

خيارات المشاركة. يتم استخدام آلية مشاركة المعلمات في الطبقات التلافيفية للتحكم في عدد المعلمات. انتبه إلى المثال أعلاه ، حيث يمكنك أن ترى أن هناك 55x55x96 = 290400 خلية على الطبقة التلافيفية الأولى ولكل من العصبونات 11 × 11 × 3 = 363 أوزان + قيمة إزاحة واحدة. في المجموع ، إذا ضاعفنا هاتين القيمتين ، فسنحصل على 290400x364 = 105 705 600 معلمة فقط على الطبقة الأولى من الشبكة العصبية التلافيفية. من الواضح أن هذا له أهمية كبيرة!

اتضح أنه من الممكن تقليل عدد المعلمات بشكل كبير عن طريق القيام بافتراض واحد: إذا كانت بعض الخصائص المحسوبة في الموضع (س ، ص) تهمنا ، فستكون هذه الخاصية المحسوبة في الموضع (x2 ، ص 2) مهمة لنا أيضًا. وبعبارة أخرى ، عند الإشارة إلى "الطبقة" ثنائية الأبعاد بعمق باعتبارها "طبقة عميقة" (على سبيل المثال ، تحتوي طريقة العرض [55x55x96] على 96 طبقة عميقة ، كل منها بحجم 55 × 55) ، سنقوم ببناء الخلايا العصبية بعمق بنفس الأوزان والإزاحة. باستخدام مخطط مشاركة المعلمات ، ستحتوي الآن الطبقة التلافيفية الأولى في مثالنا على 96 مجموعة فريدة من الأوزان (كل مجموعة لكل طبقة عمق) ، في المجموع سيكون هناك 96 × 11 × 11 × 3 = 34،848 أوزان فريدة أو 34،944 معلمة (+ 96 إزاحة). بالإضافة إلى ذلك ، فإن جميع الخلايا العصبية 55 × 55 في كل طبقة عميقة تستخدم الآن نفس المعلمات. في الممارسة العملية ، أثناء الانتشار الخلفي ، ستحسب كل خلية عصبية في هذا التمثيل التدرج للأوزان الخاصة بها ، ولكن سيتم تلخيص هذه التدرجات على كل طبقة عمق وتحديث مجموعة واحدة فقط من الأوزان في كل مستوى.

لاحظ أنه إذا استخدمت جميع الخلايا العصبية في نفس الطبقة العميقة نفس الأوزان ، ثم للانتشار المباشر من خلال الطبقة التلافيفية ، سيتم حساب الإلتواء بين قيم أوزان الخلايا العصبية وبيانات الإدخال. هذا هو السبب في أنه من المعتاد استدعاء مجموعة واحدة من الأوزان - مرشح (الأساسية) .

أمثلة على المرشحات التي تم الحصول عليها عن طريق تدريب النموذج Krizhevsky et al. يبلغ حجم كل مرشح من 96 مرشحًا معروضًا هنا 11 × 11 × 3 ، ويتم مشاركة كل منها بواسطة جميع الخلايا العصبية 55 × 55 من طبقة عميقة واحدة. يرجى ملاحظة أن افتراض مشاركة نفس الأوزان أمر منطقي: إذا كان اكتشاف الخط الأفقي مهمًا في أحد أجزاء الصورة ، فمن الواضح بشكل حدسي أن هذا الكشف مهم في جزء آخر من هذه الصورة. لذلك ، لا معنى لإعادة التدريب في كل مرة للعثور على خطوط أفقية في كل مكان من 55x55 أماكن مختلفة من الصورة في الطبقة التلافيفية.

يجب أن يؤخذ في الاعتبار أن افتراض معلمات المشاركة قد لا يكون دائمًا منطقيًا. على سبيل المثال ، إذا تم تغذية صورة ذات بنية مركزية بإدخال شبكة عصبية تلافيفية ، حيث نود أن نكون قادرين على تعلم خاصية في جزء واحد من الصورة وممتلكات أخرى في الجزء الآخر من الصورة. مثال عملي هو الصور ذات الوجه المركزي. يمكن افتراض أنه يمكن تحديد علامات مختلفة للعين أو الشعر في مناطق مختلفة من الصورة ، وبالتالي ، في هذه الحالة ، يتم استخدام استرخاء الأوزان وتسمى الطبقة متصلة محليًا .

أمثلة شاذة . يجب أن يتم نقل المناقشات السابقة إلى مستوى التفاصيل وعلى أمثلة مع الكود. تخيل تمثيل المدخلات عبارة عن مجموعة numpy من X ثم:

• سيتم تمثيل العمود العميق ( سلسلة ) في الموضع (x,y) على النحو التالي X[x,y,:] .
• الطبقة العميقة ، أو كما أطلقنا سابقًا على هذه الطبقة - خريطة التنشيط في العمق d سيتم تمثيلها على النحو التالي X[:,:,d] .

مثال على طبقة تلافيفية . , X X.shape: (11,11,4) . , P=1 , () F=5 S=1 . 44, — (11-5)/2+1=4. ( V ), ( ):

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

, numpy , * . , W0 b0 . W0 W0.shape: (5,5,4) , 5, 4. . , , 2 ( ). :

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (, y )
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (, )

— W1 b1 . , V . , , , ReLU , . .

. :

• W1 x H1 x D1
• 4 -:
  
  • K ,
  • F ,
  • S ,
  • P .
• W2 x H2 x D2 ,
  
  • W2 = (W1 — F + 2P)/S + 1
  • H2 = (H1 — F + 2P)/S + 1
  • D2 = K
• F x F x D1 , (F x F x D1) x K K .
• , d - ( W2 x H2 ) d - S d -.

- F = 3, S = 1, P = 1 . . " ".

. . 3D- ( — , — , — ), — . W1 = 5, H1 = 5, D1 = 3 , K = 2, F = 3, S = 2, P = 1 . , 33, 2. (5 — 3 + 2)/2 + 1 = 3. , , P = 1 . , () , .

( , html+css , )

. (). :

1. im2col . , 227x227x3 11113 4, 11113 = 363 . , 4 , (227 — 11) / 4 + 1 = 55 , X_col 3633025, 3025. , , , (), .
2. . , 96 11113, W_row 96363.
3. — np.dot(W_row, X_col) , . 963025.
4. 555596.

, , — , . , , — (, BLAS API). , im2col , .

. ( ) ( , ) ( - ). , .

11 . 11, Network in Network . , 11, , . , 2- , 11 ( ). , , 3- , . , 32323, 11, , , 3 (R, G, B — , ).

. - . . , . w 3 x : w[0] x[0] + w[1] x[1] + w[2] x[2] . 0. 1 : w[0] x[0] + w[1] x[2] + w[2] x[4] . "" 1 . , . , 2 33, , 55 ( 55 ). .

— . , , . , MAX. 22 2, 2 , 75% . MAX 22. . , :

• W1 x H1 x D1
• 2 -:
  
  • F ,
  • S ,
• W2 x H2 x D2 , :
  
  • W2 = (W1 — F)/S + 1
  • H2 = (H1 — F)/S + 1
  • D2 = D1
• ,
• (zero-padding ).

, : F=3, S=2 ( ), — F=2, S=2 . - .

. , , , L2-. , , .

#1	#2

. : 22422464 22 2, 11211264. , . : — (max-pooling), 2. 4 ( 22)

. , max(a,b) — . , ( ), .

. , . , : , . . , (VAEs) (GANs). , - , .

, , . , , . .

, . .

, , ( ). - , . , :

• , . , , , , , .
• , . , K=4096 ( ), 7712 - F=7, P=0, S=1, K=4096 . , 114096, .

. , . , 2242243 77512 ( AlexNet, , 5 , 7 — 224/2/2/2/2/2 = 7). AlexNet 4096 , , 1000 , . :

• , "" 77512, F=7 , 114096.
• F=1 , 114096.
• F=1 , 111000.

, , ( ) W . , "" () .

, 224224 , 77512 — 32 , 384384 1212512, 384/32 = 12. , , , 661000, (12 — 7)/1 + 1 = 6. , 111000 66 384384 .

( ) 384384, 224244 32 , , .

, , 36 , 36 . , , . .

, , 32 ? ( ). , 16 , 2 : 16 .

, , 3 : , ( , ) . ReLU , - . .

CONV-RELU-, POOL- , . - . , , . , :

 INPUT -> [[CONV -> RELU]*N -> POOL?] * M -> [FC -> RELU]*K -> FC 

* , POOL? . , N >= 0 ( N <= 3 ), M >= 0 , K >= 0 ( K < 3 ). , , :

• INPUT -> FC , . N = M = K = 0 .
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC , .
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC . 2 . , , .

. 3 33 ( RELU , ). "" 33 . "" 33 , — 55. "" 33 , — 77. , 33 77. "" 77 ( ) , . -, , 3 , . -, C , , 77 (C(77)) = 49xxC , 33 3((33)) = 27 . , , . — , .

. , , Google, Microsoft. .

: , ImageNet. , , 90% . — " ": , , , ImageNet — , . .

-, . , :

( ) 2 . 32 (, CIFAR-10), 64, 96 (, STL-10), 224 (, ImageNet), 384 512.

(, 33 , 55), S=1 , , , . , F=3 P=1 . F=5, P=2 . F , P=(F-1)/2 . - ( 77), .

. 22 ( F=2 ) 2 ( S=2 ). , 75% (- , ). , , 33 ( ) 2 ( ). 33 , . .

. , , . , 1 , , .

1 ? . , 1 ( ), .

? , . , , , .

. ( ), , . , 64 33 1 2242243, 22422464. , , 10 , 72 ( , ). GPU, . , 77 2. , AlexNet, 1111 4.

. :

• LeNet . Yann LeCun 1990. LeNet , ZIP-, .
• AlexNet . , , Alex Krizhevsky, Ilya Sutskever Geoff Hinton. AlexNet ImageNet ILSVRC 2012 ( : 16% 26%). LeNet, , ( ).
• ZFNet . ILSVRC 2013 Matthew Zeiler Rob Fergus. ZFNet. AlexNet, -, .
• GoogLeNet . ILSVRC 2014 Szegedy et al. Google. Inception-, (4 60 AlexNet). , , . , — Inveption-v4.
• VGGNet . 2014 ILSVRC Karen Simonyan Andrew Zisserman, VGGNet. , . 16 + (33 22 ). . VGGNet — (140). , , , .
• ResNet . Residual- Kaiming He et al. ILSVRC 2015. . . ( 2016).

VGGNet . VGGNet . VGGNet , 33, 1 1, 22 2. ( ) :

 INPUT: [224x224x3] memory: 224*224*3=150K weights: 0 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864 POOL2: [112x112x64] memory: 112*112*64=800K weights: 0 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456 POOL2: [56x56x128] memory: 56*56*128=400K weights: 0 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 POOL2: [28x28x256] memory: 28*28*256=200K weights: 0 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 POOL2: [14x14x512] memory: 14*14*512=100K weights: 0 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 POOL2: [7x7x512] memory: 7*7*512=25K weights: 0 FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448 FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216 FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000 TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd) TOTAL params: 138M parameters 

, , ( ) , . 100 140 .

. GPU 3/4/6 , GPU — 12 . , :

• : , ( ). , . , .
• : , , . , , 3 .
• , , ..

(, ), . , 4 ( 4 , — 8), 1024 , , . " ", , .

… call-to-action — , share :)
يوتيوب
برقية
فكونتاكتي