🤙🏽 😑 🆚 لوجستيات العمل من أجل مجموعة منفصلة من المواد القابلة لإعادة التدوير 🛌 🃏 ☝🏽

بدلا من الانضمام

عندما يتم ضبط عمليات جمع النفايات ومعالجتها بالكامل في روسيا ، ليس من السهل القول ، لكنني لا أريد المشاركة في تجديد مدافن النفايات الآن. لذلك ، في العديد من المدن الكبيرة ، بطريقة أو بأخرى ، هناك حركات تطوعية تشارك في مجموعة منفصلة خاصة.

في نوفوسيبيرسك ، يتم تشكيل مثل هذا النشاط حول حملة السنجاب الخضراء ، حيث يقوم سكان البيئة مرة كل شهر بإحضار النفايات المنزلية المتراكمة القابلة لإعادة التدوير إلى أماكن محددة مسبقًا في وقت معين. في الوقت نفسه ، تصل شاحنة مستأجرة إلى هناك ، والتي تنقل المواد القابلة لإعادة التدوير التي تم جمعها وفرزها إلى الموقع ، حيث يتم إعادة توزيعها بين مختلف مؤسسات المعالجة. كان الإجراء موجودًا منذ عام 2014 ، ومنذ ذلك الحين زاد عدد نقاط تجميع المواد القابلة لإعادة التدوير وكذلك أحجامها زيادة كبيرة. بالنسبة لتوجيه الشاحنات ، لم تكن مجرد النظرة كافية ، وبدأنا في تطوير نماذج التحسين لتقليل تكاليف النقل. أول هذه النماذج هو موضوع هذه المقالة.

في القسم 1 ، سأصف بالتفصيل ومع الرسوم التوضيحية مخطط تنظيم العمل. علاوة على ذلك ، في القسم 2 ، سيتم إضفاء الطابع الرسمي على مهمة تقليل تكاليف النقل باعتبارها مهمة توجيه مشكلة توجيه المركبات غير المتجانسة في أسطول المركبات مع النوافذ الزمنية. تم تخصيص القسم 3 لحل هذه المشكلة باستخدام حزمة موزعة مجانًا لحل مشاكل البرمجة الرياضية الخطية الصحيحة المختلطة GLPK.

1. عمل "السنجاب الأخضر"

منذ عام 2014 ، تقوم مجموعة مبادرة Living Earth بحملة شهرية لفصل مجموعة السنجاب الأخضر المعاد تدويره في نوفوسيبيرسك. في وقت كتابة هذا التقرير ، يتم قبول إعادة التدوير مع عدد من التحفظات على نفايات بلاستيكية تحمل علامات PET و PE و PP و PS والزجاج والألمنيوم والحديد والأجهزة المنزلية ونفايات الورق وغير ذلك الكثير. يشارك أكثر من 50 متطوعًا في إعداد وإجراء العمل. الإجراء ليس تجاريًا ، والمشاركة فيه مجانية ولا تعني مكافأة مالية.

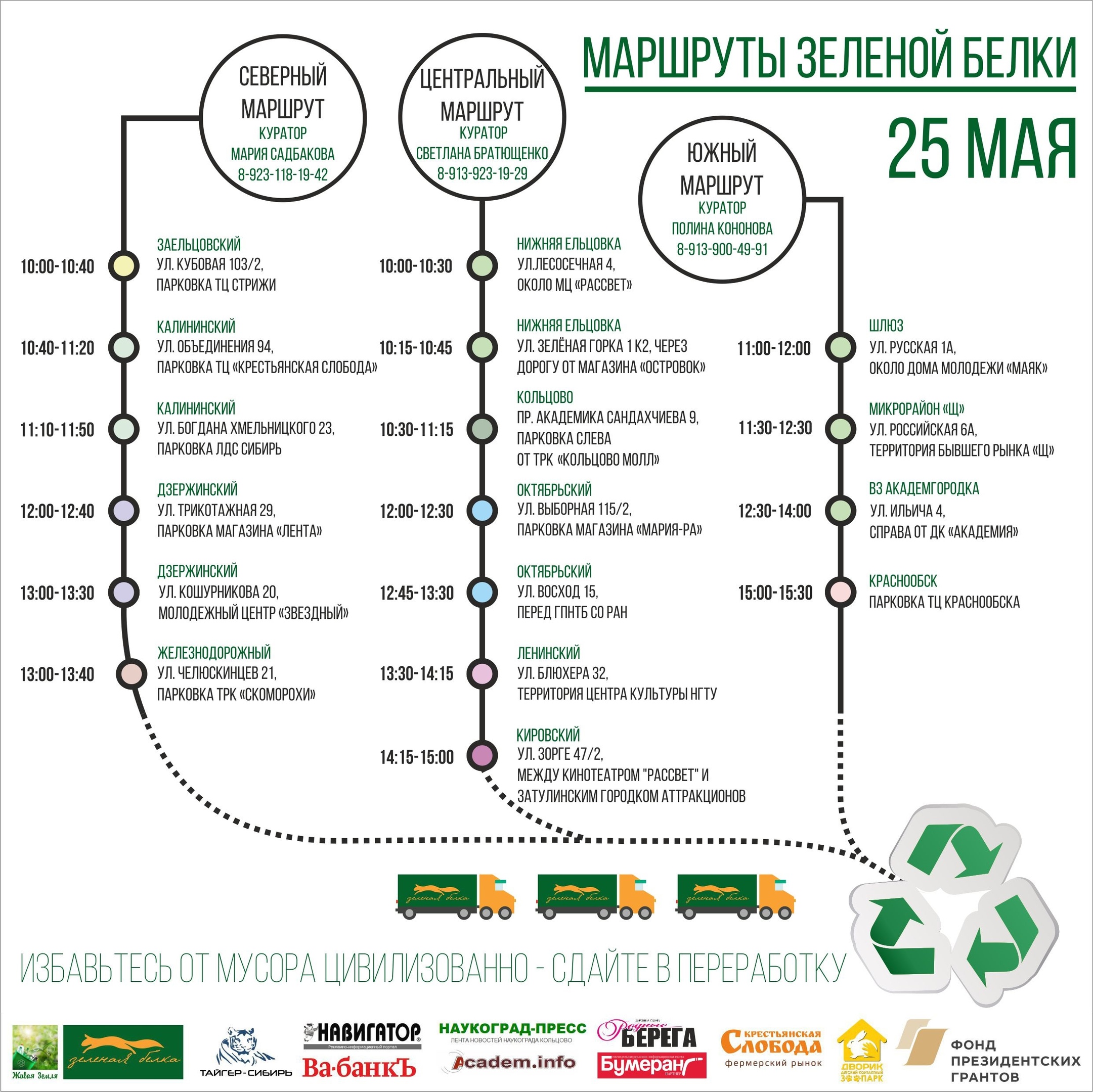
نقاط

يقام الحدث في 17 نقطة من المدينة ، وتقع من بعضها البعض على مسافات تغطيها السيارة في فترة من 15 إلى 90 دقيقة. واحدة من هذه النقاط في الصورة: أكياس على اليسار على طول الجدار لجمع كسور مختلفة من البلاستيك ، على اليمين - شاحنة ، يتم تحميل كل شيء في المستقبل ، وفي الوسط - متطوع بأذنين.

يتم تنظيم جميع الأنشطة في هذه المرحلة من قبل القيمين الذين لديهم قيود على الوقت الذي هم فيه على استعداد لأداء واجباتهم. عند التخطيط لإحدى الإجراءات ، يقوم القيمون بالإبلاغ عن الفاصل الزمني الذي يجب أن يمر الإجراء خلاله.

هناك أيضًا بيانات عن متوسط أحجام المواد القابلة لإعادة التدوير التي تم جمعها في كل نقطة.

طرق

يتم تنظيم النقاط في طرق يتم تشغيلها على التوالي بواسطة شاحنة. تتم مراقبة حركات الشاحنات بواسطة مشرفين على الطرق يقومون بمراقبة البيئة التشغيلية واتخاذ القرارات بشأن التعامل مع الأحداث الخاصة.

الشاحنات

يتم تأجيرها على أساس مشترك في إطار مقترحات لتأجير كل ساعة من مركبات الشحن. لا يمكن ضغط البلاستيك في مكانه ، وبالتالي فإن المعلمة الرئيسية التي تميز الشاحنة هي حجم الجسم. حمل القدرة في حالتنا ليست عاملا مقيدا.

ترتبط المصروفات الرئيسية للعمل بدفع إيجار الشاحنة ، وبالتالي فإن تخفيضها أمر حاسم لوجود وتطوير حصتنا ، التي تكتسب أهمية مؤسسية بمعنى تكوين أفكار حول الاستهلاك المسؤول. بعد ذلك ، سيتم وصف نهج لحل هذه المشكلة ، استنادًا إلى تطبيق أساليب التحسين المنفصلة ، أي البرمجة الرياضية.

2. إضفاء الطابع الرسمي

في بناء النموذج الرياضي ، سنبقى في إطار برامج خطية مختلطة عدد صحيح ، والتي فهم معرفة الجبر الفئة 7 كافية.

يمكن أن تترافق الصعوبة الوحيدة مع استخدام الرموز التجريدية وعلامات الجمع في الصيغ. آمل أن لا يخيف هذا القراء الذين لديهم لقاءات نادرة مع النصوص الرياضية.

في نموذج التحسين ، يمكن تمييز أربعة مكونات:

تشكيل مجموعات من النقاط التي تشكل طريقا منفصلا ؛
تحديد مخطط التفاف لكل مجموعة من المجموعات ؛
تلبية متطلبات وقت وصول الشاحنة في كل نقطة ؛
تحديد نوع الشاحنة اللازمة لخدمة كل من الطرق.

نحن نعتبر كل جزء من الأجزاء ، ونقدم الترميز اللازم عند الضرورة.

نقطة التجمع

سمح

V = \ {1 ، \ dots ، n \}

$V = \ {1 ، \ dots ، n \}$ هناك العديد من فهارس نقاط تجميع المواد القابلة لإعادة التدوير ، والموقع الذي يتم فيه نقل المواد القابلة للتدوير التي تم جمعها - وسنسميها المستودع - مؤشرًا يساوي 0. ضع

\ bar {V} = V \ cup \ {0 \}

$\ bar {V} = V \ cup \ {0 \}$

كل مجموعة من النقاط تشكل مسار منفصل. من خلال

R

$R$ تدل على مجموعة من أرقام الطريق.

دع الكمية

z_{i r} ، i i n I ، r i n R

$z_ {ir} ، i \ in I ، r \ in R$ يساوي واحد إذا كانت النقطة

i

$i$ المدرجة في الطريق مع الرقم

ص

$ص$ ، والصفر خلاف ذلك. ثم الشرط أن هذه النقطة

i i n V

$i \ in V$ يجب إدخال أحد الطرق التي يمكن كتابتها كـ

s u m_{r i n R} z_{i r} = z_{i 1} + z_{i 2} + d o t s + z_{i n} = 1.

$\ sum_ {r \ in R} z_ {ir} = z_ {i1} + z_ {i2} + \ dots + z_ {in} = 1.$

يجب أن يدخل المستودع في جميع المسارات:

z_{0 r} = 1 ، r i n R

$z_ {0r} = 1 ، r \ in R$

جماليات

لسوء الحظ ، فإن هذا السجل يخلق مشاكل حسابية مرتبطة بتناظر المنطقة المقبولة. يمكن إزالته عن طريق إضافة عدد من القيود لضمان اختيار التحلل المعجمي الأدنى. يمكنك قراءة المزيد عن هذا باللغة الروسية ، على سبيل المثال ، هنا .

1 - z_{i r} l e q s u m_{j = 1}^{i - 1} l e f t (1 - s u m_{k = 1}^{r - 1} z_{j k} r i g h t) + s u m_{k = 1}^{r - 1} z_{i k} ، q u a d i i n I ، r i n R ، r l e q i .

$1-z_ {ir} \ leq \ sum_ {j = 1} ^ {i-1} \ left (1- \ sum_ {k = 1} ^ {r-1} z_ {jk} \ right) + \ sum_ { k = 1} ^ {r-1} z_ {ik} ، \ quad i \ in I ، r \ in R ، r \ leq i.$

تعريف التفاف

الطرق هي سلسلة متتالية من النقاط والمقاطع بينهما. رسميا ، كلهم يبدأون في واحدة من نقاط المجموعة

V

$V$ ونهاية في المستودع ، ومع ذلك ، سيكون من الأسهل افتراض أن جميع المسارات دورية. هذا الافتراض لا يغير الجوهر ، لكنه يجعل كل القمم متساوية: في هذه الحالة لا توجد رؤوس نهاية ، كلها عبور.

للحصول على نقاط

i ، j i n b a r V

$i ، j \ in \ bar {V}$ والطريق

r i n R

$r \ in R$ إعداد متغير

x_{i j r}

$x_ {ijr}$ يساوي واحد إذا كان في الطريق مع عدد

ص

$ص$ شاحنة تتحرك من نقطة

i

$i$ الى هذه النقطة

j

$j$ ، والصفر خلاف ذلك.

ثم نطلب ، أولاً ، أن تتحرك الشاحنة على طول الطريق

r i n R

$r \ in R$ زار هذه النقطة

i i n V

$i \ in V$ إذا كانت ، بعد تقسيمها إلى مجموعات ، سقطت في المجموعة مع الرقم

ص

$ص$ :

s u m_{j i n b a r V} x_{j i r} = z_{i r} ، q u a d i i n b a r V ، r i n R .

$\ sum_ {j \ in \ bar {V}} x_ {jir} = z_ {ir} ، \ quad i \ in \ bar {V} ، r \ in R.$

ثانيا ، الشاحنة بعد وصولها إلى النقطة

i i n b a r V

$i \ in \ bar {V}$ يجب أن تتركها.

s u m_{j i n b a r V} x_{j i r} = s u m_{j i n b a r V} x_{i j r} ، q u a d i i n b a r V ، r i n R .

$\ sum_ {j \ in \ bar {V}} x_ {jir} = \ sum_ {j \ in \ bar {V}} x_ {ijr} ، \ quad i \ in \ bar {V} ، r \ in R .$

قد تلاحظ أن هذه القيود تسمح بالكميات

x_{i j r}

$x_ {ijr}$ تحديد الطرق التي هي عبارة عن مجموعة من حلقات disjoint. الطرق من هذا النوع ، بطبيعة الحال ، لا معنى لها ، وهناك عدد من القيود المطلوبة لتجنب ذلك.

حول القضاء على الدراجات النارية

يمكن أن تكون إحدى الطرق إدخال كميات غير سالبة مساعدة

f_{i j r} ، i ، j i n b a r V ، r i n R

$f_ {ijr} ، i ، j \ in \ bar {V} ، r \ in R$ تعمل مجموعة العلاقات المسجلة باستخدام هذه الكميات على إزالة مجموعات القيم

x_{i j r}

$x_ {ijr}$ تحديد الطرق التي ليست حلقة متصلة.

s u m_{i i n V} f_{0 j r} = s u m_{i i n V} z_{i r} ، q u a d r i n R ،

$\ sum_ {i \ in V} f_ {0jr} = \ sum_ {i \ in V} z_ {ir} ، \ quad r \ in R ،$

f_{i j r} l e q n x_{i j r} ، q u a d i i n b a r V ، j i n b a r V ، r i n R ،

$f_ {ijr} \ leq nx_ {ijr} ، \ quad i \ in \ bar {V} ، j \ in \ bar {V} ، r \ in R ،$

s u m_{j i n b a r V} f_{j i r} = s u m_{j i n b a r V} f_{i j r} + z_{i r} ، q u a d i i n V ، r i n ر و ب ي

$\ sum_ {j \ in \ bar {V}} f_ {jir} = \ sum_ {j \ in \ bar {V}} f_ {ijr} + z_ {ir} ، \ quad i \ in V ، r \ in روبي$

تحدد هذه النسب التدفق من المستودع إلى بقية نقاط المسار. في كل نقطة وسيطة ، يتم امتصاص وحدة التدفق ، لذلك من أجل أن يكون للشبكة تدفق طاقة يساوي عدد النقاط ناقص نقطة واحدة ، من الضروري توصيل المسار.

تلبية الاحتياجات في وقت وصول الشاحنة في كل نقطة

بمعنى آخر ، يجب عليك زيارة النقاط فقط داخل النوافذ الزمنية التي أشار إليها القيمون. من خلال

B_{i}

$B_i$ و

E_{i}

$E_i$ دلالة ، على التوالي ، على بداية ونهاية الفاصل الزمني الذي أمينة هذه النقطة

i

$i$ قد يحضره.

لتتبع تنفيذ هذه القيود ، نحتاج إلى معلومات حول الوقت الذي تقضيه الشاحنة أثناء التوقفات والمعابر على الطريق. من خلال

L_{i} ، i i n V

$L_i ، i \ in V$ تشير إلى مدة التحميل في هذه النقطة

i

$i$ و من خلال

D_{i j} ، i ، j i n b a r V

$D_ {ij} ، i ، j \ in \ bar {V}$ - وقت الانتقال من نقطة

i

$i$ الى هذه النقطة

j

$j$ نحن نبدي تحفظا

D_{0 i} = 0

$D_ {0i} = 0$ للجميع

i i n b a r V

$i \ in \ bar {V}$ ، وعموما يمكن أن يؤديها

D_{i j} n e q D_{j i}

$D_ {ij} \ neq D_ {ji}$ لأي

i n e q j

$i \ neq j$

نقدم متغيرات غير سلبية

a_{i} ، i i n b a r V

$a_i ، i \ in \ bar {V}$ و

w_{i r} ، i i n b a r V ، r i n R

$w_ {ir} ، i \ in \ bar {V} ، r \ in R$ يساوي أوقات الوصول وأوقات الانتظار في هذه النقطة

i

$i$ عند القيادة على طول الطريق

ص

$ص$ ، على التوالي. بالنسبة للقيم التي تم إدخالها ، يجب استيفاء العلاقات التالية.

لا يمكن أن يكون وقت الانتظار أقل من الوقت المطلوب للتحميل

w_{i r} g e q L_{i} z_{i r} ، q u a d i i n b a r V ، r i n R ،

$w_ {ir} \ geq L_iz_ {ir} ، \ quad i \ in \ bar {V} ، r \ in R ،$

ويساوي الصفر إذا كانت النقطة لا تنتمي إلى الطريق

ص

$ص$

w_{i r} l e q M z_{i r} ، q u a d i i n b a r V ، r i n R ،

$w_ {ir} \ leq Mz_ {ir} ، \ quad i \ in \ bar {V} ، r \ in R ،$

وقت الوصول في هذه النقطة

j

$j$ تحسب في الأوقات المناسبة للنقطة السابقة

i

$i$ هنا ثابت كبير إلى حد ما

M

$M$ تستخدم للقضاء على التبعيات غير الضرورية عند الانتقال بين

i

$i$ و

j

$j$ لم تفعل.

a_{i} + s u m_{r i n R} w_{i r} + D_{i j} l e q a_{j} + M (1 - s u m_{r i n R} x_{i j r}) ، q u a d i i n I ، j ف ي ا ل خ ا م س ،

$a_i + \ sum_ {r \ in R} w_ {ir} + D_ {ij} \ leq a_j + M (1 - \ sum_ {r \ in R} x_ {ijr}) ، \ quad i \ in I ، j \ في الخامس ،$

يجب أن يكون وصول ومغادرة الشاحنة ضمن الفاصل الزمني الذي يحدده المنسق.

a_{i} g e q B_{i} ، q u a d i i n V ،

$a_i \ geq B_i ، \ quad i \ in V ،$

a_{i} + s u m_{r i n R} w_{i r} l e q E_{i} ، q u a d i i n V .

$a_i + \ sum_ {r \ in R} w_ {ir} \ leq E_i ، \ quad i \ in V.$

تحديد نوع الشاحنة اللازمة لخدمة كل مسار
تشير إلى أنواع كثيرة من الشاحنات المتاحة للإيجار من قبل

T

$T$ نوع الشاحنة

t i n T

$t \ in T$ تتميز بحجم الجسم

C_{t}

$C_t$ وتكلفة إيجار ساعة واحدة

P_{t}

$P_t$ الحد الأدنى للوقت استئجار شاحنة

t

$t$ دلالة بواسطة

U_{t}^{0}

$U_t ^ 0$ كمية المواد القابلة للتدوير التي تم جمعها في هذه النقطة

i i n V

$i \ in V$ دلالة بواسطة

G_{i}

$G_i$

نحن نقدم المتغيرات

y_{t r} ، t i n T ، r i n R

$y_ {tr} ، t \ in T ، r \ in R$ يساوي واحد إذا كان نوع الشاحنة

t

$t$ المخصصة لطريق الخدمة مع عدد

ص

$ص$ ، والصفر خلاف ذلك.

متغيرات عدد صحيح

u_{t r} ، t i n T ، r i n R

$u_ {tr}، t \ in T، r \ in R$ ضبط وقت استئجار نوع الشاحنة

t

$t$ خدمة الطريق مع عدد

ص

$ص$
لكل طريق ،

r i n R

$r \ in R$ ، يجب عليك تعيين نوع الشاحنة:

s u m_{t i n T} y_{t r} = 1 ، q u a d r i n R

$\ sum_ {t \ in T} y_ {tr} = 1 ، \ quad r \ in R$

وفقًا لتفصيل النقاط بين المسارات ، قد تتحول بعض الطرق إلى تافهة ، أي أنها تحتوي على مستودعات فقط. إذا كان الطريق

ص

$ص$ غير تافهة ، ثم يتم استئجار الشاحنة المخصصة لها على الأقل

U_{t}^{0}

$U_t ^ 0$ ساعات.

u_{t r} g e q U_{t}^{0} (y_{t r} - s u m_{i i n V} z_{i r}) ، q u a d t i n T ، r i n R .

$u_ {tr} \ geq U_t ^ 0 (y_ {tr} - \ sum_ {i \ in V} z_ {ir}) ، \ quad t \ in T ، r \ in R.$

في الوقت نفسه ، يجب أن تتجاوز مدة عقد الإيجار أيضًا المدة الإجمالية لوقوف السيارات والتحرك على طول الطريق.

u_{t r} g e q s u m_{i i n V} s u m_{j i n b a r V} D_{i j} x_{i j r} + s u m_{i i n b a r V} w_{i r} - M (1 - y_{t r}) ، q u a d r i n R ، t i n T .

$u_ {tr} \ geq \ sum_ {i \ in V} \ sum_ {j \ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ in \ bar {V}} w_ { ir} -M (1-y_ {tr}) ، \ quad r \ in R ، t \ in T.$

أضف قيودًا توفر العقار: إذا كانت الشاحنة من النوع

t

$t$ لم يتم تعيينه إلى الطريق

ص

$ص$ ، وقت تأجيرها هو صفر.

u_{t r} l e q M y_{t r} .

$u_ {tr} \ leq My_ {tr}.$

جميع المواد القابلة لإعادة التدوير التي يتم جمعها في نقاط الطريق يجب أن تكون في الجزء الخلفي من الشاحنة.

s u m_{i i n V} G_{i} z_{i r} l e q s u m_{t i n T} C_{t} y_{t r} ، q u a d r i n R .

$\ sum_ {i \ in V} G_iz_ {ir} \ leq \ sum_ {t \ in T} C_ty_ {tr}، \ quad r \ in R.$

أخيرًا ، هدفنا هو تقليل تكلفة استئجار الشاحنات ، والتي تتم كتابتها باستخدام التسميات المقدمة

s u m_{t i n T} s u m_{r i n R} P_{t} u_{t r}

$\ sum_ {t \ in T} \ sum_ {r \ in R} P_tu_ {tr}$

ابحث عن حل

من السهل التحقق من أن جميع التعبيرات المتضمنة في نموذج التحسين هي وظائف خطية للمتغيرات ، وبالتالي ، للعثور على الحلول الدقيقة والتقريبية ، يمكنك استخدام حزم قياسية لحل مشاكل البرمجة المختلطة الصحيحة مثل Gurobi و CPLEX و Xpress و ORtools ، SCIP ، BLIS ، إلخ.
نكتب نموذجًا لتقليل تكاليف النقل بلغة GMPL. سيتيح لنا ذلك استخدام حزمة GLPK المجانية لأغراضنا . لكتابة التعليمات البرمجية وتصحيح النموذج ، سيكون من المناسب تنزيل بيئة تطوير GUSEK ، التي تحتوي بالفعل على GLPK في تكوينها.

يبدو GUSEK كالتالي:

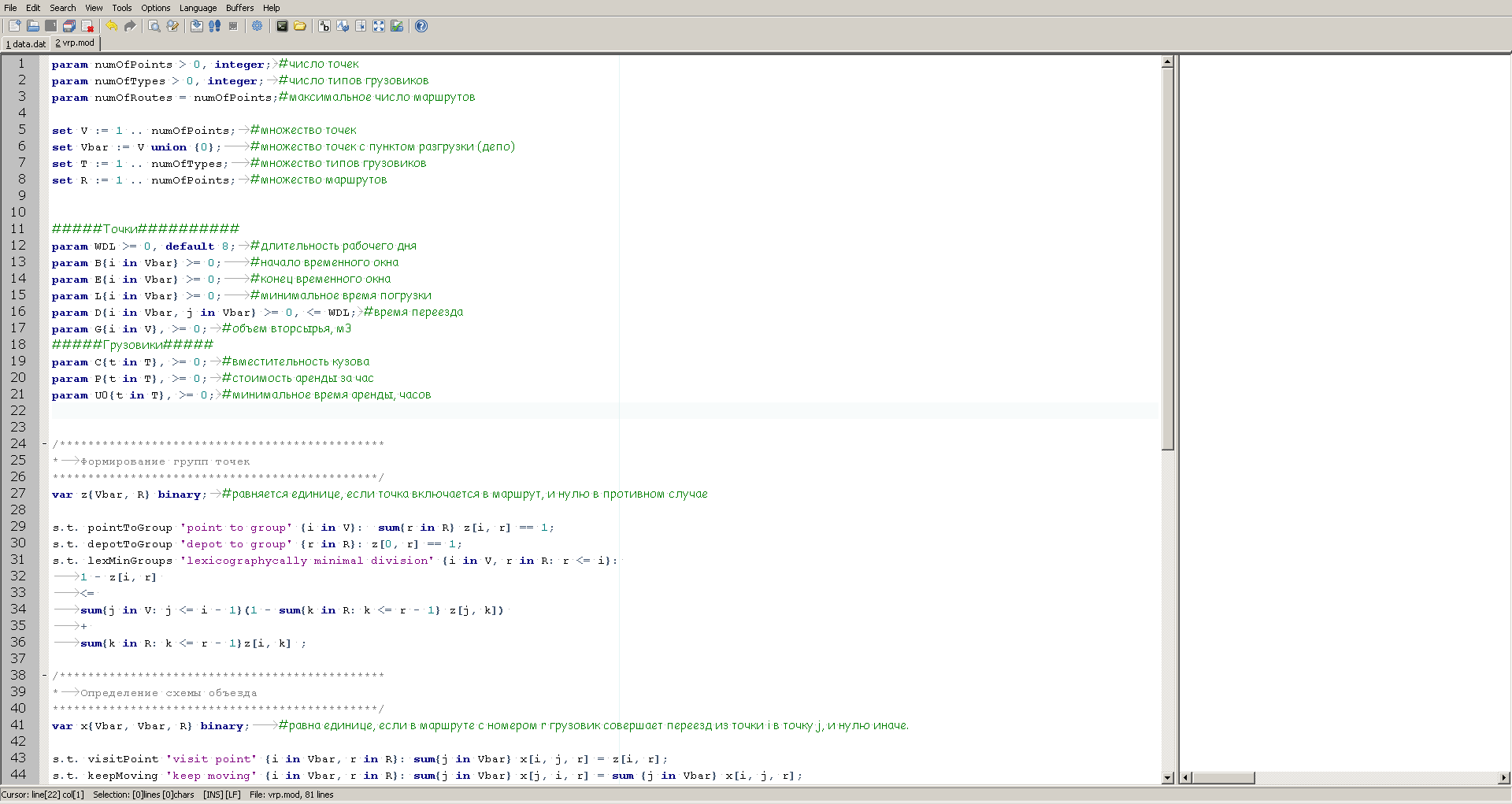
على اليسار ، نرى وصفًا للنموذج ، وعلى الجانب الأيمن هناك نافذة لعرض المعلومات حول تقدم الحساب ، والذي سيوفره المحلل بعد الإطلاق.

وصف كامل للنموذج

param numOfPoints > 0, integer; #  param numOfTypes > 0, integer; #   param numOfRoutes = numOfPoints;#   set V := 1 .. numOfPoints; #  set Vbar := V union {0}; #     () set T := 1 .. numOfTypes; #   set R := 1 .. numOfPoints; #  ############### param WDL >= 0, default 8; #   param B{i in Vbar} >= 0; #   param E{i in Vbar} >= 0; #   param L{i in Vbar} >= 0; #   param D{i in Vbar, j in Vbar} >= 0, <= WDL; #  param G{i in V}, >= 0; # , 3 ########## param C{t in T}, >= 0; #  param P{t in T}, >= 0; #    param U0{t in T}, >= 0; #  ,  /********************************************** *    **********************************************/ var z{Vbar, R} binary; # ,     ,      st pointToGroup 'point to group' {i in V}: sum{r in R} z[i, r] == 1; st depotToGroup 'depot to group' {r in R}: z[0, r] == 1; st lexMinGroups 'lexicographycally minimal division' {i in V, r in R: r <= i}: 1 - z[i, r] <= sum{j in V: j <= i - 1}(1 - sum{k in R: k <= r - 1} z[j, k]) + sum{k in R: k <= r - 1}z[i, k] ; /********************************************** *    **********************************************/ var x{Vbar, Vbar, R} binary; # ,    c  r      i   j,   . st visitPoint 'visit point' {i in Vbar, r in R}: sum{j in Vbar} x[i, j, r] = z[i, r]; st keepMoving 'keep moving' {i in Vbar, r in R}: sum{j in Vbar} x[j, i, r] = sum {j in Vbar} x[i, j, r]; var f{Vbar, Vbar, R} >= 0; #,  . st flowFromDepot 'flow from depot' {r in R}: sum{i in V} f[0, i, r] == sum{i in V} z[i, r]; st flowAlongActiveArcs 'flow along active arcs' {i in Vbar, j in Vbar, r in R}: f[i, j, r] <= numOfPoints * x[i, j, r]; st flowConservation 'flow conservation' {i in V, r in R}: sum{j in Vbar} f[j, i, r] == sum{j in Vbar} f[i, j, r] + z[i, r]; var a{i in V} >= 0; #     var w{i in Vbar, r in R} >= 0; #     st wait 'wait'{i in Vbar, r in R}: w[i, r] >= L[i] * z[i, r]; st dontWait 'dont wait'{i in Vbar, r in R}: w[i, r] <= (E[i] - B[i]) * z[i, r]; st arrivalTime 'arrival time' {i in V, j in V}: a[i] + sum{r in R}w[i, r] + D[i,j] <= a[j] + 3 * WDL * (1 - sum{r in R} x[i, j, r]); st arriveAfter 'arrive after' {i in V}: a[i] >= B[i]; st departBefore 'depart before' {i in V}: a[i] + sum{r in R}w[i, r] <= E[i]; /********************************************** *   ,       **********************************************/ var y{t in T, r in R}, binary; # ,    t       r,   . var u{t in T, r in R}, integer, >= 0; #    t,     rst assignVehicle 'assign vehicle' {r in R}: sum{t in T} y[t,r] == 1; st rentTime 'rent time' {r in R, t in T}: u[t, r] >= sum{i in V, j in Vbar}D[i, j] * x[i, j, r] + sum{i in Vbar}w[i, r] - WDL * (1 - y[t, r]); st minRentTime 'minimal rent time' {r in R, t in T}: u[t, r] >= U0[t] * (y[t, r] - sum{i in V}z[i, r]); st noRent 'no rent' {t in T, r in R}: u[t, r] <= WDL * y[t, r]; st fitCapacity 'fit capacity' {r in R}: sum{i in V} G[i] * z[i, r] <= sum{t in T} C[t] * y[t, r]; minimize rentCost: sum{t in T, r in R} P[t] * u[t, r]; solve; /********************************************** *     **********************************************/ printf{i in V, r in R} (if 0.1 < z[i,r] then "point %s to group %s\n" else ""), i, r, z[i,r]; printf{r in R, i in Vbar, j in Vbar} (if 0.1 < x[i, j, r] then "route %s: %s -> %s\n" else ""), r, i, j; printf{i in V} "point %s arrive between %s and %s (actual = %s)\n", i, B[i], E[i], a[i]; end;

لبداية سريعة ، سأضيف أيضًا بيانات مأخوذة من رأسي معدّة للاستخدام في النموذج:

إدخال البيانات

 data; param numOfPoints := 9; #  param numOfTypes := 6; #   ############### param : B E L := 0 0 8 1 1 0 8 1 2 0 8 1 3 0 8 1 4 0 8 1 5 0 8 1 6 0 8 1 7 0 8 1 8 0 8 1 9 0 8 1; param D default 0 : 0 1 2 3 4 5 6 7 8 9 := 0 . . . . . . . . . . 1 0.1 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 2 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 3 0.4 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 4 0.4 0.4 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 5 0.1 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 6 0.5 0.5 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 7 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 8 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 9 0.5 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1; param G := 1 1 2 2 3 1 4 2 5 1 6 2 7 1 8 2 9 1; ########## param : C P := 1 8 500 2 10 500 3 14 600 4 18 650 5 25 700 6 35 800; param U0 default 2; #  ,  end;

بعد نسخ رمز النموذج إلى ملف يحمل الاسم ، على سبيل المثال ، model.mod ، وبيانات الإدخال إلى ملف data.dat ، يصبح كل شيء جاهزًا للتشغيل. وضعنا حداً لوقت الحساب البالغ 100 ثانية (يتم ذلك باستخدام المفتاح - الوقت [بالثواني]) ، وننقل المسار إلى الملف باستخدام بيانات الإدخال (باستخدام المفتاح -d [مسار الملف]) ،

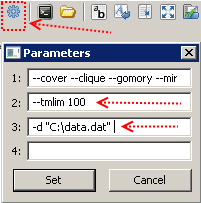
ثم اضغط F5. إذا نجحت ، ستظهر الرسائل في النافذة على اليمين ، وبعد مائة ثانية سيكون لدينا أفضل حل تمكنت GLPK من العثور عليه في الوقت المخصص.

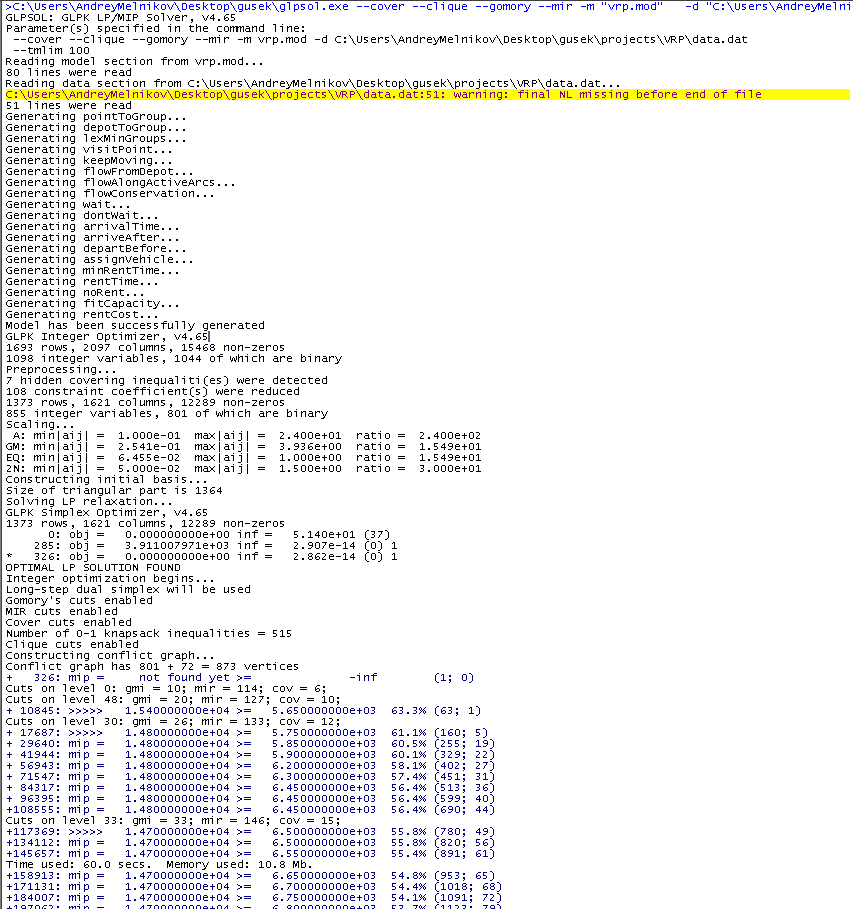
في النص الأزرق ، نحن مهتمون بالمعنى بعد النقش "mip =". كما ترون ، فإنه ينخفض من وقت لآخر. جميع الحلول الجديدة في طور العمل ، يتم عرض قيمة تكاليف النقل في أفضل حالاتها في هذا العمود (هناك 14700 حتى الآن). الرقم التالي هو الحد الأدنى للحصول على أفضل حل موجود ، أي الحل الأمثل . في البداية ، تم تقدير التقدير بشكل كبير ، ولكن تم تنقيحه بمرور الوقت ، أي الزيادات. تتقارب القيم الموجودة على اليسار وعلى اليمين ، والفجوة النسبية بينهما في وقت لقطة الشاشة هي 54.1٪. بمجرد أن يصبح هذا الرقم صفرًا ، ستثبت الخوارزمية أن أفضل حل ممكن هو الأفضل. ليس هناك ما يبرر دائمًا انتظار هذا الحدث في الممارسة العملية ، وليس فقط لأنه وقت طويل ، ولكن من المهم إجراء حجز ، كقاعدة عامة ، يكون الحل الجيد سريعًا نسبيًا ، وترتبط تكاليف الوقت الرئيسية بتنقيح التقدير المطلوب لإثبات أفضل ما يمكن.

بدلا من الاستنتاج

تعد مشكلات التوجيه معقدة للغاية من الناحية الحسابية ، ومع زيادة عدد النقاط التي تحتاج إلى زيارتها ، فإن الوقت الذي يستغرقه الحل لإيجاد حل وإثبات أن الأمثلية ينمو بسرعة. ومع ذلك ، للحصول على أمثلة صغيرة إلى حد ما ، في غضون فترة زمنية معقولة ، يكون حلالا قادرًا على إنشاء مجموعة ناجحة من الطرق ويمكن استخدامه لدعم صنع القرار. ساعدنا تحليل خيارات التوجيه التي اقترحها النموذج على اكتشاف فرص كبيرة لخفض التكاليف ، وهذا أمر بالغ الأهمية لوجود المخزون وتطويره.

ذهبت جهودنا الإضافية نحو العمل مع عدم اليقين في أحجام المواد القابلة لإعادة التدوير التي تم جمعها في النقاط. نحن نعمل على تطوير عدد من نماذج البرمجة العشوائية لاتخاذ القرارات الاستراتيجية والتشغيلية في توجيه الشاحنات. إذا كان الموضوع ذا صلة وأثار اهتمامًا ، فسأكتب عن هذا أيضًا ، لأنه قريبًا سيتعين علينا جميعًا أن نتعمق أكثر في القضايا البيئية ، وهذا ما أتمنى لنا النجاح فيه.

لوجستيات العمل من أجل مجموعة منفصلة من المواد القابلة لإعادة التدوير

بدلا من الانضمام

1. عمل "السنجاب الأخضر"

2. إضفاء الطابع الرسمي

ابحث عن حل

بدلا من الاستنتاج

More articles: