الشبكات العصبية والتعلم العميق ، الفصل 1: استخدام الشبكات العصبية للتعرف على الأرقام المكتوبة بخط اليد

تعليق

فيما يلي ترجمة لكتاب Michael Nielsen المجاني عبر الإنترنت Neural Networks and Deep Learning ، والذي تم توزيعه بموجب ترخيص Creative Commons Attribution-NonCommercial 3.0 Unported . كان الدافع وراء إنشائها هو التجربة الناجحة في ترجمة كتاب مدرسي ، Expressive JavaScript . يحظى كتاب الشبكات العصبية بشعبية كبيرة ؛ إذ يستشهد به مؤلفو المقالات باللغة الإنجليزية. لم أجد ترجماتها ، باستثناء ترجمة بداية الفصل الأول مع الاختصارات .

يمكن لأولئك الذين يرغبون في شكر مؤلف الكتاب القيام بذلك على صفحته الرسمية ، عن طريق التحويل عبر PayPal أو Bitcoin. لدعم المترجم على حبري ، هناك نموذج "لدعم المؤلف".

مقدمة

سيخبرك هذا البرنامج التعليمي بالتفصيل عن مفاهيم مثل:

• الشبكات العصبية - نموذج برمجي ممتاز ، تم إنشاؤه تحت تأثير علم الأحياء ، والسماح للكمبيوتر بالتعلم بناءً على الملاحظات.
• التعلم العميق هو مجموعة قوية من تقنيات التدريب على الشبكات العصبية.

توفر الشبكات العصبية (NS) والتعلم العميق (GO) اليوم أفضل حل للعديد من المشكلات في مجالات التعرف على الصور والصوت ومعالجة اللغة الطبيعية. سوف يعلمك هذا البرنامج التعليمي العديد من المفاهيم الأساسية التي تدعم NS و GO.

ما هو هذا الكتاب عنه

NS هي واحدة من أرقى نماذج البرامج التي اخترعها الإنسان على الإطلاق. من خلال نهج البرمجة القياسي ، فإننا نعلم الكمبيوتر بما يجب القيام به ، ونقسم المهام الكبيرة إلى العديد من المهام الصغيرة ، ونحدد بدقة المهام التي سوف يؤديها الكمبيوتر بسهولة. في حالة الجمعية الوطنية ، على العكس من ذلك ، لا نخبر الكمبيوتر بكيفية حل المشكلة. هو نفسه يتعلم هذا على أساس "الملاحظات" من البيانات ، "اختراع" حله الخاص لهذه المشكلة.

التعلم الآلي القائم على البيانات يبدو واعدا. ومع ذلك ، حتى عام 2006 ، لم نكن نعرف كيفية تدريب الجمعية الوطنية حتى يتسنى لها تجاوز النهج التقليدية ، باستثناء بعض الحالات الخاصة. في عام 2006 ، تقنيات التدريب لما يسمى الشبكات العصبية العميقة (GNS). الآن تعرف هذه التقنيات باسم التعلم العميق (GO). استمر تطويرها ، وحققت GNS و GO اليوم نتائج مذهلة في العديد من المهام الهامة المتعلقة برؤية الكمبيوتر والتعرف على الكلام ومعالجة اللغة الطبيعية. على نطاق واسع ، يتم نشرها بواسطة شركات مثل Google و Microsoft و Facebook.

الغرض من هذا الكتاب هو مساعدتك في إتقان المفاهيم الأساسية للشبكات العصبية ، بما في ذلك تقنيات GO الحديثة. بعد العمل مع البرنامج التعليمي ، سوف تكتب رمزًا يستخدم NS و GO لحل المشكلات المعقدة المتمثلة في التعرف على الأنماط. سيكون لديك أساس لاستخدام NS والدفاع المدني في النهج لحل المشاكل الخاصة بك.

النهج القائم على مبدأ

أحد المعتقدات التي يقوم عليها الكتاب هو أنه من الأفضل الحصول على فهم راسخ للمبادئ الرئيسية للجمعية الوطنية والمجتمع المدني بدلاً من الحصول على المعرفة من قائمة طويلة من الأفكار المختلفة. إذا كان لديك فهم جيد للأفكار الرئيسية ، فسوف تفهم بسرعة مواد جديدة أخرى. بلغة المبرمج ، يمكننا القول أننا سندرس بناء الجملة الأساسي والمكتبات وهياكل البيانات للغة الجديدة. قد تتعرف على جزء صغير فقط من اللغة بأكملها - العديد من اللغات بها مكتبات قياسية هائلة - ومع ذلك ، يمكنك فهم المكتبات الجديدة وهياكل البيانات بسرعة وسهولة.

لذلك ، هذا الكتاب ليس بشكل قاطع مواد تعليمية حول كيفية استخدام أي مكتبة معينة للجمعية الوطنية. إذا كنت تريد فقط معرفة كيفية العمل مع المكتبة - لا تقرأ الكتاب! ابحث عن المكتبة التي تحتاج إليها واعمل مع المواد والوثائق التدريبية. لكن ضع في اعتبارك: على الرغم من أن هذا النهج له ميزة حل المشكلة على الفور ، إذا كنت ترغب في فهم ما يحدث بالضبط داخل الجمعية الوطنية ، إذا كنت ترغب في إتقان الأفكار التي ستكون ذات صلة في سنوات عديدة ، فلن يكون كافياً بالنسبة لك ببساطة دراسة نوع من مكتبة الموضة. تحتاج إلى فهم الأفكار الموثوقة والطويلة الأجل التي تقوم عليها أعمال الجمعية الوطنية. التكنولوجيا تأتي وتذهب والأفكار تستمر إلى الأبد.

النهج العملي

سنقوم بدراسة المبادئ الأساسية على سبيل المثال لمهمة محددة: تعليم الكمبيوتر التعرف على الأرقام المكتوبة بخط اليد. باستخدام أساليب البرمجة التقليدية ، هذه المهمة صعبة للغاية لحلها. ومع ذلك ، يمكننا حلها بشكل جيد مع NS بسيطة وعشرات الأسطر من التعليمات البرمجية ، دون أي مكتبات خاصة. علاوة على ذلك ، سوف نقوم بتحسين هذا البرنامج تدريجياً ، بما في ذلك باستمرار الأفكار الرئيسية حول الجمعية الوطنية والدفاع المدني.

هذا النهج العملي يعني أنك ستحتاج إلى بعض الخبرة في البرمجة. لكن لا يجب أن تكون مبرمجًا محترفًا. كتبت رمز الثعبان (الإصدار 2.7) الذي يجب أن يكون واضحا حتى لو لم تكتب برامج الثعبان. في عملية الدراسة ، سنقوم بإنشاء مكتبتنا الخاصة للجمعية الوطنية ، والتي يمكنك استخدامها للتجارب والتدريب الإضافي. كل رمز يمكن تحميلها هنا . بعد الانتهاء من الكتاب ، أو في عملية القراءة ، يمكنك اختيار واحدة من المكتبات الأكثر اكتمالا للجمعية الوطنية ، وتكييفها للاستخدام في هذه المشاريع.

المتطلبات الرياضية لفهم المواد متوسطة للغاية. تحتوي معظم الفصول على أجزاء رياضية ، ولكنها عادةً ما تكون عبارة عن جبر أولي ورسوم بيانية وظيفية. أحيانًا أستخدم رياضيات أكثر تقدماً ، لكنني نظّمت المادة بحيث يمكنك فهمها ، حتى لو كانت بعض التفاصيل بعيدة عنك. يتم استخدام معظم الرياضيات في الفصل 2 ، والذي يتطلب بعض الشيء من التحليل الزوجي والجبر الخطي. بالنسبة لأولئك الذين ليسوا على دراية بهم ، أبدأ الفصل 2 بمقدمة في الرياضيات. إذا وجدت صعوبة ، فقط تخطي الفصل حتى يتم استخلاص المعلومات. في أي حال ، لا تقلق بشأن هذا.

نادرًا ما يتم توجيه الكتاب نحو فهم المبادئ والنهج العملي. لكنني أعتقد أنه من الأفضل أن تدرس على أساس الأفكار الأساسية للجمعية الوطنية. سنكتب رمز العمل ، وليس فقط دراسة النظرية المجردة ، ويمكنك استكشاف وتوسيع هذا الرمز. بهذه الطريقة ، ستفهم الأساسيات ، النظرية والتطبيق ، وستكون قادرًا على التعلم أكثر.

التمارين والمهام

غالبًا ما يحذر مؤلفو الكتب الفنية القارئ من أنه يحتاج ببساطة إلى إكمال جميع التدريبات وحل جميع المشكلات. عند قراءة هذه التحذيرات لي ، فإنها تبدو دائمًا غريبة بعض الشيء. هل سيحدث لي شيء سيء إذا لم أقم بإجراء التمارين وحل المشكلات؟ لا بالطبع. سأوفر فقط الوقت من خلال فهم أقل عمقا. في بعض الأحيان الأمر يستحق ذلك. في بعض الأحيان لا.

ما الذي يستحق القيام به مع هذا الكتاب؟ أنصحك بمحاولة إكمال معظم التمارين ، لكن لا تحاول حل معظم المهام.

تحتاج معظم التدريبات إلى الانتهاء لأن هذه اختبارات أساسية لفهم المادة بشكل صحيح. إذا لم تتمكن من أداء التمرين بسهولة نسبية ، فيجب أن تكون قد فاتتك شيء أساسي. بالطبع ، إذا كنت عالقًا حقًا في نوع من التمرين - أسقطه ، ربما يكون هذا نوعًا من سوء التفاهم الصغير ، أو ربما قمت بصياغة شيء سيء. ولكن إذا تسببت معظم التمارين في صعوبة ، فأنت بحاجة على الأرجح إلى إعادة قراءة المادة السابقة.

المهام هي مسألة أخرى. إنها أكثر صعوبة من التمارين ، وستواجه مع البعض وقتًا عصيبًا. هذا أمر مزعج ، ولكن بالطبع الصبر في مواجهة مثل هذا الإحباط هو الطريقة الوحيدة لفهم واستيعاب الموضوع حقًا.

لذلك أنا لا أوصي حل جميع المشاكل. الأفضل من ذلك - اختيار المشروع الخاص بك. قد ترغب في استخدام NS لتصنيف مجموعتك الموسيقية. أو للتنبؤ بقيمة الأسهم. أو أي شيء آخر. ولكن العثور على مشروع مثير للاهتمام بالنسبة لك. وبعد ذلك يمكنك تجاهل المهام من الكتاب ، أو استخدامها بحتة كمصدر إلهام للعمل في مشروعك. سوف تعلمك مشاكل مشروعك أكثر من العمل مع أي عدد من المهام. المشاركة العاطفية هي عامل رئيسي في تحقيق التمكن.

بالطبع ، بينما قد لا يكون لديك مثل هذا المشروع. هذا طبيعي. حل المهام التي تشعرك بدافع جوهري. استخدم مواد من الكتاب لمساعدتك في العثور على أفكار لمشاريع إبداعية شخصية.

الفصل 1

النظام البصري البشري هو واحد من عجائب العالم. النظر في التسلسل التالي من الأرقام المكتوبة بخط اليد:



سوف يقرأها معظم الناس بسهولة ، مثل 504192. لكن هذه البساطة خادعة. في كل نصف الكرة من الدماغ ، يكون لدى الشخص قشرة بصرية أولية ، تعرف أيضًا باسم V1 ، والتي تحتوي على 140 مليون خلية عصبية وعشرات المليارات من الروابط بينهما. في الوقت نفسه ، لا تشارك V1 فقط في الرؤية البشرية ، ولكن سلسلة كاملة من مناطق الدماغ - V2 و V3 و V4 و V5 - التي تعمل في معالجة الصور بشكل متزايد التعقيد. نحمل في رؤوسنا حاسوبًا عملاقًا تم ضبطه بالتطور لمئات الملايين من السنين ، وتم تكييفه تمامًا لفهم العالم المرئي. التعرف على الأرقام المكتوبة بخط اليد ليس بالأمر السهل. إنه فقط لأننا ، بشكل مدهش ومثير للدهشة ، ندرك ما تظهره أعيننا. ولكن يتم تنفيذ كل هذا العمل تقريبًا دون وعي. وعادة لا نعلق أهمية على المهمة الصعبة التي تحلها أنظمتنا البصرية.

تصبح صعوبة التعرف على الأنماط المرئية واضحة عند محاولة كتابة برنامج كمبيوتر للتعرف على الأرقام مثل تلك المذكورة أعلاه. ما يبدو سهلا في إعدامنا فجأة تبين أنه معقد للغاية. إن المفهوم البسيط للكيفية التي نتعرف بها على النماذج - "التسعة بها حلقة في الأعلى والشريط العمودي في أسفل اليمين" - ليس بهذه البساطة على الإطلاق لتعبير حسابي. من خلال محاولة توضيح هذه القواعد بوضوح ، تتعثر بسرعة في مستنقع من الاستثناءات والمزالق والمناسبات الخاصة. المهمة تبدو ميؤوس منها.

NS نهج لحل المشكلة بطريقة مختلفة. والفكرة هي أن تأخذ العديد من الأرقام المكتوبة بخط اليد المعروفة باسم أمثلة التدريس ،



وتطوير نظام يمكنه التعلم من هذه الأمثلة. بمعنى آخر ، تستخدم الجمعية الوطنية أمثلة لإنشاء قواعد التعرف على الأرقام المكتوبة بخط اليد تلقائيًا. علاوة على ذلك ، من خلال زيادة عدد أمثلة التدريب ، يمكن للشبكة معرفة المزيد عن الأرقام المكتوبة بخط اليد وتحسين دقتها. لذلك ، على الرغم من أنني ذكرت أعلاه أكثر من 100 دراسة حالة ، ربما يمكننا إنشاء نظام أفضل للتعرف على خط اليد باستخدام الآلاف أو حتى الملايين والمليارات من دراسات الحالة.

في هذا الفصل ، سنكتب برنامج كمبيوتر يقوم بتنفيذ NS لتعلم التعرف على الأرقام المكتوبة بخط اليد. سيكون البرنامج 74 خطًا فقط ولن يستخدم مكتبات خاصة للجمعية الوطنية. ومع ذلك ، سيتمكن هذا البرنامج القصير من التعرف على الأرقام المكتوبة بخط اليد بدقة تزيد عن 96٪ ، دون الحاجة إلى تدخل بشري. علاوة على ذلك ، في الفصول المستقبلية ، سنقوم بتطوير أفكار يمكنها تحسين الدقة إلى 99٪ أو أكثر. في الواقع ، تقوم أفضل NS NS تجارية بعمل جيد بحيث تستخدمها البنوك لمعالجة الشيكات ، والخدمات البريدية للتعرف على العناوين.

نحن نركز على التعرف على خط اليد ، لأن هذا نموذج رائع لمهمة دراسة NS. مثل هذا النموذج الأولي مثالي بالنسبة لنا: إنه مهمة صعبة (التعرف على الأرقام المكتوبة بخط اليد ليس بالمهمة السهلة) ، ولكن ليس معقدًا لدرجة أنه يتطلب حلاً معقدًا للغاية أو قوة حوسبية هائلة. علاوة على ذلك ، هذه طريقة رائعة لتطوير تقنيات أكثر تعقيدًا ، مثل GO. لذلك ، في الكتاب سنعود باستمرار إلى مهمة التعرف على خط اليد. سنناقش لاحقًا كيف يمكن تطبيق هذه الأفكار على المهام الأخرى المتمثلة في رؤية الكمبيوتر ، والتعرف على الكلام ، ومعالجة اللغة الطبيعية وغيرها من المجالات.

بالطبع ، إذا كان الغرض من هذا الفصل هو فقط كتابة برنامج للتعرف على الأرقام المكتوبة بخط اليد ، فسيكون الفصل أقصر بكثير! ومع ذلك ، في هذه العملية ، سنقوم بتطوير العديد من الأفكار الرئيسية المتعلقة NS ، بما في ذلك نوعين مهمين من الخلايا العصبية الاصطناعية ( perceptron والخلايا العصبية السيني) ، وخوارزمية التعلم NS القياسية ، النسب التدرج العشوائي . في النص ، أركز على شرح سبب القيام بكل شيء بهذه الطريقة ، وعلى تشكيل فهمك للجمعية الوطنية. هذا يتطلب محادثة أطول مما لو كنت قد عرضت للتو الآليات الأساسية لما يحدث ، ولكن الأمر يتطلب فهماً أعمق. من بين المزايا الأخرى - بحلول نهاية الفصل ، سوف تفهم ماهية الدفاع المدني ولماذا هو مهم جدًا.

بيرسيبترون

ما هي الشبكة العصبية؟ للبدء ، سأتحدث عن نوع واحد من الخلايا العصبية المصطنعة يسمى البسبترون. تم اختراع البسبترون من قبل العالم فرانك روزنبلات في الخمسينيات والستينيات ، مستوحاة من الأعمال المبكرة لوارن ماكالوك ووالتر بيتس . اليوم ، يتم استخدام نماذج أخرى من الخلايا العصبية الاصطناعية في كثير من الأحيان - في هذا الكتاب ، ومعظم الأعمال الحديثة على NS تستخدم بشكل رئيسي نموذج السيني من الخلايا العصبية. سنلتقي بها قريبا. ولكن لفهم سبب تعريف الخلايا العصبية السينيّة بهذه الطريقة ، فإن الأمر يستحق قضاء الوقت في تحليل الإدراك الحسي.

إذا كيف يعمل الإدراك الحسي؟ يستقبل الإدراك الحسي عدة أرقام ثنائية × ₁ ، × ₂ ، ... ويعطي رقمًا ثنائيًا واحدًا:



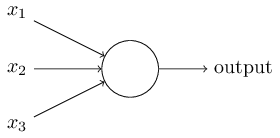
في هذا المثال ، يوجد في perceptron ثلاثة أرقام إدخال ، x ₁ ، x ₂ ، x ₃ . بشكل عام ، قد يكون هناك أكثر أو أقل منهم. اقترح روزنبلات قاعدة بسيطة لحساب النتيجة. قدم الأوزان ، w ₁ ، w ₂ ، أرقام حقيقية ، معربًا عن أهمية أرقام المدخلات المقابلة للنتائج. يتم تحديد ناتج الخلايا العصبية ، 0 أو 1 ، من خلال ما إذا كان المبلغ المرجح أقل أو أكثر من عتبة معينة [عتبة] $$$\ sum_j w_jx_j$ . مثل الأوزان ، العتبة هي رقم حقيقي ، معلمة من الخلايا العصبية. في المصطلحات الرياضية:

$$

$$output = \ start {cases} 0 ~ if ~ \ sum_j w_jx_j \ leq threshold \\ 1 ~ if ~ \ sum_j w_jx_j> العتبة \ end {cases} \ tag {1}$$

هذا هو الوصف الكامل لل perceptron!

هذا هو النموذج الرياضي الأساسي. يمكن التفكير في الإدراك الحسي باعتباره صانع قرار من خلال تقييم الأدلة. اسمحوا لي أن أقدم لكم مثالاً غير واقعي للغاية ، ولكن بسيط. دعنا نقول أن عطلة نهاية الأسبوع قادمة ، وسمعت أن مهرجان الجبن سيعقد في مدينتك. تحب الجبن ، وحاول أن تقرر ما إذا كنت ستذهب إلى المهرجان أم لا. يمكنك اتخاذ قرار بوزن ثلاثة عوامل:

1. هل الطقس جيد؟
2. هل شريكك يريد أن يذهب معك؟
3. هل المهرجان بعيد عن المواصلات العامة؟ (ليس لديك سيارة).

يمكن تمثيل هذه العوامل الثلاثة كمتغيرات ثنائية × ₁ ، × ₂ ، × ₃ . على سبيل المثال ، × ₁ = 1 إذا كان الطقس جيدًا ، و 0 إذا كان سيئًا. × ₂ = 1 إذا كان شريكك يريد الذهاب ، و 0 إذا لم يكن كذلك. نفس الشيء بالنسبة إلى x ₃ .

الآن ، لنفترض أنك معجب جدًا بالجبن لدرجة أنك على استعداد للذهاب إلى المهرجان ، حتى لو كان شريكك غير مهتم به ومن الصعب الوصول إليه. لكن ربما تكره الطقس السيئ ، وفي حالة الطقس السيئ ، لن تذهب إلى المهرجان. يمكنك استخدام perceptrons لتصميم عملية صنع القرار هذه. إحدى الطرق هي اختيار الوزن w ₁ = 6 للطقس ، w ₂ = 2 ، w ₃ = 2 للحالات الأخرى. قيمة أكبر من w ₁ تعني أن الطقس يهمك أكثر بكثير مما إذا كان شريكك سينضم إليك أو بالقرب من المهرجان. أخيرًا ، لنفترض أنك حددت العتبة 5. لـ perceptron ، وبهذه الخيارات ، يقوم perceptron بتطبيق نموذج القرار المرغوب ، مع إعطاء 1 عندما يكون الطقس جيدًا و 0 عندما يكون سيئًا. لا تؤثر رغبة الشريك وقرب التوقف على قيمة الإخراج.

من خلال تغيير الأوزان والعتبات ، يمكننا الحصول على نماذج مختلفة لصنع القرار. على سبيل المثال ، دعنا نقول أننا نأخذ العتبة 3. ثم يقرر المدافع أنك بحاجة للذهاب إلى المهرجان ، إما عندما يكون الطقس لطيفًا ، أو عندما يكون المهرجان بالقرب من محطة للحافلات ويوافق شريكك على الذهاب معك. بمعنى آخر ، النموذج مختلف. إن تخفيض العتبة يعني أنك تريد الذهاب إلى المهرجان أكثر.

من الواضح أن الإدراك الحسي ليس نموذجًا كاملًا لاتخاذ القرارات البشرية! لكن هذا المثال يوضح كيف يمكن لمدرك الإدراك أن يزن أنواعًا مختلفة من الأدلة لاتخاذ القرارات. يبدو من الممكن أن شبكة معقدة من الإدراك الحسي يمكن أن تتخذ قرارات معقدة للغاية:



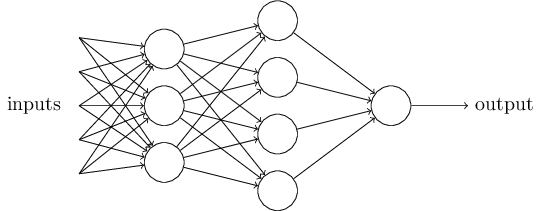
في هذه الشبكة ، يتخذ العمود الأول من الإدراك الحسي - ما نسميه الطبقة الأولى من الإدراك الحسي - ثلاثة قرارات بسيطة للغاية ، تزن أدلة المدخلات. ماذا عن الإدراك الحسي من الطبقة الثانية؟ يتخذ كل منهم قرارًا ، يزن نتائج طبقة اتخاذ القرار الأولى. وبهذه الطريقة ، يمكن لمدرك الطبقة الثانية أن يتخذ قرارًا على مستوى أكثر تعقيدًا وتجريدًا مقارنةً بمصور الطبقة الأولى. وحتى القرارات الأكثر تعقيدًا يمكن أن يتخذها المدركون على الطبقة الثالثة.وبهذه الطريقة ، يمكن لشبكة متعددة الطبقات من الإدراك الحسي التعامل مع القرارات المعقدة.

بالمناسبة ، عندما حددت المدرك ، قلت أن له قيمة إخراج واحدة فقط. ولكن في الشبكة في الأعلى ، يبدو أن الإدراك الحسي لديهم قيم إخراج متعددة. في الواقع ، لديهم طريقة واحدة فقط للخروج. العديد من أسهم الإخراج هي مجرد وسيلة مناسبة لإظهار أن إخراج perceptron يستخدم كمدخلات من perceptrons الأخرى. هذا أقل تعقيدًا من رسم مخرج متفرع واحد.

دعونا تبسيط وصف perceptrons. حالة$$Σ ي من ث ي س ي > ر ص بريد ق ح س ل د محرجا، ونحن يمكن أن نتفق على اثنين من التغييرات لتسجيل بساطته. الأول هو تسجيل$\sum_j w_jx_j > treshold$$$Σ ي من ث ي س ي كمنتج مفردة،$\sum_j w_jx_j$$$w ⋅ x = ∑ j w j x j ، حيث w و x عبارة عن متجهين تكون مكوناتهما عبارة عن أوزان وبيانات إدخال ، على التوالي. والثاني هو نقل العتبة إلى جزء آخر من عدم المساواة ، واستبدالها بقيمة تُعرف بالإزاحة المدركة [bias] ،$w \cdot x = \sum_j w_jx_j$$$$b \equiv −threshold$ . باستخدام الإزاحة بدلاً من العتبة ، يمكننا إعادة كتابة قاعدة المدرك:

$$

$$output = \begin{cases} 0 ~ if ~ w \cdot x + b \leq 0 \\ 1 ~ if ~ w \cdot x + b > 0 \end{cases} \tag{2}$$

يمكن تمثيل الإزاحة كمقياس لمدى سهولة الحصول على قيمة 1 عند الإخراج من الإدراك الحسي. أو ، من الناحية البيولوجية ، فإن النزوح هو مقياس لمدى سهولة تنشيط الإدراك الحسي. من السهل للغاية إعطاء المُدْرِجَة ذات التحيز الكبير جدًا 1. لكن مع التحيز السلبي الكبير جدًا ، يصعب القيام بذلك. من الواضح أن إدخال التحيز هو تغيير بسيط في وصف الإدراك الحسي ، لكننا سنرى لاحقًا أنه يؤدي إلى مزيد من التبسيط للتسجيل. لذلك ، لن نستخدم العتبة ، لكننا سنستخدم دائمًا الإزاحة.

وصفت perceptrons من حيث طريقة وزن الأدلة لاتخاذ القرارات. هناك طريقة أخرى لاستخدامها وهي حساب الدالات المنطقية الأولية ، والتي نعتبرها عادة الحسابات الرئيسية ، مثل AND و OR و NAND. لنفترض ، على سبيل المثال ، أن لدينا مدرك مع اثنين من المدخلات ، وزن كل منها -2 ، وإزاحته 3. هنا هو: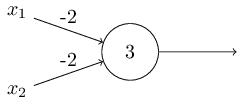



الإدخال 00 يعطي الناتج 1 ، لأن ()2) ∗ 0 + (- 2) ) ∗ 0 + 3 = 3 أكبر من الصفر. نفس الحسابات تقول أن المدخلات 01 و 10 تعطي 1. لكن 11 عند المدخل تعطي 0 عند الخرج ، لأن ()2) ∗ 1 + (- 2) ∗ 1 + 3 = −1 ، أقل من الصفر. لذلك ، لدينا perceptron تنفذ وظيفة NAND!

يوضح هذا المثال أنه يمكن استخدام الإدراك الحسي لحساب وظائف المنطق الأساسية. في الواقع ، يمكننا استخدام شبكات perceptron لحساب أي وظائف منطقية بشكل عام. الحقيقة هي أن بوابة منطق NAND عالمية للحسابات - من الممكن بناء أي حسابات على أساسها. على سبيل المثال ، يمكنك استخدام بوابات NAND لإنشاء دائرة تضيف جزئين ، x ₁ و x ₂ . للقيام بذلك ، حساب المبلغ bitwise$$x 1 ⊕ x 2 ، وكذلكعلامة الحمل، والتي تكون 1 عندما تكون كل من x₁و x₂هي 1 - أي أن علامة الحمل هي ببساطة نتيجة الضرب bitwise x₁x₂:للحصول على الشبكة المكافئة من perceptrons ، نستبدل الكل بوابات NAND هي perceptrons مع اثنين من المدخلات ، وزن كل منها -2 ، مع إزاحة 3. هنا هي الشبكة الناتجة. 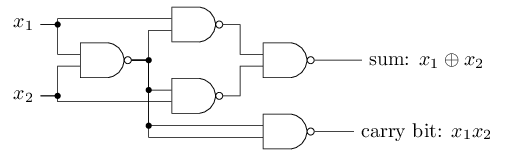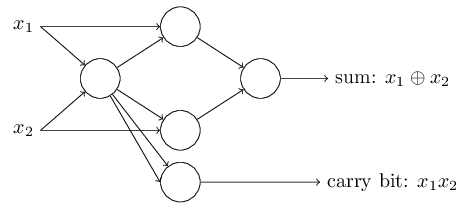لاحظ أنني قمت بنقل جهاز الإدراك المتوافق مع الصمام الأيمن السفلي ، فقط لجعله أكثر ملاءمة لرسم الأسهم:$x_1 \oplus x_2$







أحد الجوانب الجديرة بالملاحظة في شبكة perceptron هذه هو أن ناتج أقصى اليسار يستخدم مرتين كمدخلات في الأسفل. من خلال تحديد نموذج المدخل ، لم أذكر مقبولية مخطط الخروج المزدوج في نفس المكان. في الواقع ، لا يهم حقا. إذا كنا لا نريد السماح بذلك ، فيمكننا ببساطة دمج خطين مع أوزان -2 في واحد بوزن -4. (إذا كان هذا لا يبدو واضحًا لك ، فتوقف واثبت ذلك بنفسك). بعد هذا التغيير ، تبدو الشبكة على النحو التالي ، حيث تساوي جميع الأوزان غير المخصصة -2 ، وجميع الإزاحات تساوي 3 ، ويتم تمييز وزن واحد -4:



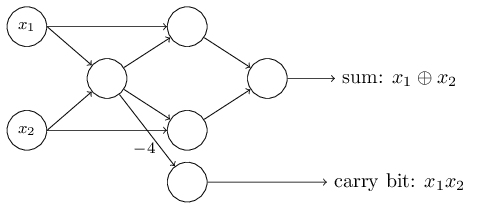مثل هذا السجل من الإدراك الحسي الذي يكون له ناتج ولكن بدون مدخلات:



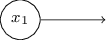هو مجرد اختصار. هذا لا يعني أنه ليس لديه مدخلات. لفهم هذا ، افترض أن لدينا مدرك بدون مدخلات. عندئذٍ ، سيكون المجموع المرجح هو zero _j w _j x _j صفراً ، لذا فإن perceptron ستعطي 1 لـ b> 0 و 0 لـ b ≤ 0. وهذا يعني أن perceptron سيعطي قيمة ثابتة فقط وليس ما نحتاج إليه (x ₁ في المثال أعلاه). من الأفضل اعتبار مدخلات الإدراك ليس كإدخالات مدركة ، ولكن كوحدات خاصة يتم تعريفها ببساطة لإنتاج القيم المطلوبة × ₁ ، × ₂ ، ...

يوضح مثال adder كيف يمكن استخدام شبكة perceptron لمحاكاة دائرة تحتوي على العديد من بوابات NAND. ونظرًا لأن هذه البوابات عالمية بالنسبة للحسابات ، لذلك فإن الإدخالات الحسية عالمية للحسابات.

براعة حسابية من perceptrons مشجعة ومخيبة للآمال. إنه لأمر مشجع ، التأكد من أن شبكة perceptron يمكن أن تكون قوية مثل أي جهاز كمبيوتر آخر. مخيبة للآمال ، إعطاء الانطباع بأن الإدراك الحسي ليست سوى نوع جديد من بوابة المنطق NAND. اكتشاف ذلك!

ومع ذلك ، فإن الوضع هو في الواقع أفضل. اتضح أنه يمكننا تطوير خوارزميات تدريب يمكنها ضبط الأوزان والتشريد في الشبكة تلقائيًا من الخلايا العصبية الاصطناعية. يحدث هذا الضبط استجابة للمنبهات الخارجية ، دون تدخل مباشر من مبرمج. تسمح لنا خوارزميات التعلم هذه باستخدام عصبونات اصطناعية بطريقة تختلف جذريًا عن البوابات المنطقية العادية. بدلاً من تسجيل دائرة بشكل صريح من بوابات NAND وغيرها ، يمكن لشبكاتنا العصبية ببساطة أن تتعلم كيفية حل المشاكل ، وأحيانًا تلك التي سيكون من الصعب للغاية تصميمها بشكل منتظم.

الخلايا العصبية السيني

خوارزميات التعلم رائعة. ومع ذلك ، كيفية تطوير مثل هذه الخوارزمية لشبكة العصبية؟ لنفترض أن لدينا شبكة من الإدراك الحسي الذي نريد استخدامه لتدريبنا على حل مشكلة ما. افترض أن الإدخال إلى الشبكة قد يكون بكسل لصورة ممسوحة ضوئيًا من رقم مكتوب بخط اليد. ونريد أن تعرف الشبكة الأوزان والإزاحات اللازمة لتصنيف الأرقام بشكل صحيح. لفهم كيف يمكن لهذا التدريب أن يعمل ، فلنتخيل أننا نغير قليلاً من الوزن (أو التحيز) في الشبكة. نريد أن يؤدي هذا التغيير البسيط إلى تغيير بسيط في إخراج الشبكة. كما سنرى قريبًا ، فإن هذه الخاصية تجعل التعلم ممكنًا. من الناحية التخطيطية ، نريد ما يلي (من الواضح أن مثل هذه الشبكة بسيطة جدًا للتعرف على خط اليد!):



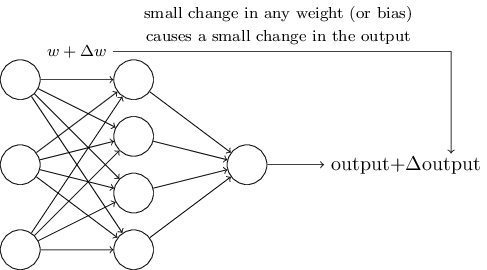
إذا أدى تغيير بسيط في الوزن (أو الانحياز) إلى تغيير بسيط في نتيجة المخرجات ، فيمكننا تغيير الأوزان والتحيزات بحيث تتصرف شبكتنا بشكل أقرب قليلاً إلى ما نريد. على سبيل المثال ، دعنا نقول أن الشبكة قد عيّنت الصورة بشكل غير صحيح على "8" ، على الرغم من أنه كان يجب أن تكون "9". يمكننا معرفة كيفية إجراء تغيير طفيف في الوزن والإزاحة بحيث تقترب الشبكة قليلاً من تصنيف الصورة على أنها "9". وبعد ذلك نكرر هذا ، مع تغيير الأوزان والتحولات مرارًا وتكرارًا للحصول على أفضل وأفضل نتيجة. سوف تتعلم الشبكة.

المشكلة هي أنه إذا كان هناك تصورات في الشبكة ، فإن هذا لا يحدث. قد يؤدي التغيير الطفيف في الأوزان أو الإزاحة لأي مدرك في بعض الأحيان إلى تغيير في ناتجها إلى الاتجاه المعاكس ، على سبيل المثال ، من 0 إلى 1. مثل هذا الوجه يمكن أن يغير سلوك بقية الشبكة بطريقة معقدة للغاية. وحتى إذا تم الآن التعرف على الرقم "9" بشكل صحيح ، فمن المحتمل أن سلوك الشبكة مع جميع الصور الأخرى قد تغير تمامًا بطريقة يصعب التحكم فيها. لهذا السبب ، من الصعب تخيل كيف يمكننا ضبط الأوزان والإزاحة تدريجياً بحيث تقترب الشبكة تدريجياً من السلوك المرغوب. ربما هناك طريقة ذكية للتغلب على هذه المشكلة. ولكن لا يوجد حل بسيط لمشكلة تعلم شبكة من الإدراك الحسي.

يمكن التغلب على هذه المشكلة عن طريق إدخال نوع جديد من الخلايا العصبية الاصطناعية يسمى العصب السيني. إنها تشبه الإدراك الحسي ، ولكنها تُعدل بحيث تؤدي التغييرات الصغيرة في الأوزان والإزاحة إلى تغييرات صغيرة فقط في المخرجات. هذه حقيقة أساسية ستسمح لشبكة الخلايا العصبية السينيّة بالتعلم.

اسمحوا لي أن أصف الخلايا العصبية السيني. سوف نرسمها بنفس طريقة الإدراك الحسي:



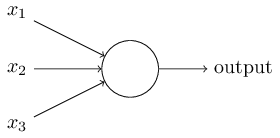
يحتوي على نفس المدخلات x ₁ ، x ₂ ، ... ولكن بدلاً من أن تساوي 0 أو 1 ، يمكن أن يكون لهذه المدخلات أي قيمة في النطاق من 0 إلى 1. على سبيل المثال ، ستكون القيمة 0.638 مدخلات صالحة لـ الخلايا العصبية السيني (CH). تمامًا مثل perceptron ، لدى SN أوزان لكل إدخال ، w ₁ ، w ₂ ، ... والإنحياز الكلي b. لكن قيمة الخرج لن تكون 0 أو 1. وستكون σ (w⋅x + b) ، حيث σ هو السيني.

بالمناسبة ، sometimes تسمى أحيانًا دالة لوجستية ، وتسمى هذه الفئة من الخلايا العصبية بالخلايا العصبية اللوجستية. من المفيد أن نتذكر هذا المصطلح ، حيث يتم استخدام هذه المصطلحات من قبل العديد من الأشخاص الذين يعملون مع الشبكات العصبية. ومع ذلك ، فإننا سوف تلتزم المصطلحات السيني.

يتم تعريف الوظيفة على النحو التالي:

$$

$$\ sigma (z) \ equiv \ frac {1} {1 + e ^ {- z}} \ tag {3}$$

في حالتنا ، سيتم اعتبار قيمة الخرج للخلية العصبية السينية مع بيانات الإدخال x ₁ ، x ₂ ، ... بالأوزان w ₁ ، w ₂ ، ... والإزاحة b على النحو التالي:

$$

$$\ frac {1} {1 + exp (- \ sum_j w_jx_j - b)} \ العلامة {4}$$

للوهلة الأولى ، يبدو CH مختلفًا تمامًا عن الخلايا العصبية. قد تبدو النظرية الجبرية للسمك مربكة وغامضة إذا لم تكن معتادًا عليها. في الواقع ، هناك العديد من أوجه التشابه بين الإدراك الحسي و SN ، والشكل الجبري من السيني هو أكثر من التفاصيل الفنية من حاجز خطير لفهم.

لفهم أوجه التشابه في نموذج الإدراك الحسي ، افترض أن z ≡ w ⋅ x + b عدد موجب كبير. ثم e - z ≈ 0 ، لذلك ، σ (z) ≈ 1. بمعنى آخر ، عندما تكون z = w ⋅ x + b كبيرة وإيجابية ، فإن العائد SN يكون تقريبًا 1 ، كما في المدرك الخارجي. افترض أن z = w ⋅ x + b كبيرة مع علامة الطرح. ثم e - z → ∞ و σ (z) ≈ 0. لذلك بالنسبة إلى z الكبيرة ذات علامة الطرح ، يقترب سلوك SN أيضًا من الإدراك الحسي. وفقط عندما يكون متوسط ​​حجم w ⋅ x + b ، تكون هناك انحرافات خطيرة عن نموذج الإدراك الحسي.

ماذا عن الشكل الجبري لـ σ؟ كيف نفهمه؟ في الحقيقة ، الشكل الدقيق لـ not ليس مهمًا جدًا - شكل الوظيفة على الرسم البياني مهم. ومن هنا:



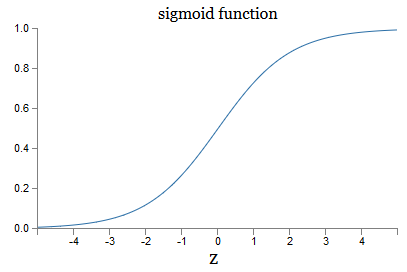
هذه نسخة سلسة من وظيفة الخطوة:



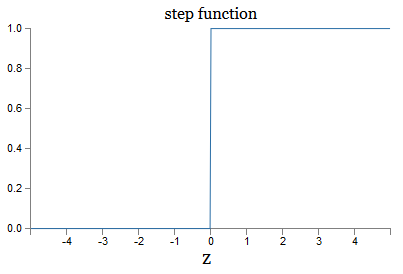
إذا كانت wise تدريجيًا ، فسيكون SN هو perceptron ، حيث سيكون له ناتج 0 أو 1 حسب الإشارة w ⋅ x + b (جيدًا ، في الواقع = z ، 0 يعطي perceptron 0 ، ووظيفة الخطوة 1 ، لذلك في هذه المرحلة ، يجب تغيير الوظيفة).

باستخدام الوظيفة الحقيقية σ ، نحصل على مدرك سلس. والشيء الرئيسي هنا هو سلاسة الوظيفة ، وليس شكلها الدقيق. نعومة يعني أن التغييرات الصغيرة - الأوزان _j و الإزاحة δb - سوف تعطي تغييرات صغيرة Δ إخراج الإخراج. يخبرنا الجبر أن الإخراج تقريبًا كما يلي:

$$

$$\ إخراج دلتا \ approx \ sum_j \ frac {\ إخراج جزئي} {\ جزئية w_j} \ دلتا w_j + \ frac {\ إخراج جزئي} {\ جزئي ب} \ دلتا ب \ علامة {5}$$

عندما يكون الجمع على كل الأوزان w _j ، و ∂output / ∂w _j و ∂output / ∂b تشير إلى المشتقات الجزئية للناتج بالنسبة إلى w _j و b ، على التوالي. لا داعي للذعر إذا كنت تشعر بعدم الأمان في شركة المشتقات الخاصة! على الرغم من أن الصيغة تبدو معقدة ، مع كل هذه المشتقات الجزئية ، فإنها تقول شيئًا بسيطًا جدًا (ومفيد): Δ الإخراج هو دالة خطية تعتمد على Δw _j و Δb الأوزان والتحيزات. الخطي يجعل من السهل تحديد التغييرات الصغيرة في الأوزان والإزاحة لتحقيق أي انحياز صغير في الإنتاج. لذلك ، على الرغم من تشابه SNS مع الإدراك الحسي في السلوك النوعي ، إلا أنها تسهل فهم كيفية تغيير المخرجات من خلال تغيير الأوزان والتشريد.

إذا كان الشكل العام important مهمًا بالنسبة لنا ، وليس لشكله الدقيق ، فلماذا نستخدم هذه الصيغة (3)؟ في الواقع ، سننظر لاحقًا في بعض الأحيان في الخلايا العصبية التي يكون ناتجها f (w ⋅ x + b) ، حيث f () هي بعض وظائف التنشيط الأخرى. الشيء الرئيسي الذي يتغير عندما تتغير الوظيفة هو قيمة المشتقات الجزئية في المعادلة (5). اتضح أنه عندما نقوم بعد ذلك بحساب هذه المشتقات الجزئية ، فإن استخدام σ يبسط بشكل كبير الجبر ، لأن الأس يكون له خصائص لطيفة للغاية عند التفريق. في أي حال ، يتم استخدام often غالبًا في العمل مع الشبكات العصبية ، وفي أغلب الأحيان في هذا الكتاب سنستخدم وظيفة التنشيط هذه.

كيف يمكن تفسير نتيجة عمل CH؟ من الواضح أن الاختلاف الرئيسي بين الإدراك الحسي و CH هو أن CH لا تعطي 0 أو 1 فقط. يمكن أن يكون ناتجها أي رقم حقيقي من 0 إلى 1 ، لذلك فإن القيم مثل 0.173 أو 0.689 صالحة. قد يكون ذلك مفيدًا ، على سبيل المثال ، إذا كنت بحاجة إلى قيمة الإخراج للإشارة ، على سبيل المثال ، إلى متوسط ​​سطوع وحدات البكسل للصورة التي تم تلقيها عند إدخال NS. لكن في بعض الأحيان يمكن أن يكون غير مريح. لنفترض أننا نريد أن يشير خرج الشبكة إلى أن "الصورة 9 كانت مدخلات" أو "صورة إدخال ليست 9". من الواضح ، سيكون من الأسهل إذا كانت قيم المخرجات 0 أو 1 ، مثل الإدراك الحسي. لكن في الممارسة العملية ، يمكننا أن نتفق على أن أي قيمة إخراج لا تقل عن 0.5 تعني "9" عند الإدخال ، وأي قيمة أقل من 0.5 تعني "لا 9". سأشير دائمًا إلى وجود مثل هذه الاتفاقيات.

تمارين

• CH محاكاة الإدراك الحسي ، الجزء 1

لنفترض أننا نأخذ جميع الأوزان والإزاحة من شبكة من الإدراك الحسي ، وضربها في ثابت موجب c> 0. تبين أن سلوك الشبكة لا يتغير.

• CH محاكاة الإدراك الحسي ، الجزء 2

لنفترض أن لدينا نفس الموقف كما في المشكلة السابقة - شبكة من الإدراك الحسي. لنفترض أيضًا تحديد بيانات الإدخال للشبكة. نحن لسنا بحاجة إلى قيمة محددة ، والشيء الرئيسي هو أنه ثابت. لنفترض أن الأوزان وعمليات الإزاحة تكون مثل w⋅x + b ≠ 0 ، حيث تمثل x قيمة إدخال أي مدرك في الشبكة. الآن نستبدل كل الإدراك الحسي في الشبكة بـ SN ، ونضرب الأوزان والتشريد بالثبات الموجب c> 0. أظهر أنه في الحد c → behavior سيكون سلوك الشبكة من الشبكة SN تمامًا مثل شبكات الإدراك الحسي. كيف سيتم انتهاك هذا البيان إذا كان أحد الإدراك الحسي w⋅x + b = 0؟

بنية الشبكة العصبية

في القسم التالي ، سأقدم شبكة عصبية قادرة على تصنيف جيد للأرقام المكتوبة بخط اليد. قبل ذلك ، من المفيد شرح المصطلحات التي تسمح لنا بالإشارة إلى أجزاء مختلفة من الشبكة. دعنا نقول لدينا الشبكة التالية:



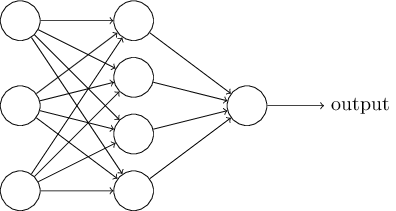
كما ذكرت ، فإن الطبقة الموجودة في أقصى اليسار في الشبكة تسمى طبقة الإدخال ، وتسمى الخلايا العصبية الخاصة بها بالخلايا العصبية المدخلة. تحتوي أقصى اليمين ، أو طبقة الإخراج ، على خلايا عصبية مخرجة ، أو ، كما في حالتنا ، عصبون مخرجات واحد. تسمى الطبقة الوسطى مخفية ، لأن خلاياها العصبية ليست مدخلات ولا مخرجات. قد يبدو المصطلح "مخفي" غامضًا بعض الشيء - عندما سمعت لأول مرة ، قررت أنه ينبغي أن يكون له بعض الأهمية الفلسفية أو الرياضية العميقة - ومع ذلك ، فهذا يعني فقط "عدم الدخول وليس الخروج". تحتوي الشبكة أعلاه على طبقة مخفية واحدة فقط ، ولكن تحتوي بعض الشبكات على عدة طبقات مخفية. على سبيل المثال ، يوجد في الشبكة الأربعة طبقات التالية طبقتان مخفيتان:



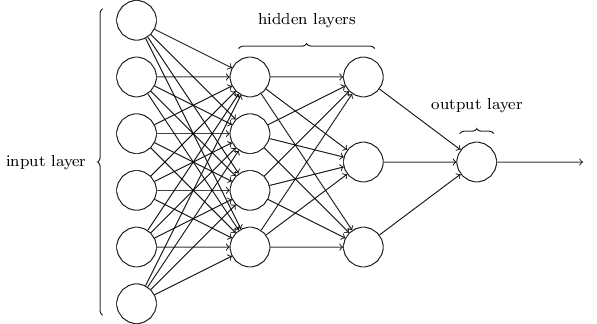
قد يكون هذا مربكًا ، ولكن لأسباب تاريخية ، تسمى هذه الشبكات متعددة الطبقات أحيانًا مدركات متعددة الطبقات ، MLPs ، على الرغم من أنها تتكون من عصبونات السيني بدلاً من الإدراك الحسي. لن أستخدم هذه المصطلحات لأنها مربكة ، لكن يجب أن أحذر من وجودها.

في بعض الأحيان يكون تصميم طبقات المدخلات والمخرجات مهمة بسيطة. على سبيل المثال ، دعنا نقول أننا نحاول تحديد ما إذا كان الرقم المكتوب بخط اليد يعني "9" أم لا. سوف ترمز دائرة الشبكة الطبيعية إلى سطوع وحدات بكسل الصورة في الخلايا العصبية المدخلة. إذا كانت الصورة بالأبيض والأسود ، بحجم 64 × 64 بكسل ، فسنحصل على 64 × 64 = 4096 خلية عصبية مدخلة ، مع سطوع في النطاق من 0 إلى 1. ستحتوي طبقة المخرجات على خلية عصبية واحدة فقط ، والتي تعني قيمتها أقل من 0.5 "على لم يكن الإدخال 9 "، ولكن القيم الأكبر ستعني أن" الإدخال كان 9 ".

في حين أن تصميم طبقات المدخلات والمخرجات غالبًا ما يكون مهمة بسيطة ، فإن تصميم الطبقات المخفية يمكن أن يكون عملية صعبة. على وجه الخصوص ، لا يمكن وصف عملية تطوير الطبقات المخفية ببعض القواعد البسيطة. طور باحثو الجمعية الوطنية العديد من القواعد الإرشادية لتصميم الطبقات المخفية التي تساعد على الحصول على السلوك المرغوب للشبكات العصبية. على سبيل المثال ، يمكن استخدام مثل هذا الكشف عن مجريات الأمور لفهم كيفية تحقيق حل وسط بين عدد الطبقات المخفية والوقت المتاح لتدريب الشبكة. في وقت لاحق سنواجه بعض هذه القواعد.

لقد ناقشنا حتى الآن NSs التي يتم فيها استخدام ناتج طبقة واحدة كمدخلات للمادة التالية. وتسمى هذه الشبكات شبكات التوزيع العصبي المباشر. هذا يعني أنه لا توجد حلقات في الشبكة - فالمعلومات تمضي دائمًا إلى الأمام ولا تتغذى أبدًا. إذا كانت لدينا حلقات ، فسنواجه مواقف يعتمد فيها السيني المخفي على المخرجات. سيكون من الصعب فهم ذلك ، ونحن لا نسمح بمثل هذه الحلقات.

ومع ذلك ، هناك نماذج أخرى من NSs الاصطناعية التي من الممكن استخدام حلقات التعليق. وتسمى هذه النماذج الشبكات العصبية المتكررة (RNS). فكرة هذه الشبكات هي أن الخلايا العصبية الخاصة بهم يتم تنشيطها لفترات زمنية محدودة. يمكن لهذا التنشيط أن يحفز النيوترونات الأخرى ، التي يمكن تنشيطها لاحقًا ، لفترة محدودة أيضًا. يؤدي ذلك إلى تنشيط الخلايا العصبية التالية ، ومع مرور الوقت نحصل على سلسلة من الخلايا العصبية المنشطة. لا تمثل الحلقات في مثل هذه النماذج مشكلات ، لأن إخراج الخلايا العصبية يؤثر على دخولها في وقت لاحق ، وليس على الفور.

لم تكن RNSs مؤثرة مثل NS من التوزيع المباشر ، ولا سيما لأن خوارزميات التدريب لـ RNSs لديها حتى الآن إمكانات أقل. ومع ذلك ، لا يزال RNS مثيرة للاهتمام للغاية. وبروح العمل ، فإنهم أقرب إلى الدماغ من NS للتوزيع المباشر. من الممكن أن يكون RNS قادرًا على حل المشكلات المهمة التي يمكن حلها بصعوبات كبيرة بمساعدة التوزيع المباشر NS. ومع ذلك ، من أجل الحد من نطاق دراستنا ، سوف نركز على NS الأكثر استخدامًا للتوزيع المباشر.

شبكة تصنيف الحبر بسيطة

بعد تحديد الشبكات العصبية ، سنعود إلى التعرف على خط اليد. يمكن تقسيم مهمة التعرف على الأرقام المكتوبة بخط اليد إلى مهمتين فرعيتين. أولاً ، نريد أن نجد طريقة لتقسيم صورة تحتوي على العديد من الأرقام إلى سلسلة من الصور الفردية ، يحتوي كل منها على رقم واحد. على سبيل المثال ، نود تقسيم الصورة



إلى ستة منفصلة



يمكننا نحن البشر بسهولة حل مشكلة التجزئة ، لكن يصعب على برنامج الكمبيوتر تقسيم الصورة بشكل صحيح. بعد التجزئة ، يحتاج البرنامج إلى تصنيف كل رقم على حدة. لذلك ، على سبيل المثال ، نريد أن يتعرف برنامجنا على الرقم الأول



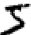
إنه 5.

سوف نركز على إنشاء برنامج لحل المشكلة الثانية ، تصنيف الأرقام الفردية. اتضح أن مشكلة التجزئة ليست صعبة للغاية بمجرد إيجاد طريقة جيدة لتصنيف الأرقام الفردية. هناك العديد من الطرق لحل مشكلة التجزئة. أحدها هو تجربة العديد من الطرق المختلفة لتقسيم الصور باستخدام مصنف الأرقام الفردية ، وتقييم كل محاولة. تحظى التقسيم التجريبي بتقدير كبير إذا كان مصنف الأرقام الفردية واثقًا من تصنيف جميع القطاعات ، وكان منخفضًا إذا كان لديه مشاكل في جزء واحد أو أكثر. الفكرة هي أنه إذا واجه المصنف مشاكل في مكان ما ، فهذا على الأرجح يعني أن التجزئة غير صحيحة. يمكن استخدام هذه الفكرة والخيارات الأخرى لحل جيد لمشكلة التجزئة. لذا ، بدلاً من القلق بشأن التجزئة ، سنركز على تطوير NS قادر على حل مهمة أكثر تشويقًا وتعقيدًا ، أي التعرف على الأرقام المكتوبة بخط اليد الفردية.

للتعرف على الأرقام الفردية ، سنستخدم NS من ثلاث طبقات:



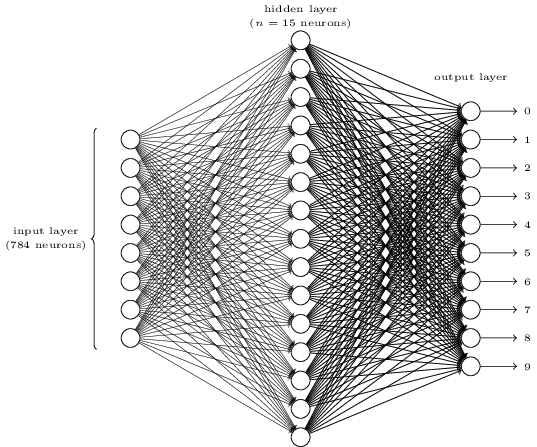
تحتوي طبقة شبكة الإدخال على خلايا عصبية تقوم بترميز قيم مختلفة من وحدات بكسل الإدخال. كما هو موضح في القسم التالي ، ستتألف بيانات التدريب الخاصة بنا من العديد من الصور للأرقام المكتوبة بخط اليد الممسوحة ضوئيًا بحجم 28 × 28 بكسل ، لذلك تحتوي طبقة الإدخال على 28 × 28 = 784 خلية عصبية. للبساطة ، أنا لم أشير إلى معظم الخلايا العصبية 784 في الرسم البياني. البيكسلات الواردة بالأبيض والأسود ، بقيمة 0.0 تشير إلى الأبيض ، 1.0 تشير إلى الأسود ، والقيم الوسيطة تشير إلى ظلال رمادية داكنة.

الطبقة الثانية من الشبكة مخفية. نشير إلى عدد الخلايا العصبية في هذه الطبقة n ، وسنقوم بتجربة قيم مختلفة من n. يوضح المثال أعلاه طبقة مخفية صغيرة تحتوي فقط على 15 خلية عصبية.

هناك 10 الخلايا العصبية في طبقة الإخراج للشبكة. إذا تم تنشيط الخلية العصبية الأولى ، أي أن قيمة الخرج هي ≈ 1 ، فهذا يشير إلى أن الشبكة تعتقد أن الإدخال كان 0. إذا تم تنشيط الخلية العصبية الثانية ، تعتقد الشبكة أن الإدخال كان 1. وهكذا. بالمعنى الدقيق للكلمة ، نحن نرقم الخلايا العصبية الناتجة من 0 إلى 9 ، وننظر إلى أي منهم لديه أقصى قيمة التنشيط. إذا كانت هذه ، على سبيل المثال ، الخلايا العصبية رقم 6 ، فإن شبكتنا تعتقد أن الإدخال كان رقم 6. وهكذا.

قد تتساءل لماذا نحتاج إلى استخدام عشرة خلايا عصبية. بعد كل شيء ، نريد أن نعرف أي رقم من 0 إلى 9 يتوافق مع صورة الإدخال. سيكون من الطبيعي استخدام 4 خلايا عصبية فقط ، كل واحدة منها ستأخذ قيمة ثنائية ، اعتمادًا على ما إذا كانت قيمة الخرج أقرب إلى 0 أو 1. ستكون أربعة خلايا عصبية كافية ، لأن 2 ⁴ = 16 ، أكثر من 10 قيم ممكنة. لماذا يجب أن تستخدم شبكتنا 10 خلايا عصبية؟ هل هذا غير فعال؟ أساس هذا هو تجريبي. يمكننا تجربة كلا الخيارين في الشبكة ، وتبين أنه بالنسبة لهذه المهمة ، يتم تدريب شبكة تضم 10 خلايا عصبية مخرجات بشكل أفضل على التعرف على الأرقام مقارنة بالشبكة التي تحتوي على 4. ومع ذلك ، يبقى السؤال ، لماذا يتم تحسين الخلايا العصبية 10 الإخراج. هل هناك أي ارشادي من شأنه أن يخبرنا مقدما أنه ينبغي استخدام 10 الخلايا العصبية الإخراج بدلا من 4؟

لفهم السبب ، من المفيد التفكير فيما تفعله الشبكة العصبية. أولا ، النظر في الخيار مع 10 الخلايا العصبية الإخراج. نحن نركز على أول خلية عصبية الإخراج ، والتي تحاول أن تقرر ما إذا كانت الصورة الواردة هي صفر. يفعل هذا من خلال وزن الأدلة التي تم الحصول عليها من طبقة مخفية. ماذا الخلايا العصبية الخفية تفعل؟ لنفترض أن العصبون الأول في الطبقة المخفية يحدد ما إذا كان هناك شيء مثل هذا في الصورة:



يمكنه القيام بذلك عن طريق تعيين أوزان كبيرة للبكسل المطابقة لهذه الصورة ، والأوزان الصغيرة للباقي. بنفس الطريقة ، افترض أن الخلايا العصبية الثانية والثالثة والرابعة في الطبقة المخفية تبحث عن وجود شظايا متشابهة في الصورة:



كما قد تكون خمنت ، فإن هذه الأجزاء الأربعة مجتمعة تعطي الصورة 0 ، والتي رأيناها سابقًا:



لذلك ، إذا تم تنشيط الخلايا العصبية الأربعة المخفية ، يمكننا أن نستنتج أن الرقم هو 0. بالطبع ، ليس هذا هو الدليل الوحيد على أن 0 عُرض هناك - يمكننا الحصول على 0 بعدة طرق أخرى (عن طريق تحوير هذه الصور قليلاً أو تشويهها قليلاً). ومع ذلك ، يمكننا القول بالتأكيد ، على الأقل في هذه الحالة ، يمكننا أن نستنتج أنه كان هناك 0 في الإدخال.

إذا افترضنا أن الشبكة تعمل على هذا النحو ، فيمكننا تقديم تفسير معقول لماذا من الأفضل استخدام 10 خلايا عصبية مخرجات بدلاً من 4. إذا كان لدينا 4 خلايا عصبية مخرجة ، عندها ستحاول العصبون الأول تحديد ما هو الجزء الأكثر أهمية من الرقم الوارد. وليس هناك طريقة سهلة لربط الشيء الأكثر أهمية بالنماذج البسيطة المذكورة أعلاه. من الصعب تخيل أي أسباب تاريخية لارتباط أجزاء من شكل الأرقام بطريقة أو بأخرى بالجزء الأكثر أهمية من المخرجات.

ومع ذلك ، كل ما سبق مدعوم فقط من قبل الاستدلال. لا شيء يتحدث عن حقيقة أن شبكة ثلاثية الطبقات يجب أن تعمل كما قلت ، وينبغي أن تجد الخلايا العصبية المخفية مكونات بسيطة من الأشكال. ربما ستجد خوارزمية التعلم الصعبة بعض الأوزان التي تسمح لنا باستخدام 4 خلايا عصبية فقط. ومع ذلك ، كطريقة ارشادية ، فإن طريقتي تعمل بشكل جيد ، ويمكن أن توفر لك وقتًا طويلاً في تطوير بنية NS جيدة.

تمارين

• , . , . . , 3 , ( ) 0,99, 0,01.

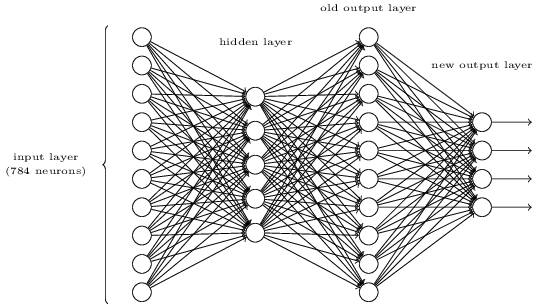لذلك ، لدينا مخطط NA - كيفية تعلم كيفية التعرف على الأرقام؟ أول شيء نحتاجه هو بيانات التدريب ، ما يسمى مجموعة بيانات التدريب. سوف نستخدم مجموعة من MNIST ، تحتوي على عشرات الآلاف من الصور الممسوحة ضوئيا من الأرقام المكتوبة بخط اليد، وتصنيفها الصحيح. الاسم الذي تلقاه MNIST نظرًا لأنه مجموعة فرعية معدلة من مجموعتي البيانات المجمعتين بواسطة NIST ، المعهد الوطني الأمريكي للمعايير والتكنولوجيا. فيما يلي بعض الصور من MNIST:



هذه هي نفس الأرقام التي تم تقديمها في بداية الفصل كمهمة التعرف. بالطبع ، عند التحقق من NS ، سنطلب منها التعرف على الصور الخاطئة التي كانت موجودة بالفعل في مجموعة التدريب!

تتكون بيانات MNIST من جزأين. الأول يحتوي على 60000 صورة مخصصة للتدريب. هذه المخطوطات الممسوحة ضوئيًا من 250 شخصًا ، نصفهم من موظفي مكتب الإحصاء الأمريكي ، والنصف الآخر من طلاب المدارس الثانوية. الصور بالأبيض والأسود ، بقياس 28 × 28 بكسل. الجزء الثاني من مجموعة البيانات MNIST هو 10000 صورة لاختبار الشبكة. هذا أيضًا صورة أبيض وأسود 28 × 28 بكسل. سنستخدم هذه البيانات لتقييم مدى معرفة الشبكة بالتعرف على الأرقام. لتحسين جودة التقييم ، تم أخذ هذه الأرقام من 250 شخصًا آخر لم يشاركوا في تسجيل مجموعة التدريب (على الرغم من أنهم كانوا أيضًا موظفين في المكتب وطلاب المدارس الثانوية). يساعدنا ذلك في التأكد من أن نظامنا يمكنه التعرف على خط اليد للأشخاص الذين لم يلتقوا به أثناء التدريب.

سيتم الإشارة إلى إدخال التدريب بواسطة x. سيكون من المناسب التعامل مع كل صورة إدخال x كمتجه مع قياس 28x28 = 784. تشير كل قيمة داخل المتجه إلى سطوع بكسل واحد في الصورة. سنشير إلى قيمة الخرج كـ y = y (x) ، حيث y عبارة عن ناقل أحادي الأبعاد. على سبيل المثال ، إذا كانت صورة التدريب x المحددة تحتوي على 6 ، فإن y (x) = (0،0،0،0،0،0،1،0،0) ستكون ^T هي المتجه الذي نحتاج إليه. T هي عملية تبديل تحول متجه الصف إلى متجه عمود.

نريد العثور على خوارزمية تسمح لنا بالبحث عن هذه الأوزان والإزاحة بحيث يقترب ناتج الشبكة من y (x) لجميع مدخلات التدريب x. لتحديد تقريب هذا الهدف ، نحدد دالة تكلفة (تسمى أحيانًا دالة الخسارة. في الكتاب سوف نستخدم دالة التكلفة ، ولكن تذكر اسمًا آخر):

$$

$$C(w, b) = \frac{1}{2n} \sum_x || y(x) – a ||^2 \tag{6}$$

هنا تشير w إلى مجموعة من أوزان الشبكة ، b عبارة عن مجموعة من الإزاحات ، n هو عدد بيانات إدخال التدريب ، وهي متجه لبيانات المخرجات عندما تكون x عبارة عن بيانات إدخال ، ويمر المجموع عبر جميع مدخلات التدريب x. المخرجات ، بالطبع ، تعتمد على x ، w و b ، لكن من أجل البساطة لم أسمي هذا الاعتماد. التدوين || v || يعني طول المتجه الخامس. سوف نسمي C دالة تكلفة تربيعية ؛ في بعض الأحيان يطلق عليه أيضا الخطأ القياسي ، أو MSE. إذا نظرت عن كثب إلى C ، يمكنك أن ترى أنه ليس سلبًا ، لأن جميع أعضاء المجموع غير سالب. بالإضافة إلى ذلك ، تصبح تكلفة C (w ، b) صغيرة ، أي C (w ، b) ≈ 0 ، على وجه التحديد عندما تكون y (x) مساوية تقريبًا لمتجه الإخراج a لجميع بيانات إدخال التدريب x. لذلك خوارزمية لدينا عملت بشكل جيد إذا تمكنا من العثور على الأوزان والإزاحة مثل C (ث ، ب) ≈ 0. والعكس ، كان يعمل بشكل سيء عندما C (ث ،ب) كبير - وهذا يعني أن y (x) لا تتطابق مع الإخراج لكمية كبيرة من المدخلات. اتضح أن الهدف من خوارزمية التدريب هو تقليل تكلفة C (w ، b) كدالة للأوزان والإزاحة. بمعنى آخر ، نحن بحاجة إلى إيجاد مجموعة من الأوزان والإزاحة التي تقلل من قيمة التكلفة. سنفعل ذلك باستخدام خوارزمية تسمى النسب التدرج.

لماذا نحتاج إلى قيمة من الدرجة الثانية؟ ألا يهمنا بشكل أساسي عدد الصور التي تم التعرف عليها بشكل صحيح من قبل الشبكة؟ هل من الممكن ببساطة زيادة هذا الرقم إلى الحد الأقصى بشكل مباشر ، وليس تقليل القيمة الوسيطة للقيمة التربيعية إلى الحد الأدنى؟ المشكلة هي أن عدد الصور التي تم التعرف عليها بشكل صحيح ليس وظيفة سلسة لأوزان وإزاحات الشبكة. بالنسبة للجزء الأكبر ، لن تغير التغييرات الصغيرة في الأوزان والإزاحة عدد الصور المعترف بها بشكل صحيح. لهذا السبب ، من الصعب فهم كيفية تغيير الأوزان والتحيزات لتحسين الكفاءة. إذا استخدمنا دالة تكلفة سلسة ، فسيكون من السهل علينا فهم كيفية إجراء تغييرات صغيرة في الأوزان والإزاحة من أجل تحسين التكلفة. لذلك ، سوف نركز أولاً على القيمة التربيعية ، ومن ثم سنبحث دقة التصنيف.

حتى لو أخذنا في الاعتبار أننا نرغب في استخدام دالة تكلفة سلسة ، فقد تظل مهتمًا لماذا اخترنا الدالة التربيعية للمعادلة (6)؟ أليس من الممكن اختياره بشكل تعسفي؟ ربما إذا اخترنا وظيفة مختلفة ، فسنحصل على مجموعة مختلفة تمامًا من تقليل الأوزان والإزاحة؟ سؤال معقول ، وبعد ذلك سنقوم مرة أخرى بفحص وظيفة التكلفة وإجراء بعض التصحيحات لها. ومع ذلك ، فإن وظيفة التكلفة التربيعية تعمل بشكل جيد لفهم الأشياء الأساسية في تعلم NS ، لذلك سنلتزم بها حتى الآن.

لتلخيص: هدفنا في تدريب NS هو إيجاد الأوزان والإزاحة التي تقلل من وظيفة التكلفة التربيعية C (w ، b). تم طرح المهمة بشكل جيد ، لكن لديها حتى الآن العديد من الهياكل المُشتتة - تفسير w و b كأوزان وإزاحة ، الوظيفة - مخفية في الخلفية ، واختيار بنية الشبكة ، MNIST ، وما إلى ذلك. اتضح أنه يمكننا فهم الكثير ، وتجاهل معظم هذا الهيكل ، والتركيز فقط على جانب التقليل. حتى الآن ، سوف ننسى الشكل الخاص لوظيفة التكلفة ، والتواصل مع الجمعية الوطنية ، وهلم جرا. بدلاً من ذلك ، سوف نتخيل أن لدينا فقط وظيفة بها العديد من المتغيرات ، ونريد تقليلها. سنقوم بتطوير تقنية تسمى النسب التدرج ، والتي يمكن استخدامها لحل مثل هذه المشاكل. ثم عدنا إلى وظيفة معينة ،الذي نريد تقليله للجمعية الوطنية.

حسنًا ، دعنا نقول أننا نحاول تقليل بعض الوظائف C (v). يمكن أن تكون أي وظيفة ذات قيم حقيقية للعديد من المتغيرات v = v ₁ ، v ₂ ، ... لاحظ أنني قمت باستبدال الترميز w و b بـ v لإظهار أنه يمكن أن يكون أي وظيفة - لم نعد مهووسين بالـ HC. من المفيد أن نتخيل أن الدالة C لها متغيرين فقط - v ₁ و v ₂ :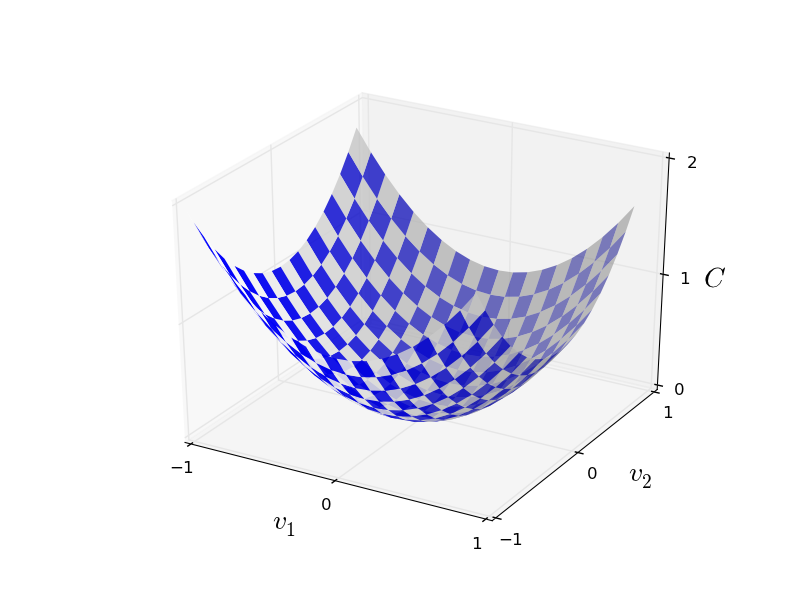



نود أن نجد حيث تصل C إلى الحد الأدنى العام. بالطبع ، من خلال الوظيفة الموضحة أعلاه ، يمكننا دراسة الرسم البياني والعثور على الحد الأدنى. بهذا المعنى ، ربما أعطيتك وظيفة بسيطة للغاية! في الحالة العامة ، يمكن أن تكون C دالة معقدة للعديد من المتغيرات ، وعادة ما يكون من المستحيل إلقاء نظرة على الرسم البياني والعثور على الحد الأدنى.

طريقة واحدة لحل المشكلة هي استخدام الجبر للعثور على الحد الأدنى من الناحية التحليلية. يمكننا حساب المشتقات ومحاولة استخدامها للعثور على الحد الأقصى. إذا كنا محظوظين ، فسيتم ذلك عندما تكون C دالة لمتغير واحد أو اثنين. لكن مع وجود عدد كبير من المتغيرات ، يتحول هذا إلى كابوس. وبالنسبة إلى NS ، نحتاج غالبًا إلى المزيد من المتغيرات - بالنسبة لأكبر NS ، تعتمد وظائف التكلفة بطريقة معقدة على مليارات الأوزان والتشريد. باستخدام الجبر لتقليل هذه الوظائف سوف تفشل!

(بعد أن أوضحت أنه سيكون من الأنسب بالنسبة لنا أن نعتبر C كدالة لمتغيرين ، قلت مرتين في فقرتين "نعم ، ولكن ماذا لو كانت دالة لعدد أكبر بكثير من المتغيرات؟" أعتذر. صدقنا ، سيكون من المفيد بالنسبة لنا تمثيل C كدالة اثنين من المتغيرات ، هو أنه في بعض الأحيان تنهار هذه الصورة ، وهذا هو السبب في الحاجة إلى الفقرتين السابقتين ، ولأغراض التفكير الرياضي غالباً ما يكون من الضروري التوفيق بين عدة عروض بديهية ، والتعلم في الوقت نفسه عندما يمكن استخدام التمثيل وعندما لا zya).

حسنًا ، هذا يعني أن الجبر لن ينجح. لحسن الحظ ، هناك تشابه كبير يوفر خوارزمية جيدة الأداء. نحن نتخيل وظيفتنا كشيء مثل الوادي. مع الجدول الزمني الأخير ، لن يكون من الصعب القيام به. ونتخيل كرة تدور على طول منحدر الوادي. تخبرنا تجربتنا أن الكرة سوف تنزلق في النهاية إلى أسفلها. ربما يمكننا استخدام هذه الفكرة للعثور على الحد الأدنى من وظيفة؟ نختار بشكل عشوائي نقطة الانطلاق لكرات خيالية ، ومن ثم محاكاة حركة الكرة ، كما لو كانت تتدحرج إلى قاع الوادي. يمكننا استخدام هذه المحاكاة ببساطة عن طريق حساب المشتقات (وربما المشتقات الثانية) من C - سيخبروننا كل شيء عن الشكل المحلي للوادي ، وبالتالي حول كيفية لفة الكرة لدينا.

بناءً على ما كتبته ، قد تظن أننا سنكتب معادلات نيوتن للحركة للكرة ، وننظر في آثار الاحتكاك والجاذبية ، وما إلى ذلك. في الواقع ، لن نكون قريبين جدًا من اتباع هذا التشبيه بالكرة - نحن نعمل على تطوير خوارزمية لتقليل C ، وليس محاكاة دقيقة لقوانين الفيزياء! يجب أن يحفز هذا التشبيه خيالنا ، ولا يحد من تفكيرنا. لذا ، بدلاً من الغوص في التفاصيل المعقدة للفيزياء ، دعنا نطرح السؤال التالي: إذا تم تعييننا إلهًا ليوم واحد ، وسننشئ قوانيننا الخاصة بالفيزياء ، ونخبر الكرة كيف يتم تطبيق القانون أو قوانين الحركة التي سنختارها ، بحيث تتدحرج الكرة دائمًا قاع الوادي؟

لتوضيح المشكلة ، سنفكر فيما يحدث إذا حركنا الكرة لمسافة صغيرة - ₁ في اتجاه v ₁، ومسافة صغيرة Δv ₂ في اتجاه v ₂ . يخبرنا الجبر أن C يتغير كما يلي:

$$

$$\Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2 \tag{7}$$

سنجد طريقة لاختيار مثل suchv ₁ و 2v ₂ بحيث تكون ΔC أقل من الصفر ؛ أي أننا سنختارهم حتى تدور الكرة. لفهم كيفية القيام بذلك ، من المفيد تعريف Δv على أنها متجه التغييرات ، أي Δv ≡ (Δv ₁ ، Δv ₂ ) ^T ، حيث T هي عملية التحويل التي تحول متجهات الصف إلى متجهات أعمدة. نحن أيضا تحديد ناقلات التدرج C كما المشتقات الجزئية (∂S / ∂v ₁ ، ∂S / ∂v ₂ ) ^T . نشير إلى متجه التدرج بواسطة ∇:

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2})^T \tag{8}$$

سنقوم قريبًا بإعادة كتابة التغيير في درجة الحرارة من throughC إلى Δv والتدرج ∇C. في هذه الأثناء ، أريد توضيح شيء ما بسبب تعليق الناس في التدرج اللوني. عندما التقوا للمرة الأولى بـ "درجة مئوية" ، لا يفهم الناس في بعض الأحيان كيف ينبغي أن يتصوروا الرمز ∇. ماذا يعني بالتحديد؟ في الواقع ، يمكنك أن تأخذ بأمان ∇C كائنًا رياضيًا واحدًا - متجهًا محددًا مسبقًا - والذي تتم كتابته ببساطة باستخدام حرفين. من وجهة النظر هذه ، like يشبه التلويح بالعلم الذي يبلغ أن "∇C عبارة عن ناقل متدرج." هناك وجهات نظر أكثر تقدماً والتي يمكن اعتبار ∇ أنها كيان رياضي مستقل (على سبيل المثال ، كمشغل للتمايز) ، لكننا لسنا بحاجة إليها.

باستخدام مثل هذه التعريفات ، يمكن إعادة كتابة التعبير (7) على النحو التالي:

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{9}$$

تساعد هذه المعادلة على توضيح سبب تسمية ∇C لمتجه التدرج: فهي تربط التغييرات في v بالتغييرات في C ، كما هو متوقع من كيان يسمى التدرج اللوني. [المهندس. التدرج - الانحراف / تقريبا. ترجمة.] ومع ذلك ، من المثير للاهتمام أن هذه المعادلة تسمح لنا برؤية كيفية اختيار Δv بحيث تكون C سالبة. دعنا نقول نختار

$$

$$\Delta v = - \eta \nabla C \tag{10}$$

حيث η معلمة إيجابية صغيرة (سرعة التعلم). ثم تخبرنا المعادلة (9) أن ΔC ≈ - η ∇C ⋅ ∇C = - η || ∇C || ² . منذ || ∇C || ² ≥ 0 ، وهذا يضمن أن ΔC ≤ 0 ، بمعنى ، C ستنخفض طوال الوقت إذا قمنا بتغيير v ، كما هو موصوف في (10) (بالطبع ، كجزء من التقريب من المعادلة (9)). وهذا هو بالضبط ما نحتاجه! لذلك ، نأخذ المعادلة (10) لتحديد "قانون الحركة" للكرة في خوارزمية نزول التدرج لدينا. بمعنى ، سوف نستخدم المعادلة (10) لحساب قيمة Δv ، ثم سننقل الكرة إلى هذه القيمة:

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{11}$$

ثم نطبق هذه القاعدة مرة أخرى على الخطوة التالية. مواصلة التكرار ، سوف نخفض C حتى نأمل أن نصل إلى الحد الأدنى العالمي.

باختصار ، يعمل نزول التدرج من خلال حساب متتابع للتدرج C ، والإزاحة اللاحقة في الاتجاه المعاكس ، مما يؤدي إلى "السقوط" على طول منحدر الوادي. يمكن تصور ذلك على النحو التالي: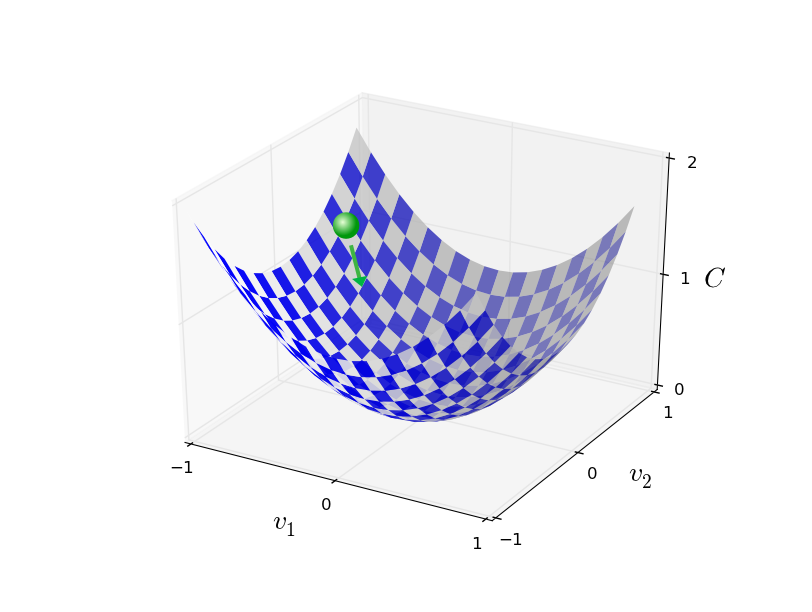



لاحظ أنه مع هذه القاعدة ، لا ينحدر التدرج اللوني حركة جسدية حقيقية. في الحياة الواقعية ، تتمتع الكرة بدافع يمكن أن يسمح لها بالتدحرج عبر المنحدر ، أو حتى التمدد لبعض الوقت. فقط بعد عمل قوة الاحتكاك تكون الكرة مضمونة لتدوير الوادي. تقول قاعدة الاختيار الخاصة بنا "نزول". قاعدة جيدة للعثور على الحد الأدنى!

لكي يعمل انحدار التدرج بشكل صحيح ، نحتاج إلى اختيار قيمة صغيرة بما يكفي لسرعة التعلم η بحيث تكون المعادلة (9) تقريبية جيدة. خلاف ذلك ، قد يتضح أن ΔC> 0 - لا شيء جيد! في الوقت نفسه ، ليس من الضروري أن تكون صغيرة جدًا ، حيث أن التغييرات في v ستكون صغيرة جدًا ، وستعمل الخوارزمية ببطء شديد. في الممارسة العملية ، تتغير η بحيث تعطي المعادلة (9) تقريبًا جيدًا ، والخوارزمية لا تعمل ببطء شديد. في وقت لاحق سوف نرى كيف يعمل.

شرحت نزول التدرج عندما تعتمد الدالة C على متغيرين فقط. لكن كل شيء يعمل بالطريقة نفسها إذا كانت C هي دالة للعديد من المتغيرات. لنفترض أن لديها متغيرات m ، v ₁ ، ... ، v _m. ثم التغيير في ΔC الناتج عن تغيير بسيط في Δv = (Δv ₁ ، ... ، mv _m ) ^T سيكون

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{12}$$

حيث التدرج ∇C هو المتجه

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1},…, \frac{\partial C}{\partial v_m})^T \tag{13}$$

كما هو الحال مع اثنين من المتغيرات ، يمكننا اختيار

$$

$$\Delta v = - \eta \nabla C \tag{14}$$

وتأكد من أن تعبيرنا التقريبي (12) لـ ΔC سالب. يمنحنا ذلك طريقة للالتفاف على التدرج اللوني إلى الحد الأدنى ، حتى عندما تكون C دالة للعديد من المتغيرات ، مع تطبيق قاعدة التحديث مرارًا وتكرارًا.

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{15}$$

يمكن اعتبار قاعدة التحديث هذه خوارزمية تحديد تدرج النسب. إنها تعطينا طريقة لتغيير موضع v بشكل متكرر بحثًا عن الحد الأدنى من الوظيفة C. لا تعمل هذه القاعدة دائمًا - قد تسوء عدة أشياء ، وتمنع نزول التدرج من إيجاد الحد الأدنى العام لـ C - سنعود إلى هذه النقطة في الفصول التالية. ولكن في الممارسة العملية ، يعمل نزول التدرج في كثير من الأحيان بشكل جيد للغاية ، وسوف نرى أنه في الجمعية الوطنية هذه طريقة فعالة لتقليل وظيفة التكلفة ، وبالتالي تدريب الشبكة.

بمعنى ما ، يمكن اعتبار نزول التدرج هو أفضل استراتيجية بحث الحد الأدنى. لنفترض أننا نحاول نقل Δv إلى موضع لتقليل C. هذا معادل لتقليل ΔC ≈ ∇C ⋅ Δv. سنحدد حجم الخطوة بحيث || Δv || = ε بالنسبة لبعض ثابت صغير ε> 0. وبعبارة أخرى ، نريد أن نحرك مسافة صغيرة من حجم ثابت ، ومحاولة العثور على اتجاه الحركة التي تنخفض C أكبر قدر ممكن. يمكن إثبات أن اختيار Δv تصغير ∇C ⋅ Δv هو Δv = -η∇C ، حيث يتم تحديد η = ε / || ∇C || بالقيود || Δv || = ε. لذلك يمكن اعتبار نزول التدرج وسيلة لاتخاذ خطوات صغيرة في الاتجاه الذي ينقص C. معظم.

تمارين

• . : — , , , .
• , , . , ? ?

لقد درس الناس العديد من الخيارات للنسب المتدرج ، بما في ذلك الخيارات التي تنتج بدقة أكثر كرة جسدية حقيقية. تتمتع هذه الخيارات بمزاياها ، ولكن أيضًا بها عيبًا كبيرًا: الحاجة إلى حساب المشتقات الجزئية الثانية من C ، والتي يمكن أن تستهلك الكثير من الموارد. لفهم هذا ، افترض أننا بحاجة إلى حساب جميع المشتقات الجزئية الثانية ∂ ² C / ∂v _j ∂v _k . إذا كانت المتغيرات v _{j هي} مليون ، فسنحتاج إلى حساب حوالي تريليون (مليون تربيع) من المشتقات الجزئية الثانية (في الواقع ، نصف تريليون ، منذ C ² C / ∂v _j ∂v _k = ∂ ² C / ∂v _k ∂v _j. لكنك اشتعلت الجوهر). هذا سوف يتطلب الكثير من موارد الحوسبة. هناك حيل لتجنب ذلك ، والبحث عن بدائل للنسب المتدرج مجال للبحث النشط. ومع ذلك ، في هذا الكتاب ، سوف نستخدم النسب المتدرج ومتغيراته كنهج رئيسي لتعلم NS.

كيف يمكننا تطبيق النسب التدرج على التعلم NA؟ نحتاج إلى استخدامه للبحث عن الأوزان w _k والإزاحة b _l التي تقلل من معادلة التكلفة (6). دعنا نعيد كتابة قاعدة تحديث النسب المتدرجة من خلال استبدال المتغيرات v _j بالأوزان _{والإزاحة} . بمعنى آخر ، "موقفنا" يحتوي الآن على المكونات w _k و b _l ، ويحتوي متجه التدرج ∇C على المكونات المقابلة ∂C / ∂w_k و /C / lb _l . بعد كتابة قاعدة التحديث الخاصة بنا بمكونات جديدة ، نحصل على:

$$

$$w_k \rightarrow w'_k = w_k - \eta \frac{\partial C}{\partial w_k} \tag{16}$$

$$

$$b_l \rightarrow b'_l = b_l - \eta \frac{\partial C}{\partial b_l} \tag{17}$$

من خلال إعادة تطبيق قاعدة التحديث هذه ، يمكننا "التراجع" ، ومع أي حظ ، نجد الحد الأدنى من تكلفة الوظيفة. بمعنى آخر ، يمكن استخدام هذه القاعدة لتدريب الجمعية الوطنية.

هناك العديد من العقبات التي تحول دون تطبيق قاعدة النسب التدرج. سوف ندرسهم بمزيد من التفصيل في الفصول التالية. لكن الآن ، أود أن أذكر مشكلة واحدة فقط. لفهمها ، دعنا نعود إلى القيمة التربيعية في المعادلة (6). لاحظ أن دالة التكلفة هذه تشبه C = 1 / n ∑ _x C _x ، وهذا هو ، متوسط ​​التكلفة C _x ≡ (|| y (x) −a || ² ) / 2 للحصول على أمثلة تدريب فردية. في الممارسة العملية ، لحساب التدرج المجهري ، نحتاج إلى حساب التدرجات المئوية _xبشكل منفصل لكل إدخال تدريب x ، ثم متوسط ​​لهم ، ∇C = 1 / n ∑ _x ∇C _x . لسوء الحظ ، عندما تكون كمية المدخلات كبيرة جدًا ، سيستغرق الأمر وقتًا طويلاً للغاية ، وسيكون هذا التدريب بطيئًا.

لتسريع التعلم ، يمكنك استخدام النسب التدرج العشوائي. الفكرة هي حساب تدرج approximatelyC تقريبًا عن طريق حساب ∇C _x لعينة عشوائية صغيرة من مدخلات التدريب. من خلال حساب المتوسط ​​، يمكننا الحصول بسرعة على تقدير جيد للتدرج الحقيقي trueC ، وهذا يساعد على تسريع نزول التدرج ، وبالتالي التدريب.

صياغة بشكل أكثر دقة ، يعمل النسب التدرج العشوائي العشوائي من خلال أخذ عينات عشوائية من عدد صغير من بيانات إدخال التدريب م. سوف نسمي هذه البيانات العشوائية X ₁ ، X ₂ ، .. ، X _m ، وسنسميها حزمة صغيرة. إذا كان حجم العينة m كبيرًا بدرجة كافية ، فسيكون متوسط ​​القيمة XC _{X j} قريبًا بدرجة كافية من متوسط ​​جميع ∇Cx ، أي

$$

$$\frac{\sum^m_{j=1} \nabla C_{X_j}}{m} \approx \frac{\sum_x \nabla C_x}{n} = \nabla C \tag{18}$$

حيث يذهب المبلغ الثاني على مجموعة كاملة من بيانات التدريب. بواسطة أجزاء متبادلة ، نحصل عليها

$$

$$\nabla C \approx \frac{1}{m} \sum^m_{j=1} \nabla C_{X_j} \tag{19}$$

مما يؤكد أنه يمكننا تقدير التدرج الكلي من خلال حساب التدرجات اللونية المختارة بشكل عشوائي.

لربط هذا مباشرة بتدريب NS ، دعنا نفترض أن w _k and b _l تدل على أوزان وتهجير NS لدينا. ثم يحدد نزول التدرج العشوائي حزمة مصغرة عشوائية من بيانات الإدخال ، ويتعلم منها

$$

$$w_k \rightarrow w'_k = w_k - \frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \tag{20}$$

$$

$$b_l \rightarrow b'_l = b_l - \frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l} \tag{21}$$

أين هو الجمع على جميع أمثلة التدريب X _j في الحزمة المصغرة الحالية. ثم نختار حزمة صغيرة عشوائية أخرى وندرسها. وهكذا ، حتى نستنفد جميع بيانات التدريب ، والتي تسمى نهاية عصر التدريب. في هذه اللحظة ، بدأنا حقبة جديدة من التعلم.

بالمناسبة ، تجدر الإشارة إلى أن الاتفاقيات المتعلقة بتوسيع نطاق دالة التكلفة وتحديث الأوزان والإزاحة تختلف في حزمة صغيرة. في المعادلة (6) ، قمنا بتحجيم دالة التكلفة 1 / ن مرة. أحيانًا يتجاهل الأشخاص 1 / ن عن طريق إضافة تكاليف أمثلة التدريب الفردية ، بدلاً من حساب المتوسط. هذا مفيد عندما يكون العدد الإجمالي لأمثلة التدريب غير معروف مسبقًا. يمكن أن يحدث هذا ، على سبيل المثال ، عندما تظهر بيانات إضافية في الوقت الحقيقي. بالطريقة نفسها ، تتجاهل قواعد تحديث الحزمة المصغرة (20) و (21) أحيانًا العضو 1 / m أمام المجموع. من الناحية النظرية ، هذا لا يؤثر على أي شيء ، لأنه يعادل التغيير في سرعة التعلم η. ومع ذلك ، يجدر الانتباه إلى عند مقارنة مختلف الأعمال.

يمكن اعتبار نزول التدرج العشوائي بمثابة تصويت سياسي: من الأسهل بكثير أخذ عينة في شكل حزمة مصغرة من تطبيق نزول التدرج على عينة كاملة - تمامًا مثل إجراء استطلاع للرأي في الخروج من موقع ما أسهل من إجراء انتخابات كاملة. على سبيل المثال ، إذا كان حجم مجموعة التدريب لدينا هو n = 60،000 ، مثل MNIST ، وقمنا بعمل عينة من حزمة صغيرة من الحجم m = 10 ، فسنعمل على زيادة تقدير التدرج بمقدار 6000 مرة! بالطبع ، لن يكون التقدير مثاليًا - سيكون هناك تقلب إحصائي فيه - لكنه لا يحتاج إلى أن يكون مثاليًا: نحتاج فقط إلى التحرك في الاتجاه الذي ينقص C ، مما يعني أننا لسنا بحاجة إلى حساب التدرج بدقة. في الممارسة العملية ، يعد النسب التدرج العشوائي أسلوبًا تعليمًا شائعًا وقويًا للجمعية الوطنية ، وقاعدة لمعظم تقنيات التدريس التي سنطورها كجزء من الكتاب.

• - 1. , x w _k → w′ _k = w _k − η ∂C _x / ∂w _k b _l → b′ _l = b _l − η ∂C _x / ∂b _l . . و هكذا. , -, . - ( ). - - 20.

اسمحوا لي أن أنهي هذا القسم بمناقشة موضوع يزعج أحيانًا الأشخاص الذين واجهوا في البداية تدرجًا متدرجًا. في NS ، قيمة C هي دالة للعديد من المتغيرات - جميع الأوزان والإزاحة - وبمعنى ما ، تحدد السطح في مساحة متعددة الأبعاد. يبدأ الناس في التفكير: "سيتعين علي تصور كل هذه الأبعاد الإضافية". ويبدأون في القلق: "لا أستطيع التنقل بأربعة أبعاد ، ناهيك عن خمسة (أو خمسة ملايين)." هل لديهم بعض الجودة الخاصة التي تتمتع بها الرياضيات الفائقة "الحقيقية"؟ بالطبع لا. حتى علماء الرياضيات المحترفون لا يمكنهم تصور الفضاء ذي الأبعاد الأربعة جيدًا - على كل حال. يذهبون إلى الحيل ، وتطوير طرق أخرى لتمثيل ما يحدث. هذا هو بالضبط ما فعلناه:استخدمنا التمثيل الجبري (بدلاً من البصري) لـ toC لفهم كيفية التحرك بحيث تنخفض C. الأشخاص الذين يقومون بعمل جيد مع عدد كبير من الأبعاد لديهم في أذهانهم مكتبة كبيرة من التقنيات المماثلة ؛ خدعتنا جبري مثال واحد فقط. قد لا تكون هذه التقنيات بهذه البساطة التي اعتدنا عليها عند تصور ثلاثة أبعاد ، ولكن عندما تنشئ مكتبة بتقنيات متشابهة ، فإنك تبدأ في التفكير جيدًا في الأبعاد العليا. لن أخوض في التفاصيل ، ولكن إذا كنت مهتمًا ، فقد ترغب في ذلكما الذي اعتدنا عليه عند تصور ثلاثة أبعاد ، ولكن عندما أنشأت مكتبة من التقنيات المتشابهة ، تبدأ في التفكير جيدًا في الأبعاد العليا. لن أخوض في التفاصيل ، ولكن إذا كنت مهتمًا ، فقد ترغب في ذلكما الذي اعتدنا عليه عند تصور ثلاثة أبعاد ، ولكن عندما أنشأت مكتبة من التقنيات المتشابهة ، تبدأ في التفكير جيدًا في الأبعاد العليا. لن أخوض في التفاصيل ، ولكن إذا كنت مهتمًا ، فقد ترغب في ذلكمناقشة لبعض هذه التقنيات من قبل علماء الرياضيات المحترفين الذين اعتادوا على التفكير في أبعاد أعلى. على الرغم من أن بعض التقنيات التي تمت مناقشتها معقدة للغاية ، إلا أن معظم أفضل الإجابات سهلة الاستخدام ومتاحة للجميع.

تطبيق شبكة لتصنيف الأرقام

حسنًا ، دعنا الآن نكتب برنامجًا يتعلم التعرف على الأرقام المكتوبة بخط اليد باستخدام النسب التدرج العشوائي وبيانات التدريب من MNIST. سنفعل هذا مع برنامج قصير في بيثون 2.7 يتكون من 74 خطوط فقط! أول شيء نحتاجه هو تنزيل بيانات MNIST. إذا كنت تستخدم git ، فيمكنك الحصول عليها عن طريق استنساخ مستودع هذا الكتاب:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

إذا لم يكن كذلك ، قم بتنزيل الكود من الرابط .

بالمناسبة ، عندما ذكرت بيانات MNIST في وقت سابق ، قلت إنها مقسمة إلى 60.000 صورة تدريب و 10000 صورة اختبار. هذا هو الوصف الرسمي من MNIST. سنقوم بتحطيم البيانات بشكل مختلف قليلاً. سنترك صور التحقق دون تغيير ، لكننا سنقسم مجموعة التدريب إلى جزأين: 50000 صورة ، والتي سنستخدمها لتدريب الجمعية الوطنية ، و 10000 صورة فردية للتأكيد الإضافي. على الرغم من أننا لن نستخدمها ، إلا أنها ستفيدنا لاحقًا عندما نفهم تكوين بعض المعلمات المفرطة في NS - سرعة التعلم ، وما إلى ذلك - والتي لا تحددها خوارزمية لدينا مباشرةً. على الرغم من أن البيانات المؤكدة ليست جزءًا من مواصفات MNIST الأصلية ، فإن الكثير منها يستخدم MNIST بهذه الطريقة ، وفي مجال HC ، يكون استخدام البيانات المؤيدة شائعًا. الآن ، أتحدث عن "بيانات تدريب MNIST" ، سأقصد بها 50000 كاريتنوك ، وليس الـ 60،000 الأصلي.

بالإضافة إلى بيانات MNIST ، نحتاج أيضًا إلى مكتبة بيثون تسمى Numpy لإجراء عمليات حسابية دقيقة للجبر الخطي. إذا لم يكن لديك ، فيمكنك أخذها من الرابط .

قبل إعطائك البرنامج بالكامل ، اسمحوا لي أن أشرح الميزات الرئيسية لكود NS. يشغل المكان الشبكة فئة الشبكة ، التي نستخدمها لتمثيل الجمعية الوطنية. فيما يلي رمز التهيئة لكائن الشبكة:

 class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] 

تحتوي مجموعة الأحجام على عدد الخلايا العصبية في الطبقات المقابلة. لذلك ، إذا أردنا إنشاء كائن شبكة مع اثنين من الخلايا العصبية في الطبقة الأولى ، وثلاثة الخلايا العصبية في الطبقة الثانية ، وخلية واحدة في الثالثة ، ثم سنكتبها مثل هذا:

 net = Network([2, 3, 1]) 

تتم تهيئة الإزاحات والأوزان في كائن الشبكة بشكل عشوائي باستخدام الدالة npy np.random.randn ، التي تولد توزيعًا غاوسيًا بتوقع رياضي قدره 0 وانحرافًا قياسيًا قدره 1. يعطي هذا التهيئة العشوائية 1. خوارزمية تدرج النسب العشوائي لدينا نقطة بداية. في الفصول التالية ، سنجد أفضل الطرق لتهيئة الأوزان والإزاحة ، لكن هذا يكفي الآن. لاحظ أن رمز تهيئة الشبكة يفترض أن الطبقة الأولى من الخلايا العصبية سيتم إدخالها ، ولا تعيّن لهم تحيزًا ، حيث يتم استخدامها فقط لحساب المخرجات.

لاحظ أيضًا أنه يتم تخزين الإزاحة والأوزان كصفيف من مصفوفات Numpy. على سبيل المثال ، net.weights [1] عبارة عن مصفوفة Numpy تقوم بتخزين الأوزان التي تربط بين الطبقتين الثانية والثالثة من الخلايا العصبية (هذه ليست الطبقة الأولى والثانية ، لأنه في بيثون يأتي ترقيم عناصر المصفوفة من نقطة الصفر). نظرًا لأن كتابة net.weights تستغرق وقتًا طويلاً [1] ، فإننا نشير إلى هذه المصفوفة بأنها w. هذه مصفوفة تجعل وزن _jk هو العلاقة بين الخلايا العصبية kth في الطبقة الثانية والخلية العصبية jth في الطبقة الثالثة. قد يبدو هذا الترتيب للمؤشرات j و k غريبًا - ألا يكون من المنطقي تبديلها؟ لكن الميزة الكبيرة لهذا السجل هي أنه يتم الحصول على ناقل تنشيط الطبقة الثالثة من الخلايا العصبية:

$$

$$a '= \ sigma (wa + b) \ tag {22}$$

دعونا ننظر إلى هذه المعادلة الغنية جدا. a هو ناقل تنشيط الطبقة الثانية من الخلايا العصبية. للحصول على '، نقوم بضرب a بمصفوفة الوزن w ، ونضيف متجه الإزاحة b. ثم نقوم بتطبيق العنصر السيني by حسب العنصر على كل عنصر من عناصر المتجه wa + b (يُطلق عليه اسم ctor vectorization للدالة σ). من السهل التحقق من أن المعادلة (22) تعطي نفس النتيجة مثل القاعدة (4) لحساب الخلايا العصبية السيني.

ممارسة

• اكتب المعادلة (22) في شكل مكون ، وتأكد من أنها تعطي نفس النتيجة مثل القاعدة (4) لحساب الخلايا العصبية السيني.

مع وضع كل ذلك في الاعتبار ، من السهل كتابة التعليمات البرمجية التي تحسب إخراج كائن الشبكة. نبدأ بتحديد السيني:

 def sigmoid(z): return 1.0/(1.0+np.exp(-z)) 

لاحظ أنه عندما تكون المعلمة z عبارة عن متجه Numpy أو صفيف ، فإن Numpy سيقوم تلقائيًا بتطبيق العنصر السيني ، أي في شكل متجه.

إضافة طريقة نشر مباشرة إلى فئة الشبكة ، والتي تأخذ من الشبكة كمدخلات وإرجاع الإخراج المقابل. من المفترض أن المعلمة a هي (n ، 1) ndarray numpy ، وليس المتجه (n ،). هنا n هو عدد الخلايا العصبية المدخلة. إذا حاولت استخدام المتجه (n ،) ، فستحصل على نتائج غريبة.

تطبق الطريقة ببساطة المعادلة (22) على كل طبقة:

  def feedforward(self, a): """       "a"""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a 

بالطبع ، نحن من كائنات الشبكة نحتاج إليهم للتعلم. للقيام بذلك ، سنمنحهم طريقة SGD ، والتي تنفذ النسب التدرج العشوائي. هنا هو رمزه. في بعض الأماكن يكون الأمر غامضًا إلى حد ما ، ولكن أدناه سنحلله بمزيد من التفاصيل.

  def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) 

training_data عبارة عن قائمة من tuples "(x، y)" تمثل مدخلات التدريب والإخراج المطلوب. تعد epochs ومتغيرات mini_batch_size هي عدد epochs التي يجب تعلمها وحجم الحزم المصغرة التي يجب استخدامها. ايتا - سرعة التعلم ، η. إذا تم تعيين test_data ، فسيتم تقييم الشبكة مقابل بيانات التحقق بعد كل عصر ، وسيتم عرض التقدم الحالي. هذا مفيد لتتبع التقدم ، ولكن يبطئ العمل بشكل كبير.

رمز يعمل مثل هذا. في كل عصر ، يبدأ بمزج بيانات التدريب عن طريق الخطأ ، ثم يقسمها إلى حزم صغيرة بالحجم الصحيح. هذه طريقة سهلة لإنشاء نموذج من بيانات التدريب. ثم لكل خطوة صغيرة نطبق خطوة واحدة من نزول التدرج. يتم ذلك عن طريق رمز self.update_mini_batch (mini_batch ، eta) ، الذي يقوم بتحديث أوزان الشبكة وإزاحاتها وفقًا لتكرار واحد من أصل التدرج اللوني باستخدام بيانات التدريب فقط في mini_batch. فيما يلي رمز طريقة update_mini_batch:

  def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] 

يتم معظم العمل عن طريق الخط.

  delta_nabla_b, delta_nabla_w = self.backprop(x, y) 

يستدعي خوارزمية backpropagation - طريقة سريعة لحساب التدرج اللوني لوظيفة التكلفة. لذا ، يقوم update_mini_batch ببساطة بحساب هذه التدرجات لكل مثال تدريبي من mini_batch ، ثم يقوم بتحديث self.weights و self.biases.

حتى الآن ، لن أظهر رمز لـ self.backprop. سنتعلم عن backpropagation في الفصل التالي ، وسيكون هناك رمز self.backprop. في الوقت الحالي ، افترض أنه يتصرف كما هو مذكور ، مع إرجاع تدرج مناسب للتكلفة المرتبطة بمثال التدريب x.

لنلقِ نظرة على البرنامج بالكامل ، بما في ذلك التعليقات التوضيحية. باستثناء وظيفة self.backprop ، يتحدث البرنامج عن نفسه - يتم العمل الرئيسي بواسطة self.SGD و self.update_mini_batch. تستخدم طريقة self.backprop العديد من الوظائف الإضافية لحساب التدرج اللوني ، وهي sigmoid_prime ، التي تحسب مشتق السيني ، و self.cost_derivative ، والتي لن أصفها هنا. يمكنك الحصول على فكرة عنها من خلال النظر في الشفرة والتعليقات. في الفصل التالي سننظر فيها بمزيد من التفصيل. ضع في اعتبارك أنه على الرغم من أن البرنامج يبدو طويلاً ، فإن معظم الكود عبارة عن تعليقات تسهل فهمه. في الحقيقة ، يتكون البرنامج نفسه من 74 سطرًا غير برمجي فقط - وليس فارغًا وليس تعليقات. كل رمز متاح على جيثب .

 """ network.py ~~~~~~~~~~           .      .     ,    .   ,       . """ ####  #   import random #   import numpy as np class Network(object): def __init__(self, sizes): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].               0    1. ,      ,       ,        . """ self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] def feedforward(self, a): """   ,  ``a`` -  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) #   delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """ l      ,      . l = 1    , l = 2 – ,   .    ,   python      .""" for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def evaluate(self, test_data): """    ,      .    –          .""" test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data] return sum(int(x == y) for (x, y) in test_results) def cost_derivative(self, output_activations, y): """    ( C_x /  a)   .""" return (output_activations-y) ####   def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

إلى أي مدى يتعرف البرنامج على الأرقام المكتوبة بخط اليد؟ لنبدأ بتحميل بيانات MNIST. سنفعل ذلك باستخدام برنامج المساعد الصغير mnist_loader.py ، الذي سأصفه أدناه. قم بتشغيل الأوامر التالية في python shell:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

يمكن القيام بذلك ، بالطبع ، في برنامج منفصل ، ولكن إذا كنت تعمل بالتوازي مع كتاب ، فسيكون ذلك أسهل.

بعد تنزيل بيانات MNIST ، قم بإعداد شبكة مكونة من 30 خلية عصبية مخفية. سنفعل ذلك بعد استيراد البرنامج الموضح أعلاه ، والذي يسمى الشبكة:

 >>> import network >>> net = network.Network([784, 30, 10]) 

أخيرًا ، نستخدم نسب التدرج العشوائي للتدريب على بيانات التدريب لمدة 30 عصرًا ، مع حجم رزمة صغيرة تبلغ 10 ، وسرعة تعلم تبلغ η = 3.0:

 >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

إذا كنت تنفذ الشفرة بالتوازي مع قراءة كتاب ، فضع في اعتبارك أن تنفيذ الأمر سيستغرق عدة دقائق. أقترح أن تبدأ كل شيء ، وتستمر في القراءة ، وتحقق بشكل دوري مما ينتجه البرنامج. إذا كنت في عجلة من أمرك ، يمكنك تقليل عدد العصور عن طريق تقليل عدد الخلايا العصبية المخفية ، أو باستخدام جزء فقط من بيانات التدريب. ستعمل شفرة العمل النهائية بشكل أسرع: تم تصميم هذه البرامج النصية بيثون لتجعلك تفهم كيف تعمل الشبكة ، وليست عالية الأداء! وبالطبع ، بعد التدريب ، يمكن أن تعمل الشبكة بسرعة كبيرة على أي منصة حاسوبية تقريبًا. على سبيل المثال ، عندما نعلم الشبكة مجموعة جيدة من الأوزان والإزاحة ، يمكن نقلها بسهولة للعمل على JavaScript في متصفح الويب ، أو كتطبيق أصلي على جهاز محمول. في أي حال ، يتم إجراء نفس الاستنتاج تقريبًا بواسطة البرنامج الذي يدرب الشبكة العصبية. تكتب عدد صور الاختبار المعترف بها بشكل صحيح بعد كل حقبة من التدريب. كما ترون ، حتى بعد حقبة واحدة ، تصل الدقة إلى 9129 من أصل 10000 ، وهذا الرقم مستمر في النمو:

Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000

اتضح أن الشبكة المدربة تعطي نسبة من التصنيف الصحيح حوالي 95 - 95.42 ٪ كحد أقصى! أول محاولة واعدة جدا. أحذرك من أن الكود الخاص بك لن ينتج بالضرورة نفس النتائج بالضبط ، لأننا نهيئة الشبكة بأوزان وإزاحات عشوائية. لهذا الفصل ، اخترت أفضل ثلاث محاولات.

دعنا نعيد تشغيل التجربة عن طريق تغيير عدد الخلايا العصبية المخفية إلى 100. كما كان من قبل ، إذا قمت بتشغيل الكود في نفس الوقت الذي تقرأ فيه ، ضع في اعتبارك أن الأمر يستغرق الكثير من الوقت (على جهازي ، كل عصر يستغرق عدة عشرات من الثواني) ، لذلك من الأفضل أن تقرأ بالتوازي مع تنفيذ التعليمات البرمجية.

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

بطبيعة الحال ، هذا يحسن النتيجة إلى 96.59 ٪. في هذه الحالة على الأقل ، يساعد استخدام مزيد من الخلايا العصبية المخفية في الحصول على نتائج أفضل.

تشير تعليقات القراء إلى أن نتائج هذه التجربة تختلف اختلافًا كبيرًا وأن بعض نتائج التعلم أسوأ بكثير. باستخدام التقنيات من الفصل 3 للحد بشكل كبير من تنوع كفاءة العمل من تشغيل واحد إلى آخر.

بالطبع ، من أجل تحقيق هذه الدقة ، كان علي اختيار عدد معين من العصور للتعلم ، وحجم الحزمة المصغرة وسرعة التعلم η. كما ذكرت أعلاه ، يطلق عليها "معلمات فرعيّة من جمعيتنا الوطنية - لتمييزها عن المعلمات البسيطة (الأوزان والإزاحة) التي تقوم الخوارزمية بضبطها أثناء التدريب. إذا اخترنا hyperparameters بشكل سيئ ، فسنحصل على نتائج سيئة. لنفترض ، على سبيل المثال ، أننا اخترنا معدل التعلم η = 0.001:

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data) 

النتائج أقل إثارة للإعجاب:

Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000

ومع ذلك ، يمكنك أن ترى أن كفاءة الشبكة تنمو ببطء مع مرور الوقت. يشير هذا إلى أنه يمكنك محاولة زيادة سرعة التعلم ، على سبيل المثال ، إلى 0.01. في هذه الحالة ، ستكون النتائج أفضل ، مما يشير إلى الحاجة إلى زيادة السرعة (إذا كان التغيير يحسّن الموقف ، فتغير أكثر!). إذا قمت بذلك عدة مرات ، فسنصل في النهاية إلى 1.0 = 1.0 (وأحيانًا حتى 3.0) ، وهو قريب من تجاربنا السابقة. لذلك ، على الرغم من أننا قمنا في البداية باختيار المقاييس الفرعية بشكل سيئ ، فقد جمعنا على الأقل معلومات كافية لتكون قادرًا على تحسين اختيارنا للمعلمات.

بشكل عام ، تصحيح NA أمر معقد. وينطبق هذا بشكل خاص عندما ينتج عن اختيار المعلمات التشعبية الأولية نتائج لا تتجاوز الضوضاء العشوائية. لنفترض أننا نحاول استخدام بنية ناجحة من 30 خلية عصبية ، لكن مع تغيير سرعة التعلم إلى 100.0:

 >>> net = network.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data) 

في النهاية ، اتضح أننا ذهبنا بعيداً وأخذنا الكثير من السرعة:

Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000

الآن تخيل أننا نقترب من هذه المهمة لأول مرة. بالطبع ، نعلم من التجارب المبكرة أنه سيكون من الصواب تقليل سرعة التعلم. ولكن إذا كنا نقترب من هذه المهمة لأول مرة ، فلن يكون لدينا ناتج يمكن أن يقودنا إلى الحل الصحيح. هل يمكن أن نبدأ في التفكير في أننا ربما اخترنا المعلمات الأولية الخاطئة للأوزان والإزاحة ، ومن الصعب أن تتعلم الشبكة؟ أو ربما ليس لدينا بيانات تدريب كافية للحصول على نتيجة ذات معنى؟ ربما لم ننتظر عصور كافية؟ ربما شبكة عصبية مع مثل هذه الهندسة المعمارية ببساطة لا يمكن أن تتعلم كيفية التعرف على الأرقام المكتوبة بخط اليد؟ ربما تكون سرعة التعلم بطيئة للغاية؟ عندما تقترب من المهمة لأول مرة ، لن تكون لديك ثقة أبدًا.

من هذا ، يجدر تعلم الدرس القائل إن تصحيح أخطاء NS ليس مهمة تافهة ، وهذا ، مثل البرمجة العادية ، جزء من الفن. يجب أن تتعلم فن تصحيح الأخطاء هذا للحصول على نتائج جيدة من NS. بشكل عام ، نحن بحاجة إلى تطوير منهجي لتحديد المقاييس الفائقة الجيدة والعمارة الجيدة. سنناقش هذا بالتفصيل في الكتاب ، بما في ذلك كيفية اختيار المعلمات أعلاه.

ممارسة

• حاول إنشاء شبكة مكونة من طبقتين فقط - الإدخال والإخراج ، دون إخفاء - مع 784 و 10 خلايا عصبية ، على التوالي. تدريب الشبكة مع النسب الانحدار العشوائي. ما دقة التصنيف التي تحصل عليها؟

سبق لي أن تخطيت تفاصيل تحميل بيانات MNIST. يحدث ذلك بكل بساطة. هنا هو رمز لإكمال الصورة. يتم وصف هياكل البيانات في التعليقات - كل شيء بسيط ، tuples ومصفوفات من الكائنات ndarray Numpy (إذا لم تكن معتادًا على مثل هذه الكائنات ، تخيلها كمتجهات).

 """ mnist_loader ~~~~~~~~~~~~      MNIST.       ``load_data``  ``load_data_wrapper``.  , ``load_data_wrapper`` -  ,     . """ ####  #  import cPickle import gzip #  import numpy as np def load_data(): """  MNIST   ,  ,    . ``training_data``      .    .  numpy ndarray  50 000 .   –     numpy ndarray  784 ,  28 * 28 = 784    MNIST.  –  numpy ndarray  50 000 .   –   0  9   ,    . ``validation_data``  ``test_data`` ,    10 000 .    ,           ``training_data``.    - ``load_data_wrapper()``. """ f = gzip.open('../data/mnist.pkl.gz', 'rb') training_data, validation_data, test_data = cPickle.load(f) f.close() return (training_data, validation_data, test_data) def load_data_wrapper(): """ ,  ``(training_data, validation_data, test_data)``.   ``load_data``,         .  , ``training_data`` -    50 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   . ``y`` -  10- numpy.ndarray,   ,     ``x``. ``validation_data``  ``test_data`` -  ,   10 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   ,  ``y`` -   ,  ,   ( ),  ``x``. ,  ,           .         .""" tr_d, va_d, te_d = load_data() training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] training_results = [vectorized_result(y) for y in tr_d[1]] training_data = zip(training_inputs, training_results) validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]] validation_data = zip(validation_inputs, va_d[1]) test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]] test_data = zip(test_inputs, te_d[1]) return (training_data, validation_data, test_data) def vectorized_result(j): """ 10-    1.0   j     .      (0..9)     .""" e = np.zeros((10, 1)) e[j] = 1.0 return e 

قلت إن برنامجنا يحقق نتائج جيدة. ماذا يعني هذا؟ جيد مقارنة بماذا؟ من المفيد الحصول على نتائج بعض الاختبارات الأساسية البسيطة التي يمكنك من خلالها إجراء مقارنة لفهم معنى "النتائج الجيدة". أبسط مستوى أساسي ، بالطبع ، سيكون تخمينًا عشوائيًا. ويمكن القيام بذلك في حوالي 10 ٪ من الحالات. ونظهر نتيجة أفضل بكثير!

ماذا عن مستوى قاعدة أقل تافهة؟ دعونا ننظر في كيف الظلام الصورة. على سبيل المثال ، عادة ما تكون الصورة 2 أغمق من الصورة 1 ، ببساطة لأنها تحتوي على مزيد من وحدات البكسل الداكنة ، كما هو موضح في الأمثلة أدناه:



يتبع ذلك أنه يمكننا حساب متوسط ​​الظلام لكل رقم من 0 إلى 9. عندما نحصل على صورة جديدة ، نحسب ظلامها ، ونخمن أنها تُظهر شخصية ذات أقرب ظلام متوسط. هذا إجراء بسيط سهل البرمجة ، لذا لن أكتب رمزًا - إذا كان الأمر مهتمًا ، فهو يقع على GitHub . لكن هذا يعد تحسينًا كبيرًا مقارنةً بالتخمينات العشوائية - حيث يتعرف الرمز بشكل صحيح على 2225 من أصل 10000 صورة ، أي يعطي دقة 22.25٪.

ليس من الصعب العثور على أفكار أخرى تحقق الدقة في حدود 20 إلى 50٪. بعد العمل أكثر من ذلك بقليل ، يمكنك أن تتجاوز 50 ٪. ولكن لتحقيق دقة أكبر بكثير ، من الأفضل استخدام خوارزميات MO الموثوقة. لنجرب أحد أشهر الخوارزميات ، طريقة متجه الدعم أو SVM. إذا لم تكن معتادًا على SVM ، فلا تقلق ، لسنا بحاجة إلى فهم هذه التفاصيل. نحن فقط نستخدم مكتبة بيثون تسمى scikit-learn ، والتي توفر واجهة بسيطة للمكتبة السريعة C لـ SVM ، المعروفة باسم LIBSVM .

إذا قمنا بتشغيل scikit-مصنف SVM في الإعدادات الافتراضية ، فسنحصل على التصنيف الصحيح البالغ 9،435 من أصل 10،000 ( يتوفر الكود على الرابط). هذا بالفعل تحسن كبير على النهج الساذج لتصنيف الصور حسب الظلام. هذا يعني أن SVM يعمل بشكل جيد مثل NS لدينا ، فقط أسوأ قليلاً. في الفصول التالية ، سنتعرف على التقنيات الجديدة التي ستتيح لنا تحسين NS لدينا بحيث تتفوق بشكل كبير على SVM.

لكن هذا ليس كل شيء.النتيجة 9 435 من أصل 10000 من scikit-Learn يتم تحديد الإعدادات الافتراضية. يحتوي SVM على العديد من المعلمات التي يمكن ضبطها ، ويمكنك البحث عن المعلمات التي تحسن هذه النتيجة. لن أخوض في التفاصيل ؛ يمكن قراءتها في المقال بواسطة أندرياس مولر. وأوضح أنه من خلال القيام بالعمل لتحسين المعلمات ، من الممكن تحقيق دقة لا تقل عن 98.5 ٪. بمعنى آخر ، فإن SVM مضبوط جيدًا يجعل رقمًا واحدًا من أصل 70. نتيجة جيدة! يمكن تحقيق أكثر؟

اتضح ما في وسعهم. اليوم ، يتفوق NS موالفة جيدًا على أي تقنية أخرى معروفة في حل MNIST ، بما في ذلك SVM. سجل لعام 2013تصنف بشكل صحيح 9،979 من أصل 10000 صورة. وسوف نرى معظم التقنيات المستخدمة لهذا في هذا الكتاب. هذا المستوى من الدقة قريب من الإنسان ، وربما يتجاوزه ، حيث يصعب فك تشفير عدة صور من MNIST حتى بالنسبة للبشر ، على سبيل المثال: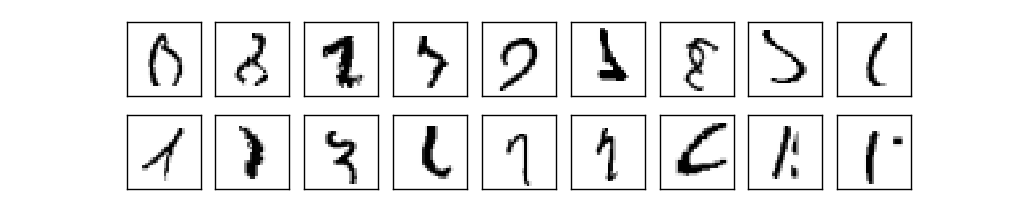



أعتقد أنك ستوافق على أنه يصعب تصنيفها! مع وجود مثل هذه الصور في مجموعة بيانات MNIST ، من المدهش أن NS يمكن أن يتعرف بشكل صحيح على جميع الصور من 10000 ، باستثناء 21. عادةً ، يعتبر المبرمجون أن الخوارزمية المعقدة مطلوبة لحل هذه المهمة المعقدة. ولكن حتى NS في العمليستخدم حامل السجل خوارزميات بسيطة إلى حد ما ، وهي اختلافات صغيرة عن تلك التي درسناها في هذا الفصل. يظهر كل التعقيد تلقائيًا أثناء التدريب بناءً على بيانات التدريب. بمعنى ما ، فإن معنويات نتائجنا والنتائج الواردة في أعمال أكثر تعقيدًا هي أن ذلك بالنسبة لبعض المهام

خوارزمية معقدة al خوارزمية تدريب بسيطة + بيانات تدريب جيدة

للتعلم العميق

على الرغم من أن شبكتنا تظهر أداءً رائعًا ، إلا أنها تتحقق بطريقة غامضة. يتم اكتشاف الأوزان وشبكات الخلط تلقائيًا. لذلك ، ليس لدينا تفسير جاهز لكيفية قيام الشبكة بما تفعله. هل هناك أي طريقة لفهم المبادئ الأساسية للتصنيف من خلال شبكة من الأرقام المكتوبة بخط اليد؟ وهل من الممكن ، بالنظر إليهم ، تحسين النتيجة؟

نعيد صياغة هذه الأسئلة بشكل أكثر صرامة: لنفترض أنه خلال بضعة عقود سوف تتحول NS إلى ذكاء اصطناعي (AI). هل نفهم كيف تعمل هذه الذكاء الاصطناعي؟ ربما ستبقى الشبكات غير مفهومة لنا ، بأوزانها وإزاحاتها ، حيث يتم تخصيصها تلقائيًا. في السنوات الأولى من أبحاث الذكاء الاصطناعى ، كان الناس يأملون في أن محاولة تكوين الذكاء الاصطناعي ستساعدنا أيضًا على فهم المبادئ التي يقوم عليها الذكاء ، وربما عمل الدماغ البشري. ومع ذلك ، في النهاية قد يتضح أننا لن نفهم الدماغ أو كيف تعمل الذكاء الاصطناعى!

للتعامل مع هذه القضايا ، دعونا نتذكر تفسير الخلايا العصبية الاصطناعية التي قدمتها في بداية الفصل - أن هذه طريقة لوزن الأدلة. لنفترض أننا نريد تحديد ما إذا كان وجه شخص ما على صورة:







يمكن التعامل مع هذه المشكلة بنفس طريقة التعرف على خط اليد: باستخدام بكسلات الصور كمدخلات في NS ، وسيكون إخراج NS أحد الخلايا العصبية التي ستقول ، "نعم ، هذا وجه" ، أو "لا ، هذا ليس وجهًا ".

لنفترض أننا نفعل ذلك ، ولكن دون استخدام خوارزمية التعلم. سنحاول إنشاء شبكة يدويًا ، واختيار الأوزان والإزاحة المناسبة. كيف يمكننا التعامل مع هذا؟ للحظة ، ننسى الجمعية الوطنية ، يمكننا تقسيم المهمة إلى مهام فرعية: هل توجد صورة للعيون في الزاوية اليسرى العليا؟ هل هناك عين في الزاوية اليمنى العليا؟ هل هناك أنف وسطى؟ هل هناك فم أسفل الوسط؟ هل يوجد شعر في الأعلى؟ و هكذا.

إذا كانت الإجابات على العديد من هذه الأسئلة إيجابية ، أو حتى "ربما نعم" ، فإننا نستنتج أن الصورة قد يكون لها وجه. على العكس ، إذا كانت الإجابات "لا" ، فمن المحتمل ألا يكون هناك شخص.

هذا ، بطبيعة الحال ، هو مجريات الأمور التقريبية ، ولها العديد من أوجه القصور. ربما هذا رجل أصلع ، وليس لديه شعر. ربما يمكننا رؤية جزء فقط من الوجه ، أو الوجه بزاوية ، بحيث يتم إغلاق بعض أجزاء الوجه. ومع ذلك ، فإن إرشادي يشير إلى أنه إذا استطعنا حل المشكلات الفرعية بمساعدة الشبكات العصبية ، فربما يمكننا إنشاء NSs للتعرف على الوجوه من خلال الجمع بين شبكات المهام الفرعية. فيما يلي بنية محتملة لهذه الشبكة حيث تتم الإشارة إلى الشبكات الفرعية بواسطة المستطيلات. هذه ليست طريقة واقعية تمامًا لحل مشكلة التعرف على الوجوه: إنها ضرورية لمساعدتنا على فهم عمل الشبكات العصبية بشكل حدسي.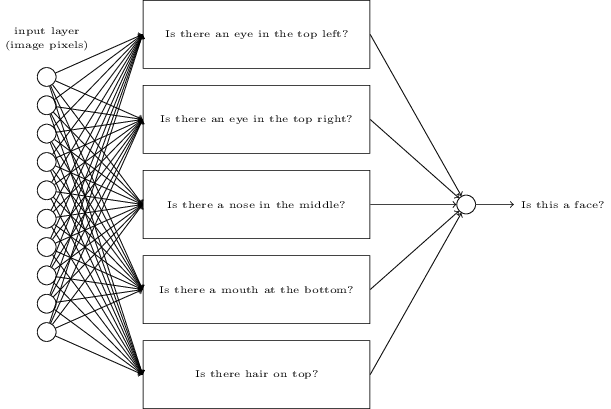


توجد في المستطيلات مهام فرعية: هل توجد صورة للعينين في الزاوية اليسرى العليا؟ هل هناك عين في الزاوية اليمنى العليا؟ هل هناك أنف وسطى؟ هل هناك فم أسفل الوسط؟ هل يوجد شعر في الأعلى؟ و هكذا.

من الممكن أيضًا تفكيك الشبكات الفرعية إلى مكونات. خذ مسألة وجود عين في الزاوية اليسرى العليا. يمكن تمييزه في أسئلة مثل: "هل هناك حاجب؟" ، "هل هناك رموش؟" ، "هل هناك تلميذ؟" و هكذا. بالطبع ، يجب أن تحتوي الأسئلة على معلومات حول الموقع - "هل يقع الحاجب في أعلى اليسار ، فوق التلميذ؟" ، وما إلى ذلك - لكن لنبسطه الآن. لذلك ، يمكن تفكيك الشبكة التي تجيب على سؤال حول وجود العين في المكونات:


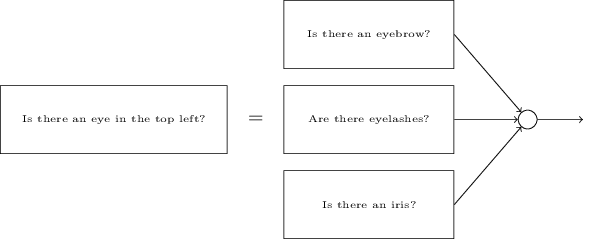"هل هناك حاجب؟" ، "هل هناك رموش؟" ، "هل هناك تلميذ؟"

يمكن تقسيم هذه الأسئلة إلى أسئلة صغيرة ، في خطوات عبر طبقات عديدة. نتيجة لذلك ، سنعمل مع شبكات فرعية تجيب على مثل هذه الأسئلة البسيطة التي يمكن تفكيكها بسهولة على مستوى البكسل. قد تتعلق هذه الأسئلة ، على سبيل المثال ، بوجود أو عدم وجود أشكال بسيطة في أماكن معينة من الصورة. سوف الخلايا العصبية الفردية المرتبطة بكسل تكون قادرة على الاستجابة لهم.

والنتيجة هي شبكة تقسم الأسئلة المعقدة للغاية - سواء كان الشخص موجودًا في الصورة - إلى أسئلة بسيطة للغاية يمكن الإجابة عليها على مستوى البكسل الفردي. ستقوم بذلك من خلال سلسلة من العديد من الطبقات ، حيث تجيب الطبقات الأولى عن أسئلة بسيطة ومحددة للغاية حول الصورة ، وتقوم الأخيرة بإنشاء تسلسل هرمي للمفاهيم الأكثر تعقيدًا وتجريدًا. تسمى الشبكات ذات البنية متعددة الطبقات - طبقتان أو أكثر من الطبقات المخفية - الشبكات العصبية العميقة (GNS).

بالطبع ، لم أتحدث عن كيفية عمل هذه الشبكة الفرعية العودية. بالتأكيد سيكون من غير العملي تحديد الأوزان والإزاحة يدويًا. نود استخدام خوارزميات التدريب حتى تتعلم الشبكة تلقائيًا الأوزان والإزاحة - ومن خلالها التسلسل الهرمي للمفاهيم - بناءً على بيانات التدريب. حاول الباحثون في الثمانينيات والتسعينيات استخدام النسب التدرج الانحداري والتكاثر الخلفي لتدريب GNS. لسوء الحظ ، باستثناء بعض الهياكل الخاصة ، لم تنجح. تم تدريب الشبكات ، ولكن ببطء شديد ، وفي الممارسة العملية كانت بطيئة للغاية لاستخدامها بطريقة أو بأخرى.

منذ عام 2006 ، تم تطوير العديد من التقنيات لتدريب STS. وهي تستند إلى نزول التدرج العشوائي وانتشار الظهر ، ولكنها تحتوي أيضًا على أفكار جديدة. سمحوا لتدريب شبكات أعمق بكثير - اليوم الناس بهدوء تدريب الشبكات مع 5-10 طبقات. وتبين أنها تحل العديد من المشكلات أفضل بكثير من NS NS الضحلة ، أي الشبكات ذات الطبقة المخفية. السبب ، بالطبع ، هو أن STS يمكنها إنشاء تسلسل هرمي معقد من المفاهيم. هذا مشابه لكيفية استخدام لغات البرمجة لمخططات نمطية وأفكار تجريدية بحيث يمكنهم إنشاء برامج كمبيوتر معقدة. إن المقارنة بين NS عميقًا و NS ضحل تقريبًا هي كيفية مقارنة لغة برمجة يمكنها إجراء مكالمات دالة مع لغة لا. لا يبدو التجريد في NS في لغات البرمجة ،ولكن لديه نفس الأهمية.