ما هو الاحتمال وكيفية حسابه

فليكن هناك بعض التجارب المجردة التي قد تحدث فيها حدث معين. تم إجراء هذه التجربة خمس مرات ، وفي أربعة منها حدث نفس الحدث. ما هي الاستنتاجات التي يمكن استخلاصها من هذه 4/5؟



هناك صيغة برنولي تعطي الجواب مع ما يحدث 4 من 5 مع احتمال أولي معروف. لكنها لم تقدم إجابة ، ما كان الاحتمال الأولي إذا كانت الأحداث 4 من أصل 5. دعنا نترك جانبا صيغة برنولي.

سننشئ برنامجًا بسيطًا صغيرًا يحاكي عمليات الاحتمال لمثل هذه الحالة ، استنادًا إلى نتيجة الحسابات التي نبني فيها رسمًا بيانيًا.

void test1() { uint sz_ar_events = 50; //    uint ar_events[sz_ar_events]; //        for (uint i = 0; i < sz_ar_events; ++i) ar_events[i] = 0; uint cnt_events = 0; //       uint k = 4; // k   n  uint n = 5; //   while (cnt_events < 1000000) { //     // ,   0..1 double probability = get_random_real_0_1(); uint c_true = 0; for (uint i = 0; i < n; ++i) { //     probability, //  n-         bool v = get_true_with_probability(probability); if (v) ++c_true; } //   n-  k- ,      if (c_true == k) { uint idx = lrint(floor(probability*sz_ar_events)); assert( idx < sz_ar_events ); // ,      ++cnt_events; //   ++ar_events[idx]; //      } } //   for (uint i = 0; i < sz_ar_events; ++i) { double p0 = DD(i)/sz_ar_events; //  : //        double v = DD(ar_events[i])/cnt_events / (1.0/sz_ar_events); printf("%4.2f %f\n", p0, v); } } 

يمكن العثور على رمز هذا البرنامج هنا ، جنبًا إلى جنب مع الوظائف الإضافية.

تم طرح الحساب في Excel وجعل جدولًا زمنيًا.

يمكن تسمية هذا الإصدار من الرسم البياني بتوزيع كثافة الاحتمال لقيمة الاحتمال. مساحتها مساوية للوحدة الموزعة في هذا التل.

لإكمال الصورة ، سوف أذكر أن هذا الرسم البياني يتوافق مع الرسم البياني وفقًا لمعادلة Bernoulli لمعلمة الاحتمال وضربه N + 1 في عدد التجارب.

كذلك في النص ، حيث أستخدم جزءًا صغيرًا من النموذج k / n في المقالة ، فهذا ليس تقسيمًا ، فهذه أحداث k من تجارب n ، حتى لا أكتب k من n في كل مرة.

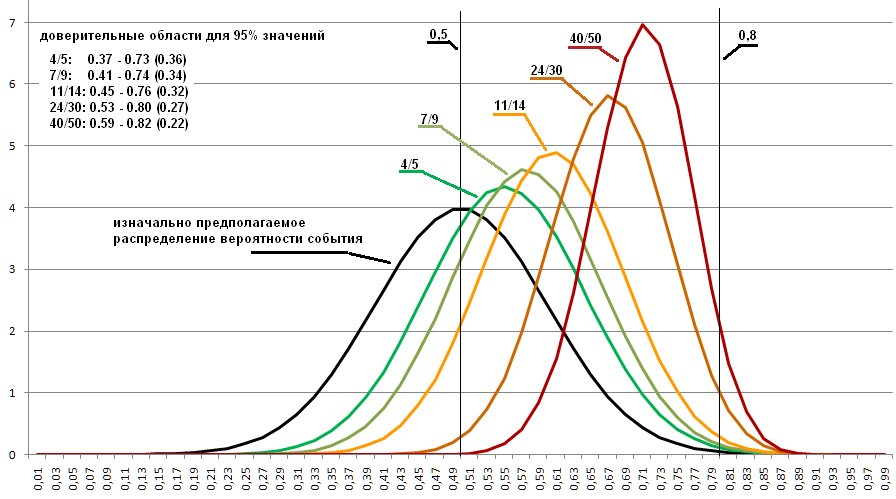
التالي. من الممكن زيادة عدد التجارب ، وللحصول على منطقة أضيق من موقع القيم الرئيسية لقيمة الاحتمال ، ولكن بغض النظر عن كيفية زيادتها ، لن يتم تقليل هذه المنطقة إلى منطقة الصفر ذات الاحتمال المعروف.

يوضح الرسم البياني أدناه توزيعات 4/5 و 7/9 و 11/14 و 24/30. كلما كانت المنطقة أضيق ، كلما كان التلة أعلى ، تكون المنطقة عبارة عن وحدة ثابتة. لقد تم اختيار هذه العلاقات لأنها تدور حول 0.8 ، وليس لأنها بالضبط تلك التي يمكن أن تنشأ عند 0.8 من الاحتمال الأولي. تم تحديده لإظهار نطاق القيم الممكنة الذي يبقى حتى مع إجراء 30 تجربة.

رمز البرنامج لهذا الرسم البياني هنا .


يستنتج من ذلك أنه في الواقع لا يمكن تحديد الاحتمالية التجريبية بدقة ، لكن لا يمكننا إلا أن نفترض منطقة الموقع المحتمل لمثل هذه الكمية ، بدقة تعتمد على عدد القياسات التي تم أخذها.

بغض النظر عن عدد التجارب التي يتم إجراؤها ، هناك دائمًا احتمال أن يكون الاحتمال المبدئي هو 0.0001 و 0.9999. للبساطة ، يتم تجاهل القيم غير المرجح المتطرفة. ونأخذ ، على سبيل المثال ، 95٪ من المساحة الرئيسية لجدول التوزيع.

يسمى هذا الشيء فترات الثقة. لم أحقق أي توصيات بشأن مقدار ولماذا يجب ترك الاهتمام. للتنبؤ بالطقس ، خذ أقل ، لإطلاق المزيد من المكوكات الفضائية. كما أنهم عادةً لا يذكرون فاصل الثقة الذي يتم استخدامه مع ذلك لاحتمال الأحداث وما إذا كان يتم استخدامه على الإطلاق.

في برنامجي ، يتم حساب حدود الفاصل الزمني للثقة هنا .

لقد اتضح أن احتمال الحدث يتم تحديده من خلال كثافة الاحتمال لقيمة الاحتمال ، وأنه لا يزال من الضروري فرض نسبة مئوية من مساحة القيم الرئيسية عليه حتى تتمكن على الأقل من تحديد نوع الاحتمال المحتمل للحدث قيد الدراسة.

الآن ، عن تجربة أكثر واقعية.

دع الجميع يشعرون بالملل من العملة المعدنية ، وألقوا هذه العملة المعدنية واحصلوا على 4 قطرات من أصل 5 - وهي حالة حقيقية للغاية. في الواقع ، هذا ليس هو نفسه كما هو موضح أعلى قليلاً. كيف يختلف هذا عن التجربة السابقة؟

تم وصف التجربة السابقة على افتراض أن احتمال وقوع الحدث يمكن توزيعه بالتساوي على الفاصل الزمني من 0 إلى 1. في البرنامج ، يتم تحديد هذا بواسطة السطر " احتمال مزدوج" = get_random_real_0_1 ()؛ . ولكن لا توجد عملات معدنية مع احتمال السقوط ، مثلا ، 0.1 أو 0.9 دائما على جانب واحد.

إذا أخذت ألف قطعة نقدية مختلفة من عادية إلى أكثر منحنية ، ولكل منها إجراء قياس للخسارة من خلال رميها بألف مرة أو أكثر ، فسوف تظهر أنها تسقط فعليًا على جانب واحد في النطاق من 0.4 إلى 0.6 (هذه أرقام عشوائية ، لن أفعل لكنني أسعى إلى الحصول على 1000 قطعة نقدية وإرم كل 1000 مرة).

كيف تغير هذه الحقيقة برنامج محاكاة احتمالات عملة واحدة معينة ، والتي تم استلام 4 من أصلها الخمسة؟

لنفترض أن توزيع الخسارة على جانب واحد للعملات المعدنية يوصف بأنه تقريب للرسم البياني للتوزيع الطبيعي المأخوذ بمعلمات متوسط ​​= 0.5 ، الانحراف المعياري = 0.1. (في الرسم البياني أدناه يظهر باللون الأسود).

عندما أقوم بتغيير أحد البرامج في أحد البرامج من توزيع متساوٍ إلى موزعة وفقًا للقاعدة المحددة ، أحصل على الرسوم البيانية التالية:


رمز هذا الخيار هنا .

يمكن أن نرى أن التوزيعات قد تحولت بقوة والآن تحدد منطقة مختلفة قليلاً يكون فيها الاحتمال المرغوب فيه محتملاً للغاية. لذلك ، إذا كان من المعروف ما هي الاحتمالات الموجودة لتلك الأشياء ، والتي نريد قياس أحدها ، فإن هذا يمكن أن يحسن النتيجة إلى حد ما.

نتيجة لذلك ، لا يعني 4/5 أي شيء ، وحتى 50 من التجارب التي أجريت ليست مفيدة للغاية. هذه معلومات قليلة جدًا لتحديد نوع الاحتمال الذي لا يزال أساس التجربة.

== تحديث ==

كما ذكر jzha في التعليقات ، وهو شخص يعرف الرياضيات بشكل كبير ، يمكن أيضًا إنشاء هذه الرسوم البيانية باستخدام صيغ دقيقة. ولكن الغرض من هذه المقالة لا يزال هو توضيح قدر الإمكان كيف يتم تشكيل الاحتمال الذي يدعو إليه الجميع في الحياة اليومية.

من أجل بنائها باستخدام صيغ دقيقة ، من الضروري النظر في البيانات المتاحة حول توزيع الاحتمالات لجميع العملات من خلال تقريب توزيع بيتا ، ومن خلال حساب التوزيعات ، استخلاص الحسابات. مثل هذا المخطط هو قدر كبير من التفسيرات حول كيفية القيام بذلك ، وإذا وصفته هنا ، فسوف يتحول إلى مقال حول الحسابات الرياضية ، وليس الاحتمالات اليومية.

كيفية الحصول على الصيغ وصفت حالة خاصة مع عملة معدنية ، راجع التعليقات من jzha .