عند تشغيل الاستعلامات في
ClickHouse ، قد تلاحظ أن المُنشئ يُظهر غالبًا دالة
LZ_decompress_fast بالقرب من الجزء العلوي. ما الذي يحدث؟ هذا السؤال جعلنا نتساءل عن كيفية اختيار أفضل خوارزمية ضغط.
تقوم ClickHouse بتخزين البيانات في نموذج مضغوط. عند تشغيل الاستعلامات ، يحاول ClickHouse القيام بأقل قدر ممكن ، من أجل الحفاظ على موارد وحدة المعالجة المركزية. في كثير من الحالات ، يتم بالفعل تحسين جميع الحسابات التي يحتمل أن تستغرق وقتًا كبيرًا ، بالإضافة إلى أن المستخدم كتب استعلامًا مدروسًا جيدًا. ثم كل ما تبقى هو القيام بأداء الضغط.
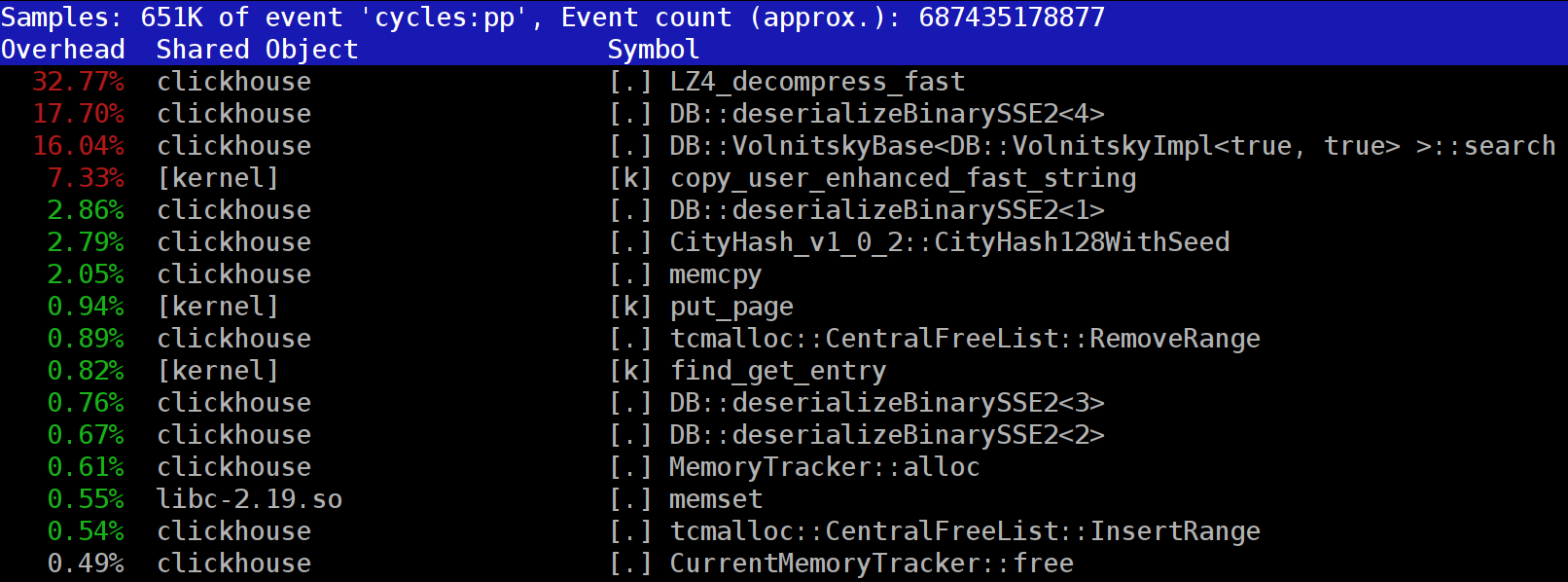
فلماذا يصبح الضغط LZ4 عنق الزجاجة؟ يبدو LZ4 مثل
خوارزمية خفيفة للغاية : عادةً ما يكون معدل إلغاء ضغط البيانات من 1 إلى 3 جيجابايت / ثانية لكل كور معالج ، اعتمادًا على البيانات. هذا أسرع بكثير من النظام الفرعي للقرص النموذجي. علاوة على ذلك ، نحن نستخدم جميع النوى المتوفرة لوحدة المعالجة المركزية (CPU) ، كما يتم قياس الضغط بشكل خطي عبر جميع النوى المادية.
ومع ذلك ، هناك نقطتان يجب مراعاتهما. أولاً ، يتم قراءة البيانات المضغوطة من القرص ، ولكن يتم إعطاء سرعة إلغاء الضغط من حيث مقدار البيانات غير المضغوطة. إذا كانت نسبة الضغط كبيرة بدرجة كافية ، فلا يوجد شيء تقريبًا للقراءة من الأقراص. ولكن سيكون هناك الكثير من البيانات التي تم إلغاء ضغطها ، وهذا يؤثر بشكل طبيعي على استخدام وحدة المعالجة المركزية: في حالة LZ4 ، يكون مقدار العمل الضروري لإلغاء ضغط البيانات متناسباً تقريبًا مع حجم البيانات التي تم إلغاء ضغطها بنفسها.
ثانياً ، إذا تم تخزين البيانات مؤقتًا ، فقد لا تحتاج إلى قراءة البيانات من الأقراص على الإطلاق. يمكنك الاعتماد على ذاكرة التخزين المؤقت للصفحة أو استخدام ذاكرة التخزين المؤقت الخاصة بك. التخزين المؤقت أكثر فعالية في قواعد البيانات الموجهة للأعمدة ، حيث تبقى الأعمدة المستخدمة بشكل متكرر في ذاكرة التخزين المؤقت. هذا هو السبب في أن LZ4 غالبًا ما يبدو أنه عنق الزجاجة من حيث تحميل وحدة المعالجة المركزية.
هذا يطرح سؤالين آخرين. أولاً ، إذا كان تخفيف الضغط يبطئنا ، فهل يستحق ضغط البيانات لتبدأ؟ لكن هذه التكهنات لا علاقة لها بالممارسة. حتى وقت قريب ، لم يقدم تكوين ClickHouse سوى خيارين لضغط البيانات - LZ4 و
Zstandard . يتم استخدام LZ4 بشكل افتراضي. التحول إلى Zstandard يجعل الضغط أقوى وأبطأ. ولكن لم يكن هناك خيار لتعطيل الضغط تمامًا ، حيث يُفترض أن LZ4 يوفر الحد الأدنى المعقول من الضغط الذي يمكن استخدامه دائمًا. (وهذا هو بالضبط السبب في أنني أحب LZ4.)
ولكن بعد ذلك ظهر شخص غريب غامض في
دردشة دعم ClickHouse الدولية ، وقال إن لديه نظامًا فرعيًا سريعًا للقرص (مع NVMe SSD) وأن الضغط هو الشيء الوحيد الذي يبطئ من استفساراته ، لذلك سيكون من الجيد أن تكون قادرًا على تخزين البيانات دون ضغط. أجبت أنه ليس لدينا هذا الخيار ، لكن سيكون من السهل إضافته. بعد بضعة أيام ، تلقينا
طلب سحب تطبيق طريقة الضغط
none . لقد طلبت من المساهم تقديم تقرير حول مقدار هذا الخيار الذي ساعد في تسريع الاستعلامات. كان الرد أن هذه الميزة الجديدة قد تحولت إلى فائدة من الناحية العملية ، حيث بدأت البيانات غير المضغوطة تشغل مساحة كبيرة على القرص ولم تتناسب مع محركات أقراص NVMe هذه.
السؤال الثاني الذي يطرح نفسه هو أنه في حالة وجود ذاكرة تخزين مؤقت ، فلماذا لا تستخدمه لتخزين البيانات التي تم فك ضغطها بالفعل؟ هذا هو احتمال قابل للتطبيق من شأنه أن يلغي الحاجة إلى تخفيف الضغط في كثير من الحالات. يحتوي ClickHouse أيضًا على ذاكرة تخزين مؤقت مثل هذا:
ذاكرة التخزين المؤقت للكتل التي تم فك ضغطها . ولكن من المؤسف أن نضيع الكثير من ذاكرة الوصول العشوائي على هذا. لذلك عادة ما يكون من المنطقي فقط استخدام طلبات البحث الصغيرة والمتسلسلة التي تستخدم بيانات متطابقة تقريبًا.
استنتاجنا هو أنه من الأفضل دائمًا تخزين البيانات بتنسيق مضغوط. دائما كتابة البيانات إلى القرص في شكل مضغوط. نقل البيانات عبر الشبكة مع الضغط ، كذلك. في رأيي ، فإن الضغط الافتراضي له ما يبرره حتى عند نقل البيانات داخل مركز بيانات واحد في شبكة بحجم 10 جيجابايت دون زيادة الاشتراك ، في حين أن نقل البيانات غير المضغوطة بين مراكز البيانات أمر غير مقبول.
لماذا LZ4؟
لماذا تختار LZ4؟ لا يمكن أن نختار شيئا أخف وزنا؟ نظريا ، يمكننا ، وهذا هو الفكر الجيد. ولكن دعونا نلقي نظرة على فئة الخوارزميات التي ينتمي إليها LZ4.
بادئ ذي بدء ، إنه عام ولا يتكيف مع نوع البيانات. على سبيل المثال ، إذا كنت تعلم مقدمًا أنه سيكون لديك مجموعة من الأعداد الصحيحة ، يمكنك استخدام إحدى خوارزميات VarInt وسيستخدم ذلك وحدة المعالجة المركزية بشكل أكثر فعالية. ثانياً ، LZ4 لا يعتمد بشكل مفرط على افتراضات طراز البيانات. لنفترض أن لديك سلسلة زمنية مرتبة من قيم المستشعر ، ومجموعة من أرقام الفاصلة العائمة. إذا أخذت هذا في الاعتبار ، يمكنك حساب الدلتا بين هذه الأرقام ثم ضغطها باستخدام خوارزمية عامة ، مما يؤدي إلى ارتفاع نسبة الضغط.
لن تواجه أي مشاكل عند استخدام LZ4 مع أي صفائف بايت أو أي ملفات. بالطبع لديه تخصص (أكثر على ذلك لاحقًا) ، وفي بعض الحالات يكون استخدامه بلا فائدة. ولكن إذا نسميها خوارزمية للأغراض العامة ، فسنكون قريبًا من الحقيقة. تجدر الإشارة إلى أنه بفضل التصميم الداخلي ، تقوم LZ4 تلقائيًا بتنفيذ خوارزمية
RLE كحالة خاصة.
ومع ذلك ، فإن السؤال الأكثر أهمية هو ما إذا كان LZ4 هو الخوارزمية المثلى لهذه الفئة من حيث السرعة الكلية وقوة الانضغاط. تُسمى الخوارزميات المثالية "حدود Pareto" ، مما يعني أنه لا توجد خوارزمية أخرى أفضل بشكل نهائي بطريقة أو بأخرى من أسوأ (بطرق واسعة ومتنوعة من مجموعات البيانات أيضًا). تكون بعض الخوارزميات أسرع ولكنها تؤدي إلى نسبة ضغط أصغر ، في حين أن البعض الآخر لديه ضغط أقوى ولكنه أبطأ في الضغط أو الضغط.
بصراحة ، ليست LZ4 حدود Pareto حقًا - فهناك بعض الخيارات المتاحة التي تعد أفضل قليلاً. على سبيل المثال ، انظر إلى
LZTURBO من مطور يطلق عليه اسم
powturbo . ليس هناك شك في موثوقية النتائج ، وذلك بفضل مجتمع
encode.ru (وهو أكبر منتدى على الأرجح وضغط البيانات). لسوء الحظ ، لا يقوم المطور بتوزيع التعليمات البرمجية المصدر أو الثنائيات. لا تتوفر إلا لعدد محدود من الأشخاص للاختبار ، أو مقابل الكثير من المال (على الرغم من أنه لا يبدو أن أحدا قد دفع ثمنها ، حتى الآن). يمكنك أيضًا إلقاء نظرة على
Lizard (LZ5 سابقًا)
والكثافة . قد تعمل بشكل أفضل قليلاً من LZ4 عند تحديد مستوى ضغط معين. خيار آخر مثير للاهتمام حقا هو
LZSSE . ولكن الانتهاء من قراءة هذه المقالة قبل التحقق من ذلك.
كيف يعمل LZ4
دعونا ننظر في كيفية عمل LZ4 بشكل عام. هذا أحد تطبيقات خوارزمية LZ77. تمثل L و Z أسماء المطورين (Lempel و Ziv) ، و 77 هو عام 1977 عندما تم نشر الخوارزمية. لديها العديد من التطبيقات الأخرى: QuickLZ و FastLZ و BriefLZ و LZF و LZO و gzip و zip إذا تم استخدام مستويات ضغط منخفضة.
تحتوي كتلة البيانات المضغوطة باستخدام LZ4 على سلسلة من الإدخالات (الأوامر أو التعليمات) من نوعين:
- حرفية: "خذ البايتات N التالية كما هي وانسخها إلى النتيجة".
- المطابقة: "خذ N بايت من النتيجة التي تم فك ضغطها بدءًا من قيمة الإزاحة بالنسبة للموضع الحالي".
المثال. قبل الضغط:
Hello world Hello
بعد الضغط:
literals 12 "Hello world " match 5 12
إذا أخذنا كتلة مضغوطة وكررنا المؤشر خلاله أثناء تشغيل هذه الأوامر ، فسنحصل على البيانات غير المضغوطة الأصلية كنتيجة لذلك.
لذلك هذا هو الأساس كيف يتم إلغاء ضغط البيانات. الفكرة الأساسية واضحة: لإجراء الضغط ، تقوم الخوارزمية بترميز تسلسل متكرر من وحدات البايت باستخدام التطابقات.
بعض الخصائص واضحة أيضا. هذه الخوارزمية الموجهة نحو البايت لا تشريح البايتات الفردية ؛ انها فقط نسخها في مجملها. هذه هي الطريقة التي يختلف عن ترميز الانتروبيا. على سبيل المثال ،
zstd عبارة عن مزيج من LZ77 وترميز إنتروبي.
لاحظ أنه يجب ألا يكون حجم الكتلة المضغوطة كبيرًا جدًا. يتم اختيار الحجم لتجنب إهدار الكثير من ذاكرة الوصول العشوائي أثناء إلغاء الضغط ، لتجنب إبطاء الوصول العشوائي أكثر من اللازم في الملف المضغوط (الذي يتكون من عدد كبير من الكتل المضغوطة) ، وأحيانًا حتى يتم احتواء الكتلة في ذاكرة التخزين المؤقت CPU. على سبيل المثال ، يمكنك اختيار 64 كيلو بايت بحيث يتم احتواء المخازن المؤقتة للبيانات المضغوطة وغير المضغوطة في ذاكرة التخزين المؤقت L2 مع نصف ما زال مجانيًا.
إذا احتجنا إلى ضغط ملف أكبر ، يمكننا توصيل الكتل المضغوطة. هذا أيضًا مناسب لتخزين بيانات إضافية (مثل المجموع الاختباري) مع كل كتلة مضغوطة.
الحد الأقصى للتعويض عن المباراة محدود. في LZ4 ، الحد الأقصى هو 64 كيلو بايت. هذا المبلغ يسمى النافذة المنزلقة. هذا يعني أنه يمكن العثور على التطابقات في نافذة من 64 كيلو بايت تسبق المؤشر ، والذي ينزلق مع المؤشر أثناء تحركه للأمام.
الآن لنلقِ نظرة على كيفية ضغط البيانات ، أو بمعنى آخر ، كيفية العثور على تسلسلات مطابقة في ملف. يمكنك دائمًا استخدام اللاحقة (إنه أمر رائع إذا كنت قد سمعت بهذا بالفعل). هناك طرق تضمن وجود أطول تطابق في البايتات السابقة بعد الضغط. يُسمى هذا التحليل الأمثل ويوفر أفضل نسبة ضغط تقريبًا للكتلة المضغوطة ذات التنسيق الثابت. ولكن هناك طرقًا أفضل ، مثل العثور على تطابق جيد بما يكفي ليس بالضرورة الأطول. الطريقة الأكثر فاعلية للعثور عليه هي استخدام جدول التجزئة.
للقيام بذلك ، نقوم بتكرار المؤشر من خلال كتلة البيانات الأصلية ونأخذ بضع بايتات بعد المؤشر (دعنا نقول 4 بايت). نقوم بتجميعها ووضع الإزاحة من بداية الكتلة (حيث تم نقل وحدات البايت الأربع) في جدول التجزئة. تسمى القيمة 4 "min-match" - باستخدام جدول التجزئة هذا ، يمكننا العثور على تطابقات لا تقل عن 4 بايت.
إذا نظرنا إلى جدول التجزئة وله بالفعل سجل مطابق ، ولم يتجاوز الإزاحة النافذة المنزلق ، فإننا نتحقق لمعرفة عدد البايتات الإضافية التي تتطابق بعد تلك البايتات الأربعة. ربما هناك الكثير من المباريات. من الممكن أيضًا أن يكون هناك تصادم في جدول التجزئة ولا يوجد شيء مطابق ، لكن هذه ليست مشكلة كبيرة. يمكنك فقط استبدال القيمة في جدول التجزئة بآخر جديد. سوف يؤدي التصادم في جدول التجزئة ببساطة إلى انخفاض نسبة الضغط ، حيث سيكون هناك عدد أقل من التطابقات. بالمناسبة ، يسمى هذا النوع من جدول التجزئة (بحجم ثابت وبدون أي تصادم) "جدول ذاكرة التخزين المؤقت". هذا الاسم منطقي لأنه في حالة حدوث تصادم ، ينسى جدول ذاكرة التخزين المؤقت ببساطة الإدخال القديم.
تحد للقارئ الدقيق. لنفترض أن البيانات عبارة عن صفيف من أرقام UInt32 بتنسيق داخلي صغير يمثل جزءًا من سلسلة من الأرقام الطبيعية: 0 ، 1 ، 2 ... اشرح لماذا لا يتم ضغط هذه البيانات عند استخدام LZ4 (حجم البيانات المضغوطة ليس أصغر مقارنةً بالبيانات غير المضغوطة).
كيفية تسريع كل شيء
لذلك أريد أن تسريع LZ4 الضغط. دعونا نرى كيف تبدو حلقة الضغط. ومن هنا في الكود الكاذب:
while (...) { read(input_pos, literal_length, match_length); copy(output_pos, input_pos, literal_length); output_pos += literal_length; read(input_pos, match_offset); copy(output_pos, output_pos - match_offset, match_length); output_pos += match_length; }
تم تصميم تنسيق LZ4 بحيث تتوافق القيم الحرفية والمطابقات في ملف مضغوط. من الواضح أن الحرفي يأتي دائمًا أولاً (لأنه لا يوجد مكان للعب مباراة من البداية). لذلك ، يتم ترميز أطوالها معًا.
انها في الواقع أكثر تعقيدا قليلا من ذلك. تتم قراءة بايت واحد من الملف ، ثم يتم تقسيمه إلى قسمين (نصف بايت) يحتوي على الأرقام المشفرة من 0 إلى 15. إذا كان الرقم المقابل ليس 15 ، فمن المفترض أن يكون طول الحرفي والمطابقة ، على التوالي. وإذا كان الرقم 15 ، يكون الطول أطول ويتم ترميزه بالبايتات التالية. ثم يتم قراءة البايت التالي ، وتتم إضافة قيمته إلى الطول. إذا كان يساوي 255 ، يتم تنفيذ نفس الشيء مع البايت التالي.
لاحظ أن الحد الأقصى لنسبة الضغط لتنسيق LZ4 لا يصل إلى 255. وهناك ملاحظة أخرى عديمة الفائدة وهي أنه إذا كانت بياناتك زائدة عن الحاجة ، فإن استخدام LZ4 مرتين سيؤدي إلى تحسين نسبة الضغط.
عندما نقرأ طول الحرف (ثم طول المطابقة وإزاحة المطابقة) ، فإن مجرد نسخ كتلتين من الذاكرة يكفي لإلغاء ضغطه.
كيفية نسخ كتلة الذاكرة
يبدو أنه يمكنك فقط استخدام وظيفة
memcpy ، المصممة لنسخ كتل الذاكرة. لكن هذا ليس هو النهج الأمثل وغير المناسب حقًا.
استخدام memcpy ليس هو الأمثل لأنه:
- عادةً ما تكون موجودة في مكتبة libc (وعادةً ما تكون مكتبة libc مرتبطة ديناميكيًا ، لذلك سيتم إجراء مكالمة memcpy بشكل غير مباشر عبر PLT).
- لا يتم تضمينه بواسطة برنامج التحويل البرمجي إذا كانت وسيطة الحجم غير معروفة في وقت الترجمة.
- يبذل الكثير من الجهد لمعالجة مخلفات كتلة الذاكرة بشكل صحيح والتي ليست مضاعفات لطول كلمة الجهاز أو التسجيل.
النقطة الأخيرة هي الأكثر أهمية. لنفترض أننا طلبنا من وظيفة memcpy نسخ 5 بايت بالضبط. سيكون من الرائع نسخ 8 بايت على الفور ، باستخدام إرشادات movq.
Hello world Hello wo ...
^^^^^ ^^^ - src
^^^^^ ^^^ - dstولكن بعد ذلك سنقوم بنسخ ثلاث بايتات إضافية ، لذلك سنكتب خارج الحدود العازلة. لا تملك وظيفة
memcpy الإذن للقيام بذلك ، لأنها يمكن أن تستبدل بعض البيانات في برنامجنا وتؤدي إلى خلل في الذاكرة. وإذا كتبنا إلى عنوان غير محاذٍ ، فإن هذه البايتات الإضافية يمكن أن تهبط على صفحة غير مخصصة من الذاكرة الظاهرية أو على صفحة بدون حق الوصول للكتابة. من شأنها أن تعطينا خطأ تجزئة (هذا أمر جيد).
ولكن في حالتنا ، يمكننا دائمًا كتابة بايتات إضافية. يمكننا قراءة وحدات البايت الإضافية في مخزن الإدخال المؤقت طالما توجد وحدات البايت الإضافية بالكامل داخلها. في ظل نفس الظروف ، يمكننا كتابة البايتات الإضافية إلى المخزن المؤقت للإخراج ، لأننا سنستمر في الكتابة عليها في التكرار التالي.
هذا التحسين موجود بالفعل في التطبيق الأصلي لـ LZ4:
inline void copy8(UInt8 * dst, const UInt8 * src) { memcpy(dst, src, 8); /// Note that memcpy isn't actually called here. } inline void wildCopy8(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) { do { copy8(dst, src); dst += 8; src += 8; } while (dst < dst_end); }
للاستفادة من هذا التحسين ، نحتاج فقط إلى التأكد من أننا بعيدون بما فيه الكفاية عن الحدود العازلة. لا ينبغي أن يكلف هذا أي شيء ، لأننا نتحقق بالفعل من تجاوز سعة المخزن المؤقت. ومعالجة البايتات القليلة الماضية ، بيانات "بقايا" ، يمكن القيام به بعد الحلقة الرئيسية.
ومع ذلك ، لا تزال هناك بعض الفروق الدقيقة. يحدث النسخ مرتين في الحلقة: مع حرفي ومباراة. ومع ذلك ، عند استخدام الدالة
LZ4_decompress_fast (بدلاً من
LZ4_decompress_safe ) ، يتم إجراء التحقق مرة واحدة فقط ، عندما نحتاج إلى نسخ الحرفي. لا يتم إجراء التحقق عند نسخ المطابقة ، ولكن
مواصفات تنسيق LZ4 لها شروط تسمح لك
بتجنبه :
البايت الخمس الأخيرة هي دائمًا حرفية.
يجب أن تبدأ المطابقة الأخيرة 12 بايت على الأقل قبل نهاية الكتلة.
وبالتالي ، لا يمكن ضغط كتلة بها أقل من 13 بايت.
قد تؤدي بيانات الإدخال المحددة بشكل خاص إلى تلف الذاكرة. إذا كنت تستخدم وظيفة
LZ4_decompress_fast ، فأنت بحاجة إلى الحماية من البيانات السيئة. على الأقل ، يجب عليك حساب المجموع الاختباري للبيانات المضغوطة. إذا كنت بحاجة إلى الحماية من المتسللين ،
LZ4_decompress_safe الدالة
LZ4_decompress_safe . خيارات أخرى: خذ وظيفة تجزئة التشفير كاختباري (على الرغم من أن هذا من المحتمل أن يدمر الأداء) ؛ تخصيص المزيد من الذاكرة للمخازن المؤقتة ؛ تخصيص ذاكرة للمخازن المؤقتة مع استدعاء
mmap منفصل وإنشاء صفحة حماية.
عندما أرى رمزًا يقوم بنسخ 8 بايتات من البيانات ، أتساءل على الفور لماذا بالضبط 8 بايت. يمكنك نسخ 16 بايت باستخدام سجلات SSE:
inline void copy16(UInt8 * dst, const UInt8 * src) { #if __SSE2__ _mm_storeu_si128(reinterpret_cast<__m128i *>(dst), _mm_loadu_si128(reinterpret_cast<const __m128i *>(src))); #else memcpy(dst, src, 16); #endif } inline void wildCopy16(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) { do { copy16(dst, src); dst += 16; src += 16; } while (dst < dst_end); }
نفس الشيء يعمل لنسخ 32 بايت ل AVX و 64 بايت ل AVX-512. بالإضافة إلى ذلك ، يمكنك إزالة الحلقة عدة مرات. إذا كنت قد نظرت من أي وقت مضى في كيفية تنفيذ
memcpy ، فهذا هو بالضبط النهج المستخدم. (بالمناسبة ، لن يقوم برنامج التحويل البرمجي بإلغاء أو تحويل الحلقة في هذه الحالة ، لأن هذا سيتطلب إدراج اختبارات ضخمة.)
لماذا لم تنفيذ LZ4 الأصلي القيام بذلك؟ أولاً ، ليس من الواضح ما إذا كان هذا أفضل أم أسوأ. يعتمد الربح الناتج على حجم الكتل المراد نسخها ، لذلك إذا كانت جميعها قصيرة ، فسيكون ذلك إنشاء عمل إضافي مقابل لا شيء. وثانيا ، إنه يدمر الأحكام في تنسيق LZ4 التي تساعد على تجنب فرع غير ضروري في الحلقة الداخلية.
ومع ذلك ، سنضع هذا الخيار في الاعتبار في الوقت الحالي.
نسخ صعبة
دعنا نعود إلى مسألة ما إذا كان من الممكن دائمًا نسخ البيانات بهذه الطريقة. دعنا نقول أننا بحاجة إلى نسخ مطابقة ، أي أخذ قطعة من الذاكرة من المخزن المؤقت الإخراج الموجود في إزاحة بعض خلف المؤشر ونسخها إلى موضع المؤشر.
تخيل حالة بسيطة عندما تحتاج إلى نسخ 5 بايت في إزاحة 12:
Hello world ...........
^^^^^ - src
^^^^^ - dst
Hello world Hello wo ...
^^^^^ - src
^^^^^ - dstولكن هناك حالة أكثر صعوبة ، عندما نحتاج إلى نسخ كتلة من الذاكرة أطول من الإزاحة. بمعنى آخر ، يتضمن بعض البيانات التي لم تتم كتابتها بعد إلى المخزن المؤقت للإخراج.
نسخ 10 بايت في إزاحة 3:
abc .............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst
abc abcabcabca ...
^^^^^^^^^^ - src
^^^^^^^^^^ - dstلدينا جميع البيانات أثناء عملية الضغط ، ويمكن العثور على مثل هذه المطابقة. وظيفة
memcpy ليست مناسبة لنسخها ، لأنها لا تدعم الحالة عندما تتداخل نطاقات كتل الذاكرة. لن تعمل وظيفة
memmove أيضًا ، لأن كتلة الذاكرة التي يجب أخذ البيانات منها لم تتم تهيئتها بالكامل بعد. نحن بحاجة إلى نسخ بالطريقة نفسها كما لو كنا نسخ بايت بايت.
op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; ...
إليك كيف تعمل:
a bc a ............
^ - src
^ - dst
a b ca b ...........
^ - src
^ - dst
ab c ab c ..........
^ - src
^ - dst
abc a bc a .........
^ - src
^ - dst
abca b ca b ........
^ - src
^ - dstبمعنى آخر ، يجب علينا إنشاء تسلسل متكرر. استخدم التطبيق الأصلي لـ LZ4 بعض التعليمات البرمجية الغريبة بشكل مدهش للقيام بذلك:
const unsigned dec32table[] = {0, 1, 2, 1, 4, 4, 4, 4}; const int dec64table[] = {0, 0, 0, -1, 0, 1, 2, 3}; const int dec64 = dec64table[offset]; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += dec32table[offset]; memcpy(op+4, match, 4); match -= dec64;
يقوم بنسخ البايتات الأربعة الأولى واحدة تلو الأخرى ، يتخطى بعض الأرقام السحرية ، وينسخ البايتات الأربعة التالية بالكامل ، وينقل المؤشر إلى تطابق باستخدام رقم سحري آخر. نسي مؤلف الكود (
Yan Collet ) بطريقة ما ترك تعليق حول معنى هذا. بالإضافة إلى ذلك ، أسماء متغير مربكة. كلاهما يدعى dec ... table ، ولكن يتم إضافة واحد والآخر يتم طرحه. بالإضافة إلى ذلك ، أحدهما غير موقّع ، والآخر int. ومع ذلك ، قام المؤلف مؤخرًا بتحسين هذا المكان في الكود.
وإليك كيف يعمل في الواقع. نقوم بنسخ أول 4 بايت واحد في كل مرة:
abc abca .........
^^^^ - src
^^^^ - dstالآن يمكننا نسخ 4 بايت في وقت واحد:
abcabca bcab .....
^^^^ - src
^^^^ - dstيمكننا المتابعة كالمعتاد ، ونسخ 8 بايت في وقت واحد:
abcabcabcab cabcabca .....
^^^^^^^^ - src
^^^^^^^^ - dstكما نعلم جميعًا من التجربة ، فإن أفضل طريقة لفهم الكود هي في بعض الأحيان إعادة كتابتها. إليك ما توصلنا إليه:
inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset) { /// 4 % n. /// Or if 4 % n is zero, we use n. /// It gives an equivalent result, but is more CPU friendly for unknown reasons. static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 }; /// 8 % n - 4 % n static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 }; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += shift1[offset]; memcpy(op + 4, match, 4); match += shift2[offset]; }
كما هو متوقع ، هذا لا يغير الأداء على الإطلاق. أردت حقًا تجربة التحسين لنسخ 16 بايت في آن واحد.
ومع ذلك ، يؤدي هذا إلى تعقيد "الحالة الخاصة" ويتسبب في استدعاءها أكثر من مرة (يتم تنفيذ شرط
offset < 16 على الأقل بقدر
offset < 8 ). يبدو نسخ النطاقات المتداخلة مع النسخ ذات 16 بايت كما يلي (فقط البداية الموضحة):
inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset) { /// 4 % n. static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 }; /// 8 % n - 4 % n static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 }; /// 16 % n - 8 % n static constexpr int shift3[] = { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 }; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += shift1[offset]; memcpy(op + 4, match, 4); match += shift2[offset]; memcpy(op + 8, match, 8); match += shift3[offset]; }
هل يمكن تنفيذ هذه الوظيفة بشكل أكثر فعالية؟ نود أن نجد تعليمات SIMD سحرية لهذه الشفرة المعقدة ، لأن كل ما نريد القيام به هو كتابة 16 بايت ، والتي تتكون بالكامل من بضع بايتات من بيانات الإدخال (من 1 إلى 15). ثم يحتاجون فقط أن تتكرر بالترتيب الصحيح.
هناك تعليمات مثل هذا تسمى
pshufb (بايت خلط ورق اللعب المعبأ) التي تعد جزءًا من SSSE3 (ثلاث S). يقبل تسجيلين 16 بايت. أحد السجلات يحتوي على البيانات المصدر. الآخر لديه "محدد": كل بايت يحتوي على رقم من 0 إلى 15 ، وهذا يتوقف على أي بايت من سجل المصدر للحصول على النتيجة من. إذا كانت قيمة البايت المحدد أكبر من 127 ، يتم ملء البايتة المقابلة للنتيجة بصفر.
هنا مثال:
xmm0: abc .............
xmm1: 0120120120120120
pshufb٪ xmm1 ،٪ xmm0
xmm0: abcabcabcabcabca
كل بايتة من النتيجة مليئة بالبايت المحدد من البيانات المصدر - هذا هو بالضبط ما نحتاجه! إليك ما يبدو عليه الرمز في النتيجة:
inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset) { #ifdef __SSSE3__ static constexpr UInt8 __attribute__((__aligned__(16))) masks[] = { 0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0, }; _mm_storeu_si128(reinterpret_cast<__m128i *>(op), _mm_shuffle_epi8( _mm_loadu_si128(reinterpret_cast<const __m128i *>(match)), _mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset))); match += masks[offset]; #else copyOverlap16(op, match, offset); #endif }
هنا
_mm_shuffle_epi8 هو
جوهري ، والذي يجمع إلى تعليمات
pshufb CPU.
هل يمكننا إجراء هذه العملية لمزيد من وحدات البايت في وقت واحد باستخدام إرشادات أحدث؟ بعد كل شيء ، SSSE3 عبارة عن مجموعة تعليمات قديمة جدًا موجودة منذ عام 2006. AVX2 بها تعليمة تقوم بذلك بـ 32 بايت في آن واحد ، ولكن بشكل منفصل لممرات 16 بايت الفردية. يسمى هذا بالبايت بيرميت المتجه ، بدلاً من البايتات المختلطة المعبأة - الكلمات مختلفة ، لكن المعنى هو نفسه. يحتوي AVX-512 VBMI على تعليمات أخرى تعمل مع 64 بايت في آن واحد ، لكن المعالجات التي تدعمها لم تظهر إلا مؤخرًا. يحتوي ARM NEON على إرشادات مشابهة تسمى vtbl (بحث جدول المتجهات) ، لكنها تسمح فقط بكتابة 8 بايت.
بالإضافة إلى ذلك ، هناك إصدار من تعليمات
pshufb مع سجلات MMX 64 بت من أجل تشكيل 8 بايت. إنه مناسب تمامًا لاستبدال النسخة الأصلية من الكود. ومع ذلك ، قررت استخدام خيار 16 بايت بدلاً من ذلك (لأسباب خطيرة).
في مؤتمر Highload ++ Siberia ، حضرني أحد الحضور بعد عرضي التقديمي وذكر أنه بالنسبة لحالة 8 بايت ، يمكنك فقط استخدام الضرب بواسطة ثابت تم اختياره بشكل خاص (ستحتاج أيضًا إلى إزاحة) - هذا لم يحدث حتى لي من قبل!
كيفية إزالة زائدة إذا البيان
لنفترض أنني أريد استخدام متغير ينسخ 16 بايت. كيف يمكنني تجنب الاضطرار لإجراء فحص إضافي لتجاوز سعة المخزن المؤقت؟
قررت أنني فقط لن أفعل هذا الاختيار. ستشير التعليقات على الوظيفة إلى أنه يجب على المطور تخصيص كتلة من الذاكرة لعدد معين من البايتات أكثر مما هو مطلوب ، حتى نتمكن من قراءة وكتابة البيانات المهملة غير الضرورية هناك. سيكون من الصعب استخدام واجهة الوظيفة ، لكن هذه مشكلة مختلفة.
في الواقع ، قد تكون هناك عواقب سلبية. دعنا نقول أن البيانات التي نحتاج إلى فك ضغطها تم تشكيلها من كتل تبلغ 65536 بايت لكل منها. ثم يعطينا المستخدم قطعة من الذاكرة تبلغ 65.536 بايت للبيانات التي تم فك ضغطها. ولكن مع واجهة الوظيفة الجديدة ، سيُطلب من المستخدم تخصيص كتلة ذاكرة تبلغ 65،551 بايت ، على سبيل المثال. ثم قد يضطر التخصيص إلى تخصيص 96 أو حتى 128 كيلو بايت ، اعتمادًا على تنفيذه. إذا كان التخصيص سيئًا جدًا ، فقد يتوقف التخزين المؤقت للذاكرة بشكل مفاجئ في "الكومة" ويبدأ في استخدام
mmap و
munmap كل مرة لتخصيص الذاكرة (أو
madvice الذاكرة باستخدام
madvice ). ستكون هذه العملية بطيئة للغاية بسبب أخطاء الصفحة. نتيجة لذلك ، قد ينتهي هذا التحسين البسيط بإبطاء كل شيء.
هل هناك أي تسارع؟
لذلك قمت بعمل نسخة من الكود الذي يستخدم ثلاثة تحسينات:
- نسخ 16 بايت بدلاً من 8.
- باستخدام تعليمات خلط ورق اللعب
offset < 16 حالة. - إزالة واحد إضافي إذا.
بدأت اختبار هذا الرمز على مجموعات مختلفة من البيانات وحصلت على نتائج غير متوقعة.
مثال 1:
زيون E2650v2 ، بيانات متصفح Yandex ، عمود AppVersion.
المرجع: 1.67 جيجابايت / ثانية.
16 بايت ، خلط ورق اللعب: 2.94 جيجابايت / ثانية (76٪ أسرع).
مثال 2:
زيون E2650v2 ، ياندكس المباشر البيانات ، العمود ShowsSumPosition.
المرجع: 2.30 جيجابايت / ثانية.
16 بايت ، خلط ورق اللعب: 1.91 جيجابايت / ثانية (20٪ أبطأ).
كنت سعيدًا حقًا في البداية ، عندما رأيت أن كل شيء قد تسارع بمعدل كبير. ثم رأيت أن لا شيء كان أسرع مع الملفات الأخرى. كان أبطأ قليلاً بالنسبة للبعض منهم. خلصت إلى أن النتائج تعتمد على نسبة الضغط. كلما زاد ضغط الملف ، زادت الاستفادة من التبديل إلى 16 بايت. هذا شعور طبيعي: كلما زادت نسبة الضغط ، زاد متوسط طول الأجزاء المراد نسخها.
للتحقيق ، استخدمت قوالب C ++ لإنشاء خيارات تعليمات برمجية لأربع حالات: استخدام مجموعات ذات 8 بايت أو 16 بايت ، مع أو بدون تعليمة خلط ورق اللعب.
template <size_t copy_amount, bool use_shuffle> void NO_INLINE decompressImpl( const char * const source, char * const dest, size_t dest_size)
كان أداء المتغيرات المختلفة تمامًا للشفرة أفضل على ملفات مختلفة ، ولكن عند الاختبار على سطح المكتب ، فستظل النسخة التي يتم خلطها دائمًا دائمًا. الاختبار على سطح المكتب غير مريح لأن عليك القيام بذلك:
sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium)
ثم انتقلت إلى أحد خوادم "التطوير" القديمة (مع معالج Xeon E5645) ، واستولت على المزيد من مجموعات البيانات ، وحصلت على نتائج معاكسة تقريبًا ، الأمر الذي أربكني تمامًا. اتضح أن اختيار الخوارزمية الأمثل يعتمد على طراز المعالج ، بالإضافة إلى نسبة الضغط. يحدد المعالج متى يكون من الأفضل استخدام تعليمة خلط ورق اللعب ، بالإضافة إلى عتبة تحديد موعد بدء استخدام النسخ ذات 16 بايت.
بالمناسبة ، عند الاختبار على خوادمنا ، من المنطقي القيام بذلك:
sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client)
خلاف ذلك ، فإن النتائج ستكون غير مستقرة. احترس أيضًا من الاختناق الحراري ووضع حد أقصى للطاقة.
كيفية اختيار أفضل الخوارزمية
لذلك لدينا أربعة أنواع من الخوارزمية ونحتاج إلى اختيار أفضل خيار للظروف. يمكننا إنشاء مجموعة تمثيلية من البيانات والأجهزة ، ثم إجراء اختبار جاد للحمل واختيار الطريقة الأفضل في المتوسط. لكن ليس لدينا مجموعة بيانات تمثيلية. لاختبار ، استخدمت عينة من البيانات من
Yandex Metrica و Yandex Direct و Yandex Browser
والرحلات الجوية في الولايات المتحدة . لكن هذا لا يكفي ، لأن ClickHouse تستخدمه مئات الشركات في جميع أنحاء العالم. من خلال الإفراط في التحسين على مجموعة بيانات واحدة ، قد نتسبب في انخفاض الأداء مع البيانات الأخرى وحتى لا ندرك ذلك. وإذا كانت النتائج تعتمد على طراز المعالج ، فسنضطر إلى كتابة الشروط في الشفرة بشكل صريح واختبارها على كل طراز (أو الرجوع إلى الدليل المرجعي بشأن تعليمات التوقيت ، ما رأيك؟). في كلتا الحالتين ، هذا هو مضيعة للوقت للغاية.
لذلك قررت استخدام طريقة أخرى ، وهو أمر واضح للزملاء الذين درسوا في كلية تحليل البيانات لدينا:
"قطاع الطرق متعدد الأسلحة" . النقطة المهمة هي أن متغير الخوارزمية يتم اختياره عشوائيًا ، ثم نستخدم الإحصائيات بشكل تدريجي لاختيار الخيارات التي تعمل بشكل أفضل.
لدينا العديد من كتل البيانات التي تحتاج إلى فك الضغط ، لذلك نحن بحاجة إلى استدعاءات الوظائف المستقلة لإلغاء ضغط البيانات. يمكننا اختيار واحدة من الخوارزميات الأربع لكل كتلة وقياس وقت تنفيذها. عادةً لا تكلف عملية كهذه شيئًا بالمقارنة مع معالجة كتلة من البيانات ، وفي ClickHouse تبلغ كتلة البيانات غير المضغوطة 64 كيلو بايت على الأقل. (اقرأ هذا
المقال حول قياس الوقت.)
للحصول على فهم أفضل لكيفية عمل خوارزمية "قطاع الطرق متعدد السلاح" ، دعونا نلقي نظرة على مصدر الاسم. هذا تشبيه بآلات القمار في الكازينو التي تحتوي على عدة أدوات يمكن للاعب سحبها للحصول على مبلغ عشوائي من المال. يمكن للاعب سحب الرافعات عدة مرات بأي ترتيب. كل ذراع لديه احتمال ثابت للمبلغ المقابل من الأموال المقدمة ، ولكن اللاعب لا يعرف كيف يعمل ويمكن أن يتعلم فقط من تجربة لعب اللعبة. بمجرد معرفة ذلك ، يمكنهم زيادة أرباحهم إلى الحد الأقصى.
تتمثل إحدى الطرق لتعظيم المكافأة في تقييم توزيع الاحتمالات لكل رافعة في كل خطوة بناءً على إحصائيات اللعبة من الخطوات السابقة. ثم "عقليا" نربح مكافأة عشوائية لكل رافعة ، بناءً على التوزيعات المستلمة. أخيرًا ، نجذب الرافعة التي حققت أفضل النتائج في لعبتنا العقلية. هذا النهج يسمى طومسون أخذ العينات.
لكننا نختار خوارزمية تخفيف الضغط. والنتيجة هي وقت التنفيذ بالبكو ثانية لكل بايت: كلما كان ذلك أفضل ، كلما كان ذلك أفضل. سننظر في وقت التنفيذ كمتغير عشوائي وتقييم توزيعه باستخدام الإحصاءات الرياضية. غالبًا ما يتم استخدام نهج Bayesian لمهام مثل هذا ، ولكن سيكون من الصعب إدخال صيغ معقدة في رمز C ++. يمكننا استخدام نهج حدودي ونقول أن متغير عشوائي ينتمي إلى عائلة حدودي من المتغيرات العشوائية ، ومن ثم تقييم المعلمات.
كيف نختار عائلة المتغيرات العشوائية؟ كمثال ، قد نفترض أن وقت تنفيذ التعليمات البرمجية له توزيع طبيعي. لكن هذا خاطئ تماما. أولاً ، لا يمكن أن يكون وقت التنفيذ سالبًا ، والتوزيع العادي يأخذ قيمًا في كل مكان على خط الأرقام. ثانياً ، أفترض أن وقت التنفيذ سيكون له "ذيل" ثقيل على الطرف الأيمن.
ومع ذلك ، هناك عوامل يمكن أن تجعل من المستحسن تقدير التوزيع الطبيعي فقط لأغراض أخذ Thompson Sampling (على الرغم من أن توزيع المتغير المستهدف ليس طبيعيًا بالضرورة). والسبب في ذلك هو أنه من السهل جدًا حساب التوقع الرياضي والتباين ، وبعد عدد كاف من التكرارات ، يصبح التوزيع الطبيعي ضيقًا إلى حد ما ، لا يختلف كثيرًا عن التوزيعات التي كنا سنحصل عليها باستخدام طرق أخرى. إذا لم نكن مهتمين جدًا بمعدل التقارب في الخطوات الأولى ، فيمكن تجاهل هذه التفاصيل.
This may seem like a somewhat ignorant approach. Experience has shown us that the average time for query execution, website page loading, and so on is "garbage" that isn't worth calculating. It would be better to calculate the median, which is a
robust statistic . But this is a little more difficult, and as I will show later, the described method justifies itself for practical purposes.
At first I implemented calculation of the mathematical expectation and variance, but then I decided that this is too good, and I need to simplify the code to make it "worse":
/// For better convergence, we don't use proper estimate of stddev. /// We want to eventually separate the two algorithms even in cases /// when there is no statistical significant difference between them. double sigma() const { return mean() / sqrt(adjustedCount()); } double sample(pcg64 & rng) const { ... return std::normal_distribution<>(mean(), sigma())(rng); }
I wrote it so that the first few iterations were not taken into account, to eliminate the effect of memory latencies.
The result is a test program that can select the best algorithm for the input data, with optional modes that use the reference implementation of LZ4 or a specific version of the algorithm.
So there are six options:
— Reference (baseline): original LZ4 without our modifications.
— Variant 0: copy 8 bytes at a time without shuffle.
— Variant 1: copy 8 bytes at a time with shuffle.
— Variant 2: copy 16 bytes at a time without shuffle.
— Variant 3: copy 16 bytes at a time with shuffle.
— The "bandit" option, which selects the best of the four optimized variants.
Testing on different CPUs
If the result strongly depends on the CPU model, it would be interesting to find out exactly how it is affected. There might be an exceptionally large difference on certain CPUs.
I prepared a set of datasets from different tables in ClickHouse with real data, for a total of 256 different files each with 100 MB of uncompressed data (the number 256 was coincidental). Then I looked at the CPUs of the servers where I can run benchmarks. I found servers with the following CPUs:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz
The most interesting part comes next — the processors provided by the R&D department:
— AMD EPYC 7351 16-Core Processor, a new AMD server processor.
— Cavium ThunderX2, which is AArch64, not x86. For these, my SIMD optimization needed to be reworked a bit. The server has 224 logical and 56 physical cores.
There are 13 servers in total, and each of them runs the test on 256 files in 6 variants (reference, 0, 1, 2, 3, adaptive). The test is run 10 times, alternating between the options in random order. It outputs 199,680 results that we can compare.
For example, we can compare different CPUs with each other. But we shouldn't jump to conclusions from these results, because we are only testing the LZ4 decompression algorithm on a single core (this is a very narrow case, so we only get a micro-benchmark). For example, the Cavium has the lowest performance per single core. But I tested ClickHouse on it myself, and it wins out over Xeon E5-2650 v2 on heavy queries due to the greater number of cores, even though it is missing many optimizations that are made in ClickHouse specifically for the x86.
┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐
│ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │
│ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │
│ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │
│ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │
│ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │
│ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │
│ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │
│ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │
│ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │
└───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘
- ref, adapt, max — The speed in gigabytes per second (the value that is the reverse of the arithmetic mean of time for all launches on all datasets).
- best — The number of the best algorithm among the optimized variants, from 0 to 3.
- adapt_boost — The relative advantage of the adaptive algorithm compared to the baseline.
- max_boost — The relative advantage of the best of the non-adaptive variants compared to the baseline.
- adapt_over_max — The relative advantage of the adaptive algorithm over the best non-adaptive one.
The results show that we were able to speed up decompression by 12-20% on modern x86 processors. Even on ARM we saw 4% improvement, despite the fact that we didn't optimize much for this architecture. It is also clear that on average for different datasets, the "bandit" algorithm comes out ahead of the pre-selected best variant on all processors (except for very old Intel CPUs).
استنتاج
In practice, the usefulness of this work is dubious. Yes, LZ4 decompression was accelerated on average by 12-20%, and on some datasets the performance more than doubled. But in general, this doesn't have much effect on query execution time. It's difficult to find real queries that gain more than a couple percent in speed.
We decided to use ZStandard level 1 instead of LZ4 on several Yandex Metrica clusters intended for executing long queries, because it is more important to save IO and disk space on cold data. Keep this in mind if you have similar workload.
We observed the greatest benefits from optimizing decompression in highly compressible data, such as columns with mostly duplicate string values. However, we have developed a separate solution specifically for this scenario that allows us to significantly speed up queries over this kind of data.
Another point to remember is that optimization of decompression speed is often limited by the format of the compressed data. LZ4 uses a very good format, but Lizard, Density and LZSSE have other formats that can work faster. Perhaps instead of trying to accelerate LZ4, it would be better to just integrate LZSSE into ClickHouse.
It's unlikely that these optimizations will be implemented in the mainstream LZ4 library: in order to use them, the library interface would have to be modified. In fact, this is often the case with improving algorithms — optimizations don't fit into old abstractions and they have to be revised. However, variable names have already been corrected in the original implementation. For instance, inc and dec tables have been
corrected . In addition, about a month ago, the original implementation accelerated decompression by the same 12-15% by copying 32 bytes instead of 16, as discussed above. We tried the 32-byte option ourselves and the results were not that great, but they were still
faster .
If you look at the profile at the beginning of the article, you may notice that we could have removed one extra copying operation from the page cache to userspace (either using
mmap , or using
O_DIRECT and userspace page cache, but both options are problematic). We also could have slightly improved the checksum calculation (CityHash128 is currently used without CRC32-C, but we could use HighwayHash, FARSH or XXH3). Acceleration of these two operations is useful for weakly compressed data, since they are performed on compressed data.
In any case, the changes have already been added to master more than a year ago, and the ideas that resulted from this research have been applied in other tasks. You can also watch the
video from HighLoad++ Siberia, or view the
presentation (both in Russian).