خاصية التناظر لعلاقة التكامل المشترك

الغرض من هذه المقالة هو مشاركة النتائج المتناقضة في دراسة التكامل المشترك للسلسلة الزمنية : إذا كانت السلسلة الزمنية $$$دولا$ شارك متكامل مع قريب $$$B$ ، عدد $$$B$ لا تشارك دائما مع عدد $$$دولا$ .

إذا درسنا التكامل المشترك من الناحية النظرية البحتة ، فمن السهل أن تثبت أنه إذا كانت هذه السلسلة $$$دولا$ شارك في التكامل مع $$$B$ ثم صف $$$B$ شارك في التكامل مع $$$دولا$ . ومع ذلك ، إذا بدأنا في دراسة التكامل المشترك بشكل تجريبي ، اتضح أن الحسابات النظرية لم يتم تأكيدها دائمًا. لماذا يحدث هذا؟

تناظر

موقف $$$دولا$ دعا متماثل إذا $$$A \ subseteq A ^ {- 1}$ حيث $$$A ^ {- 1}$ - النسبة العكسية التي تحددها الحالة: $$$x A ^ {- 1} y$ بمثابة $$$yAx$ . وبعبارة أخرى ، إذا كانت العلاقة $$$xAy$ ثم العلاقة $$$yAx$ .

النظر في اثنين $$$I (1)$ عدد من $$$x_t$ و $$$y_t$ . $$$t = 0 ، \ dots ، T$ . Cointegration هو متماثل إذا $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ يجذب $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ وهذا هو ، إذا كان وجود الانحدار المباشر يؤدي إلى وجود معكوس.

النظر في المعادلة $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ . $$$\ beta_1 \ neq 0$ . مبادلة الجانبين الأيسر والأيمن وطرح $$$\ varepsilon_ {1t}$ من كلا الجزأين: $$$\ beta_1 x_t = y_t - \ varepsilon_ {1t}$ . ل $$$\ beta_1 \ neq 0$ بحكم التعريف ، قسّم كلا الجزأين إلى $$$\ beta_1$ :

$$

$$x_t = \ frac {1} {\ beta_1} y_t - \ frac {\ varepsilon_ {1t}} {\ beta_1}.$$

استبدل $$$1 / \ beta_1$ في $$$\ beta_2$ و $$$- \ varepsilon_ {1t} / \ beta_1$ في $$$\ varepsilon_ {2t}$ نحن نحصل عليها $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ . لذلك ، علاقة التكامل المشترك متماثلة.

يتبع ذلك إذا كان المتغير $$$X$ مترابط مع متغير $$$Y$ ثم المتغير $$$Y$ يجب أن تكون متكاملة مع المتغير $$$X$ . ومع ذلك ، لا يؤكد اختبار التزاوج المشترك للزاوية مع Granle Granger دائمًا خاصية التناظر هذه ، نظرًا لأن المتغير في بعض الأحيان $$$Y$ غير مشترك متكامل مع متغير $$$X$ وفقا لهذا الاختبار.

لقد اختبرت خاصية التناظر على بيانات عام 2017 لمبادلات موسكو ونيويورك باستخدام اختبار Angle-Granger. كان هناك 7975 زوجًا من الأسهم المدمجة في بورصة موسكو. بالنسبة لـ 7731 (97٪) من الأزواج المدمجة ، تم تأكيد خاصية التناظر ، ولم يتم تأكيد خاصية التناظر على 244 (3٪).

كان هناك 140،903 زوجًا من الأسهم المدمجة في بورصة نيويورك. بالنسبة إلى 136586 (97٪) من الأزواج المدمجة ، تم تأكيد خاصية التناظر ، وبالنسبة لـ 4317 (3٪) من الأزواج المشتركة ، لم يتم تأكيد خاصية التناظر.

ترجمة

يمكن تفسير هذه النتيجة من خلال القوة المنخفضة واحتمال الخطأ العالي في النوع الثاني من اختبار ديكي فولر ، الذي يستند إليه اختبار Angle-Granger. احتمالية حدوث خطأ من النوع الثاني يمكن تدوينها بواسطة $$$\ beta = P (H_0 | H_1)$ ثم القيمة $$$1 - \ beta$ تسمى قوة الاختبار. لسوء الحظ ، فإن اختبار ديكي فولر غير قادر على التمييز بين السلاسل الزمنية غير الثابتة والقريبة من غير الثابتة.

ما هي سلسلة زمنية شبه مستقرة؟ النظر في السلسلة الزمنية $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ . سلسلة زمنية ثابتة هي سلسلة فيها $$$0 <\ phi <1$ . سلسلة زمنية غير ثابتة هي سلسلة فيها $$$\ phi = 1$ . سلسلة زمنية شبه غير مستقرة هي سلسلة فيها القيمة $$$\ phi$ قريب من واحد.

في حالة التسلسل الزمني شبه غير الثابت ، غالبًا ما نكون غير قادرين على رفض الفرضية الفارغة غير الثابتة. هذا يعني أن اختبار ديكي فولر ينطوي على مخاطر عالية لخطأ من النوع الثاني ، أي احتمال عدم رفض الفرضية الخاطئة.

اختبار KPSS

استجابة محتملة لضعف اختبار ديكي فولر هو اختبار KPSS ، الذي يدين اسمه بالأحرف الأولى من علماء Kvyatkovsky و Phillips و Schmidt و Sheen. على الرغم من أن النهج المنهجي لهذا الاختبار يختلف تمامًا عن منهج ديكي فولر ، إلا أنه ينبغي فهم الفرق الرئيسي في التقليب بين الفرضيات الفارغة والبديلة.

في اختبار KPSS ، تنص الفرضية الفارغة على أن السلاسل الزمنية ثابتة ، مقابل البديل عن وجود عدم ثابت. يمكن تحديد سلاسل زمنية شبه غير ثابتة ، والتي تم تحديدها غالبًا على أنها غير ثابتة باستخدام اختبار Dickey-Fuller ، بشكل صحيح على أنها ثابتة باستخدام اختبار KPSS.

ومع ذلك ، يجب أن ندرك أن أي نتائج للاختبار الإحصائي هي مجرد احتمالية ويجب عدم الخلط بينها وبين بعض الأحكام الحقيقية. هناك دائمًا احتمال غير صفري بأننا مخطئون. لهذا السبب ، يُقترح دمج نتائج اختبارات Dickey-Fuller و KPSS كاختبار مثالي لعدم الثبات.



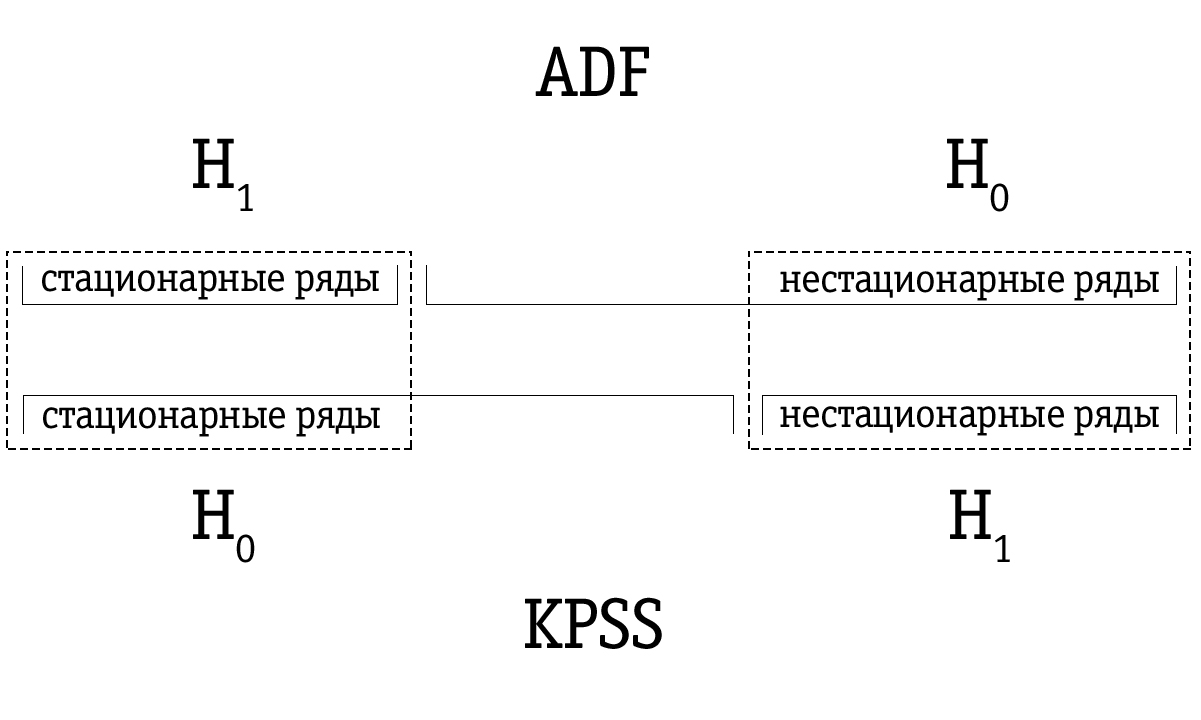
نظرًا لقلة الطاقة ، يحدد اختبار Dickey-Fuller في كثير من الأحيان عن طريق الخطأ السلسلة على أنها غير ثابتة ، وبالتالي فإن المجموعة الناتجة من السلاسل الزمنية المحددة في اختبار Dickey-Fuller أكبر من السلاسل الزمنية المحددة على أنها غير ثابتة باستخدام اختبار KPSS. لذلك ، أمر الاختبار مهم.

إذا تم تحديد السلسلة الزمنية على أنها ثابتة باستخدام اختبار Dickey-Fuller ، فمن المحتمل أيضًا تحديدها على أنها ثابتة باستخدام اختبار KPSS ؛ في هذه الحالة ، يمكننا أن نفترض أن السلسلة ثابتة بالفعل.

إذا تم تحديد السلسلة الزمنية على أنها غير مستقرة باستخدام اختبار KPSS ، فمن المحتمل أيضًا تحديدها على أنها غير مستقرة باستخدام اختبار Dickey-Fuller ؛ في هذه الحالة ، يمكننا أن نفترض أن المسلسل غير مستقر بالفعل.

ومع ذلك ، يحدث غالبًا أن سلسلة زمنية تم تحديدها على أنها غير ثابتة باستخدام اختبار Dickey-Fuller سيتم تمييزها على أنها ثابتة باستخدام اختبار KPSS. في هذه الحالة ، يجب أن نكون حذرين للغاية مع استنتاجنا النهائي. يمكننا التحقق من مدى قوة الأساس للثبات في حالة اختبار KPSS وعدم الثبات في حالة اختبار Dickey-Fuller واتخاذ قرار مناسب. بالطبع ، يمكننا أيضًا أن نترك مسألة جوهرية مثل هذه السلسلة الزمنية دون حل.

نهج اختبار KPSS يفترض سلسلة زمنية $$$y_t$ يمكن اختبار التحلل بالنسبة للثبات بالنسبة إلى الاتجاه إلى مجموع الاتجاه الحتمية $$$\ beta t$ المشي عشوائي $$$r_t$ والخطأ الثابت $$$\ varepsilon_t$ :

$$

$$y_t = \ beta t + r_t + \ varepsilon_t، \\ r_t = r_ {t-1} + u_t،$$

حيث $$$u_t$ - عملية iid طبيعية بمتوسط ​​صفر وتباين $$$\ سيجما ^ 2$ ( $$$u_t \ sim N (0، \ sigma ^ 2)$ ). القيمة الأولية $$$r_0$ يعامل على أنه ثابت ويلعب دور العضو الحر. خطأ ثابت $$$\ varepsilon_t$ يمكن أن تنشأ عن أي عملية ARMA مشتركة ، وهذا هو ، يمكن أن يكون لها ارتباط تلقائي قوي.

على غرار اختبار ديكي فولر ، القدرة على مراعاة بنية تعسفية من الارتباط التلقائي $$$\ varepsilon_t$ مهم للغاية لأن معظم السلاسل الزمنية الاقتصادية تعتمد بشكل كبير على الوقت وبالتالي يكون لها ارتباط قوي. إذا كنا نريد التحقق من المركزية فيما يتعلق المحور الأفقي ، ثم المصطلح $$$\ beta t$ مستبعد فقط من المعادلة أعلاه.

من المعادلة أعلاه يتبع ذلك الفرضية الفارغة $$$H_0 دولا$ عن المركزية $$$y_t$ أي ما يعادل الفرضية $$$\ sigma ^ 2 = 0$ ، الذي يتبع ذلك $$$r_t = r_0$ للجميع $$$t$ ( $$$r_0$ هو ثابت). وبالمثل ، فرضية بديلة $$$H_1$ عدم الاستقلالية يعادل الفرضية $$$\ sigma ^ 2 \ neq 0$ .

لاختبار الفرضية $$$H_0 دولا$ : $$$\ sigma ^ 2 = 0$ (سلسلة زمنية ثابتة) مقابل البديل $$$H_1$ : $$$\ sigma ^ 2 \ neq 0$ يتلقى مؤلفو اختبار KPSS (سلسلة زمنية غير ثابتة) إحصائيات أحادية الاتجاه لاختبار لاغرانج المضاعف. كما أنها تحسب توزيعها المقارب ونموذج القيم الحرجة المقارب. نحن لا نعتبر التفاصيل النظرية هنا ، ولكننا فقط نلخص لفترة وجيزة خوارزمية تنفيذ الاختبار.

عند إجراء اختبار KPSS لسلسلة زمنية $$$y_t$ . $$$t = 1 ، \ dots ، T$ يتم استخدام طريقة المربعات الصغرى (المربعات الصغرى) لتقدير إحدى المعادلات التالية:

$$

$$y_t = a_0 + \ varepsilon_t، \\ y_t = a_0 + \ beta t + \ varepsilon_t.$$

إذا كنا نريد التحقق من المركزية فيما يتعلق بالمحور الأفقي ، فإننا نقيم المعادلة الأولى. إذا كنا نخطط للتحقق من المركزية فيما يتعلق بالاتجاه ، فإننا نختار المعادلة الثانية.

أرصدة $$$e_t$ من المعادلة المقدرة تستخدم لحساب إحصائيات اختبار مضاعفات لاغرانج. يعتمد اختبار مضاعف لاجرانج على فكرة أنه عند تحقيق الفرضية الفارغة ، يجب أن تكون جميع مضاعفات لاجرانج مساوية للصفر.

اختبار لاجرانج المضاعف

يرتبط اختبار مضاعف لاجرانج بمقاربة أكثر عمومية لتقدير المعلمة باستخدام طريقة الاحتمالية القصوى (ML). وفقًا لهذا النهج ، تعتبر البيانات دليلًا على معايير التوزيع. يتم التعبير عن الدليل كدالة لمعلمات غير معروفة - دالة احتمالية:

$$

$$L (X_1 ، X_2 ، X_3 ، \ dots ، X_n ؛ \ Phi_1 ، \ Phi_2 ، \ dots ، \ Phi_k) ،$$

حيث $$$X_i$ هي القيم المرصودة ، و $$$\ Phi_i$ - المعلمات التي نريد تقييمها.

دالة الاحتمالية القصوى هي الاحتمال المشترك لملاحظات العينة.

$$

$$L (X_1 ، X_2 ، X_3 ، \ النقاط ، X_n ؛ \ Phi_1 ، \ Phi_2 ، \ dots ، \ Phi_k) = P (X_1 \ land X_2 \ land X_3 \ dots X_n).$$

الهدف من طريقة احتمال الحد الأقصى هو تحقيق أقصى قدر من وظيفة احتمال. يتم تحقيق ذلك عن طريق التمييز بين دالة الاحتمال القصوى لكل من المعلمات المقدرة ومساواة المشتقات الجزئية مع الصفر. قيم المعلمات التي تكون فيها قيمة الوظيفة هي الحد الأقصى هو التقدير المرغوب.

عادةً ، لتبسيط العمل اللاحق ، يتم أولاً أخذ لوغاريتم دالة الاحتمال.

النظر في نموذج خطي معمم $$$Y = \ beta X + \ varepsilon$ حيث يفترض ذلك $$$\ varepsilon$ وزعت عادة $$$N (0 ، \ sigma ^ 2)$ هذا هو $$$Y - \ beta X \ sim N (0، \ sigma ^ 2)$ .

نريد اختبار الفرضية القائلة بأن النظام $$$ف دولا$ ( $$$ف <ك$ ) القيود الخطية المستقلة $$$R \ beta = r$ . هنا $$$R$ - مشهور $$ مصفوفة رتبة $$$ف دولا$ و $$$ص$ - مشهور $$ النواقل.

لكل زوج من القيم المرصودة $$$X$ و $$$Y$ في ظل الظروف العادية ، سوف توجد وظيفة كثافة الاحتمال في النموذج التالي:

$$

$$f (X_i، Y_i) = \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

يخضع ل $$$ن$ الملاحظات المشتركة $$$X$ و $$$Y$ الاحتمال الكلي لمراقبة جميع القيم في العينة يساوي ناتج القيم الفردية لوظيفة كثافة الاحتمال. وبالتالي ، يتم تعريف وظيفة الاحتمال على النحو التالي:

$$

$$L (\ beta) = \ prod \ limit_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

نظرًا لأن التمييز بين المجموع أسهل من المنتج ، يتم عادةً أخذ لوغاريتم دالة الاحتمال ، وبالتالي:

$$

$$\ ln L (\ beta) = \ sum \ limit_ {i = 1} ^ n \ left (\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} - \ frac {1} { 2 \ sigma ^ 2} (Y_i - \ beta X_i) ^ 2 \ right).$$

هذا التحويل المفيد لا يؤثر على النتيجة النهائية ، لأن $$$\ Ln L$ هي وظيفة متزايدة $$$L$ . إذاً القيمة $$$\ beta$ مما يزيد $$$\ Ln L$ سوف تعظيم أيضا $$$L$ .

نتيجة ML ل $$$\ beta$ في الانحدار مع تقييد ( $$$R \ beta = r$ ) يتم الحصول عليها من خلال تعظيم الوظيفة $$$\ ln L (\ beta)$ يخضع ل $$$R \ beta = r$ . للعثور على هذا التقدير ، نكتب وظيفة Lagrange:

$$

$$\ psi (\ beta) = \ ln L (\ beta) - g '(R \ beta - r) ،$$

حيث من خلال $$$g = \ left (g_1 ، \ dots ، g_q \ right) '$ ناقلات ملحوظ $$$ف دولا$ مضاعفات لاجرانج.

لاجرانج اختبار إحصاءات المضاعف تدل على $$$\ eta_ \ mu$ في حالة الثبات فيما يتعلق بالمحور الأفقي ومن خلال $$$\ eta_ \ tau$ في حالة الثبات بالنسبة إلى الاتجاه ، يتم تحديده بواسطة التعبير

$$

$$\ eta _ {\ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2 (l)} \ sum \ limit_ {t = 1} ^ T S_t ^ 2 ،$$

حيث

$$

$$S_t = \ sum \ limit_ {i = 1} ^ t e_i$$

و

$$

$$s ^ 2 (l) = T ^ {- 1} \ sum \ limit_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {- 1} \ sum \ limit_ {1} ^ lw (s، l) \ sum \ limit_ {t = s + 1} ^ T e_t e_ {ts}،$$

حيث

$$

$$w (s، l) = 1 - \ frac {s} {l + 1}.$$

في المعادلات المذكورة أعلاه $$$S_t$ - عملية الأرصدة الجزئية $$$e_t$ من المعادلة المقدرة ؛ $$$s ^ 2 (l)$ - تقييم التشتت على المدى الطويل من المخلفات $$$e_t$ . و $$$w (s، l)$ - ما يسمى نافذة بارتليت الطيفية ، حيث $$$ل$ - تأخر اقتطاع المعلمة.

في هذا التطبيق ، يتم استخدام النافذة الطيفية لتقدير الكثافة الطيفية للأخطاء لفاصل زمني معين (نافذة) ، والذي يتحرك على طول النطاق الكامل للسلسلة. يتم تجاهل البيانات خارج الفاصل الزمني ، لأن وظيفة النافذة هي وظيفة تساوي الصفر خارج بعض الفاصل الزمني المحدد (نافذة).

تقدير التباين $$$s ^ 2 (l)$ يعتمد على المعلمة $$$ل$ و منذ $$$ل$ يزيد وأكثر من 0 ، النتيجة $$$s ^ 2 (l)$ يبدأ في مراعاة الترابط التلقائي المحتمل في المخلفات $$$e_t$ .

وأخيرا ، فإن لاغرانج اختبار إحصاءات المضاعف $$$\ eta_ \ mu$ أو $$$\ eta_ \ tau$ يقارن مع القيم الحرجة. إذا تجاوزت إحصائيات اختبار لاجرانج المضاعف القيمة الحرجة المقابلة ، فإن الفرضية الفارغة $$$H_0 دولا$ (السلاسل الزمنية الثابتة) تنحرف لصالح فرضية بديلة $$$H_1$ (سلسلة زمنية غير ثابتة). خلاف ذلك ، لا يمكننا رفض فرضية فارغة $$$H_0 دولا$ حول المركزية من سلسلة زمنية.

القيم الحرجة غير مقاربة ، وبالتالي فهي أكثر ملاءمة لأحجام العينات الكبيرة. ومع ذلك ، في الممارسة العملية يتم استخدامها أيضا لعينة صغيرة. علاوة على ذلك ، القيم الحرجة مستقلة عن المعلمة $$$ل$ . ومع ذلك ، فإن إحصاءات اختبار مضاعف لاغرانج تعتمد على المعلمة $$$ل$ . لا يقدم مؤلفو اختبار KPSS أي خوارزمية عامة لاختيار المعلمة المناسبة. $$$ل$ . عادة ما يتم إجراء الاختبار من أجل $$$ل$ في حدود 0 إلى 8.

مع زيادة $$$ل$ نحن أقل عرضة لرفض الفرضية الفارغة $$$H_0 دولا$ حول الثبات ، والذي يؤدي جزئيًا إلى انخفاض في قوة الاختبار ويمكن أن يعطي نتائج مختلطة. ومع ذلك ، بشكل عام ، يمكننا القول أنه إذا كانت الفرضية الفارغة $$$H_0 دولا$ لا يتم رفض المركزية في السلسلة الزمنية حتى في القيم الصغيرة $$$ل$ (0 ، 1 أو 2) ، نستنتج أن السلاسل الزمنية التي تم التحقق منها ثابتة.

مقارنة نتائج الاختبار

تم تطوير المنهجية التالية لتقييم احتمال التماثل.

1. يتم فحص جميع السلاسل الزمنية للتأكد من صحتها من الدرجة الأولى باستخدام اختبار ديكي فولر بمستوى دلالة قدره 0.05. فقط سلسلة متكاملة من الدرجة الأولى تعتبر أدناه.
2. تشتمل السلسلة القابلة للتكامل من الدرجة الأولى والتي تم الحصول عليها في المادة 1 على أزواج من خلال الجمع دون تكرار.
3. يتم اختبار أزواج الأسهم الموضوعة في الفقرة 2 من أجل التكامل المشترك باستخدام اختبار Angle-Granger. نتيجة لذلك ، يتم تحديد الأزواج المختلطة.
4. يتم اختبار بقايا الانحدار التي تم الحصول عليها نتيجة للاختبار في الفقرة 3 للتأكد من ثباتها باستخدام اختبار KPSS. وبالتالي ، يتم الجمع بين نتائج الاختبارين.
5. يتم تبادل السلاسل الزمنية في الأزواج المدمجة المدمجة من البند 2 والتحقق مرة أخرى من أجل التكامل المشترك باستخدام اختبار Angle-Granger ، وهذا هو ، ونحن نفحص ما إذا كانت العلاقة بين السلاسل الزمنية متماثلة.
6. يتم تبادل السلاسل الزمنية في الأزواج المدمجة من البند 4 ويتم فحص بقايا الانحدار مرة أخرى للتأكد من ثباتها باستخدام اختبار KPSS ، أي أننا سنبحث فيما إذا كانت العلاقة بين السلاسل الزمنية متماثلة.

يتم تنفيذ جميع الحسابات باستخدام حزمة MATLAB. يتم عرض النتائج في الجدول أدناه. لكل اختبار ، لدينا عدد من العلاقات التي هي متناظرة وفقا لنتائج الاختبار (ملحوظ $$$S$ )؛ لدينا عدد من العلاقات غير المتماثلة وفقًا لنتائج الاختبار (ملحوظة) $$$¬S$ )؛ ولدينا احتمال تجريبي أن تكون النسبة متماثلة وفقًا لنتائج الاختبار ( $$$P (S) = \ frac {S} {S + ¬S}$ ).

في بورصة موسكو:


في بورصة نيويورك:

نتائج الاختبار الخلفي

دعونا نقارن نتائج استراتيجية التداول على البيانات التاريخية للأزواج المدمجة المدمجة المحددة باستخدام اختبار Angle-Granger وللأزواج المدمجة المدمجة المحددة باستخدام اختبار KPSS.

كما يتضح من الجدول ، نظرًا لتعريف أكثر دقة لأزواج الأسهم المدمجة ، فقد كان من الممكن زيادة متوسط ​​العائد السنوي عند تداول زوج متكامل مدمج بنسبة 9.21٪. وبالتالي ، يمكن أن تزيد المنهجية المقترحة من ربحية التداول الحسابي باستخدام استراتيجيات محايدة للسوق.

التفسير البديل

كما رأينا أعلاه ، فإن نتائج اختبار Angle-Granger هي يانصيب. بالنسبة للبعض ، سوف تبدو أفكاري قاطعة بشكل مفرط ، لكنني أعتقد أنه من المنطقي ألا نأخذ الفرضية الفارغة ، التي أكدها التحليل الإحصائي ، في الإيمان.

إن المحافظة على الطريقة العلمية لاختبار الفرضيات هو أنه عند تحليل البيانات ، يمكننا فقط التوصل إلى استنتاج صحيح واحد: يتم رفض الفرضية الفارغة عند مستوى الأهمية المحدد. هذا لا يعني أن البديل صحيح. $$$H_1$ - لقد تلقينا للتو أدلة غير مباشرة على مصداقيتها على أساس "دليل نموذجي من العكس". في حالة عندما يكون صحيحا $$$H_0 دولا$ ، يتم توجيه الباحث أيضًا إلى استنتاج حذر: استنادًا إلى البيانات التي تم الحصول عليها في الظروف التجريبية ، لم يكن من الممكن العثور على أدلة كافية لرفض الفرضية الفارغة.

في انسجام مع أفكاري في سبتمبر 2018 ، كتب مقال من قبل أصحاب النفوذ يحثون على التخلي عن مفهوم "الأهمية الإحصائية" ونموذج اختبار الفرضية الفارغة.

الأهم من ذلك: "اقتراحات مثل تغيير مستوى العتبة $$$ع$ - القيم الافتراضية ، أو استخدام فواصل الثقة مع التركيز على ما إذا كانت تحتوي على صفر أم لا ، أو استخدام معامل بايز إلى جانب التصنيفات المقبولة عالمياً لتقييم قوة الأدلة التي تأتي من كل المشاكل نفسها أو ما شابه الاستخدام الحالي $$$ع$ - القيم بمستوى 0.05 ... هي شكل من أشكال الخيمياء الإحصائية التي تعد بوعد خاطئ بتحويل العشوائية إلى موثوقية ، ما يسمى "غسل عدم اليقين" (Gelman، 2016) ، والذي يبدأ بالبيانات وينتهي باستنتاجات ثنائية حول الحقيقة أو الزيف - بيانات ثنائية أن "هناك تأثير" أو "لا يوجد تأثير" - على أساس تحقيق بعض $$$ع$ القيم أو قيمة العتبة الأخرى.

(Carlin, 2016; Gelman, 2016), , ( ) , , .»

النتائج

لقد رأينا أنه على الرغم من أن خاصية التناظر في علاقة التكامل المشترك يجب أن تكون مقتنعة نظريًا ، إلا أن البيانات التجريبية تختلف عن الحسابات النظرية. أحد التفسيرات لهذا التناقض هو القوة المنخفضة لاختبار ديكي فولر.

كمنهجية جديدة لتحديد أزواج الأصول المدمجة ، تم اقتراح اختبار بقايا الانحدار التي تم الحصول عليها باستخدام اختبار Angle-Granger للتأكد من عدم ثباتها باستخدام اختبار KPSS والجمع بين نتائج هذه الاختبارات ؛ ودمج نتائج اختبار Angle-Granger واختبار KPSS لكل من الانحدار المباشر والعكس.

أجريت الاختبارات الخلفية على بيانات بورصة موسكو لعام 2017. وفقًا لنتائج الاختبارات الخلفية ، فإن متوسط ​​العائد السنوي عند استخدام المنهجية لتحديد أزواج الأسهم المختلطة المذكورة أعلاه كان 22.72٪. وبالتالي ، بالمقارنة مع تحديد أزواج الأسهم المدمجة باستخدام اختبار Angle-Granger ، كان من الممكن زيادة متوسط ​​العائد السنوي بنسبة 9.21 ٪.

التفسير البديل للمفارقة هو عدم اتخاذ الفرضية الفارغة ، التي أكدها التحليل الإحصائي ، عن الإيمان. النموذج الخالي للفرضية واختبار الانقسام الذي يقدمه مثل هذا النموذج يمنحنا شعورًا خاطئًا بمعرفة السوق.

عندما بدأت للتو بحثي ، بدا لي أنه يمكنك أن تأخذ السوق وتضعه في "مفرمة اللحم" الخاصة بالاختبارات الإحصائية وتحصل على صفوف لذيذة عند الخروج. للأسف ، الآن أرى أن مفهوم القوة الغاشمة الإحصائية لن ينجح.

سواء كان هناك تعاون مشترك في السوق أم لا - بالنسبة لي ، يبقى هذا السؤال مفتوحًا. لا يزال لديّ أسئلة كبيرة لمؤسسي هذه النظرية. اعتدت أن أشعر ببعض الخوف في الغرب وأولئك العلماء الذين طوروا الرياضيات المالية في وقت كانت فيه الاقتصاد القياسي تعتبر برجوازية فاسدة في الاتحاد السوفيتي. يبدو لي أننا كنا متخلفين للغاية ، وفي مكان ما في أوروبا وأمريكا ، كانت آلهة التمويل جالسة ، الذين كانوا يعرفون الكرامة المقدسة للحقيقة.

الآن أفهم أن العلماء الأوروبيين والأمريكيين لا يختلفون كثيرًا عن عالمنا ، والفرق الوحيد هو في حجم الدجال. يجلس علماءنا في قلعة عاج ، ويكتبون بعض الهراء ويحصلون على منح بمبلغ 500 ألف روبل. في الغرب ، يجلس العلماء أنفسهم حول نفس قلعة العاج ، ويكتبون عن نفس الهراء ويحصلون على "نوبل" ومنح بقيمة 500 ألف دولار لهذا الغرض. هذا هو الفرق كله.

في الوقت الحالي ، ليس لدي رؤية واضحة لموضوع بحثي. من الخطأ القول أن "جميع صناديق التحوط تستخدم تداول الزوج" لأن معظم صناديق التحوط تفلس بنفس القدر.

لسوء الحظ ، عليك دائمًا التفكير واتخاذ القرارات برأسك ، خاصةً عندما نخاطر بالمال.