تتمتع البرمجة الديناميكية بسمعة جيدة للطريقة التي تدرس بها في الجامعة ، ثم تذكرها فقط أثناء المقابلات. ولكن في الواقع ، فإن الطريقة قابلة للتطبيق في العديد من الحالات. في الواقع ، هذه تقنية لحل المشكلات بفعالية ويمكن تقسيمها إلى العديد من المهام الفرعية المتكررة للغاية .

في المقالة سأعرض تطبيقًا حقيقيًا مثيرًا للاهتمام للبرمجة الديناميكية - مهمة نحت التماس. تم توضيح المهمة والمنهجية بالتفصيل في عمل Avidan و Shamir "قطع طبقات لتغيير حجم الصور على أساس المحتوى" (مقالة في المجال العام).

هذه هي واحدة من سلسلة من المقالات حول البرمجة الديناميكية. إذا كنت ترغب في تنظيف الطرق ، فراجع المقدمة المصوّرة للبرمجة الديناميكية .

تغيير حجم الصورة على أساس المحتوى

لحل مشكلة حقيقية باستخدام البرمجة الديناميكية ، تحتاج إلى صياغتها بشكل صحيح. يصف هذا القسم الإعدادات المسبقة اللازمة للمهمة المحددة.

يصف مؤلفو المقالة الأصلية تغيير حجم الصورة الموجهة للمحتوى ، أي تغيير عرض أو ارتفاع الصورة بناءً على المحتوى. انظر العمل الأصلي للحصول على التفاصيل ، وأنا أقدم لمحة موجزة. افترض أنك تريد تغيير حجم صورة متصفحي:


منظر علوي لمتصفحي وسط المحيط الهادئ ، مع وجود موجات مضطربة على اليمين. الصورة: كيريل دوبريف على بيكسباي

كما هو موضح بالتفصيل في المقالة ، هناك عدة طرق لتقليل عرض الصورة: هذه هي عمليات قص وتقطيع قياسية ، مع عيوبها الكامنة ، بالإضافة إلى إزالة أعمدة البكسل من الوسط. كما يمكنك أن تتخيل ، يترك هذا التماس مرئيًا في الصورة ، حيث لا تتطابق الصورة على اليمين واليسار. وبهذه الطريقة ، يمكنك حذف كمية محدودة فقط من الصور.


محاولة لتقليل العرض من خلال تقليم الجانب الأيسر وتقليص الكتلة من الوسط. هذا الأخير يترك التماس مرئية.

يصف أفيدان وشامير في المقالة الأسلوب الجديد "نحت التماس". يحدد أولاً مناطق "الطاقة المنخفضة" الأقل أهمية ، ثم يحسب "طبقات" الطاقة المنخفضة التي تمر عبر الصورة. في حالة تقليل عرض الصورة ، يتم تحديد التماس العمودي من أعلى الصورة إلى الأسفل ، والذي يتم نقله في كل سطر إلى اليسار أو اليمين بما لا يزيد عن بكسل واحد.

في صورة سيرفر ، يمر أدنى التماس للطاقة عبر منتصف الصورة ، حيث يكون الماء أهدأ. هذا يتفق مع الحدس لدينا.


يظهر التماس ذو الطاقة المنخفضة الموجود في صورة الراكب بخط أحمر يبلغ عرضه 5 بكسل للرؤية ، على الرغم من أن التماس يبلغ عرضه بكسل واحد فقط.

بعد تحديد التماس بأقل طاقة ، ثم إزالته ، نقوم بتقليل عرض الصورة بمقدار بكسل واحد. تكرار هذه العملية مرارًا وتكرارًا يقلل بشكل كبير من عرض الصورة بأكملها.


سيرفر الصورة بعد تخفيض العرض بمقدار 1024 بكسل

مرة أخرى ، قامت الخوارزمية بإزالة المياه الساكنة في الوسط ، وكذلك على الجانب الأيسر من الصورة. ولكن على عكس المحاصيل ، يتم الحفاظ على نسيج الماء على اليسار ولا توجد انتقالات حادة. صحيح ، يمكنك أن تجد بعض التحولات غير الكاملة في الوسط ، ولكن النتيجة تبدو طبيعية بشكل أساسي.

تعريف طاقة الصورة

السحر هو العثور على أدنى التماس الطاقة. للقيام بذلك ، نقوم أولاً بتخصيص الطاقة لكل بكسل في الصورة. ثم نستخدم البرمجة الديناميكية للعثور على المسار من خلال الصورة بأقل طاقة - ستتم مناقشة هذه الخوارزمية بالتفصيل في القسم التالي. أولاً ، لنلقِ نظرة على كيفية تعيين قيم طاقة البكسل.

تتناول المقالة العلمية العديد من وظائف الطاقة واختلافاتها. لنقم بتعقيدها وأخذ وظيفة تلتقط ببساطة مقدار تغير اللون حول كل بكسل. لإكمال الصورة ، سوف أصف وظيفة الطاقة بمزيد من التفصيل في حال كنت تريد تنفيذها بنفسك ، ولكن هذا مجرد إعداد مسبق للحسابات البرمجية الديناميكية اللاحقة.


على اليسار هناك ثلاثة بكسلات من الظلام إلى النور. الفرق بين الأول والأخير عظيم. ثلاثة بكسلات داكنة على اليمين مع اختلاف بسيط في كثافة اللون

لحساب طاقة بكسل معين ، انظر إلى وحدات البكسل الموجودة على يسارها ويمينها. من ناحية المكون ، نقوم بحساب مربع المسافة بينهما ، أي مربع الفرق بين المكونات الحمراء والخضراء والزرقاء ، ثم نضيفها. نحن نفعل الشيء نفسه بالنسبة للبيكسلات أعلى وتحت الوسط. أخيرًا ، أضف المسافات الأفقية والرأسية.

$$

$$| \ Delta x | ^ 2 = (\ Delta r_x) ^ 2 + (\ Delta g_x) ^ 2 + (\ Delta b_x) ^ 2$$

$$

$$| \ Delta y | ^ 2 = (\ Delta r_y) ^ 2 + (\ Delta g_y) ^ 2 + (\ Delta b_y) ^ 2$$

$$

$$e (x، y) = | \ دلتا x | ^ 2 + | \ دلتا ذ ^ 2 دولا$$

التحذير الوحيد - على سبيل المثال ، إذا كان البيكسل على الحافة اليسرى ، فلا يوجد جار على اليسار. في هذه الحالة ، نقارن فقط مع بكسل الصحيح. يتم إجراء اختبارات مماثلة للبكسلات في الحواف العلوية واليمنى والسفلية.

تكون وظيفة الطاقة رائعة إذا كانت وحدات البكسل المجاورة مختلفة تمامًا في اللون ، وصغيرة إذا كانت متشابهة.


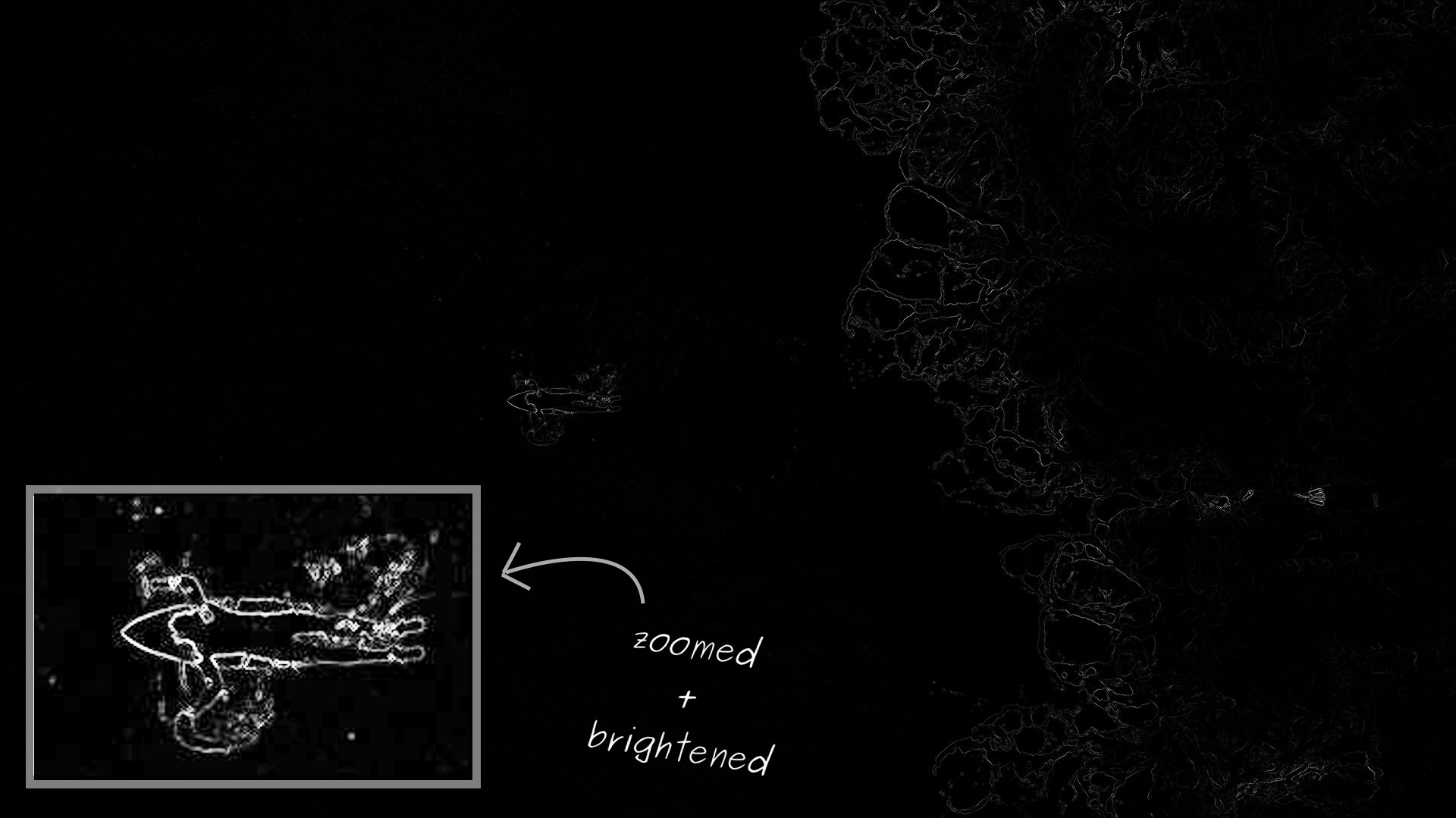طاقة كل بكسل في صورة سيرفر: أخف وزنا - كلما كان ذلك أعلى. كما هو متوقع ، فإن سيرفر لديه أعلى طاقة في الأمواج الوسطى والاضطرابات على اليمين

وظيفة الطاقة تعمل بشكل جيد على صورة سيرفر. ومع ذلك ، فإنه يأخذ مجموعة واسعة جدا من القيم. لذلك ، عند التقديم ، يبدو أنه في معظم الصور ، يكون للبكسلات طاقة صفرية. في الواقع ، هناك ببساطة قيم منخفضة للغاية مقارنة بالمناطق ذات الطاقة الأعلى. لتبسيط التصور ، قمت بتكبير العرض وأبرز هذه المنطقة.

ابحث عن طبقات منخفضة الطاقة مع برمجة ديناميكية

من خلال حساب طاقة كل بكسل ، يمكننا أن نجد التماس مع أدنى طاقة من أعلى الصورة إلى أسفل. ينطبق نفس التحليل على اللحامات الأفقية لتقليل ارتفاع الصورة الأصلية. ومع ذلك ، سوف نركز على تلك العمودية.

لنبدأ بالتعريف:

• التماس عبارة عن سلسلة من البكسل ، بكسل واحد في كل سطر. الشرط هو أن بين خطين متتاليين التنسيق $$$x$يتغير بنسبة لا تزيد عن بكسل واحد. هذا يحافظ على تسلسل التماس.
  
• التماس الذي يحتوي على أقل طاقة هو الذي يتم تقليل إجمالي طاقته على جميع وحدات البكسل في التماس.

من المهم أن نلاحظ أن المفصل مع أدنى طاقة لا يمر بالضرورة بكل البيكسلات ذات الطاقة الأقل. يتم أخذ الطاقة الإجمالية للجميع ، وليس وحدات البكسل الفردية ، في الاعتبار.


النهج الجشع لا يعمل. عند اختيار بكسل منخفض الطاقة في مرحلة مبكرة ، فإننا نتعثر في المنطقة عالية الطاقة في الصورة (المسار الأحمر إلى اليمين)

كما ترون ، لا يمكنك فقط اختيار أقل طاقة بكسل في السطر التالي.

نحن تقسيم المشكلة إلى مهام فرعية

المشكلة في النهج الجشع هي أنه عند اتخاذ قرار بشأن الخطوة التالية ، فإننا لا نأخذ في الاعتبار بقية التماس إلى الأمام. لا يمكننا النظر إلى المستقبل ، لكننا قادرون على مراعاة كل ما نعرفه الآن حتى الآن.

دعنا نقلب المهمة رأسًا على عقب. بدلاً من الاختيار بين عدة وحدات بكسل لمواصلة التماس واحد ، سنختار بين عدة طبقات للانتقال إلى بكسل واحد . ما نحتاج إلى فعله هو أخذ كل بكسل واختيار بين البكسلات الموجودة في السطر أعلاه ، والتي يمكن أن يأتي التماس منها. إذا قام كل بكسل في السطر أعلاه بترميز المسار الذي تم الانتقال إليه إلى هذه النقطة ، فنحن نتطلع بشكل أساسي إلى السجل الكامل لهذه النقطة.


لكل بكسل ، ندرس ثلاثة بكسلات في السطر أعلاه. خيار أساسي - أي من طبقات لمواصلة؟

يفترض هذا مهمة فرعية لكل بكسل في الصورة. يجب أن تجد المهمة الفرعية أفضل مسار لبكسل معين ، لذلك من الجيد ربط كل بكسل طاقة التماس منخفض الطاقة الذي ينتهي بهذا البيكسل .

على عكس النهج الجشع ، فإن النهج أعلاه يحاول بشكل أساسي جميع المسارات الممكنة من خلال الصورة. إنه فقط عند فحص جميع المسارات الممكنة ، يتم حل نفس المهام الفرعية مرارًا وتكرارًا ، مما يجعل هذا النهج خيارًا مثاليًا للبرمجة الديناميكية.

تعريف علاقة التكرار

كالعادة ، نحن الآن بحاجة إلى إضفاء الطابع الرسمي على الفكرة في علاقة تكرارية. هناك مهمة فرعية تقابل كل بكسل في الصورة الأصلية ، وبالتالي فإن المدخلات لعلاقة التكرار لدينا يمكن أن تكون مجرد إحداثيات $$$x$و $$$ذ$من هذا بكسل. يوفر هذا مدخلات عددًا صحيحًا ، مما يجعل من السهل تنظيم المهام الفرعية ، فضلاً عن القدرة على تخزين القيم المحسوبة مسبقًا في صفيف ثنائي الأبعاد.

تحديد وظيفة $$$M (x، y)$والذي يمثل طاقة التماس العمودي بأقل طاقة. يبدأ في الجزء العلوي من الصورة وينتهي بالبكسل $$$(س ، ذ)$. اسم $$$M$تم اختيارها كما في المقالة العلمية الأصلية.

أولاً ، تحتاج إلى إصدار أساسي. يبلغ طول كل الطبقات التي تنتهي في السطر العلوي بكسلًا واحدًا فقط. وبالتالي ، التماس مع الحد الأدنى من الطاقة هو مجرد بكسل مع الحد الأدنى من الطاقة:

$$

$$M (x، 0) = e (x، 0)$$

بالنسبة للبكسل في الصفوف المتبقية ، انظر إلى البكسل في الأعلى. نظرًا لأن التماس يجب أن يكون مستمرًا ، فنحن نأخذ في الاعتبار ثلاثة بكسلات فقط موجودة في أعلى اليسار وأعلى وأعلى اليمين. من بينهم نختار التماس مع أقل طاقة ، والتي تنتهي في واحدة من هذه بكسل ، وإضافة طاقة بكسل الحالية:

$$

$$M (x، y) = e (x، y) + \ min \ تبدأ {cases} M (x - 1، y - 1) \\ M (x، y - 1) \\ M (x + 1، y - 1) \ end {cases}$$

كموقف حدودي ، فكر في الحالة عندما يكون البيكسل الحالي في الحافة اليسرى أو اليمنى من الصورة. في هذه الحالات ، نتجاهل $$$M (x-1 ، y-1)$بكسل على الحافة اليسرى أو $$$M (x + 1 ، y-1)$على الحافة اليمنى.

أخيرًا ، تحتاج إلى استخراج طاقة التماس ذي الطاقة المنخفضة ، والتي تغطي ارتفاع الصورة بالكامل. هذا يعني أننا ننظر إلى الخط السفلي للصورة وتحديد التماس الطاقة المنخفضة التي تنتهي في واحدة من هذه بكسل. للصور واسعة $$$W$و طويل القامة $$$H$بكسل:

$$

$$\ min_ {0 \ le x <W} M (x، H - 1)$$

لذلك ، حصلنا على علاقة تكرار مع جميع الخصائص الضرورية:

• علاقة التكرار لها مدخلات عدد صحيح.
  
• الجواب النهائي سهل الاستخلاص من العلاقة.
  
• النسبة تعتمد على الذات.

التحقق من المهام الفرعية DAG (الرسم البياني الحاد المنحى)

منذ كل مهمة فرعية $$$M (x، y)$يتوافق مع بكسل واحد من الصورة الأصلية ، والرسم البياني التبعية من السهل جدا تصور. فقط ضعهم على شبكة ثنائية الأبعاد ، كما في الصورة الأصلية!


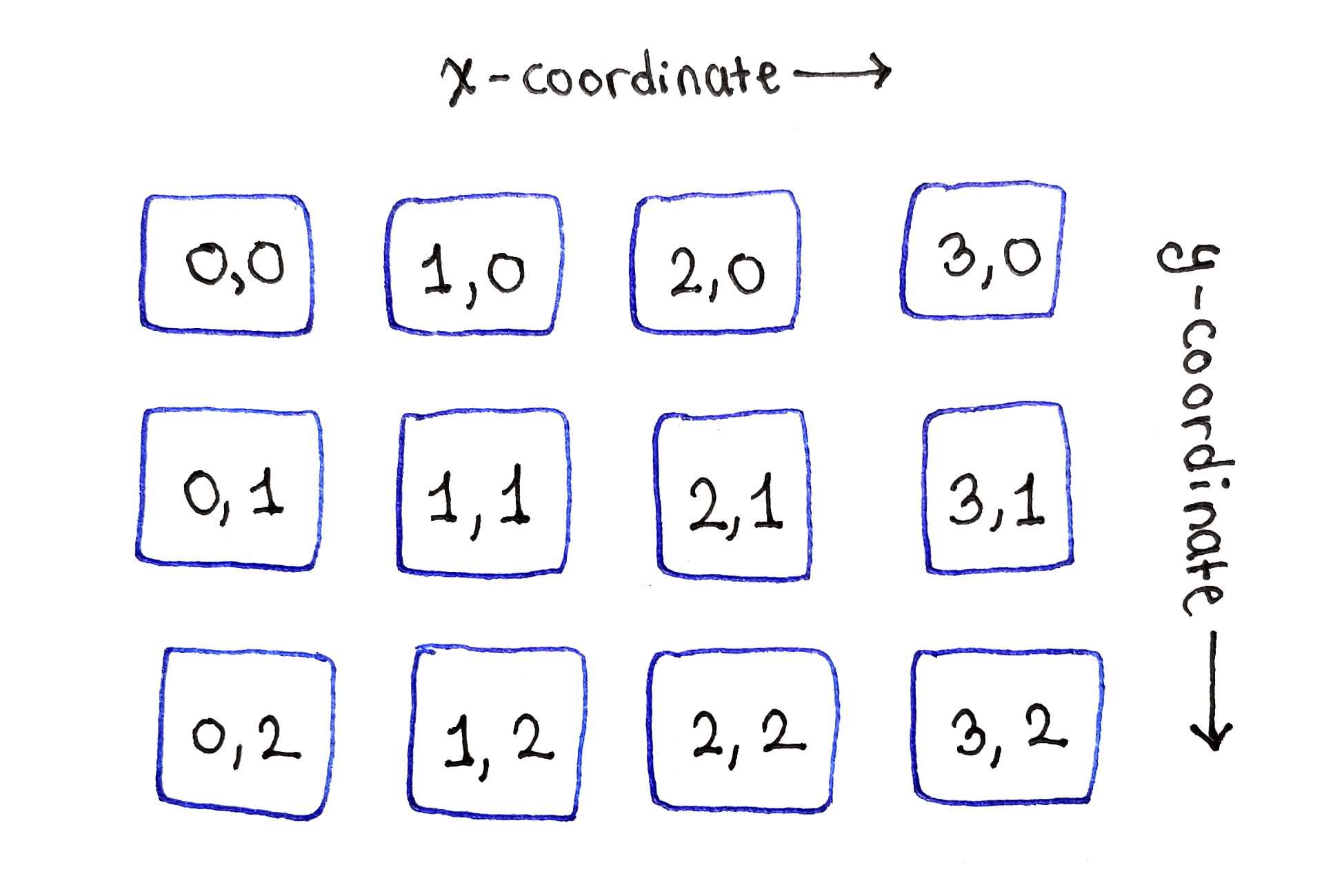تقع المهام الفرعية في شبكة ثنائية الأبعاد ، مثل وحدات البكسل في الصورة الأصلية

كما يلي من السيناريو الأساسي لعلاقة التكرار ، يمكن تهيئة السطر العلوي من المهام الفرعية بقيم الطاقة لوحدات البكسل الفردية.


الصف العلوي مستقل عن المهام الفرعية الأخرى. لاحظ عدم وجود أسهم من الصف العلوي من الخلايا

في السطر الثاني ، تبدأ التبعيات في الظهور. أولاً ، في أقصى اليسار في الصف الثاني ، نواجه وضع حدودي. لأنه لا توجد خلايا على اليسار ، الخلية $$$(1،0)$يعتمد فقط على الخلايا الموجودة فوقه مباشرة وعلى الجزء العلوي الأيمن. سيحدث الشيء نفسه لاحقًا مع الخلية الموجودة في أقصى اليسار في الصف الثالث.


تعتمد المهام الفرعية الموجودة على الحافة اليسرى على مهمتين فرعيتين فقط فوقها

في الخلية الثانية من الصف الثاني (1،1) ، نرى المظهر الأكثر شيوعا لعلاقة التكرار. تعتمد هذه الخلية على ثلاث خلايا: أعلى اليسار ، أعلى اليمين وأعلى اليمين. تنطبق بنية التبعية هذه على جميع الخلايا "المتوسطة" في الصفوف الثانية واللاحقة.


تعتمد المهام الفرعية بين الحواف اليمنى واليسرى على المهام الفرعية الثلاثة في الأعلى

أخيرًا ، تمثل الخلية الموجودة على الحافة اليمنى الموقف الحدودي الثاني. نظرًا لعدم وجود المزيد من الخلايا على اليمين ، فإن ذلك يعتمد فقط على الخلايا الموجودة في أعلى الصفحة وعلى أعلى اليسار.


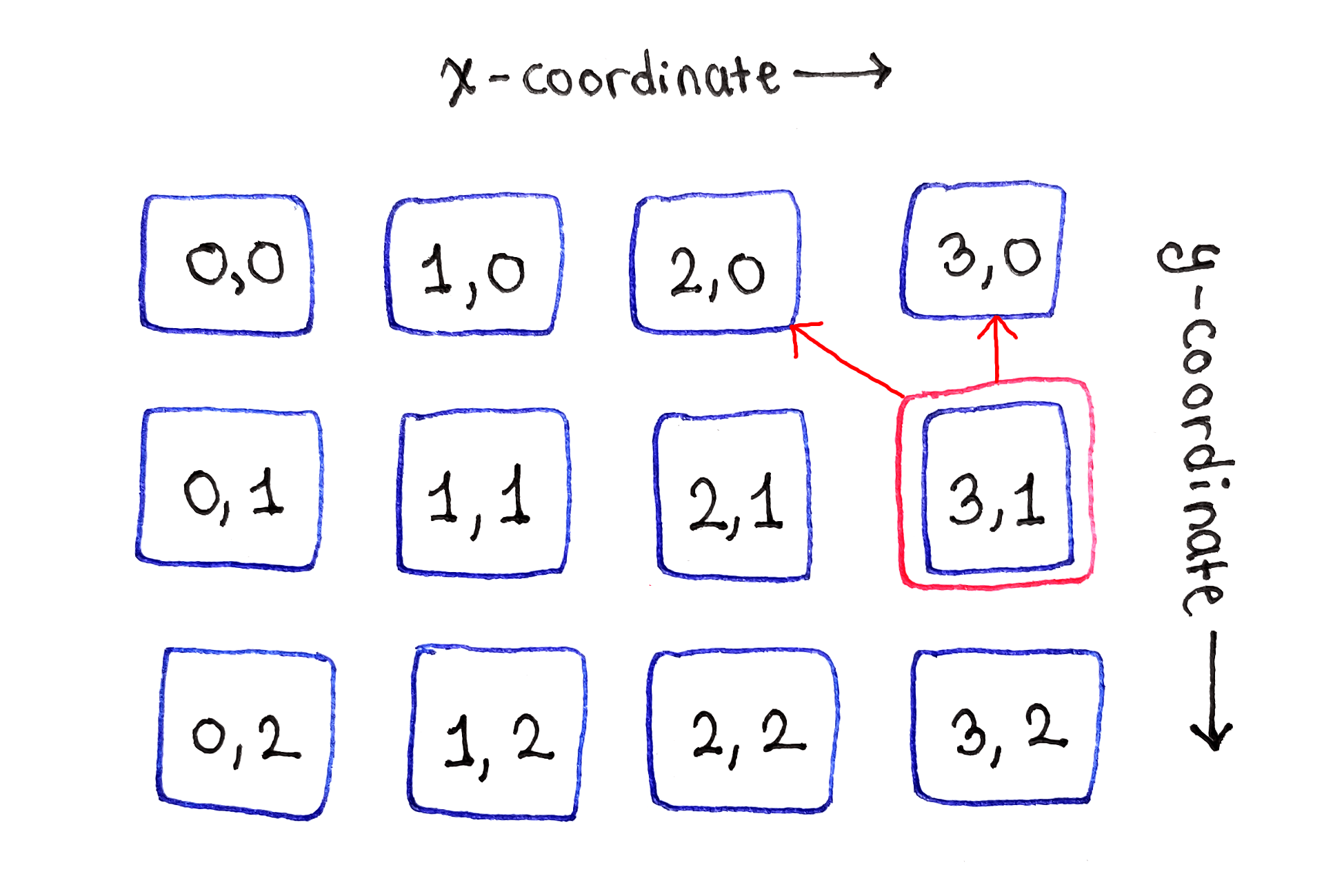تعتمد المهام الفرعية على الحافة اليمنى على خليتين فقط في الأعلى

يتم تكرار العملية لجميع الخطوط اللاحقة.


نظرًا لوجود العديد من الأسهم في الرسم البياني التبعية ، تعرض هذه الرسوم المتحركة التبعيات لكل مهمة فرعية بدورها

يخيفك الرسم البياني التبعية الكامل بعدد كبير من الأسهم ، ولكن النظر إليه واحدًا تلو الآخر يساعد في إنشاء أنماط واضحة.

تنفيذ من أسفل إلى أعلى

بعد إجراء هذا التحليل ، حصلنا على أمر المعالجة:

• انتقل من أعلى الصورة إلى الأسفل.
  
• كل سطر يمكن أن تعمل في أي ترتيب. الخيار الطبيعي هو الانتقال من اليسار إلى اليمين.

نظرًا لأن كل صف يعتمد فقط على الصف السابق ، تحتاج إلى حفظ صفين فقط من البيانات: صف للصف السابق وواحد للصف الحالي. بالانتقال من اليسار إلى اليمين ، يمكننا حتى تجاهل العناصر الفردية من الصف السابق عند استخدامها. ومع ذلك ، يؤدي هذا إلى تعقيد الخوارزمية ، حيث سيتعين عليها معرفة أي أجزاء من السطر السابق يمكن التخلص منها.

في شفرة Python التالية ، يكون الإدخال عبارة عن قائمة من الخطوط ، حيث يحتوي كل سطر على قائمة بالأرقام التي تمثل طاقات البكسل الفردية في هذا السطر. يسمى الإدخال pixel_energies ، pixel_energies[y][x] طاقة البكسل في الإحداثيات $$$(س ، ذ)$.

لنبدأ بحساب طاقة طبقات الصف العلوي ، ببساطة عن طريق نسخ طاقات البكسل الفردية في الصف العلوي:

 previous_seam_energies_row = list(pixel_energies[0]) 

ثم ننتقل عبر خطوط الإدخال المتبقية ، ونحسب طاقات التماس لكل سطر. الجزء الأكثر "صعوبة" هو تحديد عناصر السطر السابق للإشارة إليها ، حيث لا توجد وحدات بكسل على يسار الحافة اليسرى أو إلى يمين الحافة اليمنى.

عند كل تكرار ، يتم إنشاء قائمة جديدة بطاقات التماس للخط الحالي. في نهاية التكرار ، نستبدل بيانات السطر السابق ببيانات السطر الحالي للتكرار التالي. هذه هي الطريقة التي نتجاهل بها السطر السابق:

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row 

نتيجة لذلك ، previous_seam_energies_row يحتوي على طاقة التماس للخط السفلي. نجد الحد الأدنى للقيمة في هذه القائمة - وهذه هي الإجابة!

 min(seam_energy for seam_energy in previous_seam_energies_row) 

يمكنك اختبار هذا التطبيق من خلال التفاف التعليمة البرمجية في دالة ، ثم استدعاءها باستخدام صفيف ثنائي الأبعاد الذي قمت بإنشائه. تم اختيار المدخلات التالية بحيث يفشل النهج الجشع ، مع وجود تماس واضح بأقل طاقة:

 ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES)) 

التعقيد المكاني والزماني

يتوافق كل بكسل في الصورة الأصلية مع مهمة فرعية واحدة. بالنسبة لكل مهمة من المهام الفرعية ، لا يوجد أكثر من ثلاث تبعيات ، لذا فإن حل كل منها ينطوي على قدر ثابت من العمل. يقام الصف الأخير مرتين. لذلك لصورة واسعة $$$W$و طويل القامة $$$H$بكسل تعقيد الوقت $$$O (W × H + W)$.

في كل لحظة من الوقت ، لدينا قائمتان: واحدة للسطر السابق وأخرى للتيار. في الأول $$$W$العناصر ، والثاني يزيد تدريجيا ل $$$W$. وبالتالي ، فإن التعقيد المكاني يساوي $$$O (2W)$هذا عادل $$$O (w)$.

لاحظ أننا إذا تجاهلنا بالفعل عناصر بيانات الصف السابق ، فسنقصّر قائمة عناصر الصف السابق بنفس السرعة التي تنمو بها قائمة الصف الحالي. وهكذا سيبقى التعقيد المكاني $$$O (w)$. على الرغم من أن العرض قد يختلف ، إلا أن هذا ليس مهمًا في العادة.

انخفاض مؤشرات الطاقة إلى الوراء

لذلك ، وجدنا معنى التماس الطاقة المنخفضة ، ولكن ماذا تفعل مع هذه المعلومات؟ بعد كل شيء ، في الواقع ، نحن لسنا قلقين بشأن أهمية الطاقة ، ولكن التماس نفسه! المشكلة هي أنه لا توجد طريقة من البيكسل النهائي للعودة إلى بقية التماس.

هذا هو ما فاتني في المقالات السابقة ، ولكن نفس الشيء ينطبق على العديد من مشكلات البرمجة الديناميكية. على سبيل المثال ، إذا كنت تتذكر مهمة السارق المنزلي ، فقد وجدنا الحد الأقصى لقيمة السرقة ، ولكن ليس المنازل المحددة التي يجب سرقتها للحصول على هذا المبلغ.

تمثيل مؤشرات الظهر

الجواب العام: تخزين مؤشرات الظهر . في مهمة قطع اللحامات ، لا نحتاج فقط إلى قيمة طاقة التماس عند كل بكسل. تحتاج أيضًا إلى معرفة أي من وحدات البكسل في الصف السابق أدت إلى هذه الطاقة. من خلال تخزين هذه المعلومات ، يمكننا اتباع المؤشرات العكسية مباشرة حتى السطر العلوي ، والحصول على إحداثيات جميع البيكسلات التي تشكل المفصل بأقل طاقة.

أولاً ، قم بإنشاء فصل لتخزين الطاقة ومؤشرات الخلفية. سيتم استخدام الطاقة لحساب المهام الفرعية. نظرًا لأن المؤشر الخلفي يحدد البيكسل في السطر السابق الذي أعطى الطاقة الحالية ، يمكننا أن نتخيل ذلك بمجرد تنسيق x.

 class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row 

لن تكون نتيجة الحساب لكل مهمة فرعية مجرد رقم ، بل ستكون نسخة من هذه الفئة.

تخزين مؤشر إلى الوراء

في النهاية ، تحتاج إلى العودة على طول ارتفاع الصورة بالكامل ، باتباع العلامات العكسية لاستعادة التماس بأقل طاقة. لسوء الحظ ، هذا يعني أنك تحتاج إلى تخزين مؤشرات لجميع وحدات البكسل في الصورة ، وليس فقط في السطر السابق.

للقيام بذلك ، نقوم ببساطة بحفظ النتيجة الكاملة لجميع المهام الفرعية ، على الرغم من أنه من الممكن تقنيًا رفض الطاقات العددية للتماس الخطوط السابقة. يتم تخزين النتائج في صفيف ثنائي الأبعاد ، والذي يشبه صفيف الإدخال.

لنبدأ بالسطر الأول ، الذي يحتوي على طاقات بكسل فردية فقط. نظرًا لعدم وجود خط سابق ، فإن جميع مؤشرات الخلفية مفقودة ، ولكن للتناسق ، سنظل نُخزن مثيلات SeamEnergyWithBackPointers :

 seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ]) 

تعمل الحلقة الرئيسية بشكل أساسي مع التنفيذ السابق ، مع وجود الاختلافات التالية:

• تحتوي بيانات الصف السابق على مثيلات SeamEnergyWithBackPointer ، لذلك ، عند حساب قيمة نسبة التكرار ، يجب أن تبحث عن طاقة التماس داخل هذه الكائنات.
  
• حفظ البيانات للبكسل الحالي ، تحتاج إلى إنشاء مثيل جديد من SeamEnergyWithBackPointer . سنقوم هنا بتخزين طاقة التماس للبكسل الحالي ، وكذلك إحداثي x من السطر السابق ، المستخدم لحساب طاقة التماس الحالية.
  
• في نهاية كل صف ، بدلاً من تجاهل بيانات الصف السابق ، نضيف ببساطة بيانات الصف الحالي إلى seam_energies .

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row) 

اتبع العلامات

الآن يتم ملء جدول المهام الفرعية بالكامل ويمكننا استعادة التماس بأقل طاقة. نبدأ بالبحث عن إحداثي x في الخلاصة ، والذي يتوافق مع المفصل بأقل طاقة:

 # Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy ) 

انتقل الآن من أسفل الصورة إلى الأعلى ، وتغيير $$$ذ$من len(seam_energies) - 1 إلى صفر. في كل تكرار ، أضف الزوج الحالي $$$(س ، ذ)$إلى القائمة التي تمثل التماس لدينا ، ثم قم بتعيين القيمة $$$x$للكائن الذي يشير إليه SeamEnergyWithBackPointer في الصف الحالي.

 # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse() 

لذا تم بناء التماس لأعلى ، ثم يمكن قراءة القائمة بترتيب عكسي ، إذا كنت بحاجة إلى إحداثيات من الأعلى إلى الأسفل.

التعقيد المكاني والزماني

يشبه التعقيد الزمني التعقيد الزمني ، لأننا ما زلنا بحاجة إلى معالجة كل بكسل مرة واحدة. بعد النظر إلى السطر الأخير والعثور على المفصل بأقل طاقة ، نرفع ارتفاع الصورة بالكامل لاستعادة المفصل. لذلك بالنسبة للصورة $$$W × H$تعقيد الوقت يساوي $$$O (W × H + W + H)$.

بالنسبة إلى وحدة التخزين ، ما زلنا نحتفظ بكمية ثابتة من البيانات لكل مهمة فرعية ، لكننا الآن لا نتجاهل أي بيانات. لذلك نحن نستخدم حجم $$$O (W × H)$.

إزالة التماس منخفضة الطاقة

بمجرد العثور على المفصل العمودي مع أدنى طاقة ، يمكننا ببساطة نسخ وحدات البكسل من الصورة الأصلية إلى صورة جديدة. يحتوي كل سطر من الصورة الجديدة على جميع البيكسلات من الخط المقابل للصورة الأصلية ، باستثناء البكسل من التماس مع أدنى طاقة. بما أننا نحذف بكسل واحد في كل صف ، نبدأ من الصورة $$$W × H$ثم نحصل على الصورة $$$(W - 1) × H$.

يمكننا تكرار هذه العملية عن طريق إعادة حساب وظيفة الطاقة في الصورة الجديدة وإيجاد التماس أدنى طاقة عليها. يبدو أنه من المغري إيجاد أكثر من تماس منخفض الطاقة في الصورة الأصلية ، ثم حذفها جميعًا مرة واحدة. المشكلة هي أن اثنين من طبقات يمكن أن تتقاطع. عند حذف الأول ، يصبح الثاني غير صالح لأن بكسل واحد أو أكثر مفقود منه.


الرسوم المتحركة لعملية إزالة التماس. من الأفضل مشاهدتها في وضع ملء الشاشة للحصول على رؤية أوضح للدرزات

كل إطار من الفيديو هو صورة في كل التكرار مع التصور المتراكب للتماس مع أقل طاقة.

مثال آخر

تحتوي المقالة على الكثير من التوضيحات المفصلة ، لذلك دعونا ننتهي بمجموعة من الصور الجميلة! تُظهر الصورة التالية تشكيلًا صخريًا في حديقة الأقواس الوطنية:


تشكيل الصخور مع وجود ثقب في حديقة الأقواس الوطنية. الصورة: مايك غواد على فليكر

وظيفة الطاقة لهذه الصورة:


طاقة كل بكسل في الصورة: أفتح - كلما ارتفعت. انتبه إلى الطاقة العالية حول حافة الثقب.

نتيجة الحساب ، يتم الحصول على مثل هذا التماس مع أدنى طاقة. لاحظ أنه يمر عبر الصخرة على اليمين ، ويدخل مباشرة في تكوين الصخور حيث يتطابق الجزء المضيء في الجزء العلوي من الصخور مع لون السماء. ربما يجب عليك اختيار وظيفة أفضل للطاقة!


يظهر التماس الأقل طاقة الموجود في الصورة بخط أحمر يبلغ عرضه 5 بكسل للرؤية ، على الرغم من أن التماس يبلغ عرضه بكسل واحد فقط.

أخيرًا ، صورة القوس بعد تغيير الحجم:


القوس بعد الضغط على 1024 بكسل

النتيجة بالتأكيد ليست مثالية: العديد من حواف الجبل من الصورة الأصلية مشوهة. قد يكون أحد التحسينات هو تنفيذ إحدى وظائف الطاقة الأخرى المدرجة في المقالة العلمية.

---

على الرغم من أن البرمجة الديناميكية تناقش عادةً من الناحية النظرية ، إلا أنها طريقة عملية مفيدة لحل المشكلات المعقدة. في هذه المقالة ، درسنا أحد تطبيقات البرمجة الديناميكية: تغيير حجم الصور لتناسب المحتوى عن طريق قطع اللحامات.

طبقنا نفس المبادئ الخاصة بتقسيم مهمة ما إلى مهام فرعية أصغر ، وتحليل التبعيات بين هذه المهام الفرعية ، ثم حل المهام الفرعية بترتيب يقلل من التعقيد المكاني والزمني للخوارزمية. بالإضافة إلى ذلك ، درسنا استخدام المؤشرات العكسية ليس فقط لإيجاد قيمة الطاقة للتماس الأمثل ، ولكن أيضًا لتحديد إحداثيات كل بكسل مكونة هذه القيمة. ثم طبقنا هذه الأجزاء على مشكلة حقيقية ، والتي تتطلب بعض المعالجة المسبقة وما بعد المعالجة للاستخدام الفعال حقًا لخوارزمية البرمجة الديناميكية.