🤾 🏮 🃏 نموذج رياضي لتلسكوب راديوي طويل المدى 🍦 👨 👎🏽

مقدمة

واحدة من أول التلسكوبات الراديوية التي بناها المغارة الأمريكية ريبر في عام 1937. كان التلسكوب الراديوي مرآة من الصفيح يبلغ قطره 9.5 متر مثبتة على إطار خشبي:

بحلول عام 1944 ، كان ريبر قد جمع أول خريطة لتوزيع موجات الراديو الفضائية في منطقة درب التبانة.

استلزم تطوير علم الفلك الراديوي عددًا من الاكتشافات: في عام 1946 ، تم اكتشاف انبعاث راديوي من كوكبة Cygnus ، وفي عام 1951 - الإشعاع خارج المجرة ، في عام 1963 - الكوازارات ، وفي عام 1965 ، تم تصوير إشعاع الخلفية بطول موجي 7.5 سم.

في عام 1963 ، تم بناء تلسكوب لاسلكي فريد بطول 300 متر في أريسيبو (بورتوريكو). هذا هو وعاء بلا حراك مع مشعع متحرك ، بنيت في شق طبيعي من التضاريس.

تتمتع التلسكوبات الراديوية الفردية بدقة زاوي صغيرة ، والتي تحددها الصيغة:

$\ Theta = \ frac {\ lambda} {d}$
حيث

$\ lambda$ - الطول الموجي

د

$د$ - قطر التلسكوب اللاسلكي.

من الواضح ، لتحسين الدقة ، من الضروري زيادة قطر الهوائي ، وهي مهمة صعبة جسديًا. كان من الممكن حلها مع ظهور تداخل الراديو.

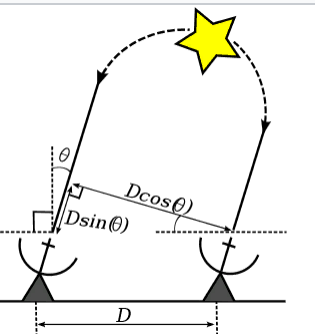
يمكن اعتبار مقدمة الموجة الكهرومغناطيسية المنبعثة من نجم بعيد بالقرب من الأرض مسطحة. في حالة أبسط مقياس تداخل ، يتكون من هوائيين ، يكون الفرق في مسار الأشعة التي تصل إلى هذين الهوائيين مساوياً لـ:

$\ Delta = D \ cdot sin (\ Theta)$ .
حيث:

د ل ت ا

$\ دلتا$ - الفرق في مسار الأشعة ؛

$D$ - المسافة بين الهوائيات ؛

$\ Theta$ - الزاوية بين اتجاه وصول الأشعة والعادي إلى الخط الذي توجد عليه الهوائيات.

في

$\ Theta = 0$ تتلخص الموجات التي تصل إلى كلا الهوائيات في المرحلة. في المرحلة المضادة ، ستظهر الموجات لأول مرة مع:

،

$\ Delta = \ frac {\ lambda} {2} ، \ Theta = arcsin \ frac {\ lambda} {2D}$ .
حيث:

$\ lambda$ - الطول الموجي.

سيكون الحد الأقصى التالي في

،

$\ Delta = \ lambda،$ الحد الأدنى في

$\ Delta = \ frac {3 \ lambda} {2}$ يتم الحصول على مخطط إشعاع متعدد البتلة (DN) ، وعرض الفص الرئيسي الذي في

$\ lambda << D$ يساوي

$\ lambda / D$ . يحدد عرض الفص الرئيسي الحد الأقصى للقرار الزاوي لمقياس التداخل الراديوي ، وهو يساوي تقريبًا عرض الفص.

التداخل الراديوي ذو القاعدة الطويلة جداً (VLBI) هو نوع من التداخل المستخدم في علم الفلك الراديوي حيث لا توجد عناصر الاستقبال في مقياس التداخل (التلسكوبات) على مقربة من المسافات القارية من بعضها البعض.

تسمح لك طريقة VLBI بدمج الملاحظات التي يتم إجراؤها بواسطة العديد من التلسكوبات ، وبالتالي محاكاة التلسكوب الذي تتساوى أبعاده مع المسافة القصوى بين التلسكوبات الأصلية. دقة الوضوح الزاوي لـ VLBI أكبر بعشرات الآلاف من المرات من دقة أفضل الأجهزة البصرية.

الوضع الحالي لشبكات VLBI

اليوم ، تستمع العديد من شبكات VLBI إلى الفضاء:

European –EVN (شبكة VLBI الأوروبية) ، التي تتألف من أكثر من 20 تلسكوبًا لاسلكيًا ؛
American -VLBA (صفيف خط الأساس طويل جدًا) ، والذي يتضمن عشرة مقاريب يبلغ قطر كل منها 25 مترًا ؛
اليابانية - تتكون JVN (شبكة VLBI اليابانية) من عشرة هوائيات موجودة في اليابان ، بما في ذلك أربعة هوائيات فلكية (مشروع VERA - استكشاف VLBI لقياس الفلك الراديوي) ؛
الأسترالية - LBA (خط الأساس الطويل) ؛
الصينية - CVN (شبكة VLBI الصينية) ، التي تتكون من أربعة هوائيات ؛
الكورية الجنوبية - KVN (شبكة VLBI الكورية) ، والتي تضم ثلاثة مناظير لاسلكية بطول 21 مترًا ؛
الروسية - استنادًا إلى مجمع التداخل الراديوي الدائم - "Kvazar-KVO" مع التلسكوبات الراديوية التي يبلغ قطرها 32 مترًا ، ومجهزة بمقاييس cryoradiadi حساسة للغاية في نطاق الطول الموجي من 1.35 سم إلى 21 سم ، ويبلغ طول القواعد - القطر الفعلي لـ "المرآة" المركبة - حوالي 4400 كم الشرق والغرب (انظر الصورة).

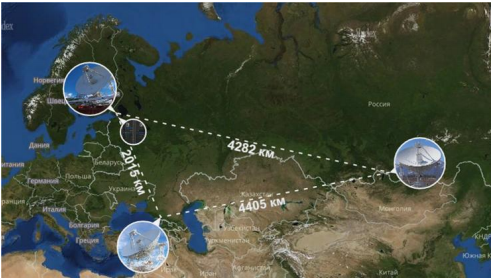
في مجمع VLBI "Kvazar-KVO" ، تُستخدم معايير الهيدروجين كمصدر تردد مرجعي لجميع تحويلات التردد ، والتي تستخدم الانتقال بين مستويات البنية الفائقة الدقة للحالة الأرضية لذرة الهيدروجين بتردد قدره 1420.405 MHz ، وهو ما يعادل 21 سم في علم الفلك الراديوي.

المهام حلها عن طريق VLBI

الفيزياء الفلكية. يتم إنشاء صور إذاعية لأجسام فضائية طبيعية (كوازارات وغيرها من الأجسام) بقرار من أعشار ومئات من الألماس (ميلي ثانية من قوس).
الدراسات الفلكية. بناء نظم تنسيق الوقت. أهداف البحث هي مصادر إذاعية ذات أحجام زاويّة صغيرة للغاية ، بما في ذلك مصادر الراديو شبه النوى ونواة المجرات الراديوية ، والتي ، نظرًا لبعدها الكبير ، تعد كائنات مثالية تقريبًا لإنشاء شبكة من الأجسام الثابتة الداعمة.
البحث في الميكانيكا السماوية وديناميات النظام الشمسي ، الملاحة الفضائية. يتيح تثبيت منارة على أسطح الكواكب وتتبع إشارات المحطات الأوتوماتيكية بين الكواكب استخدام طريقة VLBI لدراسة معلمات مثل الحركة المدارية للكوكب واتجاه محاور الدوران وتقدّمها وديناميات نظام الكوكب الساتلي. بالنسبة للقمر ، يتم أيضًا حل المشكلة المهمة جدًا المتمثلة في تحديد المعايرة الفيزيائية وتحديد ديناميات أنظمة القمر والأرض.

التنقل في الفضاء باستخدام VLBI

رصد تحركات رواد الفضاء على سطح القمر في عام 1971. انتقلوا بمساعدة روفر القمرية روفر. بلغت دقة تحديد موقعها بالنسبة للوحدة القمرية 20 سم وتعتمد بشكل رئيسي على اهتزاز القمر (Libration - ذبذبات دورية تشبه البندول بالنسبة إلى مركز كتلتها) ؛
دعم الملاحة لتسليم والتفريغ تحقيقات aerostat من المركبات الطائرة في جو فينوس (مشروع VEGA). تبلغ المسافة إلى كوكب الزهرة أكثر من 100 مليون كم ، وتبلغ طاقة الإرسال 1 وات فقط. تم إطلاق VEGA-1/2 في ديسمبر عام 1984. تم إسقاط البالونات في جو فينوس يومي 11 و 15 يونيو 1985. تم إجراء المراقبة لمدة 46 ساعة.

مخطط هيكلي لشبكة VLBI مبسطة

استنادًا إلى شبكة VLBI حقيقية ، باستخدام برنامج Python ، نقوم بتصميم نموذج VLBI مبسط في شكل نماذج منفصلة لكل وحدة أو عملية. هذه المجموعة من النماذج ستكون كافية لمراقبة العمليات الأساسية. يتم عرض الرسم البياني الهيكلي لشبكة VLBI المبسطة في الشكل:

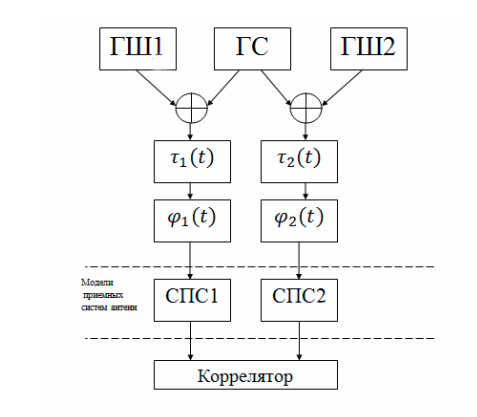
يتضمن النظام المكونات التالية:

مولد إشارة مفيدة المرحلة الطور (HS) ؛
مولدات الضوضاء (GSh1 ، GSh2). يحتوي النظام على اثنين من التلسكوبات الراديوية (هوائيات الاستقبال) التي لها ضوضاء خاصة بها. بالإضافة إلى ذلك ، هناك ضوضاء في الغلاف الجوي وغيرها من المصادر الطبيعية والاصطناعية للبث اللاسلكي ؛
وحدة تأخير زمني تحاكي تأخر زمني متفاوت خطيًا بسبب دوران الأرض ؛
المرحلة شيفتر محاكاة تأثير دوبلر.
نظام تحويل الإشارة (SPS) ، الذي يتكون من مذبذب محلي ، لنقل الإشارة إلى أسفل في التردد ، ومرشح تمرير النطاق ؛
متداول العملات الأجنبية.

تظهر دائرة الارتباط في الشكل التالي:

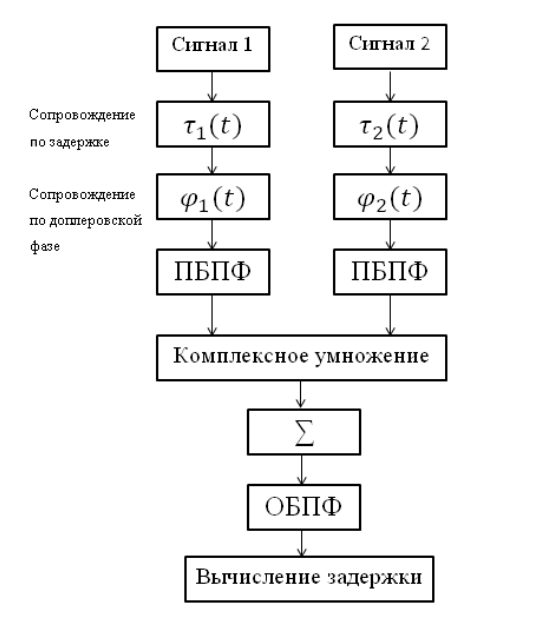
دائرة الارتباط المعطاة ، والتي تشمل الكتل التالية:

تحويل فورييه السريع المباشر (PBPF) وتحويل فورييه العكسي (OBPF) ؛
تعويض عن التأخير الذي سبق تقديمه ؛
تعويض تأثير دوبلر.
الضرب معقدة من اثنين الأطياف.
جمع التطبيقات المتراكمة.

نموذج إشارة الملاحة

الأكثر ملاءمة لقياسات VLBI هي إشارات الملاحة للمركبة الفضائية لأنظمة الملاحة عبر الأقمار الصناعية ، مثل GPS و GLONASS. يتم فرض عدد من المتطلبات على إشارات الملاحة:

تسمح لك لتحديد pseudorange جيدا ؛
نقل المعلومات حول موقف نظام الملاحة ؛
يمكن تمييزها عن إشارات NS الأخرى ؛
لا تتداخل مع أنظمة الراديو الأخرى ؛
لا تتطلب معدات معقدة لاستقبال ونقل.

راضون إلى حد ما عن إشارة مع تعديل الطور الثنائي (ثنائي الموضع) - BPSK (مفتاح إزاحة الطور الثنائي) ، والذي يشار إليه في الأدب الروسي باسم FM-2. يغير هذا التشكيل مرحلة تذبذب الموجة الحاملة بمقدار π ، والتي يمكن تمثيلها على النحو التالي:

$S (t) = A \ cdot cos (t) \ cdot cos (2 \ pi ft) ،$

حيث G (t) هي وظيفة التشكيل.

لتنفيذ تعديل الطور ، يمكن استخدام مولدين ، كل منهما يشكل التردد نفسه ، ولكن مع مرحلة أولية مختلفة. تتيح لك وظيفة التعديل توسيع طيف الإشارة وقياس الحيلة الزائفة بدقة (المسافة بين القمر الصناعي والمستقبل ، وتحسب حسب وقت نشر الإشارة دون تصحيح للفرق بين ساعة القمر الصناعي والمستقبل).

فيما يلي قائمة توضح المبادئ الأساسية لـ BPSK:

إدراج

from scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2; #f  fs = 100; #    t = arange(0,1,1/fs) #    1 / fs #      BPSK p1 = 0; p2 = pi; #     N =12#     #   bit_stream=np.random.random_integers(0, 1, N+1) #   time =[]; digital_signal =[]; PSK =[]; carrier_signal =[]; #  for ii in arange(1,N+1,1): #   if bit_stream [ii] == 0: bit = [0 for w in arange(1,len(t)+1,1)]; else: bit = [1 for w in arange(1,len(t)+1,1)]; digital_signal=hstack([digital_signal,bit ]) #  BPSK if bit_stream [ii] == 0: bit = sin (2*pi*f*t+p1); else: bit = sin (2*pi*f*t+p2); PSK=hstack([PSK,bit]) #   carrier = sin (2*f*t*pi); carrier_signal = hstack([carrier_signal,carrier]) ; time = hstack([time ,t]); t=t+1 suptitle("    (BPSK)") subplot (3,1,1); plot(time,digital_signal,'r'); grid(); subplot (3,1,2); plot (time,PSK); grid(); subplot (3,1,3); plot (time,carrier_signal); grid() show() figure() title("     (BPSK)") n = len(PSK) k = np.arange(n) T = n/fs frq = k/T frq = frq[np.arange(int(n/2))] Y = fft(PSK)/n Y = Y[range(n //2)] / max(Y[range(n // 2)]) plot(frq[75:150], abs(Y)[75:150], 'b')#    grid() #   PSK  scales = scg.periods2scales( arange(1, 40)) ax2 = scg.cws(PSK, scales=scales, figsize=(6.9,2.9)); show()

نحصل على:

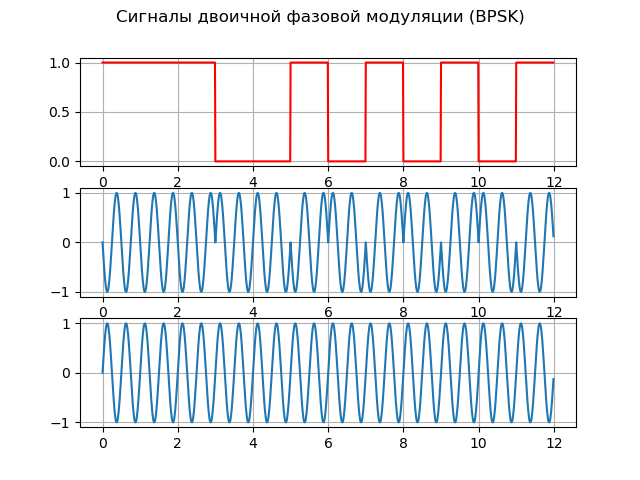
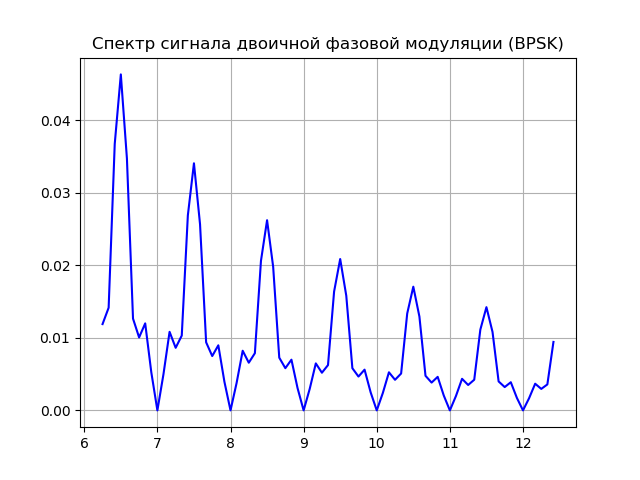
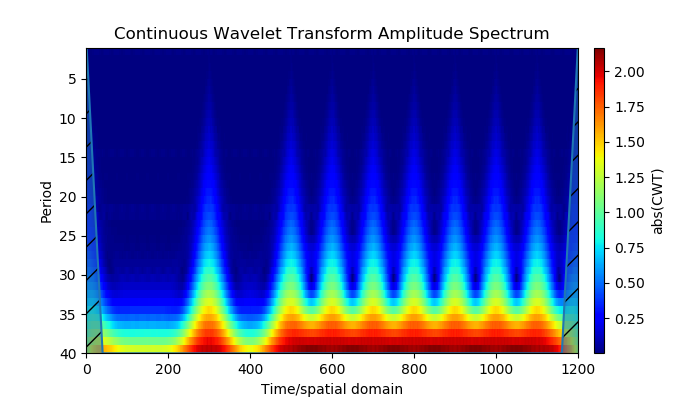
نموذج المصدر

للإشارة التوافقية الملاحية الطورية من القمر الصناعي أو المركبة الفضائية الشكل:

$x = a (2 \ pi f_ {c} t + \ sum s_ {n} cos (2 \ pi f_ {n} t)) ،$

أين هو تردد الناقل

$f_ {c} = 8.4 دولا$ غيغاهيرتز.

تحتوي الإشارة على العديد من المعلمات الخاضعة للرقابة: سعة التذبذب المشكَّل nth

$s_ {n}،$ تردده

$f_ {c}$ وسعة الناقل التذبذب أ.

للحصول على وظيفة الارتباط التي يتم فيها كبح الفصوص الجانبية قدر الإمكان ويتم الوصول إلى أضيق ذروة ارتباط ، سنقوم بتغيير قيم التردد باستخدام قيم 2 و 4 و 8 و 16 MHz ، ومؤشر التشكيل في المدى من 0 إلى 2 في زيادات قدرها π. اسمحوا لي أن أقدم لك قائمة بالبرنامج لإجراء هذا البحث عن معلمات دالة مضبوطة على مراحل للنتيجة النهائية:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**18 #-  delay =4 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fs = (N - 1)/T #  ax = 1e-3 bx = 2e-6 ay = 2e-3 by = 3e-6 aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 taux = ax + bx*t1 tauy = ay + by*t2 tauex = aex + bex*t1 tauey = aey + bey*t2 #  # print(" :") No1 = No2 = 0 fc = 8.4e9 #  #   A1 = 2*pi A2 = 0 A3 =2*pi A4 = 4*pi #   fm1 = 2e6 fm2 = 4e6 fm3 = 8e6 fm4 = 16e6 f = 20e6 #     ff = fc - f #   fco = 16e6 #     def korel(x,y): #  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s #   def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s # def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t) # def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N return sqrt(z.real**2 + z.imag**2) #   def graf(c, t): c1=c[int(N/2):N] c2=c[0:int(N/2)] C = concatenate((c1, c2)) xlabel(',') ylabel('') title('   ') grid(True) plot(t*1e9 - 250, C, 'b',label="    \n    ") legend(loc='best') show() noise1 = random.uniform(-No1, No1, size = N) #   noise2 =noise1 #   x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1) y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2) n = 100001 #  #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) x2 = filt(x1) y2 = filt(y1) X2 = phase_shifter2(x2, t1, tauex, bex) Y2 = phase_shifter2(y2, t2, tauey, bey) Corr = corr(X2, Y2) graf(Corr, t1) #     ##for A1 in [pi/4,pi/2,pi]: ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)) ## y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)) ## korel(x,y) ##for fm in [ fm2,fm3,fm4]: ## A1=2*pi ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm*t1)) ## y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm*t2)) ## korel(x,y) #     ##for fm2 in [ fm1, fm2,fm3,fm4]: ## A1=2*pi ## A2=2*pi ## fm1=2e6 ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)) ## y =cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)+A2*np.cos(2*pi*fm2*t2)) ## korel(x,y) x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)+A3*cos(2*pi*fm3*t1)+A4*cos(2*pi*fm4*t1)) y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2) +A2*cos(2*pi*fm2*t2) +A3*cos(2*pi*fm3*t2)+A4*cos(2*pi*fm4*t2)) korel(x,y)

نحصل على:

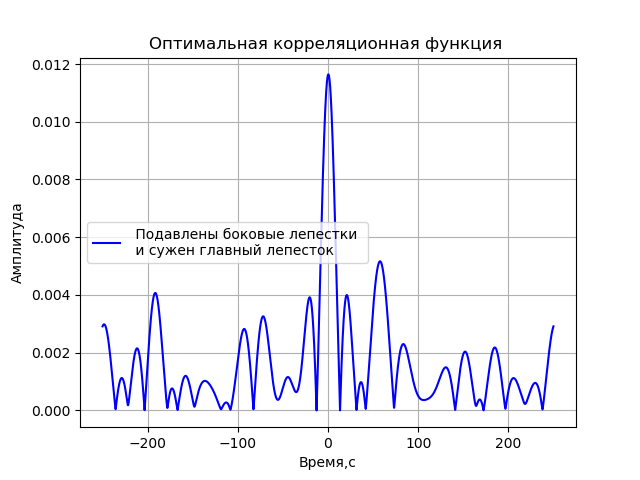
الوظيفة الناتجة لها النموذج:

$x = cos (2 \ pi f_ {c} t + 2 \ pi cos (2 \ pi 10 ^ {6} t) +2 \ pi cos (2 \ pi 10 ^ {8} t) +4 \ pi cos (2 \ pi 10 ^ {16} t)). (1) دولا$

علاوة على ذلك ، سيتم استخدام هذه الوظيفة لمحاكاة VLBI.

نموذج لمولد ضوئي يحاكي التداخل الذي يتم استقباله مع إشارة من الفضاء ومن الغلاف الجوي للأرض

يمكن تطبيق وظيفة (1) لإشارة التنقل المشكَّلة على الطور على كلتا قناتي مقياس التداخل الراديوي ، لكن من الضروري مراعاة تأخير الإشارة في القناة الثانية والضوضاء في كلتا القناتين كما هو موضح في القائمة التالية:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  delay =1e-7 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9 #  # print(" :") No1 = No2 = 0.5 noise1 = random.uniform(-No1, No1, size = N) #   noise2 =random.uniform(-No1, No1, size = N) #   x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) title("    \n    ") plot(t1,x,label="  ") plot(t2,y,label="  c ") x=noise1;y=noise2 plot(t1,x,label="  ") plot(t2,y,label="  ") legend(loc='best') grid(True) figure() noise1_2 = np.random.uniform(-No1, No1, size = N) #     sko=np.std(noise1_2) mo= np.mean(noise1_2) sko=round(sko,2) mo=round(mo,2) title("  . :%s,:%s"%(sko,mo)) ylabel('   ') xlabel('  ') hist(noise1_2,bins='auto') show()

نحصل على:

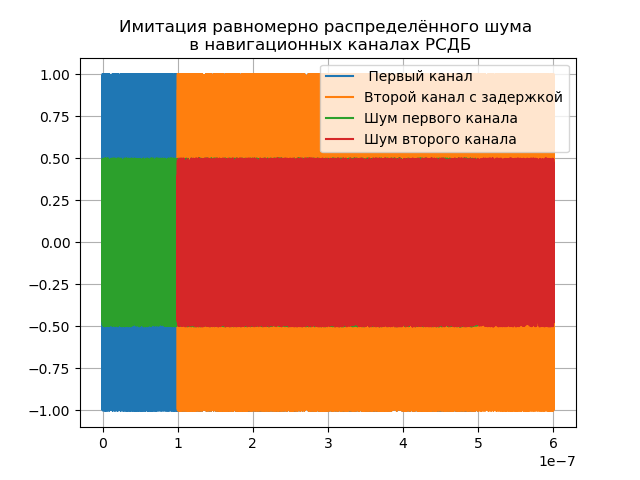
يتم تعيين تأخير التأخير = 1e-7 للعرض ، وهو في الواقع يعتمد على القاعدة ويمكن أن يصل إلى أربع وحدات أو أكثر.

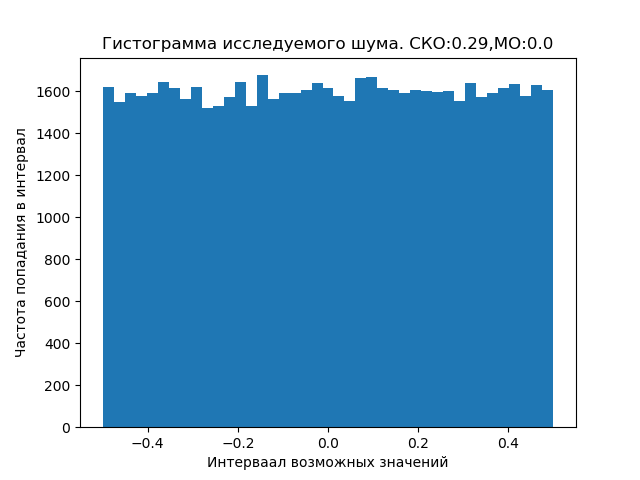
يمكن توزيع الضوضاء على حد سواء الكونية والأرض القريبة وفقًا لقانون مختلف عن الزي المدرسي المحدد ، والذي يتطلب دراسات خاصة.

نمذجة تأثير دوبلر

نظرًا لحقيقة أن الأرض لها شكل دائري وتدور حول محورها ، تصل الإشارات من الفضاء إلى الهوائيات بتأخير مختلف. لهذا السبب ، من الضروري تحويل الإشارات في الوقت المناسب ومراعاة تردد دوبلر. سنعتبر أن التأخير يختلف وفقًا للقانون الخطي:

$\ tau _ {x} (t) = a_ {x} + b_ {x} t ، (2)$

حيث

$a_ {x} = 1..3 \ cdot 10 ^ {- 3}$ مللي و

$b_ {x} = 1..3 \ cdot 10 ^ {- 6}$ مللي ثانية. تم العثور على مرحلة دوبلر كمشتق للتأخير:

$f_ {dx} = \ frac {d \ tau (t)} {dt} = b_ {x} ، (3)$

يجب أن تبدو الإشارة المستلمة:

$\ hat {x} = x (t- \ tau _ {x}) e ^ {j2 \ pi f_ {dx} t} ،$
حيث x (t) هي الإشارة المشعة من المركبة الفضائية.

يتم عرض مظاهرة لتأثير دوبلر في القائمة التالية:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s.real figure() title("    ") ax = 3e-3 bx = 3e-6 taux = ax + bx*t1 x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) sx=phase_shifter1(x, t1, taux, bx ) plot(t1[0:150],x[0:150],label="      ") plot(t1[0:150],sx[0:150],label="      ") grid(True) legend(loc='best') figure() title("    ") ay = 2e-3 by = 3e-6 tauy = ay + by*t2 y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) sy= phase_shifter1(y, t2, tauy, by) plot(t2[0:150],y[0:150],label="      ") plot(t2[0:150],sy[0:150],label="      ") grid(True) legend(loc='best') show()

نحصل على:

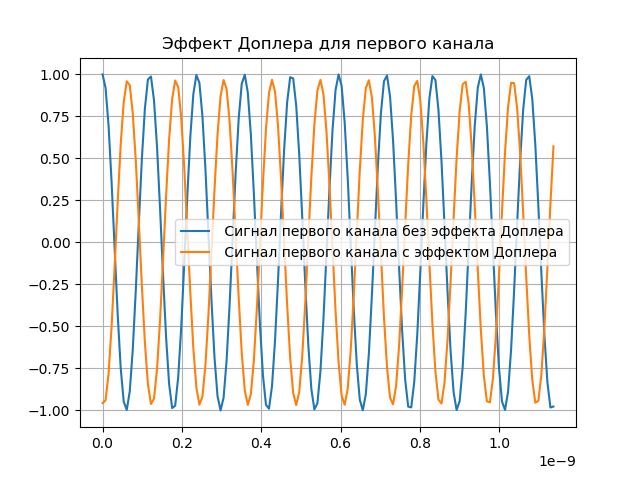
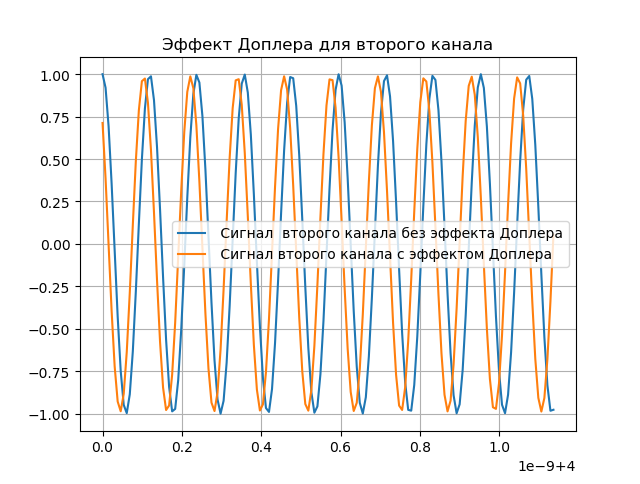
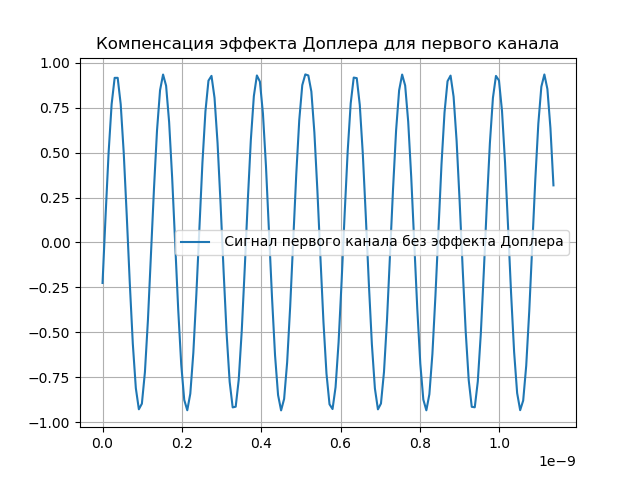
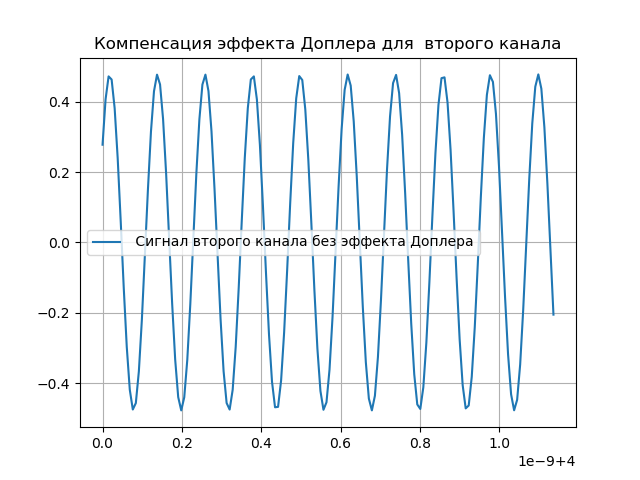
نمذجة تعويض دوبلر

من الواضح ، يجب تعويض التغييرات التي تم إجراؤها على الإشارة. لهذا الغرض ، يحتوي النظام على دعم لمرحلة التأخير ودوبلر. بعد مرور الإشارة عبر نظام التسجيل ، يتم تقديم تأخير:

$\ tau _ {ex} (t) = a_ {x} + b_ {ex} t ، (4)$

سيعتبر أن التأخير يحسب بدقة معينة ، بحيث

$\ اليسار | a_ {ex} -a_ {x} \ right | <30$ نانوثانية

$\ اليسار | b_ {ex} -b_ {x} \ right | <10$ ns ، أي سيكون مختلفًا بعض الشيء عن التأخيرات السابقة. من الواضح أن التأخير يتم تقديمه بعلامة معاكسة مما تم تقديمه مسبقًا.

ستبدو الإشارة المستلمة:

$\ hat {x} = \ tilde {x} (t + \ tau _ {ex}) e ^ {- j2 \ pi f_ {de} t}. (5) دولا$

يتم عرض تعويض تأثير Doppler في القائمة التالية:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s.real ax = 3e-3 bx = 3e-6 taux = ax + bx*t1 x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) sx=phase_shifter1(x, t1, taux, bx ) ay = 2e-3 by = 3e-6 tauy = ay + by*t2 y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) sy= phase_shifter1(y, t2, tauy, by) def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s.real figure() title("     ") aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 tauex = aex + bex*t1 x1 = phase_shifter2(sx, t1, tauex, bex) plot(t1[0:150],x1[0:150],label="      ") grid(True) legend(loc='best') figure() title("     ") aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 tauey = aey + bey*t2 y2 = phase_shifter2(sy, t2, tauey, bey) plot(t2[0:150],y2[0:150],label="      ") grid(True) legend(loc='best') show()

نحصل على:

محاكاة heterodyne الإشارة

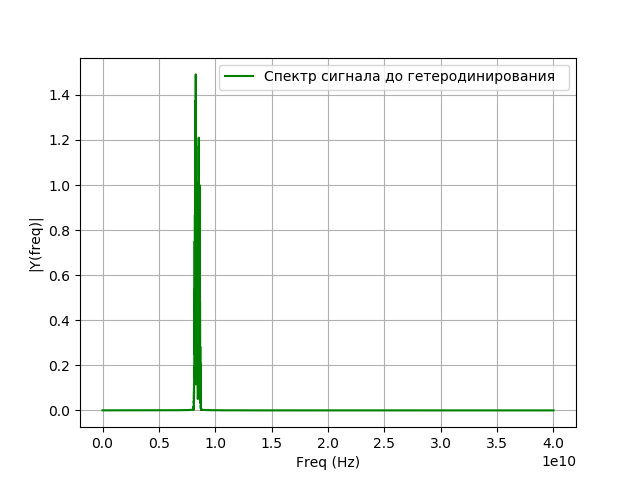
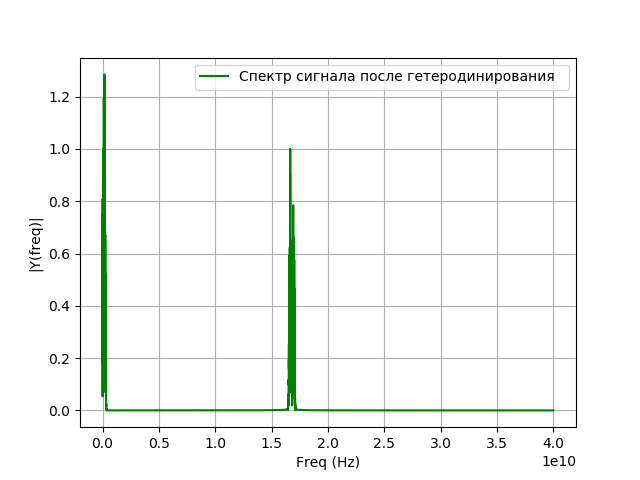
بعد دخول الإشارة إلى نظام التسجيل ، يحدث تحويل التردد ، والذي يُطلق عليه أيضًا اسم heterodyning. هذا هو تحول غير خطي فيه أي من إشارات ترددين مختلفين

$f_ {1}$ و

$f_ {2}$ يتم تمييز إشارة تردد الفرق -

$f = \ اليسار | f_ {1} -f_ {2} \ right. |$ سيكون تردد إشارة المذبذب المحلي مساوياً للفرق بين تردد الإشارة التي تم التحقيق فيها والتردد الذي ترغب في الحصول عليه بعد النقل. يتم تنفيذ التغاير باستخدام مولد مساعد للتذبذبات التوافقية - مذبذب محلي وعنصر غير خطي. رياضيا ، عدم التجانس هو ضرب الإشارة بواسطة الأس:

$x_ {g} = \ hat {x} e ^ {j2 \ pi f_ {g} t} ، (6)$
حيث

$f_ {g}$ - إشارة مذبذب المحلية.

برنامج التغاير:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) a=fs;b=0;c=20000;e='g'; st='     ' spectrum_wavelet(x,a,b,c,e,st) show()

نحصل على:

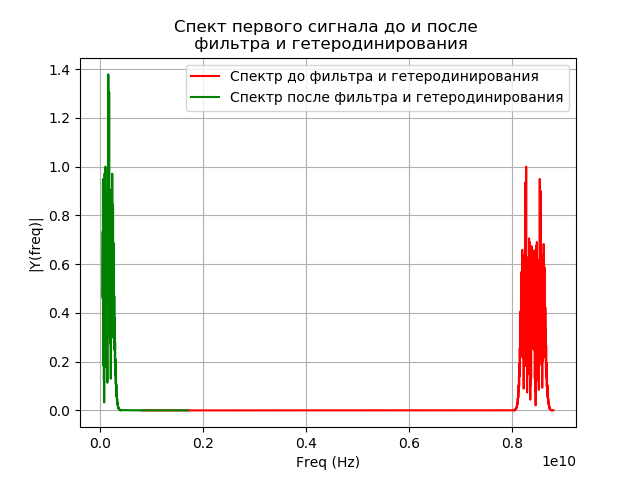
نمذجة تصفية إشارة بعد heterodyning

بعد التجانس ، تدخل الإشارة في مرشح ممر الموجة. عامل تصفية مرور (PP)

$f_ {pass} = 32 دولا$ ميغاهيرتز. يتم حساب استجابة الاندفاع للمرشح بواسطة طريقة النافذة باستخدام وظيفة مكتبة الإشارة. للحصول على إشارة عند إخراج المرشح ، يتم تنفيذ الإلتفاف للمرشح والإشارة في المجال الزمني. الإلتواء المتكامل لحالتنا يأخذ الشكل:

$\ check {x} (t) = \ int _ {- \ infty} ^ {+ \ infty} x_ {g} (t) h (t- {t} ') dt ، (7)$

حيث h (t) هي استجابة الاندفاع للمرشح.

تم العثور على الالتواء باستخدام وظيفة مكتبة الإشارات. يتم تقديم الإشارة المسجلة ، مع مراعاة عدم التجانس والترشيح ، في شكل صيغة

$\ check {x} (t) = (\ hat {x} (t) e ^ {- j2 \ pi f_ {g} t}) * h$

حيث يشار إلى الإلتواء ب *.

برنامج نمذجة الترشيح:

Listinng

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t).real z=heterodyning(x, t1) fco = 16e6 #     n = 100001 #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y q=filt(z) a=fs;b=0;c=850;e='g'; st='    ' spectrum_wavelet(q,a,b,c,e,st) show()

نحصل على:

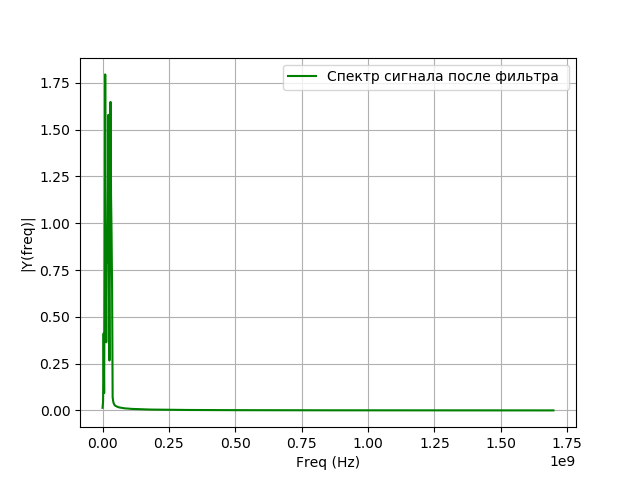
تستخدم محولات الإشارة الرقمية لـ VLBI بشكل أساسي المرشحات ذات الاستجابة النبضية المحدودة (FIR) ، نظرًا لوجود عدد من المزايا بالمقارنة مع المرشحات ذات استجابة النبض اللانهائية (IIR):

يمكن أن تحتوي مرشحات FIR على استجابة طرفية صارمة في حالة تناظر الاستجابة النبضية (IM). وهذا يعني أنه باستخدام مثل هذا المرشح ، يمكن تجنب تشوهات الطور ، وهو أمر مهم بشكل خاص لقياس التداخل الراديوي. لا تحتوي عوامل التصفية ذات الاستجابة النبضية اللانهائية (IIR) على خصائص التناظر الخاصة بـ THEM ولا يمكن أن تحتوي على استجابة للطور الخطي.
مرشحات FIR غير متكررة ، مما يعني أنها مستقرة دائمًا. لا يمكن ضمان استقرار مرشحات IIR دائمًا.
النتائج العملية لاستخدام عدد محدود من البتات لتنفيذ المرشحات أقل أهمية بكثير لمرشحات FIR.

في القائمة أعلاه ، يتم تنفيذ نموذج مرشح ممر الموجة FIR باستخدام طريقة النافذة ، تم اختيار ترتيب المرشح بحيث يكون شكل استجابة تردد المرشح قريبًا من مستطيل. عدد معاملات مرشح المحاكاة هو n = 100001 ، أي أن ترتيب المرشح هو P = 100000.

برنامج لبناء استجابة التردد واستجابة المرحلة للمرشح FIR الذي تم الحصول عليه:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   fco = 16e6 #     n = 100001 #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) #  def AFC(A, n, f, deltf, min, max): plot((fftfreq (n, 1./fs)/1e9), 10*log10(abs(fft(A))), 'k') axvline((f - fco)/1e9, color = 'red', label='  ') axvline((f + fco)/1e9, color = 'red') axhline(-3, color='green', linestyle='dashdot') text(8.381, -3, repr(round(-3, 9))) xlabel(', ') ylabel(' , ') title('') grid(True) axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) grid(True) show() #  def PFC(A, n, f, deltf, min, max): plot(fftfreq(n, 1./fs)/1e9, np.unwrap(np.angle(fft(A))), 'k') axvline((f - fco)/1e9, color='red', label='  ') axvline((f + fco)/1e9, color='red') xlabel(', ') ylabel(',') title('') axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) #  grid(True) legend(loc='best') show() AFC(h, n, f, 20e6, -30, 1) PFC(h, n, f, 20e6, -112, 0)

نحصل على:

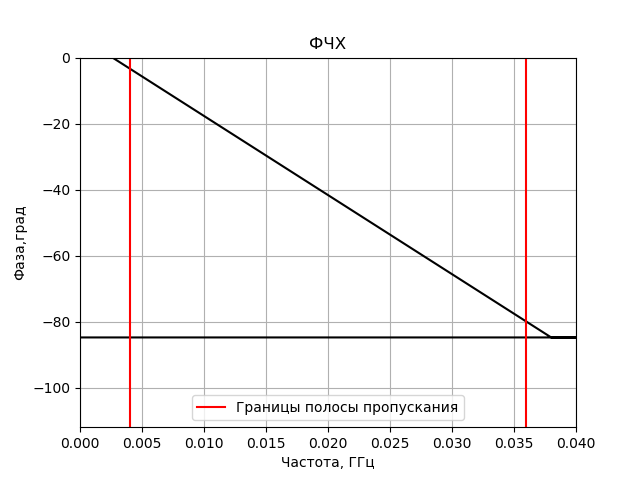
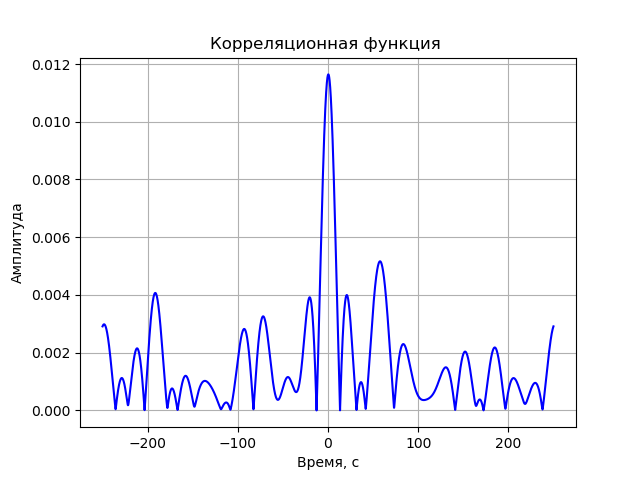
نموذج الارتباط FX

بعد ذلك ، تمر كل إشارة بتحويل فورييه السريع (FFT). يتم تطبيق FFT باستخدام وظيفة مكتبة fft من scipy.fftpack. الأطياف الناتجة معقدة متضاعفة:

$S (j \ omega) = S_ {1} (j \ omega) * S_ {2} (j \ omega) = (a_ {1} + jb_ {1}) * (a_ {2} -jb_ {2} ) = a_ {1} a_ {2} + b_ {1} b_ {2} + j (b_ {1} a_ {2} -a_ {1} b_ {2})$

الإجراء الأخير هو عكس FFT. بما أن سعة دالة الارتباط مهمة ، يجب تحويل الإشارة الناتجة بواسطة الصيغة:

$A = \ sqrt {re ^ {2} + im ^ {2}}$

برنامج وظيفة الارتباط دون مراعاة تشوهات نظام التسجيل:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N q=sqrt(z.real**2 + z.imag**2) c1=q[int(N/2):N] c2=q[0:int(N/2)] C = concatenate((c1, c2)) xlabel(',') ylabel('') title('  ') grid(True) plot(t1*1e9 - 250, C, 'b') show() x= cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) corr(x, y)

نحصل على:

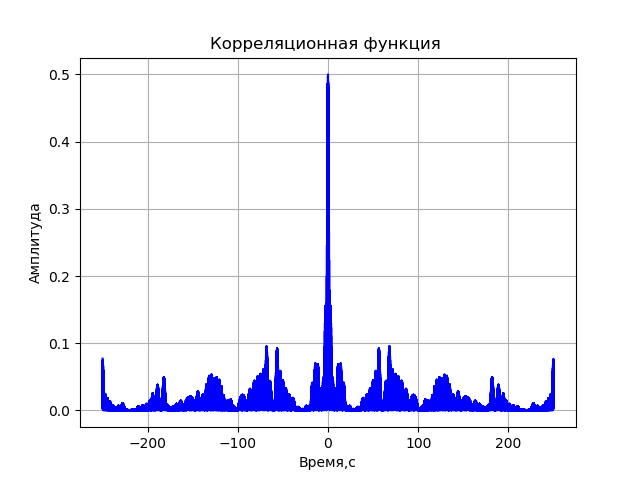
قائمة كاملة من طراز الكمبيوتر من VLBI:

إدراج

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**18 #-  delay =4 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fs = (N - 1)/T #  ax = 1e-3 bx = 2e-6 ay = 2e-3 by = 3e-6 aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 taux = ax + bx*t1 tauy = ay + by*t2 tauex = aex + bex*t1 tauey = aey + bey*t2 #  # print(" :") No1 = No2 = 0 #    # print(" :") fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   fco = 16e6 #     #  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s #   def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s # def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t) # def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N return sqrt(z.real**2 + z.imag**2) #   def graf(c, t): c1=c[int(N/2):N] c2=c[0:int(N/2)] C = concatenate((c1, c2)) xlabel(', ') ylabel('') title('  ') grid(True) plot(t*1e9 - 250, C, 'b') show() noise1 = random.uniform(-No1, No1, size = N) #   noise2 =random.uniform(-No1, No1, size = N) #   def signal_0(): x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) return x,y title(" +  +   ") x,y= signal_0() x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1) plot(x1.real,label="  ") y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2) plot(y1.real,label=" ") grid(True) legend(loc='best') show() n = 100001 #  #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) title("- -    ") x2 = filt(x1) plot(x2.real,label="  ") y2 = filt(y1) plot(y2.real,label="  ") grid(True) legend(loc='best') show() plt.title("      \n   ") a=fs;b=400;c=4400;e='r' st="    " spectrum_wavelet(x,a,b,c,e,st) a=fs;b=20;c=850;e='g' st="    " spectrum_wavelet(x1,a,b,c,e,st) show() X2 = phase_shifter2(x2, t1, tauex, bex) Y2 = phase_shifter2(y2, t2, tauey, bey) Corr = corr(X2, Y2) graf(Corr, t1)

نحصل على:

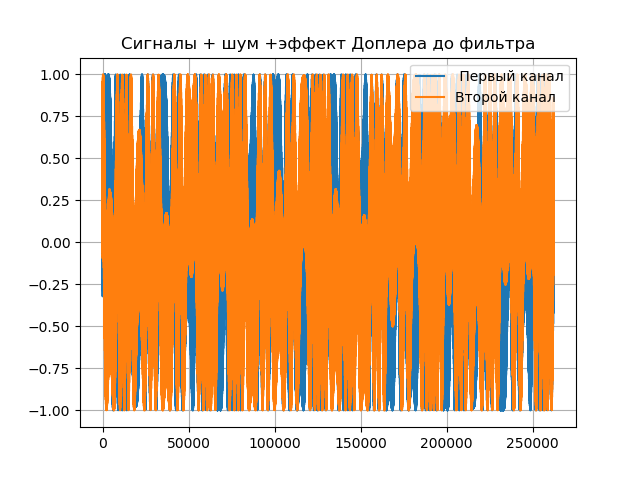
النتائج

ويرد تاريخ موجز لتطور علم الفلك الراديوي.
يتم تحليل الحالة الحالية لشبكات VLBI.
تعتبر المشكلات التي يتم حلها عن طريق شبكات VLBI.
صممت أدوات بايثون نموذجًا لإشارات الملاحة مع تعديل الطور الثنائي (ثنائي الموضع) - BPSK (مفتاح إزاحة الطور الثنائي). يستخدم النموذج تحليل المويجات لتعديل المرحلة.
تم الحصول على نموذج لمصادر الإشارة ، والذي يسمح لأحد بتحديد معلمات التشكيل التي توفر وظيفة الارتباط المثلى وفقًا لمعيار كبح الفصوص الجانبية والحد الأقصى لسعة الفص المركزي.
يتم الحصول على نموذج لشبكة VLBI مبسطة ، مع مراعاة الضوضاء وتأثير دوبلر. يتم النظر في ميزات التصفية باستخدام مرشح ذي استجابة دافعة محدودة.
بعد ملخص موجز للنظرية ، تم تجهيز جميع الطرز ببرامج إيضاحية تتيح لك تتبع تأثير معلمات النموذج.

نموذج رياضي لتلسكوب راديوي طويل المدى

مقدمة

الوضع الحالي لشبكات VLBI

المهام حلها عن طريق VLBI

التنقل في الفضاء باستخدام VLBI

مخطط هيكلي لشبكة VLBI مبسطة

نموذج إشارة الملاحة

نموذج المصدر

نموذج لمولد ضوئي يحاكي التداخل الذي يتم استقباله مع إشارة من الفضاء ومن الغلاف الجوي للأرض

نمذجة تأثير دوبلر

نمذجة تعويض دوبلر

محاكاة heterodyne الإشارة

نمذجة تصفية إشارة بعد heterodyning

نموذج الارتباط FX

قائمة كاملة من طراز الكمبيوتر من VLBI:

النتائج

More articles: