ما زلنا نتحدث عن المؤتمر حول الإحصاءات والتعلم الآلي AISTATS 2019. في هذا المنشور ، سنحلل مقالات حول النماذج العميقة من مجموعات الأشجار ، ونمزج التنظيم للبيانات شديدة التناثر ، والتقريب الفعال للوقت للتوثيق المتبادل.

خوارزمية غابة عميقة: استكشاف لنماذج عميقة غير NN استنادًا إلى وحدات غير قابلة للتمييز
زهي هوا تشو (جامعة نانجينغ)
→ عرض تقديمي
→ المادة
تطبيقات - أدناه
تحدث أستاذ من الصين عن مجموعة الأشجار ، والتي يطلق عليها المؤلفون أول تدريب عميق على الوحدات غير القابلة للتمييز. قد يبدو هذا كأنه بيان صاخب للغاية ، لكن هذا الأستاذ وفهرس H-95 له مدعوون للمتحدثين ، هذه الحقيقة تسمح لنا بأخذ البيان بجدية أكبر. تم تطوير النظرية الأساسية لـ Deep Forest لفترة طويلة ، وكانت المقالة الأصلية هي 2017 (تقريبًا 200 اقتباس) ، لكن المؤلفين يكتبون مكتبات وكل عام يقومون بتحسين الخوارزمية في السرعة. والآن ، يبدو أنهم وصلوا إلى النقطة التي يمكن فيها تطبيق هذه النظرية الجميلة أخيرًا في الممارسة العملية.
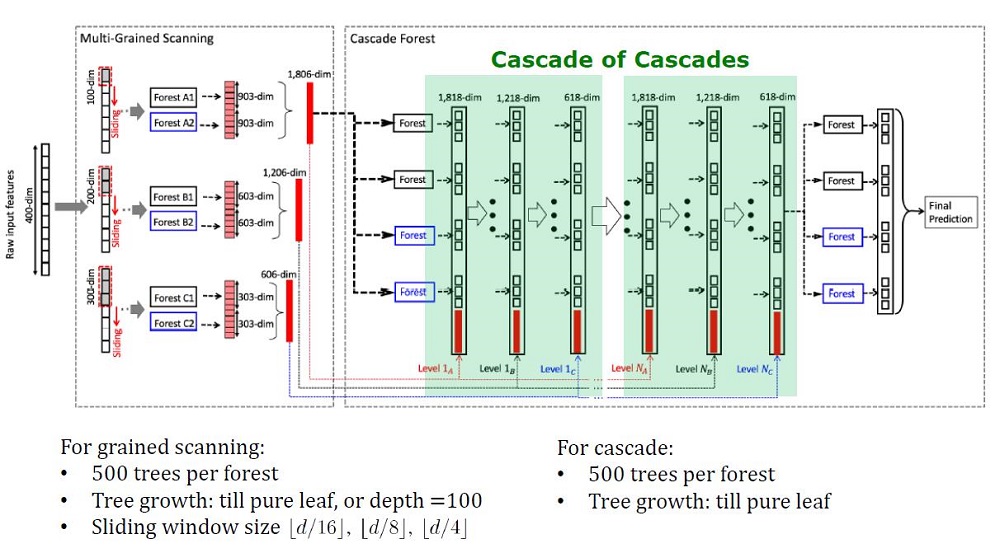
منظر عام لعمارة الغابة العميقة
الشروط
تُستخدم النماذج العميقة ، التي تُفهم الآن على أنها شبكات عصبية عميقة ، لالتقاط تبعيات البيانات المعقدة. علاوة على ذلك ، اتضح أن زيادة عدد الطبقات يكون أكثر كفاءة من زيادة عدد الوحدات في كل طبقة. لكن الشبكات العصبية لها عيوبها:
- يستغرق الكثير من البيانات لعدم إعادة تدريب ،
- يستغرق الكثير من موارد الحوسبة للتعلم في فترة زمنية معقولة ،
- عدد كبير جدًا من البارامترات التي يصعب تكوينها على النحو الأمثل
بالإضافة إلى ذلك ، عناصر من الشبكات العصبية العميقة هي وحدات مختلفة ليست بالضرورة فعالة لكل مهمة. على الرغم من تعقيد الشبكات العصبية ، غالبًا ما تعمل الخوارزميات البسيطة المفاهيمية ، مثل الغابة العشوائية ، بشكل أفضل أو لا تسوء كثيرًا. لكن بالنسبة لهذه الخوارزميات ، تحتاج إلى تصميم الميزات يدويًا ، وهو أمر صعب أيضًا القيام به على النحو الأمثل.
لقد لاحظ الباحثون بالفعل أن المجموعات الموجودة في Kaggle: "مثالية للغاية" ، واستلهمت من كلمات Scholl و Hinton أن التمايز هو أضعف جانب في التعلم العميق ، فقد قرروا إنشاء مجموعة من الأشجار ذات خصائص DL.
الشريحة "كيف تصنع فرقة جيدة"
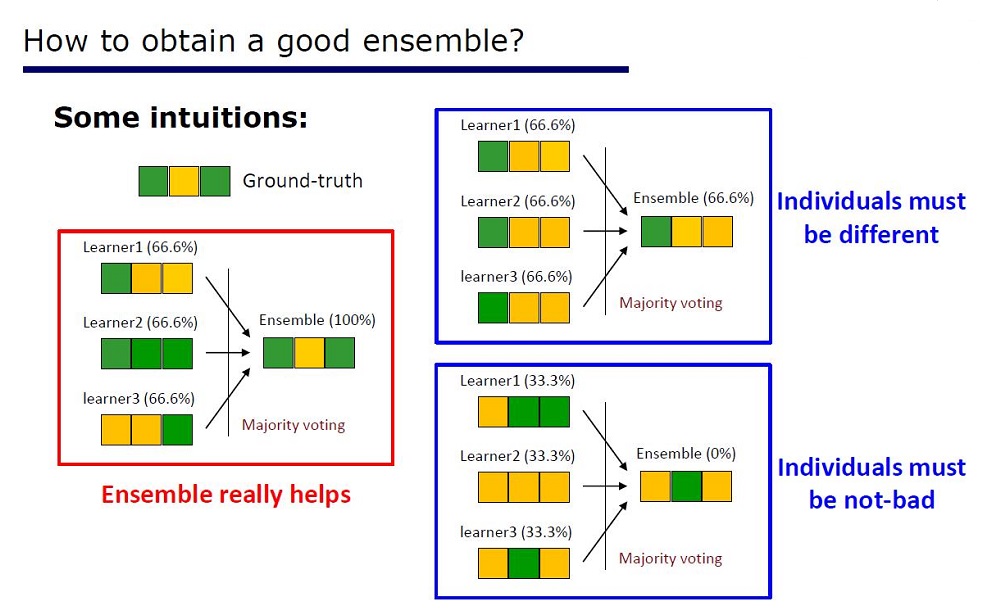
تم استنتاج العمارة من خصائص المجموعات: يجب ألا تكون عناصر المجموعات سيئة للغاية في الجودة وتختلف.
يتكون GcForest من مرحلتين: Cascade Forest و Multi-Grained Scanning. علاوة على ذلك ، حتى لا يعاد تدريب المتتالية ، فهو يتألف من نوعين من الأشجار - أحدهما أشجار عشوائية تمامًا يمكن استخدامها على بيانات غير مخصصة. يتم تحديد عدد الطبقات داخل خوارزمية التحقق من الصحة التبادلية.
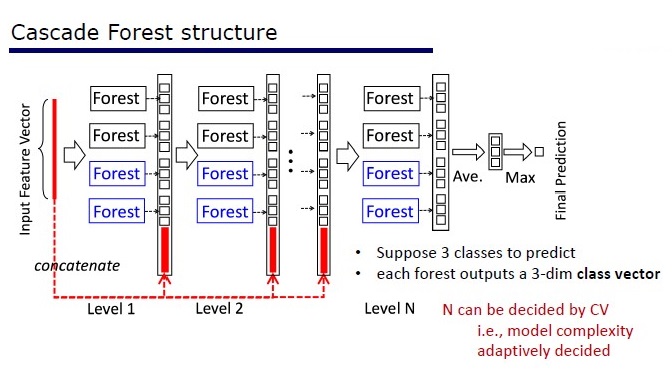
نوعان من الأشجار
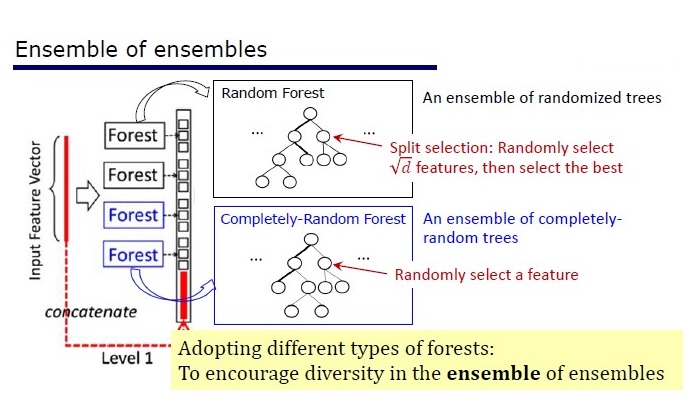
النتائج
بالإضافة إلى النتائج على مجموعات البيانات القياسية ، حاول المؤلفون استخدام gcFestest في معاملات نظام الدفع الصيني للبحث عن الاحتيال وحصلت على F1 و AUC أعلى بكثير من LR و DNN. هذه النتائج موجودة فقط في العرض التقديمي ، ولكن رمز التشغيل على بعض مجموعات البيانات القياسية موجود على Git.
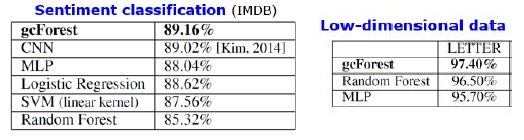
نتائج استبدال الخوارزمية. mdDF هو الأمثل لهامش توزيع أعماق الغابات ، البديل من gcForest
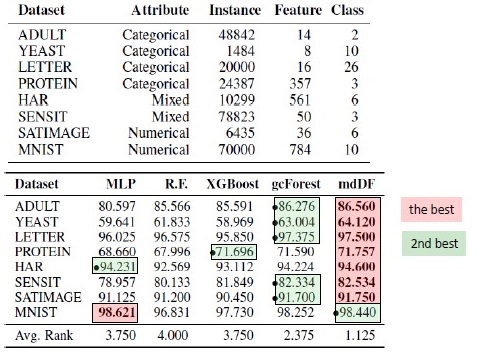
الايجابيات:
- القليل من البارامترات ، يتم ضبط عدد الطبقات تلقائيًا داخل الخوارزمية
- يتم اختيار الإعدادات الافتراضية لتعمل بشكل جيد في العديد من المهام.
- التعقيد التكيفي للنموذج ، على البيانات الصغيرة - نموذج صغير
- لا حاجة لضبط الميزات
- إنه يعمل من حيث الجودة مقارنة بالشبكات العصبية العميقة ، وأحيانًا يكون أفضل
سلبيات:
- لا تسارع على GPU
- في الصور يفقد DNNS
تواجه الشبكات العصبية مشكلة توهين متدرج ، في حين أن الغابات العميقة لديها مشكلة "اختفاء التنوع". نظرًا لأن هذه المجموعة عبارة عن عناصر أكثر "اختلافًا" و "جيدًا" ، كلما زادت الجودة. المشكلة هي أن المؤلفين قد جربوا بالفعل تقريبا جميع النهج الكلاسيكية (أخذ العينات ، والعشوائية). طالما أنه لا يوجد بحث أساسي جديد حول موضوع "الاختلافات" ، فسيكون من الصعب تحسين نوعية الغابات العميقة. لكن من الممكن الآن تحسين سرعة الحوسبة.
استنساخ النتائج
أنا مفتون XGBoost على البيانات الجدولية ، وأردت إعادة إنتاج النتيجة. أخذت مجموعة بيانات البالغين وقمت بتطبيق GcForestCS (نسخة متسارعة قليلاً من GcForest) مع معلمات من مؤلفي المقال و XGBoost مع المعلمات الافتراضية. في المثال الذي كان لدى المؤلفين ، كانت الميزات الفئوية قد تمت معالجتها مسبقًا بطريقة ما ، لكن لم يتم توضيح ذلك. نتيجة لذلك ، استخدمت CatBoostEncoder ومتري آخر - ROC AUC. كانت النتائج مختلفة إحصائيا - فاز XGBoost. وقت تشغيل XGBoost لا يكاد يذكر ، في حين أن gcForestCS لديه 20 دقيقة من كل عملية تحقق مشتركة في 5 أضعاف. من ناحية أخرى ، اختبر المؤلفون الخوارزمية على مجموعات بيانات مختلفة ، وقاموا بتعديل المعلمات لمجموعة البيانات هذه على المعالجة المسبقة لميزاتهم.
رمز يمكن العثور عليها هنا .
تطبيق
→ الكود الرسمي من مؤلفي المقال
→ الرسمية تحسين التعديل ، أسرع ، ولكن لا وثائق
→ التنفيذ أبسط
PcLasso: تجتمع lasso مع الانحدار الرئيسي للمكونات
كينيث تاي ، جيروم فريدمان ، روبرت تيبشيراني (جامعة ستانفورد)
→ المادة
→ عرض تقديمي
→ مثال على الاستخدام
في أوائل عام 2019 ، اقترح ج. كينيث تاي ، وجيروم فريدمان ، وروبرت تيبشيراني من جامعة ستانفورد طريقة تدريس جديدة مع المعلم ، مناسبة بشكل خاص للبيانات المتفرقة.
قام مؤلفو المقالة بحل مشكلة تحليل البيانات حول دراسات التعبير الجيني ، والتي تم وصفها في Zeng & Breesy (2016). الهدف هو الحالة الطفرية للجين p53 ، الذي ينظم التعبير الجيني استجابةً لإشارات مختلفة من الإجهاد الخلوي. الهدف من الدراسة هو تحديد المتنبئين الذين يرتبطون بالحالة الطفيلية لـ p53. تتكون البيانات من 50 صفًا ، 17 منها مصنفة على أنها طبيعية والباقي 33 تحمل طفرات في الجين p53. وفقا للتحليل في سوبرامانيان وآخرون. (2005) 308 مجموعات من الجينات التي تتراوح بين 15 و 500 مدرجة في هذا التحليل. تحتوي مجموعات الجينات هذه على ما مجموعه 4،301 جينًا ومتاحة في حزمة grpregOverlap R. عند توسيع البيانات لمعالجة المجموعات المتداخلة ، يتم إخراج 13،237 عمودًا. استخدم مؤلفو المقال طريقة pcLasso ، مما ساعد على تحسين نتائج النموذج.
في الصورة نرى زيادة في AUC عند استخدام "pcLasso"

جوهر الطريقة
طريقة يجمع  -تنظيم مع
-تنظيم مع  ، الذي يضيق متجه المعاملات إلى المكونات الرئيسية لمصفوفة الميزة. أطلقوا على الطريقة المقترحة "مكونات lasso الأساسية" ("pcLasso" متوفرة على R). يمكن أن تكون الطريقة قوية بشكل خاص إذا تم تجميع المتغيرات مسبقًا (يختار المستخدم ما وكيفية التجميع). في هذه الحالة ، يضغط pcLasso كل مجموعة ويحصل على الحل في اتجاه المكونات الرئيسية لهذه المجموعة. في عملية الحل ، يتم أيضًا اختيار المجموعات المهمة من بين المجموعات المتاحة.
، الذي يضيق متجه المعاملات إلى المكونات الرئيسية لمصفوفة الميزة. أطلقوا على الطريقة المقترحة "مكونات lasso الأساسية" ("pcLasso" متوفرة على R). يمكن أن تكون الطريقة قوية بشكل خاص إذا تم تجميع المتغيرات مسبقًا (يختار المستخدم ما وكيفية التجميع). في هذه الحالة ، يضغط pcLasso كل مجموعة ويحصل على الحل في اتجاه المكونات الرئيسية لهذه المجموعة. في عملية الحل ، يتم أيضًا اختيار المجموعات المهمة من بين المجموعات المتاحة.
نقدم مصفوفة قطرية من التحلل المفرد لمصفوفة مركزية من الميزات  على النحو التالي:
على النحو التالي:
نحن نمثل تحللنا المفرد للمصفوفة المركزية X (SVD) كـ  حيث
حيث  هي مصفوفة قطرية تتكون من القيم الفردية. في هذا النموذج
هي مصفوفة قطرية تتكون من القيم الفردية. في هذا النموذج  - يمكن تمثيل التنظيم:
- يمكن تمثيل التنظيم:
 حيث
حيث  - مصفوفة قطرية تحتوي على وظيفة مربعات القيم الفردية:
- مصفوفة قطرية تحتوي على وظيفة مربعات القيم الفردية: %2C%E2%80%A6%2CZ_%7B22%7D%3Df_2%20(d_1%5E2%2Cd_2%5E2%2C%E2%80%A6%2Cd_m%5E2%20)) .
.
بشكل عام ، في  -regulyarizatsii
-regulyarizatsii  للجميع
للجميع  هذا يتوافق
هذا يتوافق  . يقترحون تقليل الوظائف التالية:
. يقترحون تقليل الوظائف التالية:
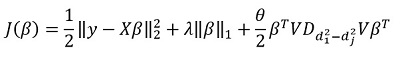
هنا  - مصفوفة اختلافات العناصر القطرية
- مصفوفة اختلافات العناصر القطرية  . بمعنى آخر ، نحن نسيطر على المتجه
. بمعنى آخر ، نحن نسيطر على المتجه  باستخدام hyperparameter أيضا
باستخدام hyperparameter أيضا  .
.
تحويل هذا التعبير ، نحصل على الحل:
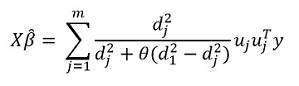
لكن "الميزة" الرئيسية للطريقة ، بالطبع ، هي القدرة على تجميع البيانات ، وعلى أساس هذه المجموعات لتسليط الضوء على المكونات الرئيسية للمجموعة. ثم نعيد كتابة حلنا بالشكل:
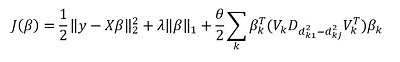
هنا  - ناقلات subvector
- ناقلات subvector  المقابلة للمجموعة ك ،
المقابلة للمجموعة ك ، ) - القيم الفردية
- القيم الفردية  رتبت بالترتيب التنازلي ، و
رتبت بالترتيب التنازلي ، و  - مصفوفة قطرية
- مصفوفة قطرية 
بعض الملاحظات على حل الهدف الوظيفي:
الوظيفة الهدف هي محدبة ، والمكون غير الناعم قابل للفصل. لذلك ، يمكن تحسينه بفعالية باستخدام النسب المتدرج.
النهج هو ارتكاب قيم متعددة  (بما في ذلك الصفر ، على التوالي ، والحصول على المعيار
(بما في ذلك الصفر ، على التوالي ، والحصول على المعيار  -تنظيم) ، ثم تحسين:
-تنظيم) ، ثم تحسين:  التقاط
التقاط  . وفقا لذلك ، المعلمات
. وفقا لذلك ، المعلمات  و
و  يتم اختيار التحقق من الصحة.
يتم اختيار التحقق من الصحة.
معلمة  من الصعب تفسير. في البرنامج (حزمة pcLasso) ، يحدد المستخدم نفسه قيمة هذه المعلمة ، التي تنتمي إلى الفاصل الزمني [0،1] ، حيث 1 يتوافق مع
من الصعب تفسير. في البرنامج (حزمة pcLasso) ، يحدد المستخدم نفسه قيمة هذه المعلمة ، التي تنتمي إلى الفاصل الزمني [0،1] ، حيث 1 يتوافق مع  = 0 (لاسو).
= 0 (لاسو).
في الممارسة العملية ، وتغيير القيم  = 0.25 ، 0.5 ، 0.75 ، 0.9 ، 0.95 و 1 ، يمكنك تغطية مجموعة واسعة من النماذج.
= 0.25 ، 0.5 ، 0.75 ، 0.9 ، 0.95 و 1 ، يمكنك تغطية مجموعة واسعة من النماذج.
الخوارزمية نفسها هي كما يلي

هذه الخوارزمية مكتوبة بالفعل بـ R ، إذا كنت ترغب في ذلك ، فيمكنك استخدامها بالفعل. تسمى المكتبة "pcLasso".
الجيش السويسري Infinitesimal Jackknife
ريان جيوردانو (يو سي بيركلي) ؛ وليام ستيفنسون (MIT) ؛ رانجينغ ليو (جامعة كاليفورنيا في بيركلي) ؛
مايكل جوردان (يو سي بيركلي) ؛ تمارا بروديريك (MIT)
→ المادة
→ رمز
غالبًا ما يتم قياس جودة خوارزميات التعلم الآلي عن طريق التحقق المتبادل المتعدد (التحقق من الصحة أو التمهيد). هذه الطرق قوية ، ولكنها بطيئة في مجموعات البيانات الكبيرة.
في هذا العمل ، يستخدم الزملاء تقريبًا خطيًا للأوزان ، مما ينتج عنه نتائج تعمل بشكل أسرع. يُعرف هذا التقريب الخطي في الأدب الإحصائي باسم "المصارعة بلا حدود". يستخدم بشكل رئيسي كأداة نظرية لإثبات النتائج التقاربية. تكون نتائج المقالة قابلة للتطبيق بغض النظر عما إذا كانت الأوزان والبيانات عشوائية أو حتمية. نتيجةً لذلك ، يقدر هذا التقريب بالتتابع التحقق الحقيقي المتبادل لأي k ثابت.
تقديم الجائزة الورقية لمؤلف المقال

جوهر الطريقة
النظر في مشكلة تقدير معلمة غير معروفة  حيث
حيث  مضغوط ، وحجم مجموعة البيانات الخاصة بنا هو
مضغوط ، وحجم مجموعة البيانات الخاصة بنا هو  . سيتم إجراء تحليلنا على مجموعة بيانات ثابتة. تحديد تصنيفنا
. سيتم إجراء تحليلنا على مجموعة بيانات ثابتة. تحديد تصنيفنا  على النحو التالي:
على النحو التالي:
- لكل منهما
 ، اطلب
، اطلب  (
(  ) هي وظيفة
) هي وظيفة 
 هو رقم حقيقي ، و
هو رقم حقيقي ، و  هو ناقل يتكون من
هو ناقل يتكون من 
ثم  يمكن تمثيلها كـ:
يمكن تمثيلها كـ:

لحل مشكلة التحسين هذه من خلال طريقة التدرج اللوني ، نفترض أن الدوال قابلة للتمييز ويمكننا حساب Hessian. المشكلة الرئيسية التي نحلها هي التكلفة الحسابية المرتبطة بالتقييم ) للجميع
للجميع  . تتمثل المساهمة الرئيسية لمؤلفي المقال في حساب التقدير
. تتمثل المساهمة الرئيسية لمؤلفي المقال في حساب التقدير ) حيث
حيث ) . بمعنى آخر ، فإن تحسيننا يعتمد فقط على المشتقات
. بمعنى آخر ، فإن تحسيننا يعتمد فقط على المشتقات ) التي نفترض وجودها وهيسيان:
التي نفترض وجودها وهيسيان:
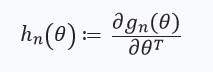
بعد ذلك ، نحدد معادلة ذات نقطة ثابتة ومشتقها:
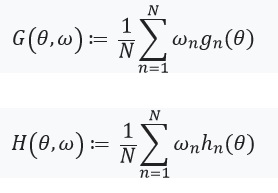
هنا يستحق الاهتمام ذلك %2Cw)%3D0) كما
كما ) - حل ل
- حل ل %3D0) . نحدد أيضا:
. نحدد أيضا: ) ، ومصفوفة الأوزان على النحو التالي:
، ومصفوفة الأوزان على النحو التالي:  . في حالة متى
. في حالة متى  يحتوي على مصفوفة معكوسة ، يمكننا استخدام نظرية الوظيفة الضمنية و "قاعدة السلسلة":
يحتوي على مصفوفة معكوسة ، يمكننا استخدام نظرية الوظيفة الضمنية و "قاعدة السلسلة":
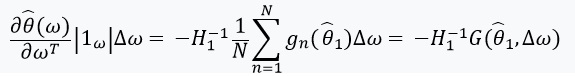
يسمح لنا هذا المشتق بتشكيل تقريب خطي ) من خلال
من خلال  الذي يبدو مثل هذا:
الذي يبدو مثل هذا:
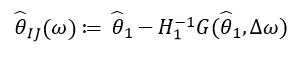
ل  يعتمد فقط على
يعتمد فقط على  و
و  وليس من حلول لأية قيم أخرى
وليس من حلول لأية قيم أخرى  وبالتالي ، ليست هناك حاجة لإعادة حساب وإيجاد قيم جديدة لـ of. بدلاً من ذلك ، يحتاج المرء إلى حل SLE (نظام المعادلات الخطية).
وبالتالي ، ليست هناك حاجة لإعادة حساب وإيجاد قيم جديدة لـ of. بدلاً من ذلك ، يحتاج المرء إلى حل SLE (نظام المعادلات الخطية).
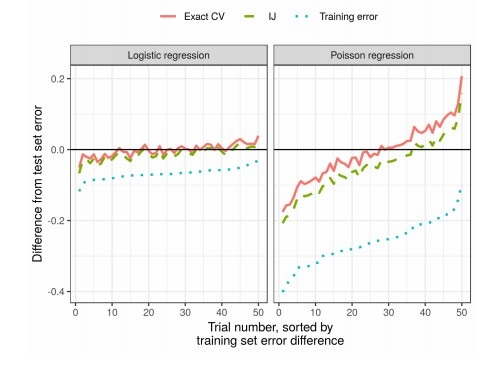
النتائج
في الممارسة العملية ، هذا يقلل بشكل كبير من الوقت مقارنة التحقق من صحة: