أليكسي ساففاتيف: نماذج الإنترنت والشبكات الاجتماعية

"السبب الوحيد لوجود الاقتصاد هو إلهام علماء الرياضيات إلى مآثر جديدة".



في عام 2013 ، ألقى أليكسي ساففاتيف عدة محاضرات حول نماذج الشبكات الاجتماعية والإنترنت. لقد وجدت هذا الموضوع فضوليًا للغاية ونسيه بشكل غير مستحق. دعنا نحاول فهم القضية. أنا مهتم أيضًا بمعرفة كيف تغير الوضع منذ ذلك الحين وما هي المنشورات المفيدة في هذا المجال.

سواء على الإنترنت أو في بيولوجيا الشبكات الاجتماعية ، فإنهم يعرضون خصائص موصوفة بشكل فردي من خلال النماذج ، ولكن معًا - يخلطون بين الرياضيات الحديثة. يدعي سافاتيف أن "الشخص الذي يتعامل مع هذا سيحصل على جائزة نوبل". يعتمد المستقبل على القدرة على العمل مع الشبكات.

ما يلي هو عبارة عن ضغط مترجم لثلاثة مقاطع فيديو للمحاضرات ، في حين أن الفيديو نفسه في النهاية. (يبدو المنشور وكأنه مجموعة من الشرائح مع اقتباسات المحاضر ، لربط كل شيء بنص واحد وأنيق ، أفتقر إلى مهارات اللغة والرياضيات الروسية ، لكن الموضوع مهم للغاية ، لذلك أريد نشره.)

تتكون الشبكة الاجتماعية من:

• وكلاء
• الاتصالات بين الوكلاء

يمكن أن تكون الاتصالات ثنائية الاتجاه (الأصدقاء ، والتأليف المشترك) ، ويمكن أن تكون في اتجاه واحد (مشتركين). كان التواصل الاجتماعي موجودًا دائمًا ، لكن دراستهم على المستوى الكلي أصبحت ممكنة فقط مع ظهور الشبكات عبر الإنترنت. حققت الإنسانية خلال السنوات العشر الماضية قفزة هائلة. لقد تعلمت أن تفحص نفسها ككل. يمكن أن رقمنة. جمع المعلومات عن نفسك.

سيكون من الإنصاف بناء نموذج من الرسوم البيانية الموزونة عند الإشارة إلى معاملات "قوة الرابطة". لكن لنا كما كان من قبل إلى القمر.

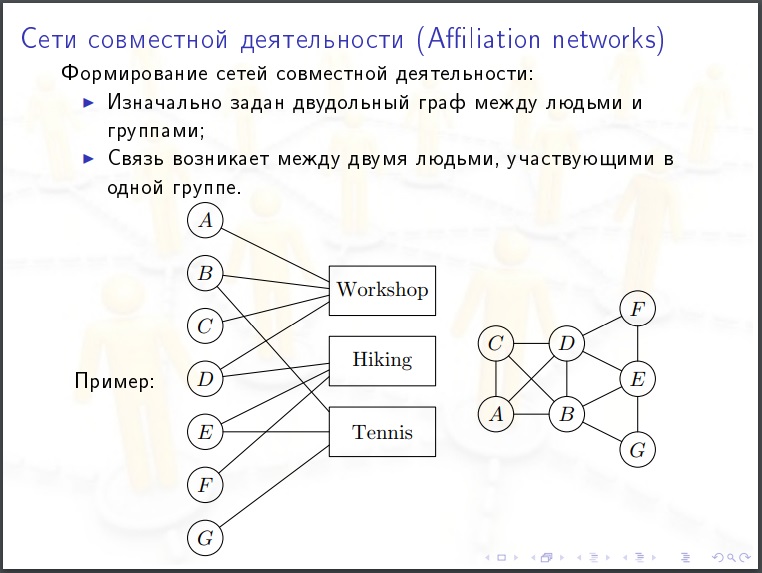
رواق

من المفيد النظر إلى الصور. يمكن أن تكون الفرضية التي يمكنك طرحها بعد عرض الصورة سخيفة بشكل واضح.

من هو مفيد لدراسة الشبكات الاجتماعية

الاقتصاد: هناك افتراض بأن المستويات الجزئية والكلي في الاقتصاد متصلة من خلال "شبكة"
العلوم السياسية: هناك افتراض ما إذا كان النظام سيبقى أو يتغير ، اعتمادًا على من سيكون لديه أخصائيي شبكات أكثر قوة.



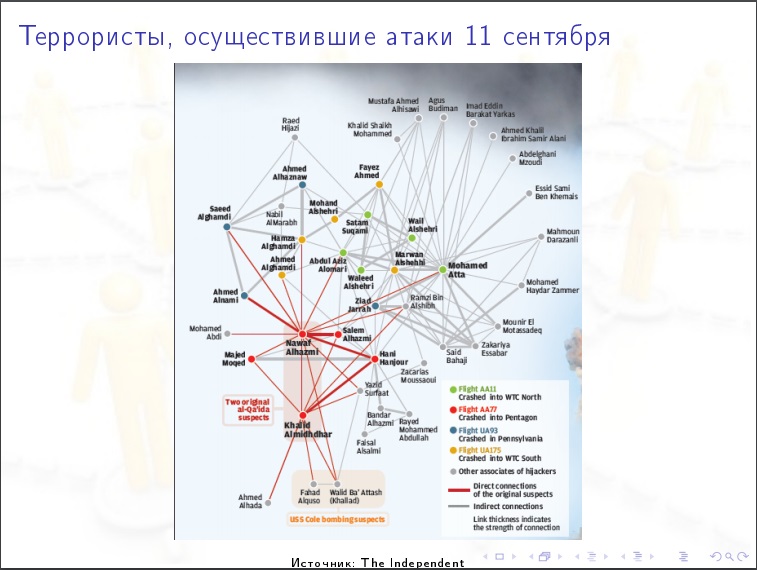مثال تحليلات وسائل التواصل الاجتماعي.

الخصائص العددية للشبكات الاجتماعية

• بعد
• قطر
• درجة قمة الرأس
• توزيع درجة Vertex
• تدابير مركزية العقدة
• توزيع المركزية
• معامل التجميع
• معامل التشكيل

المسافة - كم عدد الحواف التي تحتاج إلى تمريرها للانتقال من قمة إلى أخرى.

القطر هو الحد الأقصى للمسافة في الرسم البياني.

درجة قمة الرأس هي عدد الحواف في قمة الرأس.

نظرية ستة مصافحات

أي رسم بياني اجتماعي له متوسط ​​قطر منخفض للغاية ( نظرية ستة مصافحات ). علاوة على ذلك ، هناك جوهر كثيف جدا. أنا "معتاد" على بعض الأفارقة ، من خلال رئيسي ، الذي صافح الرئيس الإفريقي.







معامل التجميع المحلي . نحن ننظر إلى جميع الجيران للشخص ، قطع "ك". الحد الأقصى للأضلاع - ك (ك -1) / 2. نحن ننظر إلى العدد الفعلي للحواف والقسمة على هذا الحد الأقصى.

عامل التجميع العالمي . كم عدد "المثلثات" مقارنة بـ "العلامات".





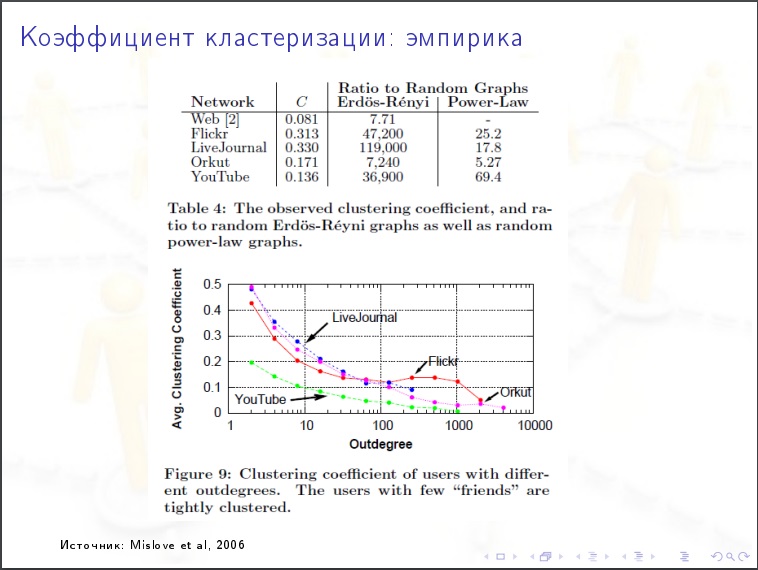توزيع درجة من قمة الرأس . ما هي النسبة المئوية للقمم التي تقل درجاتها عن 1000 هي طبيعة التوزيع الأسي أم الأسي؟ اتضح أن الإنترنت لديه طبيعة رزين.

المعامل هو "2". ستكون القمم التي تكون درجة "x" فيها N / x ² . نحن نتحقق من أنه في مليار مستخدم ، يجب تقسيم الألف من الألف على ألف إلى ألف تربيع. الف الف.

هذا شيء يتناقص ببطء شديد.













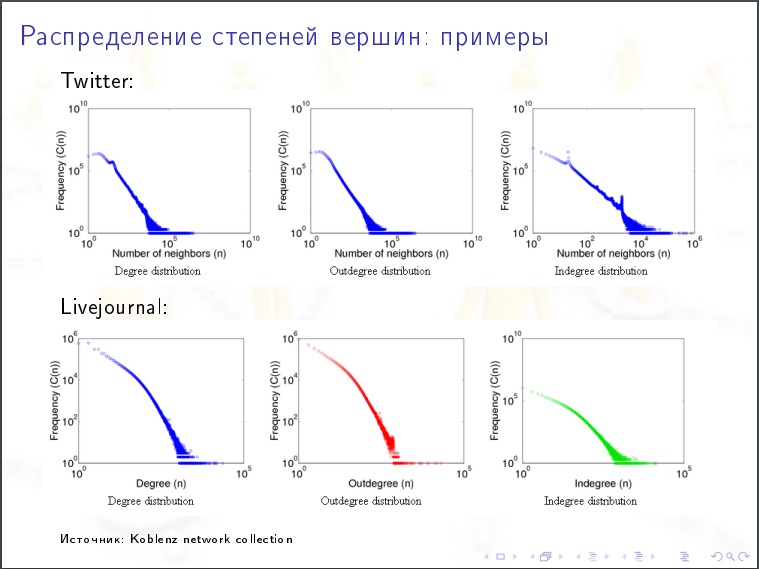
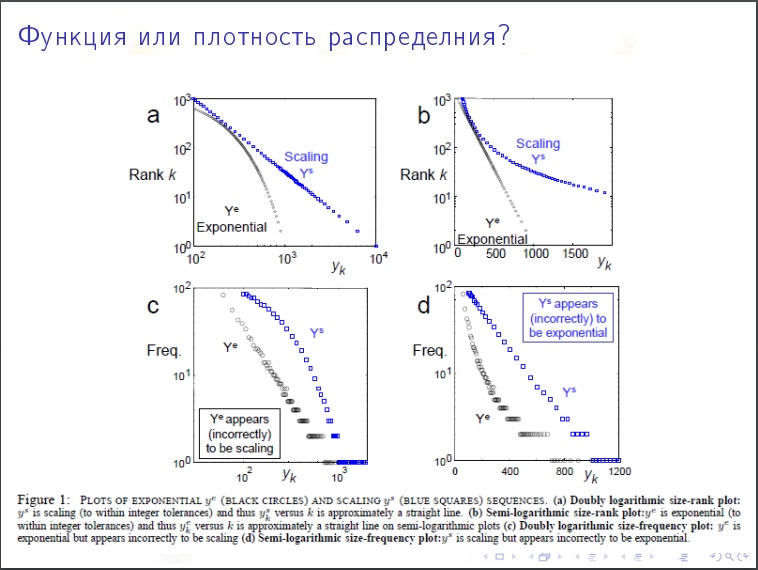
معامل التشكل . نهج تقريبي - نأخذ القمم بنفس عدد الدرجات تقريبًا ، هل من المحتمل أن تكون مرتبطة مع بعضها البعض أم أقل؟ إذا كان الأمر كذلك ، ثم يتم حلها. التشوه - عند وجود عدد كبير من الدرجات تكون على الأرجح أقل. هذا هو النهج الساذج. نهج أكثر صحة هو هذا. في كل قمة ، هناك بعض الخصائص الأخرى (إجمالي رأس مال البنك) ، ويبدو أن هذا المؤشر حسب المجموعة.





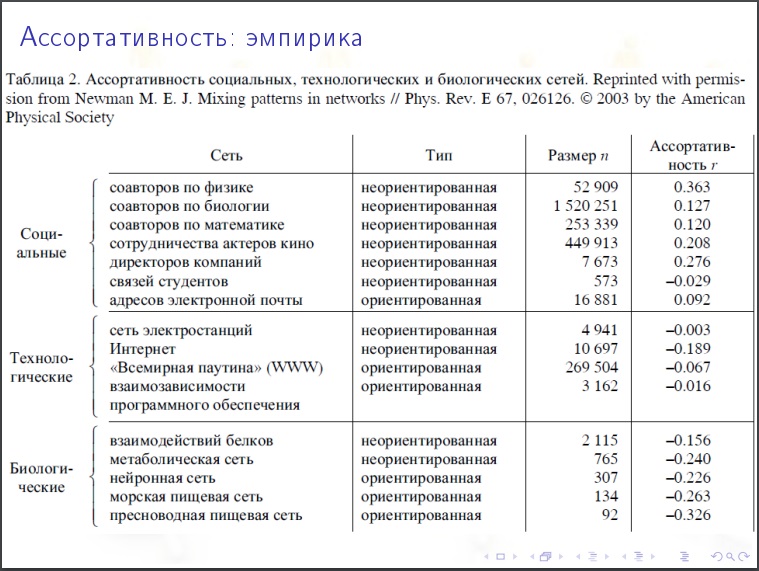مركزية العقدة لشبكة اجتماعية. نحن نأخذ شخصًا ، ونحن نعتبر القيمة التالية له. نقوم بالفرز بين جميع أزواج الأشخاص الآخرين (N-1) (N-2) / 2 وفي كل حالة نسألها ، أقرب مسار مواعدة في الرسم البياني ، هل يمر هذا الشخص؟ قد يكون هناك عدة طرق أقصر وبعضها يحتوي على شخصنا ، ثم نعطيه٪. هذه هي الخاصية الأكثر أهمية في الشبكات الاجتماعية. لانتشار الأوبئة والرأي العام. هذا هو ما يجب قياسه.









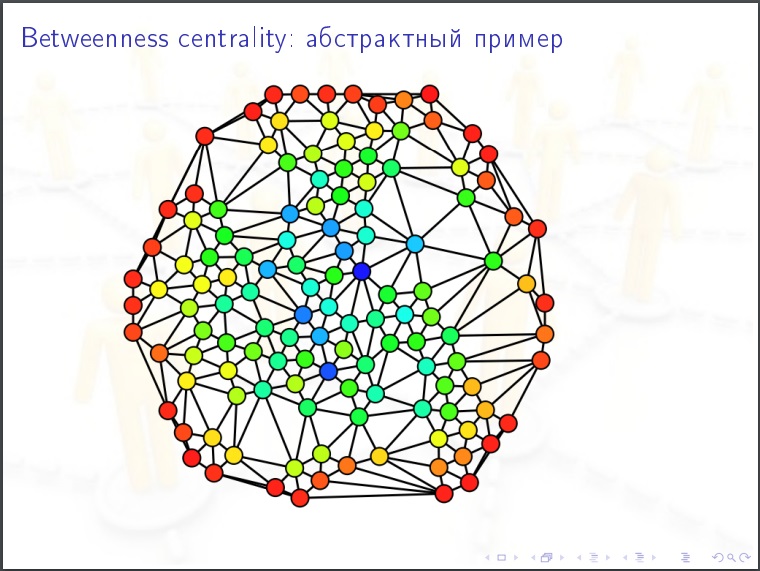
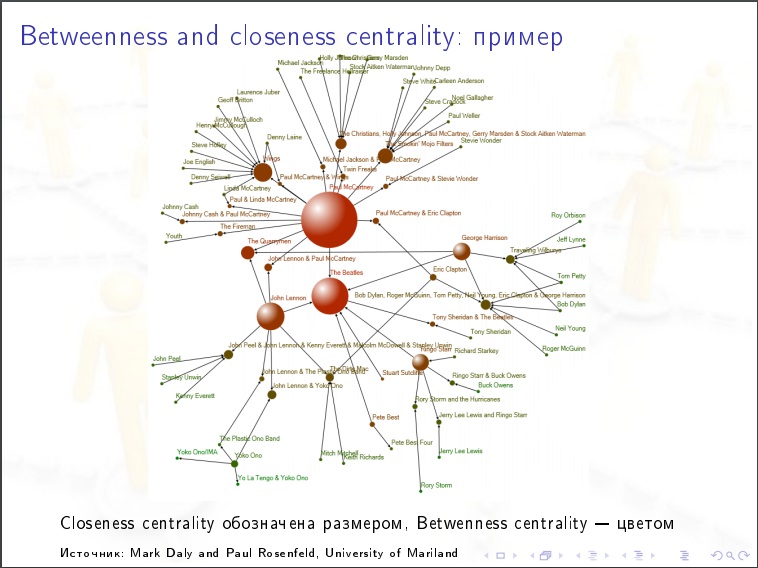
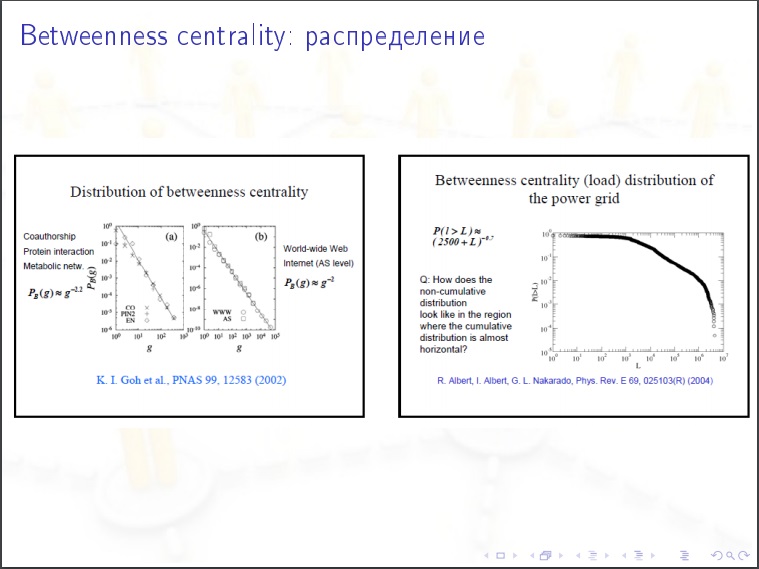
ميزات الشبكات الاجتماعية:

• قطر صغير ومتوسط ​​المسافة بين القمم
• قانون قوة توزيع درجات القمم وبين مركزية المركزية
• ارتفاع نسبة المجموعات
• assortative
• وجود جوهر وثيق الصلة

تتمثل المهمة في إنشاء نموذج يغطي الخصائص الثلاثة الأولى (ويفضل أن يكون الأخيران). الثلاثة الأولى هي بالفعل تعقيد لا يمكن التغلب عليها في هذه المرحلة من الزمن. لعام 2013 ، لا يوجد مثل هذا النموذج.

ننتقل إلى وصف نماذج الرسم البياني العشوائية التي كانت موجودة.

نموذج

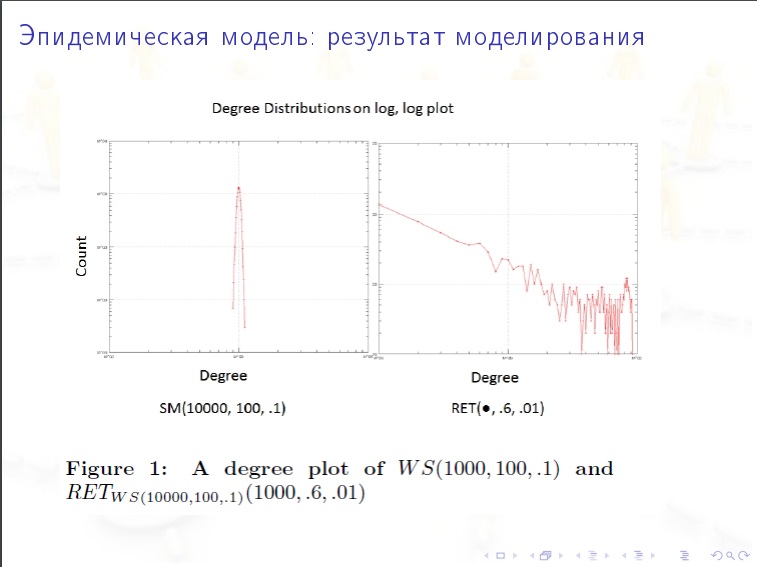
النماذج هي:

• التقنية (يتم إنشاء الحواف بشكل عشوائي)
• نظرية اللعبة (عندما تكون مفيدة لشخص ما)
• بدون هيكل (فقط الكثير من القمم)
• الهيكلية (القمم عبارة عن نقاط ذات مساحة مترية أو لها أوزان ؛ يوجد هيكل على مجموعة القمم)

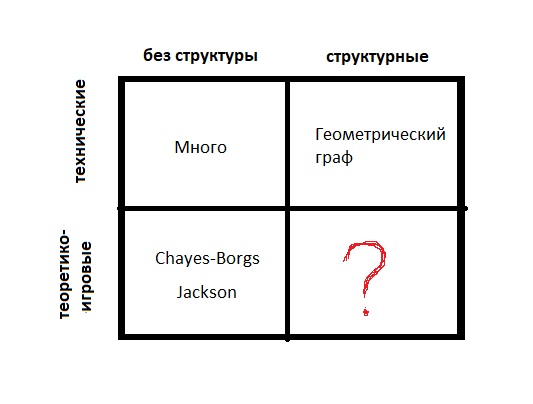
إذا فهمت ما هو الأساس ، فيمكنك الاسترشاد بعدد كبير جدًا من المعلمات. إذا أعطت المعلمات التي تم اختيارها جيدًا تقريبًا جيدًا ، فأنت في حالة جيدة. وحتى إذا كان أفضل مزيج يعطي نتيجة سيئة وغير متسق مع الحقائق التي لوحظت ، ثم وداعا.

كل هذا يتم لغرض واحد - لمكافحة البريد المزعج.

يمكن تخيل الإنترنت كشبكة معقدة على عدة مستويات:

• المستوى التكنولوجي . القمم والحواف عبارة عن خطوط وخطوط اتصال.
• مستوى النص التشعبي . القمم هي مواقع أو صفحات ، والحواف عبارة عن ارتباطات تشعبية.
• المستوى الاجتماعي . القمم هي المستخدمين ، والحواف هي تلك أو غيرها من الروابط بينهم: الصداقات على الشبكات الاجتماعية ، والاشتراك في المدونات ، والتعاون في المشاريع الموزعة (مثل wikipedia) ، إلخ.

بالنسبة إلى الشبكات المعقدة ، تُعرف العديد من الخصائص العددية المحلية والعالمية: توزيع درجات القمم ، معامل التجميع ، معامل التحام

اتضح أن هناك عددًا من الميزات المميزة لشبكات الإنترنت:

• توزيع باريتو للدرجات
• ارتفاع معامل التجميع ،
• صفة إيجابية
• قطر صغير.

الهدف النهائي لنمذجة شبكات الإنترنت هو بناء نماذج لها نفس الميزات.

أردوس موديل - ريني

يعتبر نموذج Erdos - Renyi واحدًا من اثنين من نماذج توليد الرسوم البيانية العشوائية وثيقة الصلة. تم تسمية النماذج باسم عالم الرياضيات Pal Erdös و Alfred Renyi ، اللذين كانا أول من طرح أحد هذه النماذج في عام 1959. استكشاف الرسم البياني التي يرجع تاريخها.

النظر في نقاط N. الحواف المحتملة - N * (N-1) / 2. لكل ضلع نقوم بإجراء اختبار عشوائي. احتمال أن يحدث الضلع - ص. ما لم يحدث - (1 ع). دعنا نجري "الاختبار" ، نحصل على رسم بياني. ولكن هناك بعض المشاكل. لكي تظهر خاصية "sparseness" ، يجب أن تكون p صغيرة جدًا ، بترتيب 1 / N ، وبعد ذلك سيكون القطر كبيرًا جدًا.

أي باحث يسمع أن الإنترنت يوصف بأنه رسم بياني عشوائي وفقًا لنموذج Erds-Renyi سوف يضحك.

تأثير مثير للاهتمام هو أنه عندما تتغلب على عتبة معينة من الاحتمال ، يصبح الرسم البياني متصلاً.

نموذج بولوباشي

هذا نموذج ديناميكي لبناء الإنترنت. نحن نحاول تخمين كيف تشكل تدريجيا. الفكرة هي هذا. نأخذ رسمًا بيانيًا به قمة واحدة وحافة واحدة ، ثم نلعب عشوائياً في كل خطوة. نضيف قمة واحدة ، بعد ذلك ، مع وجود بعض الاحتمالات ، يتم إغلاقه على نفسه ، مع وجود بعض الاحتمالات يتصل بالرقم السابق. الذروة التالية مع بعض الاحتمالات تغلق على نفسها ، والبعض يذهب إلى واحدة من السابقة. علاوة على ذلك ، فإن احتمال ضرب القمة يتناسب دائمًا مع عدد الحواف الموجودة. يتم تشغيل قيمة عشوائية ، ويعتمد السحب التالي على نتيجة السحب السابق. مثل هذا النموذج بديهي ، لكن من الصعب حسابه حسابيًا. هذا النموذج يعطي توزيع الطاقة غير الأسي. القطر هو نفسه.

ولكن هذا النموذج لا يعمل مع المجموعات.

هناك طريقتان متنافستان تعملان مع المجموعات.

النهج الهندسي

الفرضية مأخوذة من السقف. يعتمد الرسم البياني للإنترنت على المساحة المترية. مساحة الأذواق والمصالح والأفضليات. كيف الناس مثيرة للاهتمام لبعضهم البعض. كيف قريبة من الروح ، في الرأي. إذا كان الناس مقربين ، فإنهم يشيرون إلى بعضهم البعض.

نحن نأخذ ونرمي 10 ¹⁰ نقطة في هذا الفضاء. يظهر عدد كبير من المعلمات هنا. ضخمة.

التجميع ممتاز ، لكن الرؤوس المتناقصة هي الأسية. التناقض.

هذه الطريقة بسيطة بشكل رهيب وتتم الخوارزميات "عن طريق الصدفة".

لعبة لعبة بورغز - النظرية

هل تعلم أنه في أيام فون نيومان أعلن أن نظرية اللعبة ستكون سلاح جيل جديد ضد الاتحاد السوفيتي؟

نحن نفترض أن الناس يتخذون قرارات للتواصل مع بعضهم البعض أم لا.

ننظم اجتماعات / أحداث. يعد الحدث قائمة بالضيوف المدعوين ، بالإضافة إلى "شدته".
التكاليف = الكثافة * (ثابت + K * (عدد المدعوين)). يجب أن أنفق الموارد "لبيع" الحدث وعلي إنفاق المزيد على كل مشارك. هناك أعياد ميلاد ، وهناك ارتفاعات. يظهر المعامل "P" ، وهو صغير بالنسبة لعيد الميلاد وكبير في التنزه. يؤرخ كثافة.

يمكن لأي شخص تنظيم العديد من الأحداث بكثافة P ₁ ، P ₂ ... P _n . البعض الآخر يفعل الشيء نفسه.

هناك أفعالي لإقامة علاقات اجتماعية ، وهناك غرباء.

وظيفة الفوز = (عدد الأشخاص الذين أصبحت معهم معرفة جيدة) - التكاليف

يعني "مألوف بما فيه الكفاية" أن مجموع شدة جميع الأحداث التي كنت فيها معًا أكبر من قيمة عتبة معينة. ولا يهم من قام بتنظيم الحدث.

تقام الضلوع لمعارف جيدة بما فيه الكفاية.



ثبت أن العديد من خصائص الإغلاق الحقيقي يتم الحصول عليها في هذا النموذج. في جميع مواضع ناش ، يتم أيضًا ملاحظة خصائص الإغلاق الحقيقية وخصائص التجميع الأقوى ، والتي يتم ملاحظتها أيضًا على الرسم البياني للإنترنت الحقيقي.



ولكن ليس هناك ما هو واضح حول الخصائص الأخرى ، ولكن هذا هو نصف المشكلة. تكمن المشكلة في أنه إذا كان هناك توازن ناش واحد على الأقل يعرف شخصان على الأقل بعضهما البعض ، فهناك توازن ناش يعرفه الجميع.





هناك فكرة للجمع بين النهجين. لاعتبار أن الناس يعيشون في مساحة مترية ، وعندما ينظمون الأحداث ، أو يشاركون في حدث ما ، فإن التكلفة والكثافة ونسب العتبة تعتمد على "القرب". هذا هو الجيل الخامس من النماذج.

تكاليف متباينة

الخيارات هي لجعل التكاليف متباينة والفوز متباينة. بعض الدعوة أسهل من غيرها. التعارف مع أحد أكثر ربحية من التعارف مع الآخر.





لنفترض أننا نرتب جميع الناس بالتساوي حول محيط. ومن الأرخص دعوة شخص أقرب. كيف سيبدو الرصيد؟ الجميع سيدعو بعض الحي ، أليس كذلك؟ غير صحيح لا يوجد مثل هذا التوازن.

برهان. لنفترض أنه موجود ، ثم يتم دعوة الأشخاص المقربين لبعضهم البعض بالفعل إلى العديد من الاجتماعات المختلفة. ثم انه لا يحتاج إلى دعوة هذا الحبيب. وجود هذا التوازن يتناقض مع وجود هذا التوازن.



يوجد توازن نقي ، إنه موجود ، إنه الوحيد. كل يدعو الحي الذي يقع (أو عكس اتجاه عقارب الساعة) على مسافة معينة منه وعلى طول معين.

(- هذا هو تشكيل المجرات!)
(- هذا هو كسر التماثل التلقائي!)

النتائج

كتب بيليفين ذات مرة أن "معنى الحياة الروسية يكمن في التذهيب المذهل للأيقونسطاس الهائل". هذا هو معنى الرياضيات - في نفسه. فقط الأيقونسطوس هو العلم.



هذه دراسة متعددة التخصصات للغاية. أعلى كما يمكنك أن تتخيل.

مصادر

PS

"بمجرد استدعائي للنادي إلى نافالني ، هناك بعض الشباب ، المتحمسين الذين يساعدونه. لقد حذرت على الفور من أن أقول أشياء غير سارة. ثورة منتصرة إذا كان علماء الرياضيات الذين يؤيدون الثورة أقوى من أولئك الذين يعارضون. لم يكن شباب Navalny يعرفون كيفية إخبارهم بهذه النماذج ، لكنهم لا يفهمون ، حتى أنهم لا يعرفون كيفية الاندماج - فهم يركضون ويصرخون في مكان ما. وضدهم يجلسون في معهد قوي به أشخاص جادون على رأسه ، والذي ، بأمر من الكرملين ، يقول من بالضبط وكيف ينبغي القبض عليه حتى لا يكون هناك شيء. يقولون: "نحن لا مركزيون - على وجه التحديد Navalny لا يعني أي شيء ، هناك العديد من القادة المهمين." ثم يأتي عالم الرياضيات ويعتقد أن المركزية هي 90 ٪ من هذه الشبكة. يمكنك حظر شخص ما تحتاجه لبضعة أيام - وليس هناك ثورة. الرياضيات تفوز ".
- أليكسي سافاتيف ، "الثورة تفوز إذا كان لديها علماء رياضيات جيدون"

PPS

من يعرف الأعمال الأخرى المثيرة للاهتمام (المقالات والمحاضرات) التي توجد بها أعمال في مجال الشبكات الاجتماعية وفوائدها العملية ، يرجى المشاركة.