الشبكات العصبية والتعلم العميق ، الفصل 3 ، الجزء 1: تحسين طريقة تدريب الشبكات العصبية

عندما يتعلم الشخص لعب الجولف ، يقضي عادة معظم وقته في تحقيق نجاح أساسي. ثم يقترب من ضربات أخرى ، تدريجيًا ، يدرس هذه الحيل أو تلك ، استنادًا إلى الضربة الأساسية وتطويرها. وبالمثل ، ركزنا حتى الآن على فهم خوارزمية backpropagation. هذا هو "الإضراب الأساسي" ، وهو أساس التدريب لمعظم العمل مع الشبكات العصبية (NS). في هذا الفصل ، سأتحدث عن مجموعة من التقنيات التي يمكن استخدامها لتحسين تطبيقنا الأبسط للطبقة الخلفية ، ولتحسين طريقة تدريس NS.

من بين التقنيات التي سنتعلمها في هذا الفصل ما يلي: الخيار الأفضل لدور دالة التكلفة ، أي دالة التكلفة مع إنتروبيا ؛ أربعة ما يسمى طرق التنظيم (تنظيم L1 و L2 ، استبعاد الخلايا العصبية [التسرب] ، التمديد الاصطناعي لبيانات التدريب) ، والتي تعمل على تحسين تعميم NS لدينا بما يتجاوز حدود بيانات التدريب ؛ أفضل طريقة لتهيئة أوزان الشبكة ؛ مجموعة من الأساليب الإرشادية لمساعدتك في اختيار معلمات جيدة للشبكة. سأدرس أيضًا العديد من التقنيات الأخرى ، بشكل سطحي قليلاً. بالنسبة للجزء الأكبر ، هذه المناقشات مستقلة عن بعضها البعض ، لذلك يمكنك القفز عليها إذا كنت ترغب في ذلك. ننفذ أيضًا العديد من التقنيات في رمز العمل ونستخدمها لتحسين النتائج التي تم الحصول عليها لمهمة تصنيف الأرقام المكتوبة بخط اليد ، والتي تمت دراستها في الفصل الأول.

بالطبع ، نحن نعتبر جزءًا صغيرًا فقط من العدد الهائل من التقنيات المطورة للاستخدام مع الشبكات العصبية. خلاصة القول هي أن أفضل طريقة لدخول عالم الوفرة من التقنيات المتاحة هي دراسة بعض التفاصيل الأكثر أهمية بالتفصيل. إن إتقان هذه التقنيات المهمة ليس مفيدًا في حد ذاته فحسب ، بل سيؤدي أيضًا إلى تعميق فهمك للمشكلات التي قد تنشأ عند استخدام الشبكات العصبية. نتيجة لذلك ، ستكون مستعدًا للتكيف بسرعة مع التقنيات الجديدة حسب الحاجة.

وظيفة التكلفة عبر الانتروبيا

معظمنا يكره كونه مخطئ. بعد وقت قصير من البدء في تعلم البيانو ، قدمت حفلاً صغيراً أمام الجمهور. كنت عصبية ، وبدأت في لعب قطعة أوكتاف أقل من اللازم. كنت في حيرة من أمري ، ولم أستطع المتابعة حتى أشار لي شخص ما خطأ. لقد شعرت بالخجل الشديد. ومع ذلك ، على الرغم من أن هذا غير سارة ، إلا أننا نتعلم أيضًا بسرعة كبيرة ، ونقرر أننا كنا مخطئين. وبالتأكيد في المرة القادمة التي تحدثت فيها مع الجمهور ، لعبت في أوكتاف صحيح! بالمقابل ، نتعلم ببطء أكثر عندما تكون أخطائنا غير محددة جيدًا.

من الناحية المثالية ، نتوقع أن تتعلم شبكاتنا العصبية بسرعة من أخطائها. هل يحدث هذا في الممارسة العملية؟ للإجابة على هذا السؤال ، دعونا نلقي نظرة على مثال بعيد المنال. أنها تنطوي على الخلايا العصبية مع إدخال واحد فقط:



نحن نعلم هذه الخلية العصبية أن تفعل شيئًا بسيطًا يبعث على السخرية: قبول 1 وإعطاء 0. بالطبع ، يمكننا إيجاد حل لمشكلة تافهة من خلال تحديد الوزن والإزاحة يدويًا ، دون استخدام خوارزمية التدريب. ومع ذلك ، سيكون من المفيد للغاية محاولة استخدام النسب المتدرج للحصول على الوزن والتشريد نتيجة التدريب. دعونا ننظر في كيفية تدريب الخلايا العصبية.

من أجل الدقة ، سأختار وزنًا أوليًا قدره 0.6 وإزاحة أولية قدرها 0.9. هذه بعض القيم العامة التي تم تعيينها كنقطة بداية ، ولم أخترها تحديدًا. في البداية ، تنتج الخلايا العصبية الناتجة 0.82 ، لذلك نحتاج إلى معرفة الكثير من أجل الاقتراب من الناتج المرغوب وهو 0.0. تحتوي المقالة الأصلية على نموذج تفاعلي يمكنك من خلاله النقر فوق "تشغيل" ومراقبة عملية التعلم. لم يتم تسجيل هذه الرسوم المتحركة مسبقًا ، حيث يقوم المتصفح بحساب التدرج اللوني ، ثم يستخدمه لتحديث الوزن والإزاحة ، وإظهار النتيجة. سرعة التعلم هي 0.1 = 0.15 ، بطيئة بما يكفي لتكون قادرًا على رؤية ما يحدث ، ولكن بسرعة كافية لتعلم حدوث ذلك في ثوانٍ. دالة التكلفة C من الدرجة الثانية ، مقدمة في الفصل الأول. سأذكرك قريبًا بشكله الدقيق ، لذلك ليس من الضروري أن تعود وتفتش هناك. يمكن بدء التدريب عدة مرات بمجرد النقر على زر "تشغيل".

كما ترون ، فإن الخلايا العصبية تتعلم بسرعة الوزن والانحياز ، مما يقلل التكلفة ، ويعطي ناتجًا 0.09. هذه ليست النتيجة المرجوة تمامًا وهي 0.0 ، لكنها جيدة جدًا. لنفترض أننا اخترنا وزناً أولياً وتعوضنا عن القيمة 2.0 بدلاً من ذلك. في هذه الحالة ، سيكون الناتج الأولي هو 0.98 ، وهذا خطأ تمامًا. دعونا نرى كيف في هذه الحالة سوف تتعلم الخلايا العصبية إنتاج 0.

على الرغم من أن هذا المثال يستخدم نفس معدل التعلم (η = 0.15) ، فإننا نرى أن التعلم أبطأ. حوالي 150 من العصور الأولى والأوزان والتشريد بالكاد تتغير. ثم يتسارع التدريب ، وكما في المثال الأول تقريبًا ، ينتقل العصبونات بسرعة إلى 0.0. هذا السلوك غريب ، وليس مثل تعلم الشخص. كما قلت في البداية ، غالبًا ما نتعلم بسرعة أكبر عندما نكون مخطئين للغاية. لكننا رأينا للتو كيف يتعلم العصب الاصطناعي لدينا بصعوبة كبيرة ، مما يجعل الكثير من الأخطاء - أصعب بكثير مما كان عليه عندما ارتكب خطأ قليلا. علاوة على ذلك ، اتضح أن هذا السلوك لا ينشأ فقط في مثالنا البسيط ، ولكن أيضًا في NS للأغراض العامة. لماذا التعلم بطيء جدا؟ هل يمكنني إيجاد طريقة لتجنب هذه المشكلة؟

لفهم مصدر المشكلة ، نذكر أن الخلايا العصبية لدينا تتعلم من خلال التغييرات في الوزن والإزاحة بمعدل تحدده المشتقات الجزئية لوظيفة التكلفة ، ∂C / ∂w و ∂C / ∂b. إن قول "التعلم بطيء" هو نفس القول بأن هذه المشتقات الجزئية صغيرة. المشكلة هي أن نفهم لماذا هم صغيرون. للقيام بذلك ، دعونا نحسب المشتقات الجزئية. تذكر أننا نستخدم دالة التكلفة التربيعية ، والتي تعطى بالمعادلة (6):

$$

$$C = \ frac {(y-a) ^ 2} {2} \ tag {54}$$

حيث a هو خرج الخلايا العصبية عندما يتم استخدام x = 1 عند الإدخال ، و y = 0 هي المخرجات المطلوبة. لكتابة هذا مباشرة من خلال الوزن والإزاحة ، تذكر أن a = σ (z) ، حيث z = wx + b. باستخدام قاعدة السلسلة للتمايز حسب الوزن والتشريد ، نحصل على:

$$

$$\ frac {\ جزئية C} {\ جزئية w} = (a-y) \ sigma '(z) x = a \ sigma' (z) \ tag {55}$$

$$

$$\ frac {\ جزئية C} {\ جزئية b} = (a-y) \ sigma '(z) = a \ sigma' (z) \ tag {56}$$

حيث استبدلت x = 1 و y = 0. لفهم سلوك هذه التعبيرات ، دعونا نلقي نظرة فاحصة على المصطلح σ '(z) على اليمين. أذكر شكل السيني:



يوضح الرسم البياني أنه عندما يكون ناتج الخلايا العصبية قريبًا من 1 ، يصبح المنحنى مسطحًا للغاية ، ويصبح σ '(z) صغيرًا. تخبرنا المعادلتان (55) و (56) أن ∂C / ∂w و ∂C / ∂b تصبحا صغيرين للغاية. ومن هنا التباطؤ في التعلم. علاوة على ذلك ، كما سنرى لاحقًا ، يحدث تباطؤ التدريب ، في الواقع ، لنفس السبب وفي الجمعية الوطنية ذات الطابع الأكثر عمومية ، وليس فقط في أبسط مثال لدينا.

تقديم وظيفة التكلفة عبر الانتروبيا

ماذا نفعل مع إبطاء التعلم؟ اتضح أنه يمكننا حل المشكلة عن طريق استبدال الوظيفة التربيعية للقيمة بوظيفة أخرى ذات قيمة ، تعرف باسم إنتروبيا. لفهم إنتروبيا ، نبتعد عن أبسط نموذج لدينا. لنفترض أننا ندرب خلية عصبية تحتوي على عدة قيم إدخال × ₁ و x ₂ و ... الأوزان المقابلة w ₁ و w ₂ و ... والإزاحة b:



وبطبيعة الحال ، سيكون ناتج الخلايا العصبية a = σ (z) ، حيث z = ∑ _j w _j x _j + b هو مجموع العناصر المرجحة. نحدد وظيفة تكلفة الانتروبيا لخلية عصبية معينة

$$

$$C = - \ frac {1} {n} \ sum_x \ left [y \ ln a + (1-y) \ ln (1-a) \ right] \ tag {57}$$

حيث n هو العدد الإجمالي لوحدات بيانات التدريب ، يذهب المجموع إلى جميع بيانات التدريب x ، و y هو الناتج المرغوب المقابل.

ليس من الواضح أن المعادلة (57) تحل مشكلة إبطاء التعلم. بصراحة ، ليس من الواضح أنه من المنطقي أن نسميها دالة ذات قيمة! قبل أن نتحول إلى التباطؤ في التعلم ، دعونا نرى بأي معنى يمكن تفسير الإنتروبيا على أنها دالة ذات قيمة.

تجعل خاصيتان بشكل خاص من المعقول تفسير إنتروبيا على أنها دالة ذات قيمة. أولاً ، أكبر من الصفر ، وهذا هو ، C> 0. وللاحظ ذلك ، لاحظ أن (أ) جميع أعضاء المجموع في (57) سلبيون ، لأن كلا اللوغاريتمات مأخوذة من أرقام في النطاق من 0 إلى 1 ، و (ب) علامة الطرح أمام المجموع.

ثانياً ، إذا كان الناتج الحقيقي للخلية العصبية قريبًا من المخرجات المرغوبة لجميع مدخلات التدريب x ، فسيكون الانتروبيا المتقارب قريبًا من الصفر. لإثبات ذلك ، سنحتاج إلى افتراض أن المخرجات المطلوبة y ستكون إما 0 أو 1. عادةً ما يحدث هذا عند حل مشاكل التصنيف ، أو حساب وظائف Boolean. لفهم ما يحدث إذا لم تقم بهذا الافتراض ، ارجع إلى التدريبات في نهاية القسم.

لإثبات ذلك ، تخيل أن y = 0 و a≈0 بالنسبة لبعض المدخلات x. لذلك سيكون عندما يعالج العصبون مثل هذا الإدخال جيدًا. نرى أن المصطلح الأول من التعبير (57) للقيمة يختفي ، لأن y = 0 ، والثاني هو −ln (1 - a) ≈0. وينطبق الشيء نفسه عندما y = 1 و a≈1. لذلك ، ستكون مساهمة القيمة صغيرة إذا كان الناتج الحقيقي قريبًا من المستوى المطلوب.

بإيجاز ، نجد أن الانتروبيا المتقاطعة إيجابية ، وتميل إلى الصفر عندما تحسب الخلية العصبية المخرجات المطلوبة y بشكل أفضل لجميع مدخلات التدريب x. نتوقع وجود كل من الخصائص في دالة التكلفة. والواقع أن كلا من هذه الخصائص تتحقق بالقيمة التربيعية. لذلك ، عبر إنتروبيا هو خبر جيد. ومع ذلك ، فإن وظيفة التكلفة بين الإنتروبيا لها ميزة لأنها ، على عكس القيمة التربيعية ، تتجنب مشكلة إبطاء التعلم. لرؤية هذا ، دعونا نحسب المشتق الجزئي للقيمة مع إنتروبيا بالوزن. استبدل a = σ (z) في (57) ، طبّق قاعدة السلسلة مرتين ، واحصل عليها

$$

$$\ frac {\ جزئية C} {\ جزئية w_j} = - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ frac {\ جزئي \ sigma} {\ جزئية w_j} \ العلامة {58}$$

$$

$$= - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ sigma '(z) x_j \ tag {59}$$

بالتحول إلى قاسم مشترك وتبسيط ، نحصل على:

$$

$$\ frac {\ جزئية C} {\ جزئية w_j} = \ frac {1} {n} \ sum_x \ frac {\ sigma '(z) x_j} {\ sigma (z) (1- \ sigma (z)) } (\ سيجما (ض) - ص). \ العلامة {60}$$

باستخدام تعريف السيني ، σ (z) = 1 / (1 + e ^−z ) وقليلًا من الجبر ، يمكننا أن نظهر أن σ ′ (z) = σ (z) (1 - σ (z)). سأطلب منك التحقق من ذلك في التمرين أكثر ، لكن الآن ، أقبله كحقيقة. تم إلغاء المصطلحات σ (z) و σ (z) (1 - σ (z)) ، وهذا يؤدي إلى

$$

$$\ frac {\ جزئية C} {\ جزئية w_j} = \ frac {1} {n} \ sum_x x_j (\ sigma (z) -y). \ العلامة {61}$$

تعبير عظيم. ويترتب على ذلك أن السرعة التي يتم بها تدريب الأوزان يتم التحكم فيها بواسطة σ (z) ،y ، أي عن طريق الخطأ في الإخراج. كلما كان الخطأ أكبر ، كلما تعلمت الخلايا العصبية بشكل أسرع. هذا يمكن توقعه بشكل حدسي. يتجنب هذا الخيار التباطؤ في التعلم الناتج عن المصطلح "(" (z) في معادلة تكلفة تربيعية مماثلة (55). عندما نستخدم الانتروبيا المتقاطعة ، فإن المصطلح σ '(z) يتم تقليله ولم يعد لدينا ما يدعو للقلق بشأن صغر حجمه. هذا التخفيض هو معجزة خاصة مضمونة من خلال وظيفة التكلفة عبر الانتروبيا. في الواقع ، بالطبع ، هذه ليست معجزة. كما سنرى لاحقًا ، تم اختيار إنتروبيا على وجه التحديد لهذه الخاصية.

وبالمثل ، يمكن حساب المشتق الجزئي للتحيز. لن أعطي كل التفاصيل مرة أخرى ، لكن يمكنك التحقق من ذلك بسهولة

$$

$$\ frac {\ جزئية C} {\ جزئية b} = \ frac {1} {n} \ sum_x (\ sigma (z) -y). \ العلامة {62}$$

يساعد هذا مرة أخرى في تجنب تعلم التخلف بسبب المصطلح "(" (z) في معادلة مماثلة للقيمة التربيعية (56).

ممارسة

• تحقق من أن σ ′ (z) = σ (z) (1 - σ (z)).

دعنا نعود إلى مثالنا بعيد المنال الذي لعبناه به سابقًا ونرى ما سيحدث إذا استخدمنا إنتروبيا بدلاً من القيمة التربيعية. للتوليف ، نبدأ بالحالة التي عملت فيها التكلفة التربيعية بشكل مثالي عندما كان الوزن الأولي 0.6 وكان الإزاحة 0.9. تحتوي المقالة الأصلية على نموذج تفاعلي يمكنك من خلاله النقر فوق الزر "تشغيل" ومعرفة ما يحدث عند استبدال القيمة التربيعية بعلم إنتروبيا.

ليس من المستغرب أن يتم تدريب الخلايا العصبية في هذه الحالة تمامًا كما كان من قبل. الآن دعونا نلقي نظرة على الحالة التي اعتُبرت فيها العصبونات ، حيث يبدأ الوزن والازاحة في 2.0.



النجاح! هذه المرة ، تعلمت العصبونات بسرعة ، كما أردنا. إذا نظرت عن كثب ، يمكنك أن ترى أن ميل منحنى التكلفة أكثر حدة مبدئيًا مقارنة بالمنطقة المسطحة لمنحنى القيمة التربيعية المقابلة. تمنحنا هذه إنتروبيا عبر البلاد هذا الهدوء ، ولا تسمح لنا بالتعطل حيث نتوقع أسرع تدريب للخلية العصبية عندما تبدأ بأخطاء كبيرة.

لم أقل سرعة التدريب المستخدمة في الأمثلة الأخيرة. في وقت سابق ، مع قيمة التربيعية ، استخدمنا η = 0.15. يجب أن نستخدم نفس السرعة في الأمثلة الجديدة؟ في الواقع ، عند تغيير دالة التكلفة ، من المستحيل أن نقول بالضبط ما يعنيه استخدام السرعة "ذاتها" للتعلم ؛ سيكون مقارنة بين التفاح والبرتقال. بالنسبة لكلتا الدالتين من حيث التكلفة ، جربت البحث عن سرعة تعلم تتيح لي رؤية ما يحدث. إذا كنت لا تزال مهتمًا ، فأحدث الأمثلة ، 0.00 = 0.005.

يمكنك القول أن تغيير سرعة التعلم يجعل الرسومات بلا معنى. من يهتم بسرعة تعلم الخلايا العصبية إذا كان بإمكاننا اختيار سرعة التعلم بشكل تعسفي؟ لكن هذا الاعتراض لا يأخذ في الاعتبار النقطة الرئيسية. ليس معنى الرسوم البيانية في السرعة المطلقة للتعلم ، ولكن في كيفية تغير هذه السرعة. عند استخدام الوظيفة التربيعية ، يكون التدريب أبطأ إذا كانت الخلية العصبية خاطئة للغاية ، ثم تسير بشكل أسرع عندما تقترب العصبون من الإجابة المطلوبة. مع الانتروبيا ، يكون التعلم أسرع عندما ترتكب الخلية العصبية خطأ كبيرا. وهذه العبارات لا تعتمد على سرعة تعلم معينة.

درسنا عبر إنتروبيا لعصب واحد. ومع ذلك ، فمن السهل التعميم على الشبكات ذات الطبقات العديدة والعديد من الخلايا العصبية. لنفترض أن y = y ₁ ، y ₂ ، ... هي القيم المرغوبة للخلايا العصبية الخرجية ، أي أن الخلايا العصبية في الطبقة الأخيرة ، و ^L ₁ ، ^L ₂ ، ... هي قيم الخرج ذاتها. ثم يمكن تحديد إنتروبيا على النحو التالي:

$$

$$C = - \ frac {1} {n} \ sum_x \ sum_j \ left [y_j \ ln a ^ L_j + (1-y_j) \ ln (1-a ^ L_j) \ right] \ tag {63}$$

هذا هو نفس المعادلة (57) ، فقط الآن لدينا مجموعتنا على جميع الخلايا العصبية الناتجة. لن أقوم بتحليل المشتق بالتفصيل ، لكن من المعقول أن نفترض أنه باستخدام التعبير (63) يمكننا تجنب التباطؤ في الشبكات التي تحتوي على العديد من الخلايا العصبية. إذا كنت مهتمًا ، يمكنك أن تأخذ المشتق في المشكلة أدناه.

بالمناسبة ، فإن مصطلح "cross entropy" أستخدمه يخلط بين بعض القراء الأوائل للكتاب لأنه يتناقض مع مصادر أخرى. على وجه الخصوص ، في كثير من الأحيان يتم تحديد إنتروبيا عبر توزيعات الاحتمال ، pj
و qj ، مثل ∑ _j p _j lnq _j . يمكن أن يرتبط هذا التعريف بـ (57) ، إذا اعتبرت إحدى الخلايا العصبية السينيّة إعطاء توزيع احتمالي يتكون من تنشيط الخلايا العصبية a و 1 - قيمة مكملة له.

ومع ذلك ، إذا كان لدينا العديد من الخلايا العصبية السيني في الطبقة الأخيرة ، فإن المتجه a ^L _j عادة لا يعطي توزيع احتمالي. ونتيجة لذلك ، فإن تعريف النوع ∑ _j p _j lnq _j لا معنى له ، لأننا لا نعمل مع توزيعات الاحتمال. بدلاً من ذلك (63) ، يمكن للمرء أن يتخيل كيف يتم تلخيص مجموعة موجزة من الإنتروبيا لكل خلية عصبية ، حيث يتم تفسير تنشيط كل خلية عصبية كجزء من توزيع الاحتمال المكون من عنصرين (بالطبع ، لا توجد عناصر احتمالية في شبكاتنا ، وبالتالي فهي في الواقع ليست احتمالات). في هذا المعنى ، (63) سيكون تعميم إنتروبيا عبر توزيعات الاحتمالات.

متى يجب استخدام إنتروبيا بدلاً من القيمة التربيعية؟ في الواقع ، سيتم استخدام إنتروبيا بشكل دائم تقريبًا بشكل أفضل إذا كان لديك خلايا عصبية ناتجة عن السيني. لفهم ذلك ، تذكر أنه عند إعداد شبكة ، عادة ما نقوم بتهيئة الأوزان والإزاحة باستخدام عملية عشوائية. قد يحدث أن يؤدي هذا الاختيار إلى حقيقة أن الشبكة سوف تسيء تفسير بعض بيانات إدخال التدريب تمامًا - على سبيل المثال ، تميل الخلية العصبية إلى 1 ، عندما يجب أن تذهب إلى 0 ، أو العكس. إذا استخدمنا قيمة من الدرجة الثانية تؤدي إلى إبطاء التدريب ، فلن يتوقف التدريب على الإطلاق ، حيث إن الأوزان ستستمر في التدريب على أمثلة تدريب أخرى ، لكن هذا الموقف غير مرغوب فيه بشكل واضح.

تمارين

• واحدة من الصيد عبر إنتروبيا هو أنه في البداية يمكن أن يكون من الصعب تذكر الأدوار المقابلة من y و a. من السهل الخلط ، لأنه سيكون صحيحًا ، - [ylna + (1 - y) ln (1 - a)] أو - [alny + (1 - a) ln (1 - y)]. ماذا سيحدث للتعبير الثاني عندما تكون y = 0 أو 1؟ هل تؤثر هذه المشكلة على التعبير الأول؟ لماذا؟
• في مناقشة خلية عصبية واحدة في بداية القسم ، قلت إن إنتروبيا صغيرة إذا كانت small (z) fory لجميع بيانات إدخال التدريب. , y 0 1. , (, ) y 0 1. , , σ(z)=y . ,

  $$

  $$C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)] \tag{64}$$
  . −[ylny+(1−y)ln(1−y)] .

• . ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j) \tag{65}$$
  σ'(z ^L _j ) , . , δ ^L x

  $$

  $$\delta^L = a^L-y \tag{66}$$
  , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{67}$$
  σ'(z ^L _j ) , , , . . , .
• . , . , , , , a ^L _j = z ^L _j . , δL x

  $$

  $$\delta^L = a^L-y \tag{68}$$
  , , , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}$$

  $$

  $$\frac{\partial C}{\partial b^L_{j}} = \frac{1}{n} \sum_x (a^L_j-y_j) \tag{70}$$
  , , . .

MNIST

من السهل تطبيق Cross entropy كجزء من برنامج يعلم الشبكة باستخدام النسب المتدرج وانتشار الظهر. سنفعل ذلك لاحقًا من خلال تطوير نسخة محسّنة من برنامج التصنيف الرقمي المكتوب بخط اليد في وقت مبكر من MNIST، network.py. يُسمى البرنامج الجديد network2.py ، ولا يشمل إنتروبيا فقط ، ولكن أيضًا العديد من التقنيات الأخرى التي تم تطويرها في هذا الفصل. في غضون ذلك ، دعونا نرى مدى تصنيف برنامجنا الجديد لأرقام MNIST. كما في الفصل 1 ، سوف نستخدم شبكة تضم 30 خلية عصبية مخفية ، وحزمة صغيرة بحجم 10. سنضبط سرعة التعلم η = 0.5 وسنتعلم 30 عصور.

كما قلت من قبل ، من المستحيل تحديد بالضبط سرعة التدريب المناسبة في هذه الحالة ، لذلك جربت الاختيار. صحيح ، هناك طريقة لربط معدل التعلم بشكل استكشافي تقريبًا لعبور القيمة التربيعية والتربيعية. لقد رأينا سابقًا أنه من حيث التدرج اللوني للقيمة التربيعية ، هناك مصطلح إضافي σ '= σ (1-σ). افترض أننا متوسط ​​هذه القيم ل for ، ∫ ¹ ₀ dσ σ (1 - σ) = 1/6. يمكن ملاحظة أن التكلفة التربيعية (تقريبًا جدًا) في المتوسط ​​تتعلم بمعدل 6 مرات أبطأ بنفس معدل التعلم. يشير هذا إلى أن نقطة الانطلاق الجيدة ستكون تقسيم سرعة التعلم لوظيفة تربيعية على 6. بالطبع ، هذه ليست حجة صارمة على الإطلاق ، ويجب ألا تأخذها على محمل الجد. لكن يمكن أن يكون مفيدًا في بعض الأحيان كنقطة انطلاق.

تختلف واجهة network2.py اختلافًا طفيفًا عن network.py ، لكن لا يزال يجب أن يكون واضحًا ما يحدث. يمكن الحصول على الوثائق على network2.py باستخدام أمر المساعدة (network2.Network.SGD) في shell python.

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True) 

لاحظ ، بالمناسبة ، أن الأمر net.large_weight_initializer () يستخدم لتهيئة الأوزان والإزاحة بالطريقة نفسها الموصوفة في الفصل 1. نحتاج إلى تشغيله لأننا سنغير تهيئة الأوزان بشكل افتراضي لاحقًا. نتيجة لذلك ، بعد بدء جميع الأوامر المذكورة أعلاه ، نحصل على شبكة تعمل بدقة 95.49 ٪. هذا قريب جدًا من نتيجة الفصل الأول ، 95.42٪ ، باستخدام القيمة التربيعية.

لنلقِ نظرة أيضًا على الحالة التي نستخدم فيها 100 خلية عصبية خفية ونعبر عن إنتروب ، ونترك الباقي كما هو. في هذه الحالة ، تبلغ الدقة 96.82٪. هذا تحسن كبير على نتائج الفصل الأول ، حيث حققنا دقة 96.59 ٪ باستخدام القيمة التربيعية. قد يبدو التغيير بسيطًا ، لكن أعتقد أن الخطأ انخفض من 3.41٪ إلى 3.18٪. وهذا هو ، لقد تخلصنا من أخطاء 1/14 تقريبًا. هذا جيد جدا

من الجميل أن تعطينا دالة التكلفة عبر الانتروبيا نتائج متشابهة أو أفضل مقارنة بالقيمة التربيعية. ومع ذلك ، فإنها لا تثبت بشكل قاطع أن الانتروبيا المتقاطعة هي الخيار الأفضل. الحقيقة هي أنني لم أحاول اختيار المعلمات الفائقة على الإطلاق - سرعة التدريب ، وحجم الحزمة المصغرة ، إلخ. لجعل التحسين أكثر إقناعًا ، نحتاج إلى معالجة تحسينهم بشكل صحيح. لكن النتائج لا تزال ملهمة ، وتؤكد حساباتنا النظرية أن الانتروبيا المتقاطعة هي خيار أفضل من دالة التكلفة التربيعية.

في هذا السياق ، سوف يمر هذا الفصل بأكمله ، ومن حيث المبدأ ، بقية الكتاب. سنطور تقنية جديدة ونختبرها ونحصل على "نتائج محسنة". بالطبع ، من الجيد أن نرى هذه التحسينات. لكن تفسيرها صعب دائمًا. سيكون مقنعًا فقط إذا رأينا تحسينات بعد العمل الجاد على تحسين جميع المعلمات الفائقة الأخرى. وهذه مهمة معقدة إلى حد ما ، تتطلب موارد حسابية كبيرة ، وعادة لن نتعامل مع مثل هذا التحقيق الشامل. بدلاً من ذلك ، سنذهب أبعد من ذلك على أساس اختبارات غير رسمية ، مثل تلك المذكورة أعلاه. لكن عليك أن تضع في اعتبارك أن مثل هذه الاختبارات ليست دليلًا لا لبس فيه ، وأن تراقب هذه الحالات بعناية عندما تبدأ الحجج في الفشل.

حتى الآن ، نناقش إنتروبيا بالتفصيل. لماذا تضيع الكثير من الجهد إذا كان هذا يعطي تحسنا طفيفا في نتائج MNIST لدينا؟ في وقت لاحق من هذا الفصل ، سنرى تقنيات أخرى - على وجه الخصوص ، التنظيم - والتي تقدم تحسينات أقوى بكثير. فلماذا نركز على الانتروبيا؟ على وجه الخصوص ، لأن الانتروبيا هي وظيفة ذات قيمة شائعة الاستخدام ، لذلك فهي تستحق الفهم الجيد. ولكن السبب الأكثر أهمية هو أن تشبع الخلايا العصبية هو مشكلة مهمة في مجال الشبكات العصبية ، والتي سنعود إليها باستمرار في جميع أنحاء الكتاب. لذلك ، ناقشت الانتروبيا عبر مثل هذه التفاصيل ، لأنه مختبر جيد للبدء في فهم تشبع الخلايا العصبية وكيفية التعامل مع النهج لهذه المشكلة.

ماذا يعني الانتروبيا؟ من أين تأتي؟

تدور مناقشتنا حول الانتروبيا حول التحليل الجبري والتطبيق العملي. هذا مفيد ، لكن نتيجة لذلك ، تظل الأسئلة المفاهيمية الأوسع دون إجابة ، على سبيل المثال: ماذا يعني الانتروبيا؟ هل هناك طريقة بديهية لتقديمها؟ كيف يمكن للناس حتى الخروج مع إنتروبيا؟

لنبدأ بالأخير: ما الذي يمكن أن يجعلنا نفكر في إنتروبيا؟ لنفترض أننا اكتشفنا تباطؤًا في التعلم تم وصفه مسبقًا وأدركنا أنه ناجم عن المصطلحين σ '(z) في المعادلتين (55) و (56). بعد إلقاء نظرة سريعة على هذه المعادلات ، يمكننا التفكير فيما إذا كان من الممكن اختيار دالة التكلفة هذه بحيث يختفي المصطلح "σ" (z). ثم التكلفة C = C _x مثال تدريب واحد _من شأنه تلبية المعادلات:

$$

$$\ frac {\ جزئية C} {\ جزئية w_j} = x_j (a-y) \ tag {71}$$

$$

$$\ frac {\ جزئية C} {\ جزئية b} = (a-y) \ tag {72}$$

إذا اخترنا دالة قيمة تجعلها صحيحة ، فعندئذ يفضلون ببساطة فهم الفهم البديهي أنه كلما زاد الخطأ الأولي ، كلما تعلم الخلايا العصبية أسرع. كما أنهم سيصلحون مشكلة التباطؤ. في الواقع ، بدءًا من هذه المعادلات ، نبيّن أنه من الممكن اشتقاق شكل إنتروبيا من خلال اتباع غريزة رياضية ببساطة. لرؤية هذا ، نلاحظ أنه بناءً على قاعدة السلسلة ، نحصل على:

$$

$$\ frac {\ جزئية C} {\ جزئية b} = \ frac {\ جزئية C} {\ جزئية a} \ sigma '(z) \ tag {73}$$

باستخدام في المعادلة الأخيرة σ ′ (z) = σ (z) (1 - σ (z)) = a (1 - a) ، نحصل على:

$$

$$\ frac {\ جزئية C} {\ جزئية b} = \ frac {\ جزئية C} {\ جزئية a} a (1-a) \ tag {74}$$

مقارنة مع المعادلة (72) ، نحصل على:

$$

$$\ frac {\ جزئية C} {\ جزئية a} = \ frac {a-y} {a (1-a)} \ tag {75}$$

دمج هذا التعبير على ، نحصل على:

$$

$$C = - [y \ ln a + (1-y) \ ln (1-a)] + {\ rm ثابت} \ العلامة {76}$$

هذه هي مساهمة مثال تدريب منفصل x في دالة التكلفة. للحصول على وظيفة التكلفة الكاملة ، نحتاج إلى تقييم جميع أمثلة التدريب ، ونصل إلى:

$$

$$C = - \ frac {1} {n} \ sum_x [y \ ln a + (1-y) \ ln (1-a)] + {\ rm ثابت} \ العلامة {77}$$

الثابت هنا هو متوسط ​​الثوابت الفردية لكل من أمثلة التدريب. كما ترون ، تحدد المعادلتان (71) و (72) بشكل فريد شكل الانتروبيا المتداخلة ، واللحام في ثابت مشترك. لم يتم إخراج إنتروبيا عبر الهواء بطريقة سحرية. يمكن العثور عليها بطريقة بسيطة وطبيعية.

ماذا عن الفكرة البديهية لعبر الكون؟ كيف نتخيل ذلك؟ شرح مفصل من شأنه أن يقودنا إلى تجاوز الدورة التدريبية لدينا. ومع ذلك ، يمكننا أن نذكر وجود طريقة قياسية لتفسير الانتروبيا ، والتي تنشأ من مجال نظرية المعلومات. تحدث تقريبًا ، عبر إنتروبيا هو مقياس للدهشة. على سبيل المثال ، تحاول الخلايا العصبية لدينا حساب الوظيفة x → y = y (x). ولكن بدلاً من ذلك ، تحسب الدالة x → a = a (x). لنفترض أننا نتخيل كتقدير للخلايا العصبية لاحتمال أن y = 1 ، و 1-a هو احتمال أن القيمة الصحيحة لـ y تساوي 0. ثم يقيس الانتروبيا مقدار ما "نفاجأ به" ، في المتوسط ​​، عندما العثور على القيمة الحقيقية لل y. نحن لسنا متفاجئين إذا كنا نتوقع مخرجًا ، ونحن مندهشون جدًا إذا كان المخرج غير متوقع. بالطبع ، لم أقدم تعريفًا صارمًا لـ "المفاجأة" ، لذلك كل هذا يمكن أن يبدو كأنه خرف فارغ. ولكن في الواقع ، في نظرية المعلومات هناك طريقة دقيقة لتحديد غير متوقع. لسوء الحظ ، لست على دراية بأي أمثلة لمناقشات جيدة وقصيرة ومكتفية ذاتياً حول هذه النقطة على الإنترنت. ولكن إذا كنت مهتمًا بالحفر بشكل أعمق ، فإن مقالة Wikipedia تحتوي على معلومات عامة جيدة سترسل لك في الاتجاه الصحيح. يمكن الاطلاع على التفاصيل في الفصل 5 حول عدم المساواة في كرافت في كتاب عن نظرية المعلومات .

مهمة

• لقد ناقشنا بالتفصيل التباطؤ في التعلم الذي يمكن أن يحدث عندما يتم تشبع الخلايا العصبية في الشبكات التي تستخدم دالة التكلفة التربيعية في التعلم. هناك عامل آخر يمكن أن يمنع التعلم هو وجود المصطلح x _j في المعادلة (61). بسبب ذلك ، عندما يقترب الناتج x _{j من} الصفر ، سيتم تدريب الوزن المقابل w _j ببطء. وضح سبب استحالة إزالة المصطلح x _j باختيار وظيفة تكلفة مبدعة.

Softmax (وظيفة الحد الأقصى لينة)

في هذا الفصل ، سوف نستخدم في الغالب دالة التكلفة عبر الانتروبيا لحل مشاكل إبطاء التعلم. ومع ذلك ، أود أن أناقش بإيجاز طريقة أخرى لهذه المشكلة ، بناءً على ما يسمى softmax طبقات من الخلايا العصبية. لن نستخدم طبقات Softmax للفترة المتبقية من هذا الفصل ، لذلك إذا كنت في عجلة من أمرك ، فيمكنك تخطي هذا القسم. ومع ذلك ، لا يزال Softmax يستحق الفهم ، خاصة لأنه مثير للاهتمام في حد ذاته ، ولا سيما لأننا سنستخدم طبقات Softmax في الفصل 6 ، في مناقشتنا للشبكات العصبية العميقة.

فكرة Softmax هي تحديد نوع جديد من طبقة الإخراج لـ HC. يبدأ بنفس طريقة الطبقة السيني ، بتكوين مدخلات مرجحة $$$z ^ L_j = \ sum_ {k} w ^ L_ {jk} a ^ {L-1} _k + b ^ L_j$ . ومع ذلك ، نحن لا نستخدم السيني للحصول على إجابة. في طبقة Softmax ، نطبق وظيفة Softmax على z ^L _j . ووفقًا لها ، فإن تنشيط ^{L L} _للخلية العصبية رقم j يساوي:

$$

$$a ^ L_j = \ frac {e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} \ tag {78}$$

حيث في المقام نجمع كل الخلايا العصبية الناتجة.

إذا كانت وظيفة Softmax غير مألوفة لك ، فستبدو المعادلة (78) غامضة بالنسبة لك. ليس من الواضح على الإطلاق لماذا يجب علينا استخدام هذه الوظيفة. كما أنه ليس من الواضح أنه سيساعدنا في حل مشكلة إبطاء التعلم. لفهم المعادلة (78) بشكل أفضل ، افترض أن لدينا شبكة بها أربع خلايا عصبية مخرجات وأربعة مدخلات مرجحة مقابلة ، والتي سنقوم بتعيينها على أنها ^{L L} و z ^L ₂ و z ^L ₃ و z ^L ₄ . تحتوي المقالة الأصلية على منزلقات ضبط تفاعلية ، والتي يتم تعيين القيم المحتملة للمدخلات المرجحة والجدول الزمني لتنشيط الخرج المقابل. تتمثل نقطة الانطلاق الجيدة لدراستها في استخدام شريط التمرير السفلي لزيادة z ^L ₄ .





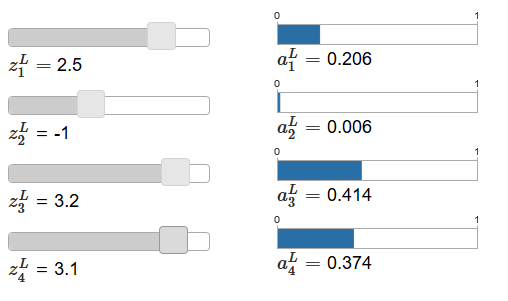
بزيادة z ^L ₄ ، يمكن للمرء أن يلاحظ زيادة في تنشيط الخرج المقابل ، ^L ₄ ، وانخفاض في تنشيطات الخرج الأخرى. مع تقليل z ^L ₄ ، سينخفض ^L ₄ ، وستزداد جميع تنشيطات الخرج الأخرى. بعد النظر عن كثب ، سترى في كلتا الحالتين أن التغيير العام في التنشيطات الأخرى يعوض تمامًا التغيير الذي يحدث في ^L ₄ . والسبب في ذلك هو ضمان أن جميع تنشيطات الخرج في المجموع تعطي 1 ، والتي يمكننا إثباتها باستخدام المعادلة (78) وبعض الجبر:

$$

$$\ sum_j a ^ L_j = \ frac {\ sum_j e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} = 1 \ tag {79}$$

نتيجة لذلك ، مع زيادة ^L _{4 ،} يجب أن تنخفض تنشيطات الخرج المتبقية بنفس القيمة في المجموع لضمان أن يكون مجموع كل تنشيطات المخرجات مساويًا 1. وبالطبع ، ستكون عبارات مماثلة صحيحة لجميع عمليات التنشيط الأخرى.

ويستنتج أيضًا من المعادلة (78) أن جميع عمليات تنشيط الخرج إيجابية ، لأن الدالة الأسية إيجابية. عند دمج هذا مع الملاحظة من القسم السابق ، نجد أن إخراج طبقة Softmax عبارة عن مجموعة من الأرقام الموجبة تعطي إجماليًا 1. بمعنى آخر ، يمكن تمثيل إخراج طبقة Softmax كتوزيع احتمالي.

حقيقة أن إخراج طبقة Softmax هو توزيع الاحتمالات لطيف للغاية. في العديد من المشكلات ، يكون من المناسب أن تكون قادرًا على تفسير تنشيطات الخرج a ^L _j كتقدير من قبل الشبكة لاحتمال أن يكون bulet j هو الخيار الصحيح. لذلك ، على سبيل المثال ، في مشكلة التصنيف MNIST ، يمكننا تفسير ^L _j كتقدير من قبل الشبكة لاحتمال أن j سيكون الإصدار الصحيح من تصنيف الرقم.

على العكس من ذلك ، إذا كانت طبقة المخرجات كانت عبارة عن sigmoid ، فلا يمكننا بالتأكيد افتراض أن عمليات التنشيط تشكل توزيعات احتمالية. لن أثبت ذلك بدقة ، لكن من المعقول أن نفترض أن تنشيط طبقة السيني في الحالة العامة لا يشكل توزيعًا محتملاً. لذلك ، باستخدام طبقة مخرجات السيني ، لن نحصل على مثل هذا التفسير البسيط لتنشيط المخرجات.

ممارسة

• اكتب مثالًا يوضح أنه في شبكة ذات طبقة مخرجات السيني ، لا تضيف تنشيطات الخرج a ^L _j دائمًا ما يصل إلى 1.

نبدأ في فهم بعض الشيء عن وظائف Softmax وكيف تتصرف طبقات Softmax. فقط للتلخيص: يضمن الأسس في المعادلة (78) أن تكون جميع عمليات تنشيط الإخراج إيجابية. يضمن مجموع مقام المعادلة (78) أن Softmax تعطي ما مجموعه 1. لذلك ، لم يعد هذا النوع من المعادلات غامضًا: هذه طريقة طبيعية لضمان أن تكون تنشيطات الخرج بمثابة توزيع احتمالي. يمكن تخيل Softmax كوسيلة لتوسيع نطاق z ^L _j ثم ضغطها معًا لتشكيل توزيع الاحتمالات.

تمارين

• رتابة Softmax. أوضح أن La ^L _j / ∂z ^L _k موجبة إذا كانت j = k و سالبة if j ≠ k. نتيجة لذلك ، هناك ضمان لزيادة في z ^L _j لزيادة تنشيط الخرج المقابل a ^L _j ، ويقلل من جميع تنشيطات الخرج الأخرى. لقد رأينا هذا بالفعل تجريبياً باستخدام مثال المتزلجون ، لكن هذا الدليل سيكون صارمًا.
• اللامركزية Softmax. هناك ميزة لطيفة لطبقات السيني هي أن الخرج a ^L _j هو دالة المدخلات المرجحة المقابلة ، ^L _j = σ (z ^L _j ). قم بشرح سبب عدم حدوث ذلك مع طبقة Softmax: يعتمد أي تنشيط إخراج a ^L _j على جميع المدخلات الموزونة.

مهمة

• عكس طبقة Softmax. افترض أن لدينا NS مع طبقة Softmax الإخراج والتفعيلات معروفة ^L _j . بيّن أن المدخلات الموزونة المقابلة لها من النموذج z ^L _j = ln a ^L _j + C ، حيث C ثابتة بمعزل عن j.

تعلم مشكلة التباطؤ

لقد أصبحنا بالفعل على دراية طبقات Softmax من الخلايا العصبية. لكن حتى الآن لم نر كيف تسمح لنا طبقات Softmax بحل مشكلة إبطاء التعلم. لفهم ذلك ، دعنا نحدد دالة تكلفة بناءً على "احتمال السجل". سنستخدم x للدلالة على المدخلات التدريبية للشبكة ، و y للإخراج المرغوب المطلوب. بعد ذلك ، ستكون LPS المرتبطة بهذا الإدخال التدريبي هي:

$$

$$C \ equiv - \ ln a ^ L_y \ tag {80}$$

لذلك ، على سبيل المثال ، إذا درسنا على صور MNIST ، وذهبت الصورة 7 إلى الإدخال ، فسيكون LPS هو ^L ₇ . لفهم هذا بشكل حدسي ، فإننا نعتبر الحالة عندما تتكيف الشبكة جيدًا مع الاعتراف ، أي أنها على يقين من أنها عند الإدخال 7. في هذه الحالة ، ستقوم بتقييم قيمة الاحتمال المطابق ^{لـ L} ₇ على مقربة من 1 ، وبالتالي فإن التكلفة ستكون ^L ₇ صغيرة . على العكس من ذلك ، إذا كانت الشبكة لا تعمل بشكل جيد ، فسيكون احتمال ^L ₇ أقل ، وستكون التكلفة Lln a ^L ₇ أكثر. لذلك ، يتصرف LPS كما هو متوقع من دالة التكلفة.

ماذا عن مشكلة التباطؤ؟ لتحليلها ، نذكر أن الشيء الرئيسي في التباطؤ هو سلوك ∂C / ∂w ^L _jk و /C / ∂b ^L _j . لن أصف بالتفصيل القبض على المشتق - سأطلب منك القيام بذلك في المهام ، لكن باستخدام بعض الجبر يمكنك إظهار ما يلي:

$$

$$\ frac {\ جزئية C} {\ جزئية b ^ L_j} = a ^ L_j-y_j \ tag {81}$$

$$

$$\ frac {\ جزئية C} {\ جزئية w ^ L_ {jk}} = a ^ {L-1} _k (a ^ L_j-y_j) \ tag {82}$$

لقد لعبت قليلاً مع التدوين هنا ، وأنا أستخدم كلمة "y" بشكل مختلف قليلاً عن الفقرة الأخيرة. تشير y إلى إخراج الشبكة المرغوب - أي إذا كان الناتج هو "7" ، فكانت المدخلات هي الصورة 7. وفي هذه المعادلات ، تشير y إلى متجه تنشيط الخرج المقابل لـ 7 ، وهو متجه يحتوي على كل الأصفار باستثناء الوحدة في 7 الموقف ال.

هذه المعادلات هي نفس التعبيرات المتشابهة التي حصلنا عليها في تحليل سابق للإنتروبيا المتقاطعة. قارن ، على سبيل المثال ، المعادلتين (82) و (67). هذه هي نفس المعادلة ، على الرغم من أن الأخيرة يتم حسابها على أمثلة التدريب. وكما في الحالة الأولى ، تضمن هذه التعبيرات عدم تباطؤ التعلم. من المفيد أن تتخيل أن طبقة Softmax الناتجة مع LPS تشبه إلى حد بعيد الطبقة ذات الإخراج السيني والتكلفة على أساس إنتروبيا.

بالنظر إلى تشابهها ، ما الذي يجب استخدامه - إخراج السيني والنتروبيا ، أو إخراج Softmax و LPS؟ في الواقع ، في كثير من الحالات كلا النهجين تعمل بشكل جيد. على الرغم من أننا سنستخدم لاحقًا في هذا الفصل طبقة إخراج السيني مع تكلفة تعتمد على إنتروبيا. في وقت لاحق ، في الفصل 6 ، سوف نستخدم أحيانًا مخرجات Softmax و LPS. سبب التغييرات هو جعل بعض الشبكات التالية أكثر تشابهًا مع الشبكات الموجودة في بعض الأوراق البحثية المؤثرة. من وجهة نظر أكثر عمومية ، يجب استخدام Softmax و LPS عندما تحتاج إلى تفسير تنشيطات المخرجات كاحتمالات. هذا ليس ضروريًا دائمًا ، ولكنه قد يكون مفيدًا في مشكلات التصنيف (مثل MNIST) ، والتي تتضمن فصولًا غير متقاطعة.

المهام

• اشتقاق المعادلات (81) و (82).
• من أين يأتي اسم Softmax؟ لنفترض أننا قمنا بتغيير وظيفة Softmax بحيث يتم إعطاء تنشيط الخرج بواسطة المعادلة

  $$

  $$a ^ L_j = \ frac {e ^ {c z ^ L_j}} {\ sum_k e ^ {c z ^ L_k}} \ tag {83}$$
  حيث c ثابت ثابت. لاحظ أن c = 1 يتوافق مع وظيفة Softmax القياسية. لكن باستخدام قيمة مختلفة لـ c ، نحصل على وظيفة أخرى ستظل مماثلة نوعيًا لـ Softmax. أظهر أن تنشيطات الخرج تشكل توزيعا للاحتمال ، كما هو الحال مع Softmax العادي. لنفترض أننا نجعل c كبيرًا جدًا ، وهذا يعني ، c → & inf ؛. ما هي القيمة المحددة لتفعيلات الخرج a ^L _j ؟ بعد حل هذه المشكلة ، يجب أن يكون من الواضح سبب اعتبار الدالة ذات c = 1 "نسخة مخففة" من الحد الأقصى للوظيفة. هذا هو المكان الذي يأتي منه مصطلح softmax.
• انتشار الظهر مع Softmax و LPS. في الفصل الأخير ، استخلصنا خوارزمية backpropagation لشبكة تحتوي على طبقات السيني. لتطبيق هذه الخوارزمية على طبقات الشبكة و Softmax ، نحتاج إلى اشتقاق التعبير عن الخطأ δ ^L _j ≡ ∂C / ∂z ^L _j . تبين أن التعبير المناسب سيكون

  $$

  $$\ delta ^ L_j = a ^ L_j -y_j \ tag {84}$$
  باستخدام هذا التعبير ، يمكننا تطبيق خوارزمية backpropagation على الشبكة باستخدام طبقة Softmax للإخراج و LPS.

إعادة التدريب والتنظيم

لقد طُلب من الحائز على جائزة نوبل ، إنريكو فيرمي ، أن يكون له رأي في النموذج الرياضي الذي اقترحه عدة زملاء لحل مشكلة جسدية مهمة لم يتم حلها. يتوافق النموذج تمامًا مع التجربة ، لكن فيرمي كان يشك في ذلك. سأل كيف يمكن تغيير العديد من المعلمات في ذلك. "أربعة" ، أخبروه. أجاب فيرمي: "أتذكر كيف أحب صديقي جوني فون نيومان أن يقول أنه مع أربعة معايير يمكنك دفع فيل هناك ، ومع خمسة يمكنك جعله يلوح بجذعته."

معنى التاريخ ، بالطبع ، هو أن النماذج التي تحتوي على عدد كبير من المعلمات المجانية يمكنها وصف مجموعة واسعة من الظواهر بشكل مدهش.حتى لو كان هذا النموذج يعمل بشكل جيد مع البيانات المتاحة ، فإنه لا يجعله تلقائيًا نموذجًا جيدًا. قد يعني هذا فقط أن النموذج لديه حرية كافية لوصف أي مجموعة بيانات بحجم معين تقريبًا دون الكشف عن الفكرة الرئيسية للظاهرة. عندما يحدث هذا ، يعمل النموذج بشكل جيد مع البيانات الموجودة ، لكن لا يمكنه تعميم الموقف الجديد. الاختبار الحقيقي للنموذج هو قدرته على عمل تنبؤات في المواقف التي لم يواجهها من قبل.

كان فيرمي وفون نيومان متشككين في النماذج بأربعة معايير. لدينا NS مع 30 الخلايا العصبية الخفية لتصنيف أرقام MNIST لديها ما يقرب من 24000 المعلمات! هذه بعض المعلمات. لدينا NS مع 100 الخلايا العصبية المخفية لديها ما يقرب من 80،000 المعلمات ، و NS NS العميق العميق من هذه المعلمات في بعض الأحيان الملايين أو حتى المليارات. هل يمكننا الوثوق بنتائج عملهم؟

دعنا نعقد هذه المشكلة عن طريق خلق موقف تؤدي فيه شبكتنا إلى تعميم وضع جديد لها بشكل سيء. سوف نستخدم NS مع 30 من الخلايا العصبية المخفية و 23،860 المعلمات. لكننا لن نقوم بتدريب الشبكة مع جميع الصور 50000 MNIST. بدلاً من ذلك ، نستخدم 1000 فقط. باستخدام مجموعة محدودة سيجعل مشكلة التعميم أكثر وضوحًا. سوف ندرس كما كان من قبل ، باستخدام دالة التكلفة المستندة إلى إنتروبيا ، مع سرعة تعلم تبلغ η = 0.5 وحجم رزمة صغيرة من 10. ومع ذلك ، سوف ندرس 400 عصور ، وهو ما يزيد قليلاً عن ذي قبل ، حيث توجد أمثلة تدريب ليس لدينا الكثير. دعنا نستخدم network2 للنظر في كيفية تغير وظيفة التكلفة:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True, monitor_training_cost=True) 

باستخدام النتائج ، يمكننا إنشاء رسم بياني للتغيرات في التكلفة عند تدريب الشبكة (تم إجراء الرسوم البيانية باستخدام برنامج overfitting.py):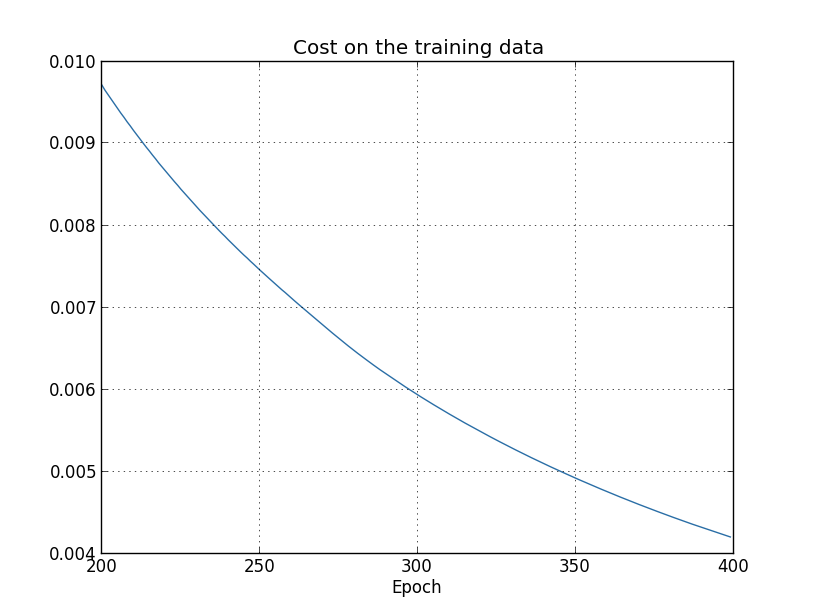



يبدو الأمر مشجعًا ، وهناك انخفاض سلس في التكلفة ، كما هو متوقع. ضع في اعتبارك أنني لم أقم بعرض سوى العصور من 200 إلى 399. ونتيجة لذلك ، نرى على نطاق موسع المراحل المتأخرة من التدريب ، والتي ، كما سنرى لاحقًا ، تحدث كل الأحداث الأكثر إثارة للاهتمام.

الآن ، لنرى كيف تتغير دقة التصنيف في بيانات التحقق بمرور الوقت:



ثم قمت مرة أخرى بزيادة الجدول الزمني. في أول 200 عصر ، غير مرئية هنا ، تزداد الدقة إلى 82٪ تقريبًا. ثم التدريب يبطئ تدريجيا. أخيرًا ، في حوالي 280 عامًا ، لم تتحسن دقة التصنيف. في العصور اللاحقة ، لوحظ تقلبات ستوكاستيك الصغيرة فقط حول قيمة الدقة التي تحققت في عصر 280. قارن هذا بالمخطط السابق ، حيث تنخفض التكلفة المرتبطة ببيانات التدريب بالتدريج. إذا درست هذه التكلفة فقط ، فسيبدو أن النموذج يتحسن. ومع ذلك ، فإن نتائج العمل مع بيانات الاختبار تخبرنا أن هذا التحسين هو مجرد وهم. كما هو الحال في النموذج الذي لم يعجب Fermi به ، لم تعد المعممة التي تدرسها شبكتنا بعد عصر 280 هي بيانات التحقق. لذلك ، هذا التدريب يتوقف عن أن يكون مفيدا. نقول أنه بعد عصر 280 ، إعادة تدريب الشبكة ،أو تجهيزها.

قد تتساءل عما إذا كنت لا أدرس التكلفة بناءً على بيانات التدريب ، وليس مشكلة دقة تصنيف بيانات التحقق. بمعنى آخر ، ربما تكون المشكلة هي أننا نقارن التفاح بالبرتقال. ماذا سيحدث إذا قارنا تكلفة بيانات التدريب بتكلفة التحقق ، أي أننا سنقارن التدابير المماثلة؟ أو ربما يمكننا مقارنة دقة التصنيف لكل من بيانات التدريب والاختبار؟ في الواقع ، تظهر نفس الظاهرة بغض النظر عن كيفية إجراء المقارنة. لكن التفاصيل تتغير. على سبيل المثال ، دعنا نرى قيمة بيانات التحقق:



يمكن ملاحظة أن تكلفة بيانات التحقق تتحسن حتى حوالي القرن الخامس عشر ، ثم تبدأ في التدهور تمامًا ، على الرغم من أن تكلفة بيانات التدريب تستمر في التحسن. هذه علامة أخرى على نموذج تم إعادة تدريبه. ومع ذلك ، فإن السؤال الذي يطرح نفسه ، ما هو عصر يجب أن ننظر في النقطة التي تبدأ إعادة التدريب على الغلبة على التدريب - 15 أو 280؟ من وجهة نظر عملية ، نحن مهتمون مع ذلك بتحسين دقة تصنيف بيانات التحقق ، والتكلفة هي مجرد وسيط لدقة التصنيف. لذلك ، من المنطقي اعتبار عصر 280 نقطة ، وبعدها تبدأ إعادة التدريب في الانتصار على تدريب جمعيتنا الوطنية.

يمكن رؤية علامة أخرى لإعادة التدريب في دقة تصنيف بيانات التدريب:



دقة ينمو ، تصل إلى 100 ٪. وهذا هو ، شبكتنا يصنف بشكل صحيح جميع الصور التدريب 1000! وفي الوقت نفسه ، تزداد دقة التحقق إلى 82.27٪ فقط. أي أن شبكتنا تدرس فقط ميزات مجموعة التدريب ، ولا تتعلم التعرف على الأرقام على الإطلاق. يبدو أن الشبكة تتذكر مجموعة التدريب ببساطة ، ولا تفهم الأرقام جيدًا بما يكفي لتعميمها على مجموعة الاختبار.

إعادة التدريب هي مشكلة خطيرة للجمعية الوطنية. وينطبق هذا بشكل خاص على NSs الحديثة ، والتي عادةً ما تحتوي على كمية كبيرة من الأوزان والتشريد. للحصول على تدريب فعال ، نحتاج إلى طريقة لتحديد وقت حدوث إعادة التدريب حتى لا تتم إعادة التدريب. ونود أيضًا أن نكون قادرين على تقليل آثار إعادة التدريب.

هناك طريقة واضحة للكشف عن إعادة التدريب وهي استخدام النهج أعلاه ، ومراقبة دقة العمل مع بيانات التحقق أثناء التدريب على الشبكة. إذا رأينا أن دقة بيانات التحقق لم تعد تتحسن ، فيجب أن نتوقف عن التدريب. بالطبع ، بالمعنى الدقيق للكلمة ، لن يكون هذا بالضرورة علامة على إعادة التدريب. ربما تتوقف دقة العمل مع بيانات الاختبار والتدريب عن التحسن في نفس الوقت. لكن تطبيق مثل هذه الاستراتيجية سيمنع إعادة التدريب.

وسوف نستخدم مجموعة صغيرة من هذه الاستراتيجية. تذكر أنه عندما نقوم بتحميل البيانات إلى MNIST ، فإننا نقسمها إلى ثلاث مجموعات:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

استخدمنا حتى الآن بيانات التدريب و test_data ، وتجاهلنا validation_data [يؤكد]. يحتوي Validation_data على 10000 صورة ، والتي تختلف عن كل من 50000 صورة لمجموعة التدريب MNIST و 10000 صورة لمجموعة التحقق من الصحة. بدلاً من استخدام test_data لمنع التجاوز ، سنستخدم validation_data. للقيام بذلك ، سوف نستخدم نفس الاستراتيجية تقريبًا الموضحة أعلاه في test_data. بمعنى ، سنقوم بحساب دقة تصنيف validation_data في نهاية كل عصر. بمجرد اكتمال دقة تصنيف validation_data ، سنتوقف عن التعلم. هذه الاستراتيجية تسمى التوقف المبكر. بالطبع ، في الممارسة العملية ، لن نكون قادرين على معرفة فورا أن الدقة مشبعة. بدلاً من ذلك ، سوف نستمر في التدريب حتى نتأكد من ذلك (ونقررعندما تحتاج إلى التوقف ، فليس من السهل دائمًا ، ويمكنك استخدام أساليب أكثر أو أقل عدوانية لهذا الغرض).

لماذا استخدم validation_data لمنع إعادة التدريب بدلاً من test_data؟ يعد استخدام validation_data جزءًا من استراتيجية أكثر عمومية لتقييم الخيارات المختلفة للمعلمات الفائقة - عدد مرات التعلم ، وسرعة التعلم ، وأفضل بنية شبكة ، وما إلى ذلك. نحن نستخدم هذه التقديرات لإيجاد قيم جيدة للمعلمات الفائقة وتعيينها. وعلى الرغم من أنني لم أذكر هذا بعد ، فقد اخترت جزئياً السبب في اختيار المعلمات الفوقية في الأمثلة السابقة في الكتاب.

بالطبع ، لا تجيب هذه الملاحظة على سؤال لماذا نستخدم validation_data ، وليس test_data ، لمنع التجاوز. إنه يحل ببساطة محل الإجابة على سؤال أكثر عمومية - لماذا نستخدم validation_data ، وليس test_data ، لتحديد المعلمات الفوقية؟ لفهم ذلك ، ضع في اعتبارك أنه عند اختيار المعلمات الفائقة ، من المرجح أن نختار من بين مجموعة متنوعة من خياراتها. إذا قمنا بتعيين معلمات تشعبية استنادًا إلى التصنيفات من test_data ، فسنقوم على الأرجح بتخصيص هذه البيانات كثيرًا على وجه التحديد ل test_data. أي أننا قد نعثر على معلمات كبيرة مناسبة لميزات بيانات محددة من test_data ، ومع ذلك ، لن يتم تعميم تشغيل شبكتنا على مجموعات البيانات الأخرى. نحن نتجنب هذا من خلال تحديد المعلمات الفوقية باستخدام validation_data. وبعد ذلك ، بعد تلقي GP نحتاج ،نجري تقييمًا نهائيًا للدقة باستخدام test_data. هذا يعطينا الثقة في أن نتائجنا مع test_data هي مقياس حقيقي لدرجة تعميم NS. بمعنى آخر ، البيانات الداعمة هي بيانات تدريب خاصة تساعدنا على تعلم GP جيد. أحيانًا ما يطلق على هذا النهج لتحديد موقع GPS طريقة الاحتفاظ ، حيث يتم التحقق من صحة validation_data بشكل منفصل عن بيانات التدريب.

في الممارسة العملية ، حتى بعد تقييم جودة العمل على test_data ، سنود تغيير رأينا وتجربة نهج مختلف - ربما بنية شبكة مختلفة - والتي ستتضمن البحث عن مجموعة جديدة من GPs. في هذه الحالة ، هل هناك خطر من أننا سوف نتكيف دون داع مع test_data؟ هل سنحتاج إلى عدد لا حصر له من مجموعات البيانات بحيث يمكننا التأكد من أن نتائجنا معممة جيدًا؟ بشكل عام ، هذه مشكلة عميقة ومعقدة. ولكن لأغراضنا العملية ، لن نقلق كثيرًا بشأن هذا. نحن ببساطة نتعمق في إجراء مزيد من البحوث باستخدام طريقة بسيطة للاحتفاظ تعتمد على بيانات التدريب ، validation_data و test_data ، كما هو موضح أعلاه.

حتى الآن ، نحن نفكر في إعادة التدريب باستخدام 1000 صورة تدريبية. ماذا يحدث إذا استخدمنا مجموعة تدريب كاملة من 50000 صورة؟ سنترك جميع المعلمات الأخرى بدون تغيير (30 خلية عصبية مخفية ، سرعة التعلم 0.5 ، حجم الرزمة المصغرة 10) ، لكننا سندرس 30 عصور باستخدام جميع الصور البالغ عددها 50000 صورة. فيما يلي رسم بياني يوضح دقة التصنيف في بيانات التدريب وبيانات الاختبار. لاحظ أنني استخدمت هنا بيانات التحقق من الصحة بدلاً من استخدام بيانات التحقق من الصحة لتسهيل مقارنة النتائج مع الرسوم البيانية السابقة.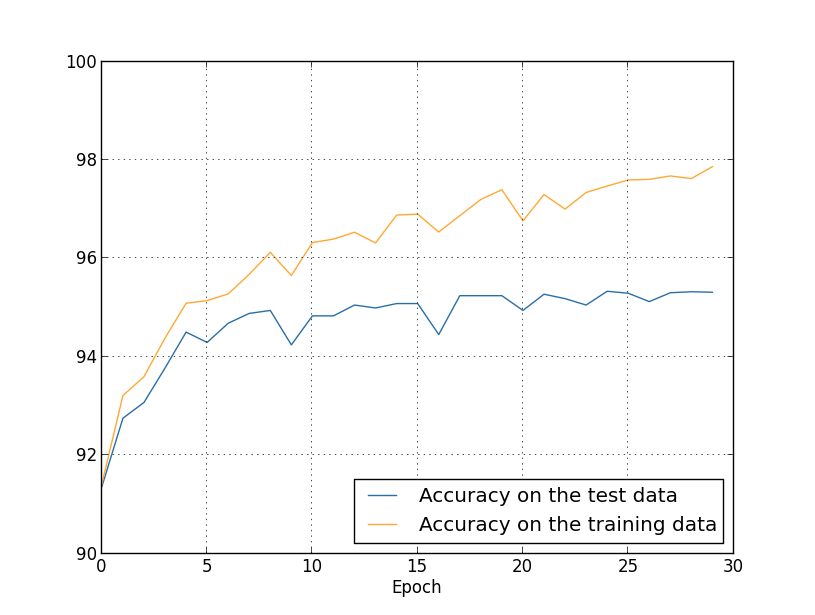



يمكن ملاحظة أن مؤشرات الدقة في الاختبار وبيانات التدريب تظل أقرب إلى بعضها البعض من عند استخدام 1000 مثال تدريبي. على وجه الخصوص ، دقة التصنيف الأفضل ، 97.86٪ ، أعلى بنسبة 2.53٪ فقط من 95.33٪ من بيانات التحقق. مقارنة مع استراحة مبكرة من 17.73 ٪! تتم إعادة التدريب ، ولكنها تقل بدرجة كبيرة. تقوم شبكتنا بتجميع المعلومات بشكل أفضل ، حيث تنتقل من التدريب إلى بيانات الاختبار. بشكل عام ، تتمثل إحدى أفضل الطرق لتقليل إعادة التدريب في زيادة كمية بيانات التدريب. مع وجود بيانات تدريب كافية ، من الصعب إعادة تدريب شبكة كبيرة جدًا. لسوء الحظ ، الحصول على بيانات التدريب مكلف و / أو صعب ، لذلك هذا الخيار ليس دائمًا عمليًا.

تسوية

زيادة كمية بيانات التدريب هي طريقة واحدة للحد من إعادة التدريب. هل هناك طرق أخرى للحد من إعادة التدريب؟ أحد الأساليب الممكنة هو تقليل حجم الشبكة. صحيح أن الشبكات الكبيرة لديها إمكانات أكثر من الشبكات الصغيرة ، لذلك نحن مترددون في اللجوء إلى هذا الخيار.

لحسن الحظ ، هناك تقنيات أخرى يمكن أن تقلل من إعادة التدريب ، حتى عندما نصلح حجم الشبكة وبيانات التدريب. وهي معروفة باسم تقنيات التنظيم. في هذا الفصل ، سوف أصف واحدة من أكثر التقنيات شعبية ، والتي تسمى أحيانًا الأوزان الضعيفة ، أو تنظيم L2. فكرتها هي إضافة عضو إضافي يسمى عضو التنظيم إلى دالة التكلفة. هنا عبر إنتروبيا مع التنظيم:

$$

$$C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2 \tag{85}$$

المصطلح الأول هو تعبير شائع عن إنتروبيا. لكن أضفنا ثانية ، وهي مجموع المربعات من جميع الأوزان الشبكة. يتم قياسه بواسطة العامل λ / 2n ، حيث λ> 0 هي معلمة التنظيم ، و n ، كالعادة ، هو حجم مجموعة التدريب. سنناقش كيفية اختيار λ. تجدر الإشارة أيضًا إلى أن التحيزات ليست مدرجة في مصطلح التنظيم. عن ذلك أدناه.

بالطبع ، من الممكن تنظيم وظائف التكلفة الأخرى ، على سبيل المثال ، من الدرجة الثانية. يمكن القيام بذلك بطريقة مماثلة:

$$

$$C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2 \tag{86}$$

في كلتا الحالتين ، يمكننا كتابة وظيفة التكلفة المنظمة مثل

$$

$$C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \tag{87}$$

حيث C ₀ هي دالة التكلفة الأصلية دون تنظيم.

من الواضح بشكل حدسي أن الهدف من التنظيم هو إقناع الشبكة بتفضيل الأوزان الأصغر ، وكل الأشياء الأخرى متساوية. لن تكون الأوزان الكبيرة ممكنة إلا إذا حسنت بشكل كبير الجزء الأول من دالة التكلفة. بمعنى آخر ، فإن التنظيم هو وسيلة لاختيار حل وسط بين إيجاد أوزان صغيرة وتقليل وظيفة التكلفة الأولية. من المهم أن يعتمد هذان عنصرا التسوية على قيمة λ: عندما تكون λ صغيرة ، نفضل تقليل دالة التكلفة الأصلية ، وعندما تكون λ كبيرة ، نفضل الأوزان الصغيرة.

ليس واضحًا على الإطلاق لماذا يجب أن يساعد اختيار مثل هذا الحل في تقليل إعادة التدريب! ولكن اتضح أنه يساعد. سنكتشف لماذا يساعد في القسم التالي. ولكن أولاً ، دعنا نعمل مع مثال يوضح أن التنظيم يقلل من إعادة التدريب.

لإنشاء مثال ، نحتاج أولاً إلى فهم كيفية تطبيق خوارزمية التدريب مع النسب التدرج العشوائي على NS منتظم. على وجه الخصوص ، نحتاج إلى معرفة كيفية حساب المشتقات الجزئية و /C / ∂w و ∂C / ∂b لجميع الأوزان والإزاحة في الشبكة. بعد أخذ المشتقات الجزئية في المعادلة (87) نحصل على:

$$

$$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}$$

$$

$$\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \tag{89}$$

يمكن حساب المصطلحين 0C ₀ / ∂w و ∂C ₀ / ∂w من خلال OP ، كما هو موضح في الفصل السابق. نرى أنه من السهل حساب التدرج اللوني لوظيفة التكلفة المنتظمة: تحتاج فقط إلى استخدام OP كالمعتاد ، ثم قم بإضافة λ / nw إلى المشتق الجزئي لكل مصطلحات الوزن. لا تتغير المشتقات الجزئية فيما يتعلق بحالات النزوح ، وبالتالي ، فإن قاعدة التعلم عن طريق النزول التدريجي للنزوح لا تختلف عن المعتادة:

$$

$$b \rightarrow b -\eta \frac{\partial C_0}{\partial b} \tag{90}$$

تتحول قاعدة التدريب الخاصة بالأوزان إلى:

$$

$$w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}$$

$$

$$= \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w} \tag{92}$$

كل شيء هو نفسه كما هو الحال في قاعدة نزول التدرج المعتاد ، إلا أننا نقوم أولاً بتقييم الوزن w بعامل 1 - ηλ / n. يسمى هذا التحجيم أحيانًا فقدان الوزن ، لأنه يقلل من الوزن. للوهلة الأولى ، يبدو أن الأوزان تميل بشكل لا يقاوم إلى الصفر. لكن هذا ليس صحيحًا ، لأن المصطلح الآخر يمكن أن يؤدي إلى زيادة الأوزان إذا كان هذا يؤدي إلى انخفاض في تكلفة التكلفة غير النظامية.

حسنًا ، اسمح لنسب التدرج مثل هذا. ماذا عن هبوط التدرج العشوائي؟ حسنًا ، كما هو الحال في الإصدار غير المنتظم من أصل التدرج العشوائي ، يمكننا تقدير ∂C ₀ / ∂w من خلال حساب المتوسط ​​على الحزمة المصغرة من أمثلة التدريب m. لذلك ، تتحول قاعدة التعلم النظامية لنسب التدرج العشوائي إلى (انظر المعادلة (20)):

$$

$$w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w} \tag{93}$$

حيث يذهب المبلغ للحصول على أمثلة التدريب x في الحزمة المصغرة ، و C _x هي التكلفة غير المنتظمة لكل مثال تدريب. كل شيء هو نفسه كما هو الحال في القاعدة المعتادة للنسب الانحداري العشوائي ، باستثناء 1 - ηλ / ن ، عامل فقدان الوزن. أخيرًا ، لإكمال الصورة ، اسمحوا لي أن أكتب قاعدة منتظمة للإزاحة. بطبيعة الحال ، هو بالضبط نفس الحالة في الحالة غير المنتظمة (انظر المعادلة (21)):

$$

$$b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b} \tag{94}$$

حيث يذهب المبلغ للحصول على أمثلة التدريب x في الحزمة المصغرة.

دعونا نرى كيف يغير التنظيم فعالية جمعيتنا الوطنية. سوف نستخدم شبكة تضم 30 خلية عصبية مخفية وحزمة صغيرة بحجم 10 وسرعة تعلم تبلغ 0.5 وظيفة تكلفة مع إنتروبيا. ومع ذلك ، هذه المرة نستخدم معلمة التنظيم 0.1 = 0.1. في الكود ، قمت بتسمية هذا المتغير lmbda ، لأن كلمة lambda محجوزة في بيثون للأشياء التي لا تتعلق بموضوعنا. لقد استخدمت أيضًا test_data مرةً أخرى بدلاً من validation_data. لكنني قررت استخدام test_data ، لأنه يمكن مقارنة النتائج مباشرةً مع النتائج المبكرة وغير المنتظمة. يمكنك بسهولة تغيير الرمز بحيث يستخدم validation_data والتأكد من أن النتائج متشابهة.

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, ... evaluation_data=test_data, lmbda = 0.1, ... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, ... monitor_training_cost=True, monitor_training_accuracy=True) 

إن تكلفة بيانات التدريب تتناقص باستمرار ، كما في الحالة السابقة ، دون تنظيم:



ولكن هذه المرة ، تستمر دقة بيانات الاختبار في الزيادة في جميع فترات الـ 400: من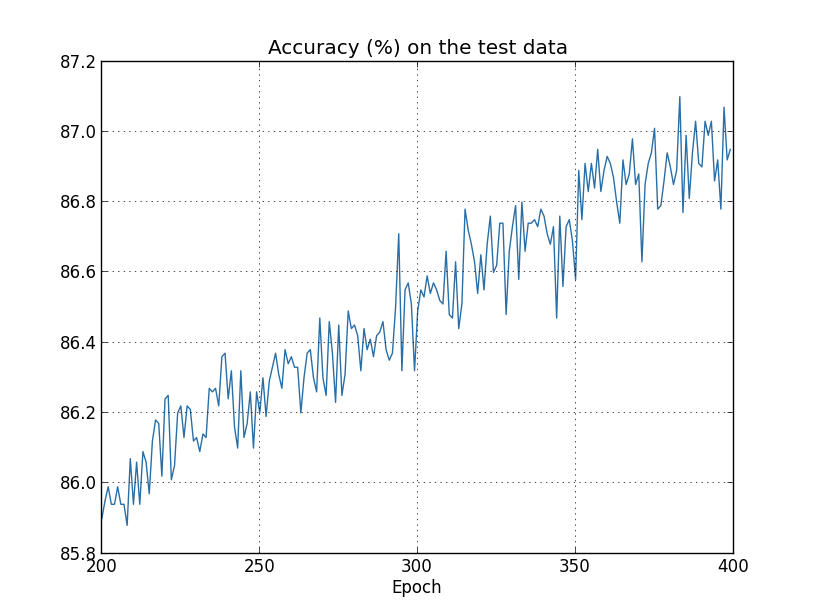



الواضح أن التنظيم أعيد تدريبه. علاوة على ذلك ، زادت الدقة بشكل كبير ، ووصلت دقة تصنيف الذروة إلى 87.1 ٪ ، مقارنة مع ذروة 82.27 ٪ التي تحققت في القضية دون تنظيم. بشكل عام ، من شبه المؤكد أننا نحقق نتائج أفضل من خلال الاستمرار في الدراسة بعد 400 عصر. من الناحية التجريبية ، يبدو أن التنظيم يجعل شبكتنا تعميم المعرفة بشكل أفضل ، ويقلل بشكل كبير من آثار إعادة التدريب.

ماذا يحدث إذا تركنا بيئتنا الصناعية ، التي تستخدم 1000 صورة تعليمية فقط ، والعودة إلى المجموعة الكاملة التي تضم 50000 صورة؟ بالطبع ، لقد رأينا بالفعل أن إعادة التدريب هي مشكلة أصغر بكثير مع مجموعة كاملة من 50000 صورة. هل تساعد عملية التنظيم على تحسين النتيجة؟ دعنا نحتفظ بالقيم السابقة للمعلمات الفائقة - 30 حقبة ، والسرعة 0.5 ، وحجم الحزمة المصغرة 10. ومع ذلك ، نحتاج إلى تغيير معلمة التنظيم. والحقيقة هي أن حجم ن مجموعة التدريب قفز من 1000 إلى 50 000 ، وهذا يغير عامل إضعاف الأوزان 1 - ηλ / ن. إذا واصلنا استخدام λ = 0.1 ، فهذا يعني أن الأوزان تضعف بدرجة أقل ، ونتيجة لذلك ، ينخفض ​​تأثير التنظيم. نحن نعوض هذا من خلال قبول λ = 5.0.

حسنًا ، دعنا ندرب شبكتنا عن طريق إعادة تهيئة الأوزان أولاً:

 >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, ... evaluation_data=test_data, lmbda = 5.0, ... monitor_evaluation_accuracy=True, monitor_training_accuracy=True) 

نحصل على النتائج: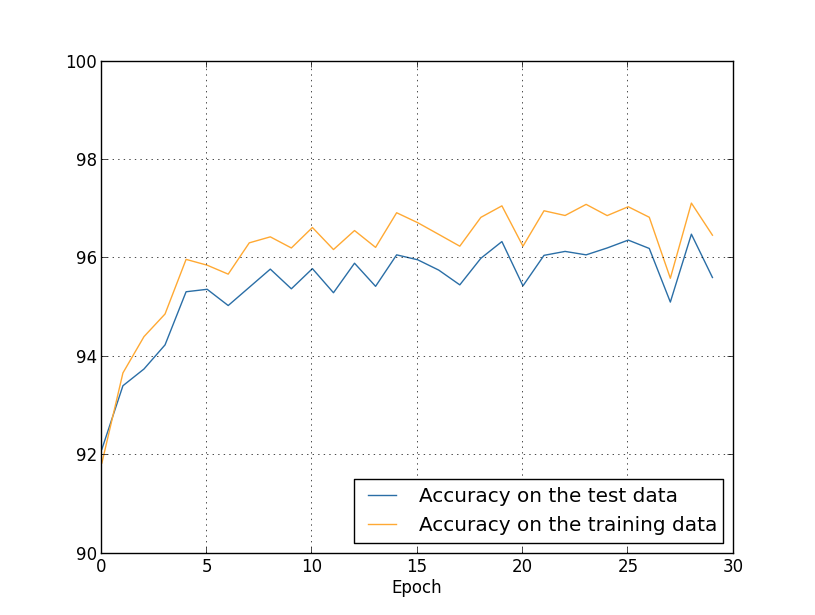



الكثير من الأشياء الممتعة. أولاً ، نمت دقة التصنيف الخاصة بنا على بيانات التحقق ، من 95.49٪ دون تنظيم إلى 96.49٪ مع التنظيم. هذا تحسن كبير. ثانياً ، يمكن ملاحظة أن الفجوة بين نتائج العمل على مجموعات التدريب والاختبار أقل بكثير من ذي قبل ، أي أقل من 1٪. ما زالت الفجوة لائقة ، لكن من الواضح أننا أحرزنا تقدماً كبيراً في الحد من إعادة التدريب.

أخيرًا ، انظر إلى دقة التصنيف التي نحصل عليها عند استخدام 100 خلية عصبية مخفية ومعلمة التنظيم & lambda = 5.0. لن أقدم تحليلاً مفصلاً لإعادة التدريب ، هذا فقط للمتعة ، لمعرفة مقدار الدقة التي يمكن تحقيقها من خلال الحيل الجديدة: دالة التكلفة مع إنتروبيا وترتيب L2.

 >>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

والنتيجة النهائية هي دقة تصنيف 97.92 ٪ على البيانات الداعمة. قفزة كبيرة مقارنة مع 30 خلية عصبية خفية. يمكنك ضبط أكثر من ذلك بقليل ، وبدء العملية لـ 60 فترة مع η = 0.1 و 5.0 = 5.0 ، والتغلب على حاجز 98 ٪ ، للوصول إلى دقة 98.04 على البيانات الداعمة. ليس سيئا ل 152 سطور من الكود!

وصفت التنظيم كوسيلة للحد من إعادة التدريب وزيادة دقة التصنيف. ولكن هذه ليست مزاياه الوحيدة. من الناحية التجريبية ، بعد تجربة العديد من عمليات إطلاق شبكتنا MNIST ، وتغيير الأوزان في كل مرة ، وجدت أن عمليات الإطلاق بدون تنظيم "تتعطل" في بعض الأحيان ، ومن الواضح أنها تقع في الحد الأدنى المحلي لوظيفة التكلفة. نتيجة لذلك ، أدت عمليات الإطلاق المختلفة في بعض الأحيان إلى نتائج مختلفة جدًا. وعلى العكس من ذلك ، يتيح لك التنظيم الحصول على نتائج قابلة للتكرار بسهولة أكبر.

لماذا هذا هكذا؟ من الناحية الاسترشادية ، عندما لا تكون دالة التكلفة منتظمة ، فإن طول متجه الأوزان سيزداد على الأرجح ، وكل الأشياء الأخرى متساوية. بمرور الوقت ، يمكن أن يؤدي هذا إلى ناقل كبير جدًا للأوزان. وبسبب هذا ، يمكن أن تتعطل متجهة المقاييس ، تظهر في نفس الاتجاه تقريبًا ، لأن التغييرات الناتجة عن نزول التدرج تؤدي إلى تغييرات صغيرة فقط في الاتجاه بطول كبير من المتجه. أعتقد أنه بسبب هذه الظاهرة ، من الصعب للغاية على خوارزمية التدريب لدينا دراسة مساحة الأوزان بشكل صحيح ، وبالتالي من الصعب العثور على حد أدنى جيد من وظيفة التكلفة.