الضوضاء في البيانات الكبيرة. تحليل الانتروبيا

صادفت مهمة تدعى اللجنة الرباعية Enscombe ( Anscombe ) ”( النسخة الإنجليزية ).

يوضح الشكل 1 توزيع جدولي ل 4 وظائف عشوائية (مأخوذة من ويكيبيديا).


التين. 1. جدول توزيع أربع وظائف عشوائية

يوضح الشكل 2 معلمات التوزيع لهذه الوظائف العشوائية


التين. 2. معلمات التوزيع من أربع وظائف عشوائية

والرسوم البيانية في الشكل 3.


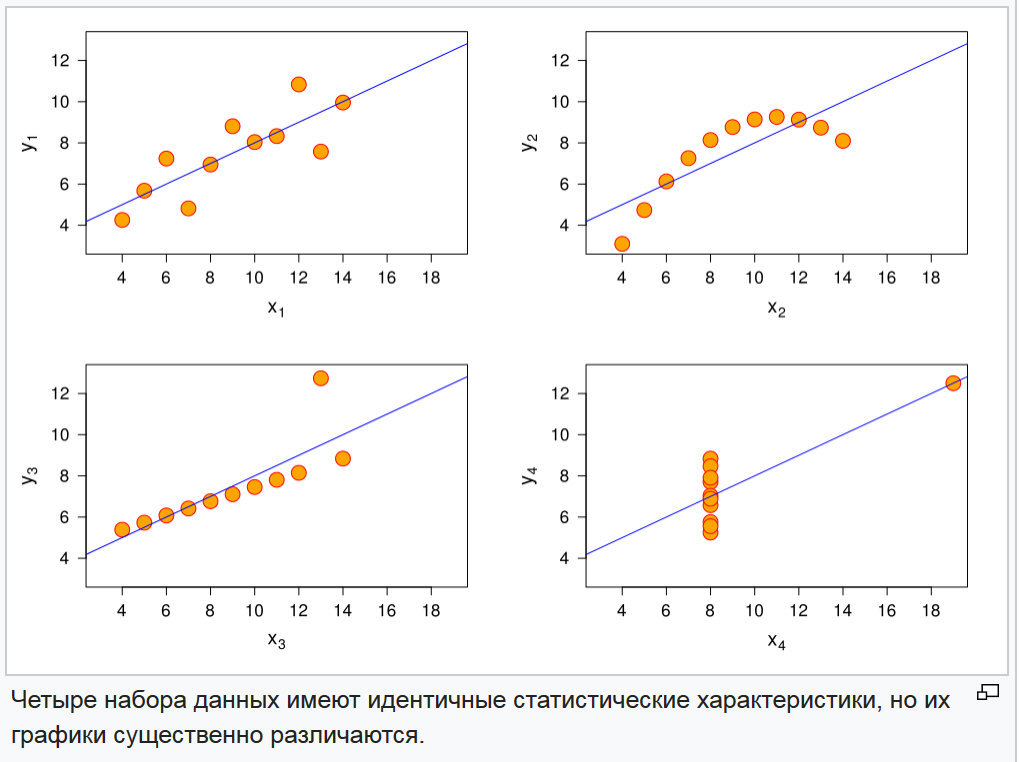التين. 3. الرسوم البيانية من أربع وظائف عشوائية

يتم حل مشكلة التمييز بين هذه الوظائف بكل بساطة من خلال مقارنة لحظات الطلبات الأعلى ومؤشراتها الطبيعية : معامل عدم التماثل والمعامل الزائد . وترد هذه المؤشرات في الشكل 4.


التين. 4. مؤشرات لحظات من الترتيب الثالث والرابع وعدم التماثل والمعاملات الزائدة من أربع وظائف عشوائية

كما يتضح من الجدول في الشكل 4 ، فإن مجموعة هذه المؤشرات لجميع الوظائف مختلفة.
الاستنتاج الأول ، الذي يشير بشكل طبيعي إلى أن المعلومات حول المواضع النسبية للنقاط يتم تخزينها في معلمات التوزيع بمستوى أعلى من التباين في التوزيع العشوائي.

يحاول العديد من المحللين عزل معادلات الانحدار المعينة في البيانات الكبيرة ، وحتى الآن ، هذه طريقة لتحديد المعادلة مع أصغر تشتت متبقٍ. لم يكن هناك الكثير لإضافته. لكنني لفتت الانتباه إلى حقيقة أن هذه هي كل المعلومات ، والمعلومات لديها مؤشر على الانتروبيا . ولها ، إنتروبيا ، حدودها من 0 ، عندما يتم تحديد المعلومات تماما للضوضاء البيضاء. والضوضاء البيضاء في قناة الإرسال لديها توزيع موحد.

عندما يكون مطلوبًا تحليل البيانات ، يُفترض في البداية أنها تحتوي على بيانات ذات صلة تحتاج إلى إضفاء الطابع الرسمي عليها كعلاقة. وهذا يشير إلى أن البيانات ليست ضوضاء بيضاء. بمعنى ، المرحلة الأولى هي اختيار معادلة الانحدار وتحديد التباين المتبقي. إذا تم اختيار الانحدار بشكل صحيح ، فإن التباين المتبقي سوف يطيع قانون التوزيع الطبيعي. دعونا نرى ، في الأشكال 5-7 ، يتم تقديم صيغ إنتروبيا لمتغير عشوائي موزعة بشكل موحد وزعت عادة.



التين. 5. صيغة إنتروبيا التفاضلية لكمية موزعة عادة (VV Afanasyev ، نظرية الاحتمالات في الأسئلة والمهام ، وزارة التعليم والعلوم في الاتحاد الروسي جامعة ياروسلافل التربوية الحكومية سميت باسم KD Ushinsky)


التين. 6. صيغة الانتروبيا التفاضلية لكمية موزعة بشكل طبيعي (Pugachev VS نظرية الوظائف العشوائية وتطبيقها على مشاكل التحكم الآلي . الطبعة الثانية ، المراجعة والمكملة. - M: Fizmatlit ، 1960. - 883 صفحة)


التين. 7. صيغة الانتروبيا التفاضلية لكمية موزعة بشكل موحد (Pugachev VS نظرية الوظائف العشوائية وتطبيقها على مشاكل التحكم الآلي ، الطبعة الثانية ، المراجعة والمكملة. - M: Fizmatlit ، 1960. - 883 صفحة)

بعد ذلك ، نعرض مثالا. لكن أولاً نأخذ الشروط التي تتمثل في أن كل وظيفة من الوظائف الأربع هي إحداثيات الطائرة الفائقة ، أي في نفس الوقت نتحقق من تشغيل النموذج في الفضاء متعدد الأبعاد. ارسم مجموعة من hypercube إلى مستوى الطائرة. يتم عرض الآلية في الشكل 8.




التين. 8. البيانات الأولية مع آلية الإلتواء


التين. 9. التجمع الكلي في الشكل.


التين. 10. معلمات توزيعات أربع وظائف عشوائية وتجميع موجز.

النظر في آلية لاختيار حجم الفاصل الزمني للقسم. ترد الشروط الأولية في الشكل 11.


التين. 11. الشروط الأولية للتقسيم إلى فترات.

الشرط 1. يجب أن يكون باحتمال غير صفري في منطقة التباين ، حيث إن الإنتروبيا تساوي اللانهاية. سواء بالنسبة للعينة الأولية وللباقي.

الشرط 2. نظرًا لأنه من المستحيل تجاهل إمكانية وجود بيانات خارجية جديدة ، وما إلى ذلك ، بالنسبة للفترات القصوى ، من الضروري إثبات الاحتمال وفقًا للقانون النظري العادي أو الآخر المقبول عمومًا لتوزيع الاحتمالات ، وفقًا لمبدأ احتمال المخلفات.

الحالة 3. يجب أن توفر خطوة الفاصل الحد الأدنى المطلوب من الفواصل الزمنية على انتشار العينة المتبقية.

الحالة 4. يجب أن يكون عدد الفواصل الزمنية غريبًا.

الحالة 5. يجب أن يضمن عدد الفواصل اتفاقًا موثوقًا به مع القانون النظري للتوزيع المختار للدراسة.


التين. 12. ما تبقى من التوزيع

تحديد آلية اختيار الفاصل الزمني في الشكل 13.


التين. 13. خوارزمية اختيار الفاصل

المشكلة الرئيسية ، في رأيي ، هي تحديد ما إذا كان يجب إدخال فترات زمنية نهائية أم لا. إذا كان التشتت المتبقي أمرًا طبيعيًا تمامًا ، فعندئذٍ بالنسبة إلى السلسلة الرئيسية ، يكون الأمر متوتراً للغاية.


التين. 14. نتائج معالجة قيم البيانات في تحديد إنتروبيا المعلومات

الاستنتاجات. أين يمكن تطبيق هذه الأداة

بمقارنة المؤشرات الناتجة في الجدول في الشكل 14 ، يمكن ملاحظة أنها استجابت للتغيير في بنية البيانات. وهذا يعني أن الأداة لها حساسية ، وتتيح لك حل المشكلات المشابهة لمهمة الرباعية Enskomb.

بدون شك ، يمكن حل هذه المشكلات بمساعدة لحظات الطلبات العليا. ولكن في جوهرها ، تعتمد إنتروبيا المعلوماتية على تباين المتغير العشوائي ، أي أنها سمة خارجية من أشكال التباين. لذلك ، يمكننا الإشارة إلى الفواصل الزمنية حيث يمكن أن يؤدي استخدام تحليل التباين إلى نتيجة محددة.

الخاصية العددية للإنتروبيا تجعل من الممكن إجراء تحليل الارتباط مع المتغيرات المستقلة. كمثال على مظهر من مظاهر اتصال ممكن ، ما يلي: افترض ، على مدى الفاصل من a إلى b ، زيادة مستوى الضوضاء لسلسلة من البيانات ، مقارنة قيم المتغيرات المستقلة ، وجدنا أن المتغير xn دخل نطاق أكثر من 5 وحدات ، بعده متغير ، انخفض أقل من +5 ، انخفض الضوضاء. علاوة على ذلك ، يمكن إجراء فحص إضافي ، وإذا تم تأكيد هذه الفرضية ، في دراسات أخرى ، يمنع المتغير xn من الارتفاع فوق +5. منذ في هذه الحالة ، تصبح البيانات عديمة الفائدة.

أفترض أن هناك خيارات أخرى لاستخدام هذه الأداة.

كيفية الاستخدام

في هذا الجانب ، يتم فحص الآلية الطبيعية لـ "المتوسط ​​المتحرك" ، أفترض أن حجم العينة الذي تم الحصول عليه من صيغة حجم العينة من التحليل الإحصائي سوف يعطي حجمًا معقولًا لمنطقة الانزلاق. وفقًا للتحليل الحالي ، تم استنتاج أنه يجب تحديد حجم العينة من النسبة الدنيا التي تقع على أقل احتمال. في مثالنا ، بالنسبة إلى التباين المتبقي ، يكون الحد الأدنى لكسر الفاصل التجريبي هو 0.15909. يجب أن يتم ذلك ، لأنه إذا تبين أن أي فاصل زمني في حجم الشريحة يكون فارغًا ، فسيكون رقم الضوضاء في هذه الحالة فاحشًا أو ستعمل القاعدة على أن تكون لوغاريثم 0 ناقصًا إلى ما لا نهاية. ومع وجود حجم عينة تم اختياره بشكل صحيح ، ستشير القيم المتعالية لهذا المؤشر إلى حدوث تغيير أساسي في بنية المعلومات.