أخذ العينات ودقة الحساب

يواجه عدد من زملائي مشكلة أنه من أجل حساب نوع من المقاييس ، على سبيل المثال ، معدل التحويل ، يجب عليك التحقق من قاعدة البيانات بأكملها. أو تحتاج إلى إجراء دراسة مفصلة لكل عميل ، حيث يوجد ملايين العملاء. يمكن لهذا النوع من كيري العمل لبعض الوقت ، حتى في مستودعات مصنوعة خصيصا. ليس من السهل للغاية الانتظار من 5 إلى 15 دقيقة حتى يتم اعتبار مقياس بسيط لمعرفة أنك تحتاج إلى حساب شيء آخر أو إضافة شيء آخر.

أحد الحلول لهذه المشكلة هو أخذ العينات: نحن لا نحاول حساب المقياس الخاص بنا على صفيف البيانات بأكمله ، ولكن نأخذ مجموعة فرعية تمثل المقاييس التي نحتاجها بشكل تمثيلي. يمكن أن تكون هذه العينة أصغر بمقدار 1000 مرة من مجموعة البيانات الخاصة بنا ، لكنها جيدة بما يكفي لإظهار الأرقام التي نحتاجها.

في هذه المقالة ، قررت توضيح كيف تؤثر أحجام عينات أخذ العينات على خطأ القياس النهائي.

المشكلة

والسؤال الرئيسي هو: إلى أي مدى تصف العينة "السكان"؟ نظرًا لأننا نأخذ عينة من مجموعة مشتركة ، فإن المقاييس التي نتلقاها تتحول إلى متغيرات عشوائية. عينات مختلفة سوف تعطينا نتائج متري مختلفة. مختلفة ، لا يعني أي. تخبرنا نظرية الاحتمالية أن القيم المترية التي تم الحصول عليها عن طريق أخذ العينات يجب تجميعها حول القيمة المترية الحقيقية (التي تم إجراؤها على العينة بأكملها) بمستوى معين من الخطأ. علاوة على ذلك ، لدينا غالبًا مشاكل حيث يمكن الاستغناء عن مستوى خطأ مختلف. إنه شيء واحد لمعرفة ما إذا كنا قد حصلنا على تحويل بنسبة 50 ٪ أو 10 ٪ ، وأنه شيء آخر للحصول على نتيجة بدقة 50.01 ٪ مقابل 50.02 ٪.

من المثير للاهتمام أنه من وجهة نظر النظرية ، فإن معامل التحويل الذي لاحظناه خلال العينة بأكملها هو أيضًا متغير عشوائي ، لأنه لا يمكن حساب معدل التحويل "النظري" إلا على عينة من الحجم غير المحدود. هذا يعني أنه حتى جميع ملاحظاتنا في قاعدة البيانات تعطي فعليًا تقدير التحويل بدقة ، على الرغم من أنه يبدو لنا أن هذه الأرقام المحسوبة دقيقة تمامًا. ويؤدي أيضًا إلى استنتاج أنه حتى لو كان معدل التحويل اليوم يختلف عن البارحة ، فإن هذا لا يعني أن شيئًا ما قد تغير ، ولكن يعني فقط أن العينة الحالية (جميع الملاحظات في قاعدة البيانات) هي من عامة السكان (كل ما هو ممكن) أعطت الملاحظات لهذا اليوم ، والتي وقعت ولم تحدث) نتيجة مختلفة قليلا عن أمس. في أي حال ، بالنسبة لأي منتج أو محلل صادق ، يجب أن تكون هذه فرضية أساسية.

بيان المهمة

لنفترض أن لدينا 1،000،000 سجل في قاعدة بيانات من النوع 0/1 ، والتي تخبرنا ما إذا كان قد حدث تحويل في حدث ما. ثم معدل التحويل هو ببساطة مجموع 1 مقسومًا على 1 مليون.

سؤال: إذا أخذنا عينة من الحجم N ، فما مدى احتمال اختلاف معدل التحويل عن المعدل المحسوب على العينة بأكملها ومع أي احتمال؟

اعتبارات نظرية

يتم تقليل المهمة لحساب فاصل الثقة لمعامل التحويل لعينة من حجم معين لتوزيع ذي حدين.

من الناحية النظرية ، فإن الانحراف المعياري للتوزيع ذي الحدين هو:
S = sqrt (p * (1 - p) / N)

حيث
ع - معدل التحويل
N - حجم العينة
S - الانحراف المعياري

لن أفكر في فاصل الثقة المباشر من النظرية. هناك matan معقدة إلى حد ما مربكة ، والذي يرتبط في نهاية المطاف الانحراف المعياري والتقدير النهائي لفاصل الثقة.

دعنا نطور "حدس" حول صيغة الانحراف المعياري:

1. أكبر حجم العينة ، أصغر الخطأ. في هذه الحالة ، يقع الخطأ في الاعتماد التربيعي العكسي ، أي زيادة العينة بمقدار 4 مرات يزيد من الدقة بمقدار 2 مرات فقط. وهذا يعني أن زيادة حجم العينة في مرحلة ما لن يعطي أي مزايا خاصة ، ويعني أيضًا أنه يمكن الحصول على دقة عالية إلى حد ما باستخدام عينة صغيرة إلى حد ما.

1. هناك اعتماد للخطأ على قيمة معدل التحويل. الخطأ النسبي (أي نسبة الخطأ إلى قيمة معدل التحويل) لديه ميل "خاطئ" ليكون أكبر ، كلما انخفض معدل التحويل:

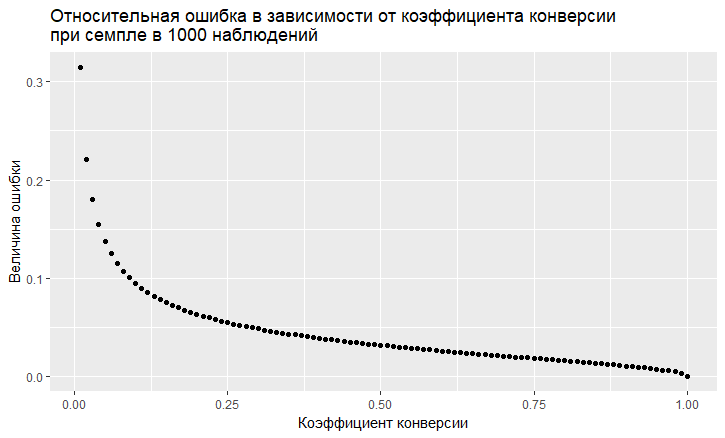
1. كما نرى ، الخطأ "يطير" إلى السماء مع انخفاض معدل التحويل. هذا يعني أنك إذا قمت بتجربة أحداث نادرة ، فأنت بحاجة إلى أحجام عينات كبيرة ، وإلا فسوف تحصل على تقدير تحويل مع وجود خطأ كبير جدًا.

تصميم

يمكننا الابتعاد تمامًا عن الحل النظري وحل المشكلة "وجهاً لوجه". بفضل لغة البحث والتطوير ، أصبح هذا سهلًا جدًا الآن. للإجابة على السؤال ، ما الخطأ الذي نحصل عليه عند أخذ العينات ، يمكنك فقط إجراء ألف عينة ومعرفة الخطأ الذي نحصل عليه.

النهج هو هذا:

1. نحن نأخذ معدلات تحويل مختلفة (من 0.01 ٪ إلى 50 ٪).
2. نحن نأخذ 1000 عينة من 10 ، 100 ، 1000 ، 10000 ، 50،000 ، 100،000 ، 250،000 ، 500،000 عنصر في العينة
3. نحسب معدل التحويل لكل مجموعة من العينات (1000 معاملات)
4. نحن نبني رسم بياني لكل مجموعة من العينات ونحدد مدى وجود 60 ٪ و 80 ٪ و 90 ٪ من معدلات التحويل الملحوظة.

R رمز توليد البيانات:

sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000) bootstrap = 1000 Error <- NULL len = 1000000 for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){ CRsub <- data.table(sample_size = 0, CR = 0) v1 = seq(1,len) v2 = rbinom(len, 1, prob) set = data.table(index = v1, conv = v2) print(paste('probability is: ', prob)) for (j in 1:length(sample.size)){ for(i in 1:bootstrap){ ss <- sample.size[j] subset <- set[round(runif(ss, min = 1, max = len),0),] CRsample <- sum(subset$conv)/dim(subset)[1] CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample)) } print(paste('sample size is:', sample.size[j])) q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95)) Error <- rbind(Error, cbind(prob,ss,t(q))) } 

نتيجة لذلك ، نحصل على الجدول التالي (سيكون هناك رسوم بيانية في وقت لاحق ، ولكن التفاصيل تكون مرئية بشكل أفضل في الجدول).

دعونا نرى الحالات مع تحويل 10 ٪ ومع تحويل 0.01 ٪ منخفضة ، ل جميع ميزات العمل مع أخذ العينات واضحة للعيان عليها.

عند التحويل بنسبة 10٪ ، تبدو الصورة بسيطة جدًا:

النقاط هي حواف فاصل الثقة 5-95 ٪ ، أي عند إجراء عينة ، سنحصل في 90٪ من الحالات على السجل التجاري للعينة ضمن هذا الفاصل الزمني. المقياس العمودي - حجم العينة (مقياس لوغاريتمي) ، قيمة معدل التحويل الأفقي. الشريط العمودي هو CR "حقيقي".

نرى نفس الشيء الذي رأيناه من النموذج النظري: تزداد الدقة مع نمو حجم العينة ، ويتقارب المرء بسرعة كبيرة وتصبح العينة قريبة من "صواب". في المجموع 1000 عينة لدينا 8.6 ٪ - 11.7 ٪ ، والتي ستكون كافية لعدد من المهام. وفي 10 ألف بالفعل 9.5 ٪ - 10.55 ٪.

الأمور أسوأ مع الأحداث النادرة وهذا يتوافق مع النظرية:

عند معدل تحويل منخفض يبلغ 0.01٪ ، تكمن المشكلة في وجود إحصائيات حول مليون ملاحظة ، أما بالنسبة للعينات ، فالوضع أسوأ. الخطأ هو مجرد عملاق. بالنسبة للعينات التي تصل إلى 10000 ، فإن المقياس غير صالح من حيث المبدأ. على سبيل المثال ، في عينة من 10 ملاحظات ، حصل المولد الخاص بي على تحويل صفر 1000 مرة ، لذلك هناك نقطة واحدة فقط. عند 100 ألف ، لدينا مبعثر من 0.005 ٪ إلى 0.0016 ٪ ، أي يمكننا أن نجعل ما يقرب من نصف معامل مع أخذ العينات من هذا القبيل.

تجدر الإشارة أيضًا إلى أنه عندما تلاحظ تحويل مثل هذا النطاق الصغير إلى مليون تجربة ، يكون لديك خطأ طبيعي كبير. يستنتج من ذلك أنه يجب إجراء استنتاجات حول ديناميات مثل هذه الأحداث النادرة على عينات كبيرة حقًا ، وإلا فإنك ستلاحق ببساطة الأشباح ، والتقلبات العشوائية في البيانات.

الاستنتاجات:

1. أخذ عينات من طريقة العمل للحصول على تقديرات
2. تزداد دقة العينة بزيادة حجم العينة وتقل مع انخفاض معدل التحويل.
3. يمكن تصميم دقة التقديرات لمهمتك ، وبالتالي اختيار أخذ العينات الأمثل لنفسك.
4. من المهم أن تتذكر أن الأحداث النادرة لا تكتسي جيدًا
5. بشكل عام ، يصعب تحليل الأحداث النادرة ؛ فهي تتطلب عينات بيانات كبيرة بدون عينات.