تحويل الصورة إلى صوت - ماذا يمكنك أن تسمع؟

مرحباً هبر.

وصف منشور حديث هنا على الموقع جهازًا يسمح للمكفوفين "برؤية" صورة ، وتحويلها باستخدام الموجات الصوتية. من الناحية الفنية ، لم تكن هناك في هذه المقالة أية تفاصيل على الإطلاق ( ماذا لو سُرقت فكرة المليون ) ، لكن المفهوم ذاته بدا مثيراً للاهتمام. بعد أن اكتسبت بعض الخبرة في معالجة الإشارات ، قررت أن أجربها بنفسي.



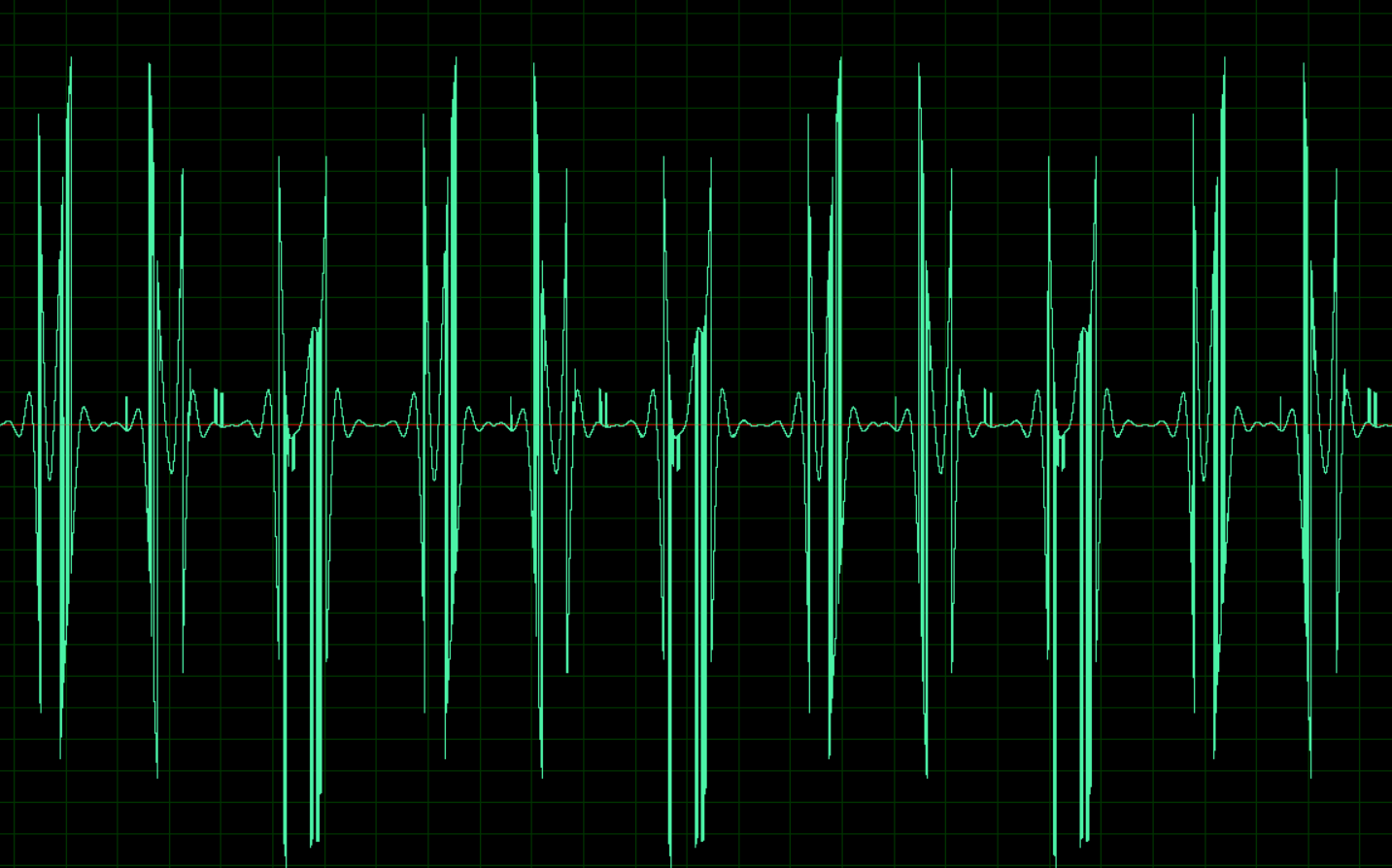
ما جاء منه ، تفاصيل وأمثلة من الملفات تحت القط.

تحويل 2D إلى 1D

تتمثل المهمة الأولى الواضحة التي تنتظرنا في تحويل صورة "مسطحة" ثنائية الأبعاد إلى موجة صوتية "أحادية البعد". كما هو مقترح في التعليقات على تلك المقالة ، من المريح استخدام منحنى هيلبرت لهذا الغرض.

إنها تشبه الكسرية بشكل أساسي ، والفكرة هي أنه مع زيادة دقة الصورة ، لا يتغير الموضع النسبي للكائنات (إذا كان الكائن في الركن الأيسر العلوي من الصورة ، فسيبقى هناك ). يمكن أن تمنحنا الأبعاد المختلفة لمنحنيات Hilbert صورًا مختلفة: 32 × 32 لـ N = 5 ، و 64 × 64 لـ N = 6 ، وهكذا. عن طريق "التجول" على طول هذا المنحنى ، نحصل على خط ، كائن أحادي البعد.

السؤال التالي هو حجم الصورة. أريد بشكل حدسي التقاط صورة أكبر ، لكن هناك "كبير": حتى الصورة 512 × 512 ، تبلغ 262144 بكسل. إذا قمنا بتحويل كل نقطة إلى نبضة صوتية ، فحينئذٍ على تردد أخذ العينات يبلغ 44100 ، نحصل على تسلسل يصل إلى 6 ثوانٍ ، وهذا طويل جدًا - يجب تحديث الصور بسرعة ، على سبيل المثال باستخدام كاميرا ويب. ليس من المنطقي جعل معدل أخذ العينات أعلى ، حيث نحصل على ترددات فوق صوتية غير مسموعة من الأذن (على الرغم من أنها قد تعمل من أجل بومة أو مضرب). كنتيجة لذلك ، تم اختيار دقة 128 × 128 بواسطة طريقة التبخير العلمي ، والتي ستعطي نبضات 0.37c - من ناحية ، فهي سريعة بما يكفي للتنقل في الوقت الحقيقي ، ومن ناحية أخرى ، تكفي لالتقاط أي تغييرات في شكل الإشارة عن طريق الأذن.

معالجة الصور

الخطوة الأولى هي تنزيل الصورة وتحويلها إلى b / w وتغيير حجمها إلى الحجم المطلوب. يعتمد حجم الصورة على بعد منحنى هيلبرت.

from PIL import Image from hilbertcurve.hilbertcurve import HilbertCurve import numpy as np from scipy.signal import butter, filtfilt # Create Hilbert curve dimension = 7 hilbert = HilbertCurve(dimension, n=2) print("Hilbert curve dimension:", dimension) # Maximum distance along curve print("Max_dist:", hilbert.max_h) # Maximum distance along curve print("Max_coord:", hilbert.max_x) # Maximum coordinate value in any dimension # Load PIL image f_name = "image01.png" img = Image.open(f_name) width, height = img.size out_size = hilbert_curve.max_x + 1 if width != out_size: img = img.resize((out_size, out_size), Image.ANTIALIAS) # Get image as grayscale numpy array img_grayscale = img.convert(mode='L') img_data = np.array(img_grayscale) 

الخطوة التالية هي تشكيل موجة صوتية. هنا ، بالطبع ، يمكن أن يكون هناك عدد كبير من الخوارزميات والدراية الفنية ، للاختبار لقد أخذت مكون السطوع. بالطبع ، ربما هناك طرق أفضل.

 width, height = img_grayscale.size sound_data = np.zeros(width*height) for ii in range(width*height): coord_x, coord_y = hilbert_curve.coordinates_from_distance(ii) pixel_l = img_data[coord_x][coord_y] # Inverse colors (paper-like, white = 0, black = 255) pixel_l = 255 - pixel_l # Adjust values 0..255 to 0..8192 ampl = pixel_l*32 sound_data[ii] = ampl 

من الكود ، أتمنى أن يكون كل شيء واضحًا. تقوم وظيفة coordinates_from_distance بكل عملنا على تحويل الإحداثيات (x ، y) إلى مسافة على منحنى Hilbert ، فنحن نقلب ونحول قيمة السطوع L إلى لون.

هذا ليس كل شيء. لأن قد يكون هناك كتل كبيرة من نفس اللون في الصورة ، وهذا يمكن أن يؤدي إلى ظهور "مكون العاصمة" في الصوت - سلسلة طويلة من القيم غير الصفر ، على سبيل المثال [100،100،100 ، ...]. لإزالتها ، نطبق مرشحًا عالي المرور (مرشح Butterworth ) على صفيفنا بتردد قطع قدره 50 هرتز (تتزامن مع تردد الشبكة بشكل عشوائي). هناك توليفة من المرشحات في مكتبة scipy ، والتي سوف نستخدمها.

 def butter_highpass(cutoff, fs, order=5): nyq = 0.5 * fs normal_cutoff = cutoff / nyq b, a = butter(order, normal_cutoff, btype='high', analog=False) return b, a def butter_highpass_filter(data, cutoff, fs, order=5): b, a = butter_highpass(cutoff, fs, order) y = filtfilt(b, a, data) return y # Apply high pass filter to remove dc component cutoff_hz = 50 sample_rate = 44100 order = 5 wav_data = butter_highpass_filter(sound_data, cutoff_hz, sample_rate, order) 

الخطوة الأخيرة هي حفظ الصورة. لأن طول النبضة قصيرة ، نكررها 10 مرات ، وسيكون أكثر سماعًا أقرب إلى صورة مكررة حقيقية ، على سبيل المثال من كاميرا ويب.

 # Clip data to int16 range sound_output = np.clip(wav_data, -32000, 32000).astype(np.int16) # Save repeat = 10 sound_output_ntimes = np.tile(sound_output, repeat) wav_name = "ouput.wav" scipy.io.wavfile.write(wav_name, sample_rate, sound_output_ntimes) 

النتائج

الخوارزمية أعلاه هي ، بطبيعة الحال ، بدائية للغاية. أردت التحقق من ثلاث نقاط - كم يمكنك التمييز بين الأشكال البسيطة المختلفة ، وكم يمكنك تقدير المسافة إلى الأشكال.

اختبار 1



تتوافق الصورة مع إشارة الصوت التالية:


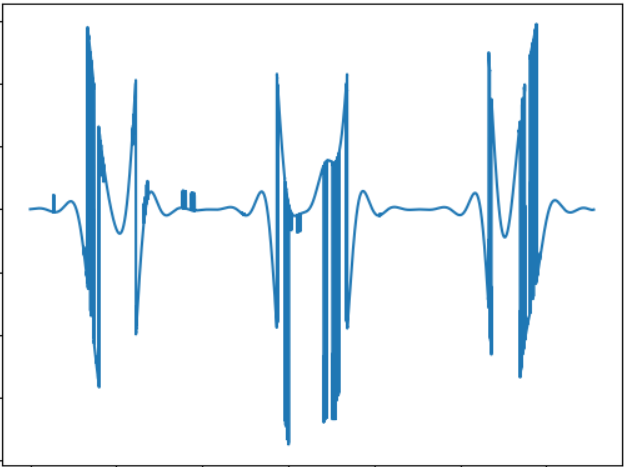
WAV: cloud.mail.ru/public/nt2R/2kwBvyRup

اختبار 2



فكرة هذا الاختبار هي مقارنة "صوت" كائن ذي شكل مختلف. إشارة الصوت:


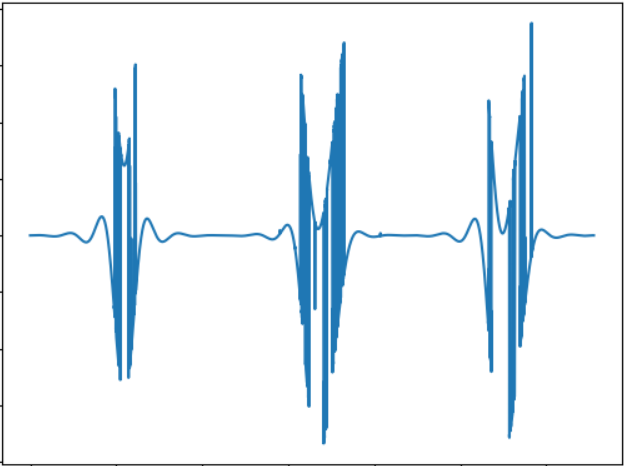
WAV: cloud.mail.ru/public/2rLu/4fCNRxCG2

قد تلاحظ أن الصوت مختلف حقًا ، وهناك اختلاف عن طريق الأذن.

اختبار 3



فكرة الاختبار هي اختبار كائن أصغر. إشارة الصوت:


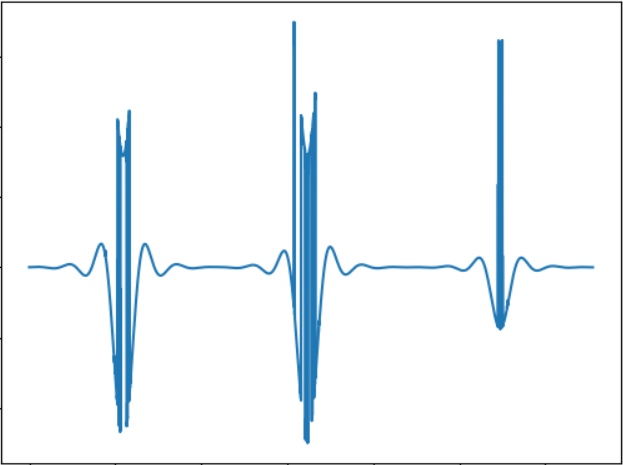
WAV: cloud.mail.ru/public/5GLV/2HoCHvoaY

من حيث المبدأ ، كلما كان حجم الكائن أصغر ، كلما كان هناك "رشقات" في الصوت ، وبالتالي فإن الاعتماد هنا مباشر تمامًا.

تحرير:

كما هو مقترح في التعليقات ، يمكنك استخدام تحويل فورييه لتحويل الصور مباشرة إلى صوت. يوضح الاختبار السريع الذي تم إجراؤه النتائج التالية (الصور متشابهة):
اختبار 1: cloud.mail.ru/public/2C5Z/5MEQ8Swjo
اختبار 2: cloud.mail.ru/public/2dxp/3sz8mjAib
اختبار 3: cloud.mail.ru/public/3NjJ/ZYrfdTYrk

تبدو الاختبارات مثيرة للاهتمام ، على الأقل للمربعات الصغيرة والكبيرة (الملفان 1 و 3) ، والفرق في السمع ملحوظ. لكن شكل الأشكال (1 و 2) من الناحية العملية لا يختلف ، لذلك هناك أيضًا شيء للتفكير فيه. ولكن بشكل عام ، الصوت الذي تم الحصول عليه باستخدام FFT ، عن طريق الأذن أحب أكثر.

استنتاج

هذا الاختبار ، بالطبع ، ليس أطروحة ، ولكنه مجرد دليل على المفهوم ، تم إجراؤه في ساعات قليلة من وقت الفراغ. ومع ذلك ، فإنه يعمل بشكل أساسي ، ومن الممكن تمامًا الشعور بالفرق عن طريق الأذن. لا أعرف ما إذا كان من الممكن تعلم التنقل في الفضاء بهذه الأصوات ، نظريًا ، ربما بعد بعض التدريب. على الرغم من وجود مجال كبير للتحسينات والتجارب ، على سبيل المثال ، يمكنك استخدام صوت ستريو ، والذي سيتيح لك فصل الكائنات عن الجوانب المختلفة بشكل أفضل ، إلا أنه يمكنك تجربة طرق أخرى لتحويل الصور إلى صوت ، على سبيل المثال ، تشفير الألوان بترددات مختلفة ، وما إلى ذلك. استخدام كاميرات ثلاثية الأبعاد قادرة على إدراك العمق (للأسف ، مثل هذه الكاميرا غير متوفرة). بالمناسبة ، بمساعدة رمز OpenCV بسيط ، يمكن تكييف الخوارزمية أعلاه لاستخدام كاميرا ويب ، والتي سوف تتيح لك تجربة الصور الديناميكية.

حسنا ، كالعادة ، كل التجارب الناجحة.