خوارزمية التشفير الجندب: فقط عن المجمع

توضح هذه المقالة تفاصيل خوارزمية تشفير البلوك المعرفة في GOST R 34.12-2015 باسم Grasshopper. ما الذي تستند إليه ، وما هي رياضيات خوارزميات تشفير البلوك ، وكيف يتم تنفيذ هذه الخوارزمية في جافا.

مَن ، وكيف ، ومتى ، ولماذا طورت هذه الخوارزمية التي ستظل خارج نطاق المقالة ، لأننا في هذه الحالة نحرص قليلًا ، باستثناء:

جندب = كوزنيتسوف ، نيتشيف أند كومباني.



نظرًا لأن التشفير يعتمد أساسًا على الرياضيات ، بحيث لا يتسبب التفسير الإضافي في الكثير من الأسئلة ، يجب أولاً تحليل المفاهيم الأساسية والوظائف الرياضية التي بنيت عليها هذه الخوارزمية.

الحقول جالوا

حساب حقول جالوا هو حساب متعدد الحدود ، أي أن كل عنصر من عناصر هذا الحقل متعدد الحدود. نتيجة أي عملية هي أيضا عنصر في هذا المجال. يتكون حقل غالوا معين من مجموعة ثابتة من الأرقام. وتسمى خاصية الحقل عدد أولي p. ترتيب الحقول ، أي كمية عناصرها هي درجة طبيعية معينة من الخصائص $$$p ^ m$ ، حيث m ϵ N. بالنسبة إلى m = 1 ، يُسمى الحقل بسيط. في الحالات التي تكون فيها m> 1 ، لتشكيل مجال ما ، هناك حاجة أيضًا إلى توليد متعدد الحدود من الدرجة m ؛ ويُسمى هذا الحقل ممتدًا. $$$Gf (p ^ m)$ - تعيين حقل جالوا. كثير الحدود المولدة غير قابلة للاختزال ، وهذا بسيط ، (بالقياس مع الأعداد الأولية ، يكون قابلاً للقسمة على 1 وفي حد ذاته دون الباقي). نظرًا لأن العمل مع أي معلومات يعمل مع وحدات البايت ، والبايت هو 8 بت ، خذ كحقل $$$Gf (2 ^ 8)$ وتوليد متعدد الحدود:

$$

$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$$

ومع ذلك ، بادئ ذي بدء ، سنقوم بتحليل العمليات الأساسية في مجال أبسط $$$Gf (2 ^ 3)$ مع توليد متعدد الحدود $$$f (x) = x ^ 3 + x + 1$ .

عملية إضافة

إن أبسطها هي عملية الإضافة ، والتي في حقل جالوا هي عبارة عن معامل إضافة بسيط في اتجاه حركة البت 2 (R).

أود على الفور لفت الانتباه إلى حقيقة أن علامة "+" هنا وهنا تشير إلى تشغيل XOR bitwise ، وليس الإضافة في الشكل المعتاد.

جدول الحقيقة لوظيفة HOR



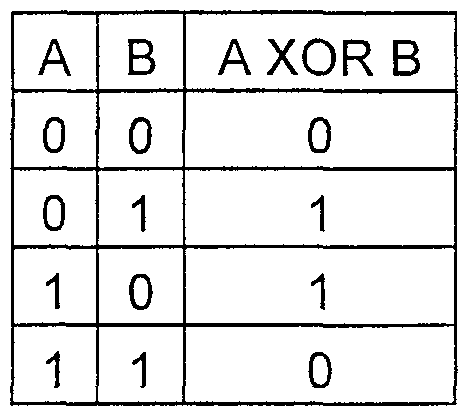
مثال: $$$5 + 3 = 101 + 011 = 110_2 = 6_ {10}$

في كثير الحدود ، ستبدو هذه العملية

$$

$$(x ^ 2 + 1) + (x + 1) = x ^ 2 + x = 110_2 = 6_ {10}$$

عملية الضرب

لتنفيذ عملية الضرب ، من الضروري تحويل الأرقام إلى شكل متعدد الحدود:

$$

$$5 = 101_2 = 1 * x ^ 2 + 0 * x ^ 1 + 1 * x ^ 0 = x ^ 2 + 1$$

كما ترون ، الرقم في كثير الحدود هو متعدد الحدود الذي معاملاته هي قيم الأرقام في التمثيل الثنائي للرقم.

اضرب رقمين في كثير الحدود:

$$

$$5 * 7 = (x ^ 2 + 1) * (x ^ 2 + x + 1) = x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x + 1 =$$

$$

$$= x ^ 4 + x ^ 3 + x + 1 = 11011_2 = 27_ {10}$$

نتيجة الضرب 27 ليست في الحقل المستخدم. $$$Gf (2 ^ 3)$ (يتكون من أرقام من 0 إلى 7 ، كما ذكر أعلاه). لمكافحة هذه المشكلة ، من الضروري استخدام متعدد الحدود توليد.

من المفترض أيضًا أن x يرضي المعادلة $$$f (x) = x ^ 3 + x + 1 = 0$ ثم



لنجعل جدول الضرب:



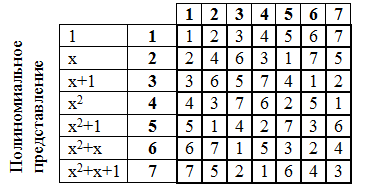
من الأهمية بمكان وجود جدول درجات عناصر حقل جالوا. كما يتم رفع القوة في كثير الحدود ، على غرار الضرب.

مثال:

$$

$$5 ^ 2 = (x ^ 2 + 1) ^ 2 = x ^ 4 + x ^ 2 + x ^ 2 + 1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 =$$

$$

$$= x (x ^ 3 + x + 1) + x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$$

وبالتالي ، نقوم بتجميع جدول الدرجات:



جدول الدرجة هو دوري: الدرجة السابعة تقابل الصفر ، وبالتالي فإن الثامن يتوافق مع الأول ، إلخ. يمكنك التحقق من هذا إذا كنت ترغب في ذلك.

في حقول غالوا ، هناك مفهوم للمصطلح البدائي - عنصر في حقل تحتوي درجته على جميع العناصر غير الصفرية للحقل. يمكن ملاحظة أن جميع العناصر تتوافق مع هذا الشرط (جيدًا ، باستثناء 1 ، بالطبع). ومع ذلك ، هذا ليس هو الحال دائما.

بالنسبة للحقول التي ندرسها ، أي ، مع الخاصية 2 ، اختر دائمًا 2. كعضو بدائي ، نظرًا لخصائصه ، يمكن التعبير عن أي عنصر في الحقل من حيث درجة العضو البدائي.



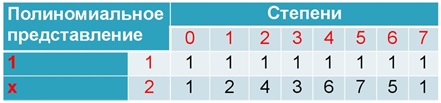
مثال: $$$5 = 2 ^ 6.7 = 2 ^ 5$

باستخدام هذه الخاصية ، ومع مراعاة الدورية لجدول الدرجات ، سنحاول ضرب الأرقام مرة أخرى:

$$

$$5 * 7 = 2 ^ 6 * 2 ^ 5 = 2 ^ {(6 + 5)} = 2 ^ {(11mod7)} = 2 ^ 4 = 6$$

تزامنت النتيجة مع ما حسبنا في وقت سابق.

الآن دعونا نفعل القسم:

$$

$$6/5 = 2 ^ 4/2 ^ 6 = 2 ^ {(4-6)} = 2 ^ {((- 2) mod7)} = 2 ^ 5 = 7$$

النتيجة التي تم الحصول عليها صحيحة أيضا.

حسنًا ، من أجل الاكتمال ، دعونا ننظر إلى رفع مستوى القوة:

$$

$$5 ^ 2 = (2 ^ 6) ^ 2 = 2 ^ {(6 * 2)} = 2 ^ {(12mod7)} = 2 ^ 5 = 7$$

مثل هذا النهج في الضرب والقسمة هو أبسط بكثير من العمليات الحقيقية باستخدام كثير الحدود ، وليس هناك حاجة لتخزين جدول الضرب الكبير ، ولكن مجرد صف من درجات عضو الحقل البدائي.

عاد الآن إلى مجالنا $$$Gf (2 ^ 8)$

عنصر الصفر في الحقل واحد ، الأول هو اثنان ، كل عنصر لاحق من العنصر 2 إلى 254 يتم حسابه باعتباره العنصر السابق ، مضروبًا في 2 ، وإذا كان العنصر خارج الحقل ، فستكون قيمته أكبر من $$$(2 ^ 8-1)$ ثم يتم XOR مع الرقم $$$195_ {10} دولا$ ، هذا الرقم يمثل كثير الحدود غير القابلة للاختزال من الحقل $$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1 = 2 ^ 8 + 2 ^ 7 ++ 2 ^ 6 + 2 + 1 = 451$ ، نأتي هذا الرقم إلى الميدان $$ . والعنصر 255 هو مرة أخرى 1. لذلك لدينا حقل يحتوي على 256 عنصرًا ، أي مجموعة كاملة من وحدات البايت ، وقمنا بتحليل العمليات الأساسية التي يتم تنفيذها في هذا الحقل.



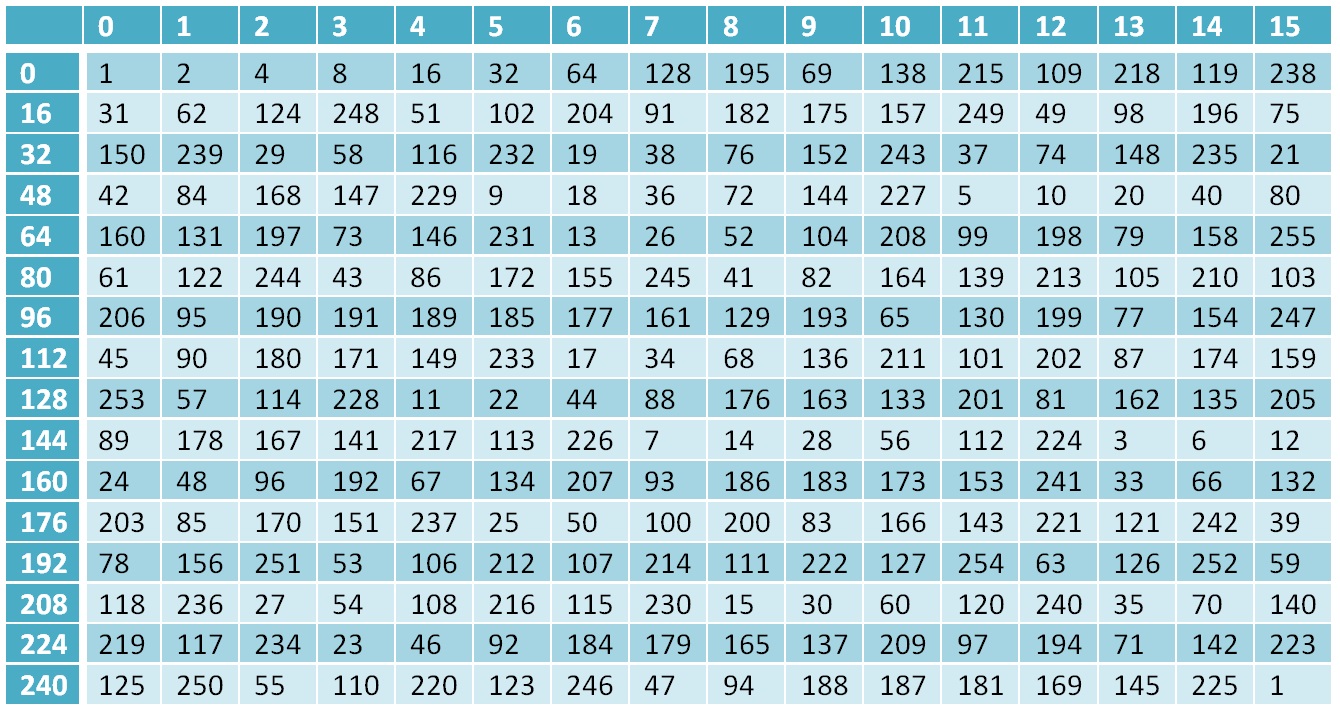
جدول صلاحيات اثنين لهذا المجال $$$Gf (2 ^ 8)$

سبب الحاجة - يتم إجراء جزء من العمليات الحسابية في خوارزمية Grasshopper في حقل Galois ، وتكون نتائج العمليات الحسابية بناءً على ذلك عناصر في هذا الحقل.

شبكة فيستل

Feistel Network هي طريقة تشفير بلوك طورتها شركة Horst Feistel في شركة IBM في عام 1971. شبكة Feistel اليوم هي أساس عدد كبير من بروتوكولات التشفير.

تعمل شبكة Feistel مع كتل نصية واضحة:

1. يتم تقسيم الكتلة إلى قسمين متساويين - اليسار L واليمين R.
2. يتم تغيير الكتلة الفرعية اليسرى L بواسطة الدالة f باستخدام المفتاح K: X = f (L، K). كدالة ، يمكن أن يكون هناك أي تحول.
3. تتم إضافة الكتلة الفرعية الناتجة X معامل 2 مع subblock الأيمن R ، الذي لم يتغير: X = X + R.
4. الأجزاء الناتجة متبادلة ولصقها.

هذا التسلسل من الإجراءات يسمى خلية Feistel.


الشكل 1. خلية Feistel

تتكون شبكة Feistel من عدة خلايا. تذهب القوالب الفرعية التي تم الحصول عليها عند إخراج الخلية الأولى إلى إدخال الخلية الثانية ، وتذهب القوالب الفرعية الناتجة من الخلية الثانية إلى إدخال الخلية الثالثة وما إلى ذلك.

خوارزمية التشفير

الآن أصبحنا على دراية بالعمليات المستخدمة ويمكننا الانتقال إلى الموضوع الرئيسي - وهي خوارزمية تشفير Grasshopper.

أساس الخوارزمية هو ما يسمى بشبكة SP - شبكة تبديل الإحلال. يتلقى التشفير القائم على شبكة SP كتلة ومفتاحًا عند الإدخال ويقوم بالعديد من جولات التناوب التي تتكون من مراحل الاستبدال ومراحل التقليب. يقوم Grasshopper بتسع جولات كاملة ، تشمل كل منها ثلاث عمليات متتالية:

1. تشغيل تطبيق مفتاح مستدير أو XOR bitwise للمفتاح وكتلة بيانات الإدخال ؛
2. تحويل غير خطي ، وهو بديل بسيط للبايت بأخرى وفقاً للجدول ؛
3. التحول الخطي. يتم ضرب كل بايت من الكتلة في حقل غالوا بواحد من معاملات السلسلة (148 ، 32 ، 133 ، 16 ، 194 ، 192 ، 1 ، 251 ، 1 ، 192 ، 194 ، 16 ، 133 ، 32 ، 148 ، 1) اعتمادًا على الترتيبي أرقام البايت (يتم تقديم سلسلة للأرقام التسلسلية من 15 إلى 0 ، كما هو موضح في الشكل). تتم إضافة وحدات البايت معًا للمعيار 2 ، ويتم تحويل جميع وحدات البايت 16 للكتلة باتجاه الترتيب المنخفض ، ويتم كتابة الرقم الناتج بدلاً من بايت القراءة.

الجولة العاشرة الأخيرة ليست كاملة ، فهي تشمل فقط عملية XOR الأولى.

Grasshopper عبارة عن خوارزمية كتلة ، وهي تعمل مع كتل بيانات يبلغ طولها 128 بت أو 16 بايت. طول المفتاح هو 256 بت (32 بايت).


الشكل 2. مخطط التشفير وفك التشفير من كتلة البيانات

يوضح الرسم البياني تسلسل العمليات ، حيث S عبارة عن تحويل غير خطي ، L عبارة عن تحويل خطي ، Ki هي مفاتيح مستديرة. السؤال الذي يطرح نفسه على الفور - من أين تأتي المفاتيح المستديرة.

تشكيل مفتاح الجولة

يتم الحصول على مفاتيح تكرارية (أو مستديرة) من خلال تحويلات معينة تستند إلى مفتاح رئيسي ، يبلغ طوله ، كما نعلم بالفعل ، 256 بت. تبدأ هذه العملية بتقسيم المفتاح الرئيسي إلى النصف ، بحيث يتم الحصول على الزوج الأول من المفاتيح المستديرة. تُستخدم ثماني تكرارات من شبكة Feistel لإنشاء كل زوج من المفاتيح الدائرية اللاحقة ، ويتم استخدام ثابت في كل تكرار ، ويتم حسابه عن طريق تطبيق تحويل خطي للخوارزمية على قيمة رقم التكرار.


مخطط الحصول على مفاتيح تكرارية (مستديرة)

إذا تذكرنا بالشكل 1 ، فإن الكتلة الفرعية اليسرى L هي النصف الأيسر من المفتاح الأصلي ، وتكون الكتلة الفرعية اليمنى R هي النصف الأيمن من المفتاح الأصلي ، K هي Ci الثابتة ، والوظيفة f هي تسلسل العمليات R XOR Ci ، والتحول غير الخطي ، والتحول الخطي.

يتم الحصول على ثوابت التكرار Ci باستخدام التحويل L لرقم تسلسل التكرار.

لذلك ، من أجل تشفير كتلة من النص ، نحتاج أولاً إلى حساب 32 ثوابت متكررة ، ثم حساب 10 مفاتيح دائرية بناءً على المفتاح ، ثم إجراء تسلسل العمليات الموضح في الشكل 2.

لنبدأ بحساب الثوابت:
أول const $$$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ ومع ذلك ، يتم تنفيذ جميع التحويلات في خوارزمية لدينا مع كتل من 16 بايت ، وبالتالي فمن الضروري أن تكملة ثابت مع طول الكتلة ، أي إضافة 15 صفر بايت إلى اليمين ، نحصل على

$$

اضربها بسلسلة (1 ، 148 ، 32 ، 133 ، 16 ، 194 ، 192 ، 1 ، 251 ، 1 ، 192 ، 194 ، 16 ، 133 ، 32 ، 148) على النحو التالي:

$$

$$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$$

$$

$$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

(يتم إعطاء هذه المساواة في عمليات حقول جالوا)
نظرًا لأن كل شيء ما عدا صفر بايت يساوي 0 ، وضرب بايت صفر في 1 ، نحصل على 1 ونكتبه بالترتيب العالي للرقم ، ونحول كل البايتات إلى الترتيب المنخفض ، نحصل على:

$$

كرر نفس العمليات. هذه المرة $$$a_ {15} = 1 دولا$ ، جميع البايتات الأخرى هي 0 ، لذلك ، يبقى الأول فقط من الشروط $$$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ حصلنا على:

$$

نقوم بالتكرار الثالث ، فيما يلي مصطلحين غير صفريين:

$$

$$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$$

$$

$$= 10010100 * 10010100 + 00000001 * 00100000 =$$

$$

$$= (x ^ 7 + x ^ 4 + x ^ 2) * (x ^ 7 + x ^ 4 + x ^ 2) + 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + س ^ 5 =$$

$$

$$= x ^ 6 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 5 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 3 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$$

$$

$$= x ^ 2 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$$

$$

$$132_ {10} = 84_ {16}$$

وفقًا لجدول الدرجات ، يمكن حلها بسهولة أكبر:

$$

$$

علاوة على ذلك ، كل شيء هو نفسه بالضبط ، فقط 16 تكرار لكل ثابت

$$

$$

$$

$$

$$

$$

$$

$$

$$

$$

$$

$$

والثابت النهائي:

$$

الثوابت الأخرى:

$$

$$

$$

$$

$$

$$

$$

$$

$$

$$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$$

$$

$$C_ {11} = 0B55E583B0A5924A82D8DD5280AC7C44$$

$$

$$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$$

$$

$$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$$

$$

$$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$$

$$

$$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$$

$$

$$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$$

$$

$$C_ {17} = 11C01393D33C12C469D642635E1A1041$$

$$

$$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$$

$$

$$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$$

$$

$$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$$

$$

$$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$$

$$

$$C_ {22} = 16AA09C5A389E794C77379A4C39BF888$$

$$

$$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$$

$$

$$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$$

$$

$$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$$

$$

$$C_ {26} = 1A95F6106399808EEB0E9F31DEB66C05$$

$$

$$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$$

$$

$$C_ {28} = 1C6B689B03915283FDD1EC9A314126A2$$

$$

$$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$$

$$

$$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$$

$$

$$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$$

$$

$$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$$

سنقوم الآن بحساب المفاتيح المستديرة وفقًا للمخطط الموضح أعلاه ، خذ مفتاح التشفير:

$$

$$

$$EFCDAB89674523011032547698BADCFE$$

ثم

$$

$$

$$$K_1$ ستكون الكتلة الفرعية اليسرى لشبكة Feistel و $$$K_2 دولا$ - صحيح.
دعونا نفعل العملية $$$K_1 + C_1$
البايت الأول $$$K_1$ يساوي $$$77_ {16} = 01110111_2$
البايت الأول $$$C_1$ يساوي $$$01_ {16} = 00000001_2$

$$

$$01110111_2 + 00000001_2 = 01110110_2 = 76_ {16}$$

يتم تحويل البايتات المتبقية بنفس الطريقة ، نتيجة لذلك $$ :

$$

$$X (K_1 ، C_1) = 76F2D199239F365D479495A0C9DC3BE6$$

بعد ذلك ، نقوم بإجراء تحول غير خطي $$$S (X (K_1 ، C_1))$ . يتم تنفيذها وفقا للجدول:


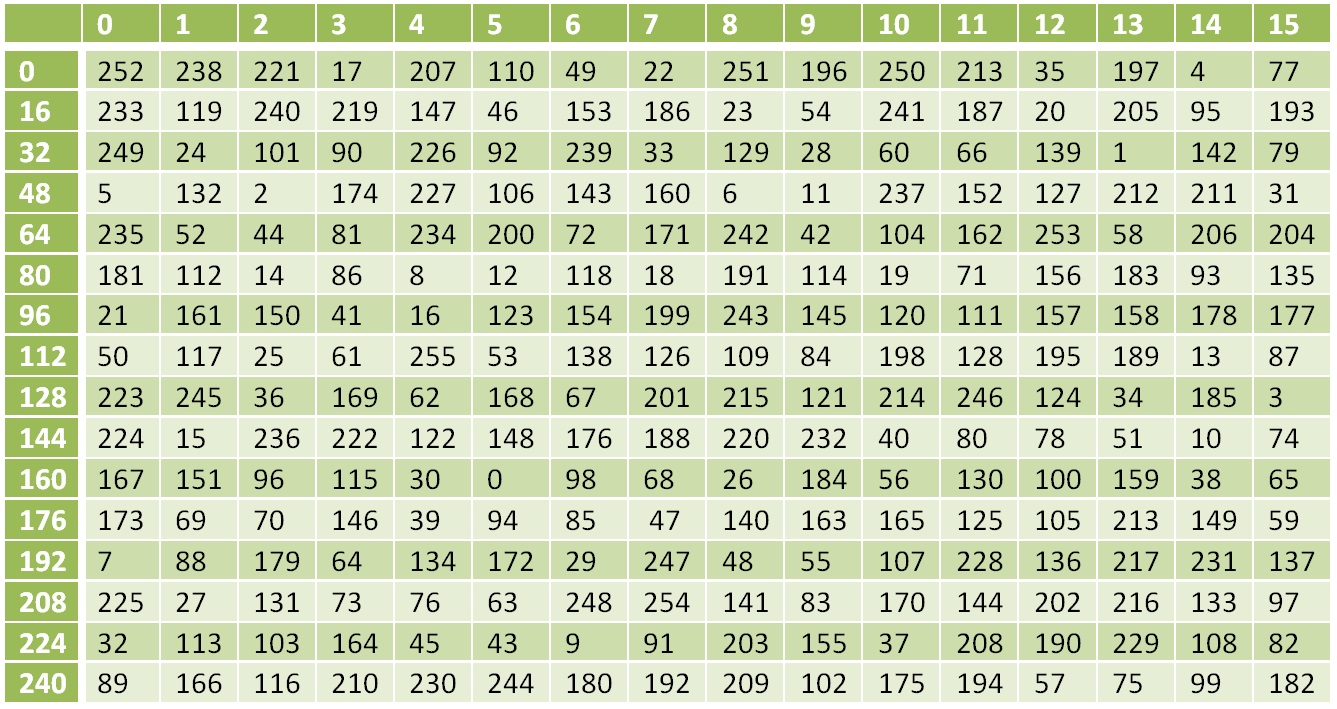جدول تحويل غير خطي

يتم استبدال الرقم 0 ب 252 ، 1 ب 238 ، 17 ب 119 ، إلخ.

$$

$$76_ {16} = 118_ {10}$$

$$

$$S (118) = 138_ {10} = 8A_ {16}$$

$$

$$S (X (K_1 ، C_1)) = 8A741BE85A4A8FB7AB7A94A737CA9809$$

الآن إجراء التحول الخطي $$$L (S (X (K_1 ، C_1)))$ ، تم النظر فيه بالتفصيل عند حساب الثوابت التكرارية ، لذلك نحن هنا نعطي النتيجة النهائية فقط:

$$

$$L (S (X (K_1، C_1))) = A644615E1D0757926A5DB79D9940093D$$

وفقًا لخطة خلية Feistel ، نقوم بإجراء XOR مع الكتلة الفرعية اليمنى ، على سبيل المثال ، مع $$$K_2 دولا$ :

$$

$$X (L (S (X (K_1 ، C_1))) ، K_2) = 4989CAD77A4274937A6FE3EB01FAD5C3$$

والنتيجة التي تم الحصول عليها في إخراج أول خلية فيستل:

$$

$$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$$

هذه القيمة إلى النصف وتذهب إلى إدخال خلية Feistel الثانية ، حيث يتم استخدام الثابت الثاني بالفعل $$ . بعد المرور عبر ثماني خلايا ، نحصل على المفتاحين التاليين $$$K_3 دولا$ و $$$K_4 دولا$ . سنقوم بإجراء ثماني تكرارات لشبكة Feistel معهم ، والحصول على زوج المفاتيح التالي ، وهكذا. ثماني تكرارات لكل زوج رئيسي ، نظرًا لأن لدينا في البداية الزوج الأول ، يتم تنفيذ 32 تكرارًا في المجموع ، لكل منها ثابتها الخاص.

المفاتيح المتبقية:

$$

$$

$$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$$

$$

$$

$$

$$

$$

$$K_9 = 17E5B6CD732FF3A52331C77853E244BB$$

$$

$$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$$

كتلة التشفير

لقد قمنا بحساب جميع المفاتيح ، وأخيراً يمكننا الآن الانتقال مباشرة إلى تشفير كتلة النص وإذا كنت تقرأ بعناية كل ما كتب أعلاه ، فلن يكون تشفير النص أمرًا صعبًا ، حيث أن جميع العمليات المستخدمة في هذه العملية وتسلسلها قد تم فحصها بالتفصيل.

خذ كتلة النص العادي:

$$

تنفيذ تسلسل العمليات X ، S ، L

$$

$$X (T، K_1) = FFFFFFFFFFFFFFFFFFFF99BB99FF99BB99$$

$$

$$S (X (T ، K_1)) = B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$$

$$

$$L (S (X (T، K_1))) = 30081449922F4ACFA1B055E386B697E2$$

$$

$$

$$X (T_1 ، K_2) = DFC5BFC0F56A69CEB18201951E0C4B1C$$

$$

$$S (X (T_1 ، K_2)) = 61AC3B07F47891E74524EE945F23A214$$

$$

$$L (S (X (T_1 ، K_2))) = 7290C6A158426FB396D562087A495E28$$

$$

وهكذا ، ستبدو النتيجة النهائية كما يلي:

$$

$$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$$

كتلة فك التشفير

لفك تشفير النص ، تحتاج إلى استخدام العمليات العكسية بالترتيب العكسي (انظر الشكل 2).

عملية XOR معكوسة لنفسها ، وعكس العملية S هي الاستبدال وفقًا للجدول التالي:


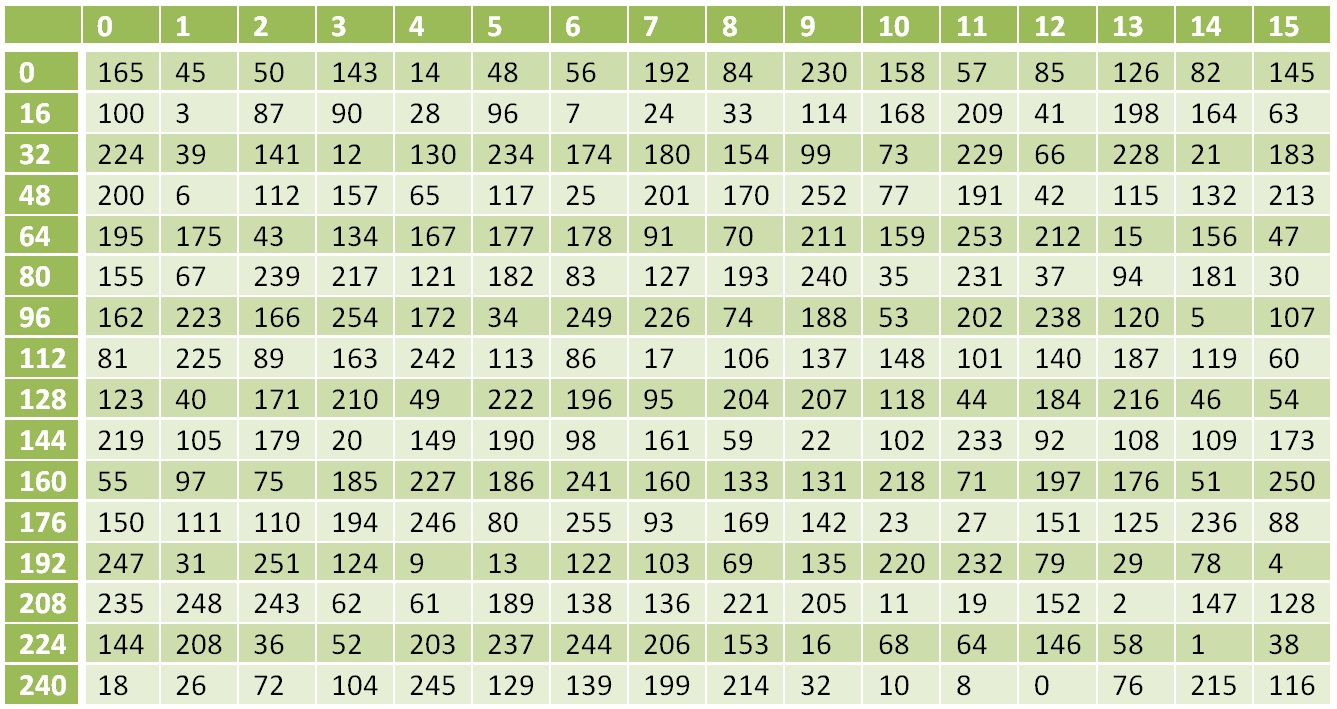عكس الجدول التحول غير الخطية

التحول العكسي إلى الدالة L سيكون:

$$

$$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$$

$$

$$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

والتحول في اتجاه المستوى الأعلى. (كرر العملية 16 مرة)

تنفيذ جافا

أولاً ، نحدد الثوابت اللازمة

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64]; 

لنقم بإنشاء جميع الوظائف الرئيسية:

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; } 

لتنفيذ الدالة L ، نحتاج إلى العديد من الوظائف المساعدة ، واحدة لحساب تكاثر الأرقام في حقل غالوا وواحد للتحول.

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; } 

وظائف عكسية:

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; } 

حسنا ، والوظيفة الرئيسية

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); } 

لقد تعلمنا تشفير كتلة البيانات من أجل تشفير النص الذي طوله أطول من طول الكتلة ؛ هناك العديد من الأوضاع الموضحة في المعيار - GOST 34.13-2015:

• وضع الاستبدال البسيط (Codebook Electronic، ECB) ؛
• وضع جاما (عداد ، نسبة النقر إلى الظهور) ؛
• وضع جاما مع ردود فعل الإخراج (ردود الفعل الإخراج ، OFB) ؛
• استبدال بسيط وضع تستعد (تشفير كتلة تسلسل ، CBC) ؛
• وضع جاما مع ردود الفعل في النص المشفر (ملاحظات التشفير ، CFB) ؛
• وضع رمز مصادقة الرسائل (MAC).

في جميع الأوضاع ، يجب أن يكون طول النص دائمًا مضاعفًا لطول الكتلة ، لذلك يتم دائمًا مبطن النص إلى اليمين ببت واحد واحد وأصفار إلى طول الكتلة.

أسهل وضع هو وضع الاستبدال البسيط. في هذا الوضع ، يتم تقسيم النص إلى كتل ، ثم يتم تشفير كل كتلة بشكل منفصل عن الباقي ، ثم يتم لصق كتل النص المشفر معًا ونحصل على رسالة مشفرة. هذا الوضع هو أبسط والأكثر ضعفا ويكاد لا يتم تطبيقه في الممارسة.

يمكن النظر في أوضاع أخرى بالتفصيل في وقت لاحق.